應用數據科學 (Applied data science)

Price and quantity are two fundamental measures that determine the bottom line of every business, and setting the right price is one of the most important decisions a company can make. Under-pricing hurts the company’s revenue if consumers are willing to pay more and, on the other hand, over-pricing can hurt in a similar fashion if consumers are less inclined to buy the product at a higher price.

價格和數量是確定每項業務底線的兩個基本指標，而設定正確的價格是公司可以做出的最重要決定之一。 如果消費者愿意支付更高的價格，定價過低會損害公司的收入；另一方面，如果消費者不太愿意以更高的價格購買產品，那么定價過高也會以類似的方式受到損害。

So given the tricky relationship between price and sales, where is the sweet spot — the optimum price — that maximizes product sales and earns most profit?

因此，考慮到價格與銷售之間的棘手關系，最佳產品的最佳銷售點在哪里？這可以最大化產品的銷售并獲得最大的利潤？

The purpose of this article is to answer this question by implementing a combination of the economic theory and a regression algorithm in Python environment.

本文的目的是通過在Python環境中實現經濟理論和回歸算法的結合來回答這個問題。

1.資料 (1. Data)

We are optimizing a future price based on the relationship between historical price and sales, so the first thing we need is the past data on these two indicators. For this exercise, I’m using a time series data on historical beef sales and corresponding unit prices.

我們正在根據歷史價格和銷售量之間的關系來優化未來價格，因此我們需要的第一件事是這兩個指標的過去數據。 在本練習中，我使用有關歷史牛肉銷售量和相應單價的時間序列數據。

# load data
import pandas as pd
beef = pd# view first few rows
beef.tail(5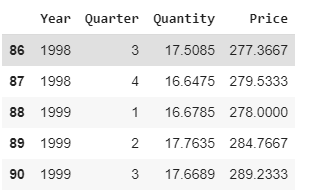

The dataset contains a total of 91 observations of quantity-price pairs reported on a quarterly basis.

該數據集包含每季度報告的91個數量-價格對的觀察值。

It is customary in data science to do exploratory data analysis (EDA), but I’m skipping that part to focus on modeling. Nevertheless, I strongly encourage taking this extra step to make sure you understand the data before building models.

數據科學中通常進行探索性數據分析(EDA)，但我跳過了這一部分，而只關注建模。 不過，我強烈建議您采取額外的步驟，以確保您在構建模型之前了解數據。

2.圖書館 (2. Libraries)

We need to import libraries for three reasons: manipulating data, building the model, and visualizing the functions.

我們需要導入庫的原因有三個：處理數據，構建模型和可視化功能。

We are importing numpy and pandas for creating and manipulating table, mtplotlib and seaborn for visualization and statsmodels API to build and run the regression model.

我們將導入numpy和pandas用于創建和操作表格， mtplotlib和seaborn用于可視化和statsmodels API以構建和運行回歸模型。

import numpy as np
from pandas import DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.formula.api import ols
%matplotlib inline

2.定義利潤函數 (2. Defining the profit function)

We know that revenue depends on the quantity sold and the unit price of products.

我們知道，收入取決于出售的數量和產品的單價。

We also know that profit is calculated by netting out costs from revenue.

我們也知道，利潤是通過從收入中扣除成本來計算的。

Putting these two together we get the following equations:

將這兩個放在一起，我們得到以下方程式：

# revenue
revenue = quantity * price # eq (1)# profit
profit = revenue - cost # eq (2)

We can rewrite the profit function by combining eq. #1 and 2 as follows:

我們可以結合等式來重寫利潤函數。 ＃1和2如下：

# revised profit function
profit = quantity * price - cost # eq (3)

Eq #3 tells us that we need three pieces of information to calculate profit: quantity, price and cost.

方程3告訴我們，我們需要三項信息來計算利潤：數量，價格和成本。

3.定義需求函數 (3. Defining the demand function)

We first need to establish the relationship between quantity and price — the demand function. This demand function is estimated from a “demand curve” based on the linear relationship between price and quantity.

我們首先需要建立數量和價格之間的關系-需求函數。 根據價格和數量之間的線性關系，根據“需求曲線”估算此需求函數。

# demand curve
sns.lmplot(x = "Price", y = "Quantity", 
data = beef, fig_reg = True, size = 4)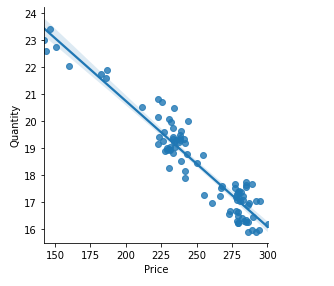

To find that demand curve we will fit an Ordinary Least Square (OLS) regression model.

為了找到需求曲線，我們將擬合普通最小二乘(OLS)回歸模型。

# fit OLS model
model = ols("Quantity ~ Price", data = beef).fit()# print model summary
print(model.summary())

The following are the regression results with the necessary coefficients needed for further analysis.

以下是回歸結果以及進一步分析所需的必要系數。

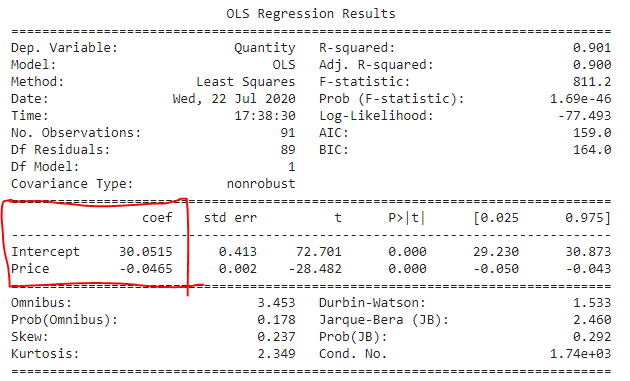
5.找到利潤最大化的價格 (5. Finding the profit-maximizing price)

The coefficient we are looking for is coming from the regression model above — the intercept and the price coefficient — to measure the corresponding sales quantity. We can now plug these values into equation 3.

我們正在尋找的系數來自上面的回歸模型(截距和價格系數)，用于測量相應的銷售量。 現在，我們可以將這些值插入方程式3。

# plugging regression coefficients
quantity = 30.05 - 0.0465 * price # eq (5)# the profit function in eq (3) becomes
profit = (30.05 - 0.0465 * price) * price - cost # eq (6)

The next step is to find the price we are looking for from a range of options. The codes below should be intuitive, but basically what we are doing here is calculating revenue for each price and the corresponding quantity sold.

下一步是從一系列選項中找到我們要尋找的價格。 下面的代碼應該很直觀，但是基本上我們在這里要做的是計算每個價格和相應銷售數量的收入。

# a range of diffferent prices to find the optimum one
Price = [320, 330, 340, 350, 360, 370, 380, 390]# assuming a fixed cost
cost = 80Revenue = []for i in Price:
   quantity_demanded = 30.05 - 0.0465 * i
   
   # profit function
   Revenue.append((i-cost) * quantity_demanded)# create data frame of price and revenue
profit = pd.DataFrame({"Price": Price, "Revenue": Revenue})#plot revenue against price
plt.plot(profit["Price"], profit["Revenue"])

If price and revenue are plotted, we can visually identify the peak of the revenue and find the price that makes the revenue at the highest point on the curve.

如果繪制了價格和收入，我們可以直觀地識別收入的峰值，并找到使收入處于曲線最高點的價格。

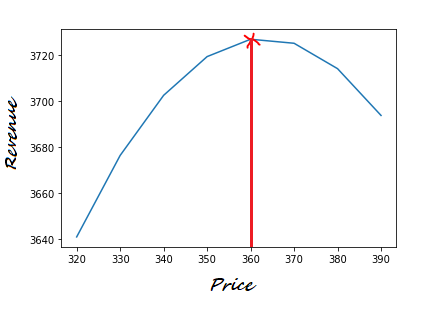
So we find that the maximum revenue at different price levels is reached at $3,726 when the price is set at $360.

因此，我們發現，當價格設為360美元時，在不同價格水平下的最高收入達到3,726美元。

# price at which revenue is maximum
profit[profit['Revenue'] == profit[['Revenue'].max()]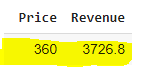

總結和結論 (Summary and conclusions)

The purpose of this article was to demonstrate how to find the price at which the revenue or profit is maximized using a combination of economic theory and statistical modeling. In the initial steps we defined the demand and profit functions, and then ran a regression to find the parameter values needed to feed into the profit/revenue function. And finally, we checked revenues under different price levels to get the price for the corresponding maximum revenue.

本文的目的是演示如何結合經濟理論和統計模型找到使收益或利潤最大化的價格。 在最初的步驟中，我們定義了需求和利潤函數，然后進行回歸以找到輸入利潤/收益函數所需的參數值。 最后，我們檢查了不同價格水平下的收入，以獲得對應的最大收入的價格。