BP神經網絡過程：

基本思想

BP算法是一個迭代算法，它的基本思想如下：

1. 將訓練集數據輸入到神經網絡的輸入層，經過隱藏層，最后達到輸出層并輸出結果，這就是前向傳播過程。
2. 由于神經網絡的輸出結果與實際結果有誤差，則計算估計值與實際值之間的誤差，并將該誤差從輸出層向隱藏層反向傳播，直至傳播到輸入層；
3. 在反向傳播的過程中，根據誤差調整各種參數的值（相連神經元的權重），使得總損失函數減小。
4. 迭代上述三個步驟（即對數據進行反復訓練），直到滿足停止準則。

梯度下降法

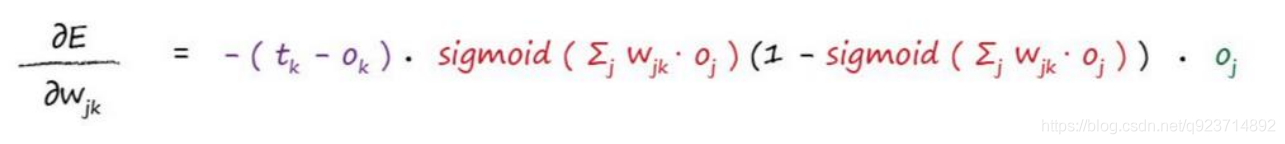
紫色部分：正確結果與節點輸出結果的差值，也就是誤差;
紅色部分：節點的激活函數，所有輸入該節點的鏈路把經過其上的信號與鏈路權重做乘積后加總，再把加總結果進行激活函數運算;
綠色部分：鏈路w(jk)前端節點輸出的信號值。

神經網絡訓練過程實例

1. 第一層是輸入層，包含兩個神經元：i1，i2 和偏置b1；
2. 第二層是隱藏層，包含兩個神經元：h1，h2 和偏置項b2；
3. 第三層是輸出：o1，o2。
4. 每條線上標的 wi 是層與層之間連接的權重。
5. 激活函數是 sigmod 函數。
6. 我們用 z 表示某神經元的加權輸入和；用 a 表示某神經元的輸出。
   

Step 1 前向傳播

輸入層 —> 隱藏層

隱藏層 —> 輸出層

Step 2 反向傳播

計算損失函數：

隱藏層 —> 輸出層的權值更新

輸入層 —> 隱藏層的權值更新

這樣，反向傳播算法就完成了，最后我們再把更新的權值重新計算，不停地迭代。 在這個例子中第一次迭代之后，總誤差0.298371109下降至0.291027924。
迭代10000次后，總誤差為0.000035085。輸出為：[0.015912196, 0.984065734]