梯度下降算法是一個很基本的算法，在機器學習和優化中有著非常重要的作用，本文首先介紹了梯度下降的基本概念，然后使用python實現了一個基本的梯度下降算法。梯度下降有很多的變種，本文只介紹最基礎的梯度下降，也就是批梯度下降。

---

實際應用例子就不詳細說了，網上關于梯度下降的應用例子很多，最多的就是NG課上的預測房價例子：?
假設有一個房屋銷售的數據如下：

面積(m^2) 銷售價錢（萬元）

面積(m^2)	銷售價錢（萬元）
123	250
150	320
87	180

根據上面的房價我們可以做這樣一個圖：

于是我們的目標就是去擬合這個圖，使得新的樣本數據進來以后我們可以方便進行預測：?

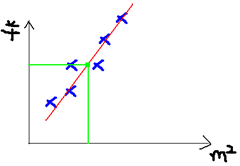
對于最基本的線性回歸問題，公式如下：?
?
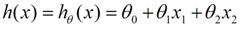x是自變量，比如說房子面積。θ是權重參數，也就是我們需要去梯度下降求解的具體值。

在這兒，我們需要引入損失函數（Loss function 或者叫 cost function），目的是為了在梯度下降時用來衡量我們更新后的參數是否是向著正確的方向前進，如圖損失函數（m表示訓練集樣本數量）：?
?
下圖直觀顯示了我們梯度下降的方向，就是希望從最高處一直下降到最低出：?

梯度下降更新權重參數的過程中我們需要對損失函數求偏導數：?
?
求完偏導數以后就可以進行參數更新了：?
?
偽代碼如圖所示：?

好了，下面到了代碼實現環節，我們用Python來實現一個梯度下降算法，求解:

，也就是求解: 中的a，b，c三個參數 。

下面是代碼：

import numpy as np
import matplotlib.pyplot as plt
#y=2 * (x1) + (x2) + 3 
rate = 0.001
x_train = np.array([    [1, 2],    [2, 1],    [2, 3],    [3, 5],    [1, 3],    [4, 2],    [7, 3],    [4, 5],    [11, 3],    [8, 7]    ])
y_train = np.array([7, 8, 10, 14, 8, 13, 20, 16, 28, 26])
x_test  = np.array([    [1, 4],    [2, 2],    [2, 5],    [5, 3],    [1, 5],    [4, 1]    ])a = np.random.normal()
b = np.random.normal()
c = np.random.normal()def h(x):return a*x[0]+b*x[1]+cfor i in range(10000):sum_a=0sum_b=0sum_c=0for x, y in zip(x_train, y_train):sum_a = sum_a + rate*(y-h(x))*x[0]sum_b = sum_b + rate*(y-h(x))*x[1]sum_c = sum_c + rate*(y-h(x))a = a + sum_ab = b + sum_bc = c + sum_cplt.plot([h(xi) for xi in x_test])print(a)
print(b)
print(c)result=[h(xi) for xi in x_train]
print(result)result=[h(xi) for xi in x_test]
print(result)plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

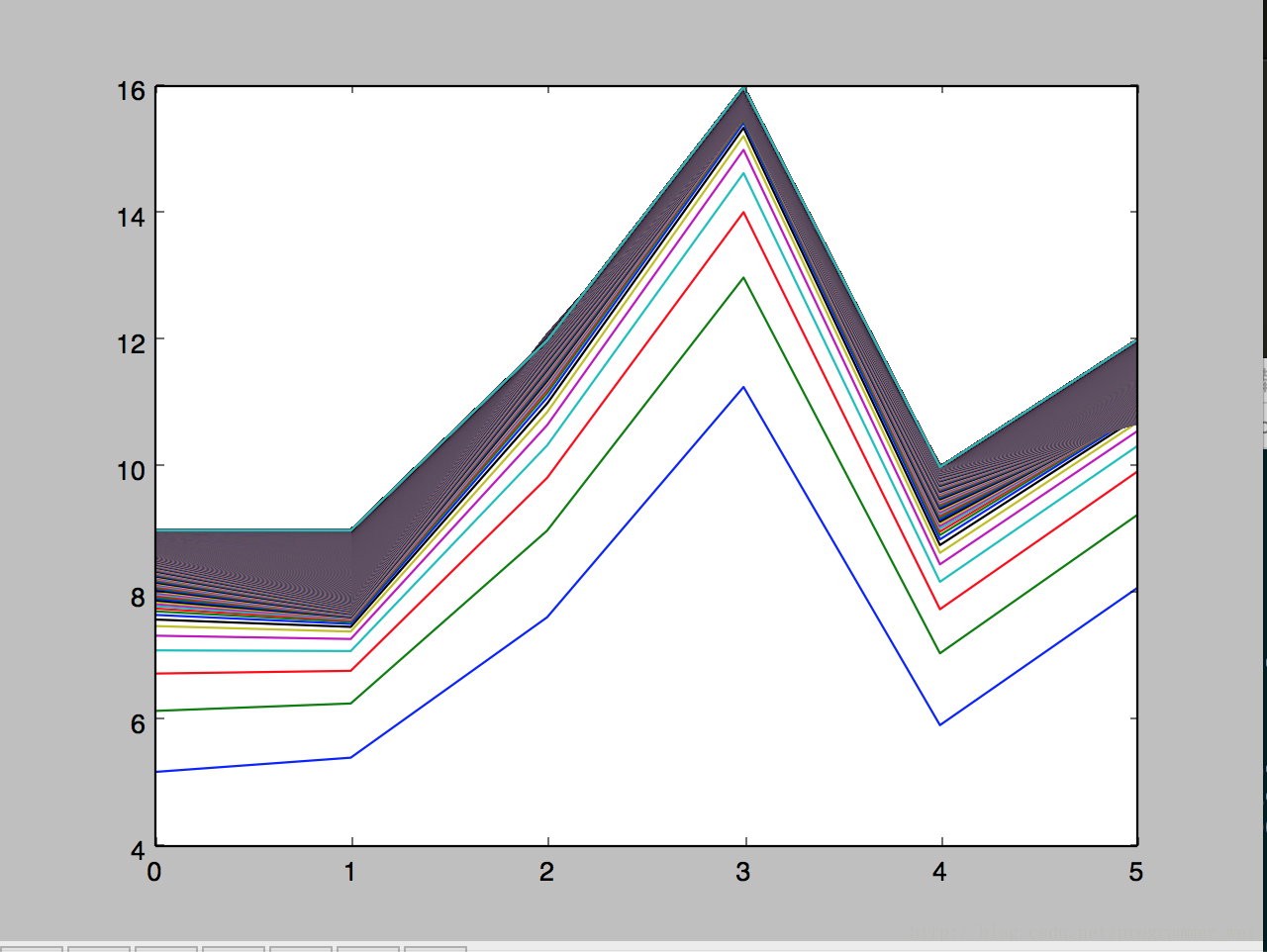
x_train是訓練集x，y_train是訓練集y， x_test是測試集x，運行后得到如下的圖，圖片顯示了算法對于測試集y的預測在每一輪迭代中是如何變化的：?

我們可以看到，線段是在逐漸逼近的，訓練數據越多，迭代次數越多就越逼近真實值。