組合

題目描述

給定兩個整數 n 和 k，返回范圍 [1, n] 中所有可能的 k 個數的組合。

你可以按 任何順序 返回答案。

示例 1：
輸入：n = 4, k = 2 輸出： [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4] ]

示例 2：
輸入：n = 1, k = 1 輸出：[ [1] ]

提示：
1 <= n <= 20
1 <= k <= n

思路構建

本題直接的解法當然是利用for循環暴力搜索，例如 k=2時，用兩個for循環就能得到結果,如下所示：

int n = 4;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {cout << i << " " << j << endl;}
}

但一旦當k變得很大時就必須嵌套很多for循環，這顯然是不顯示的，而回溯法就用遞歸來解決嵌套層數的問題。

為了方便理解，我們可以將遞歸過程轉化為一個樹結構，如下所示：?

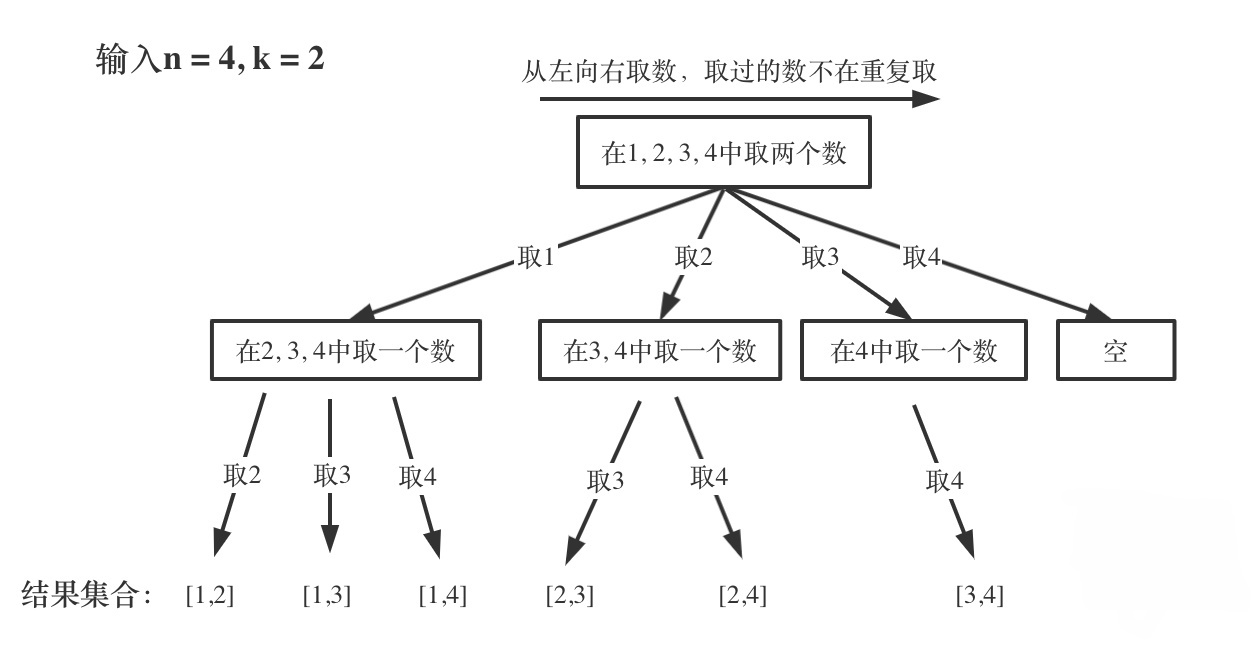
每次從集合中選取元素，可選擇的范圍隨著選擇的進行而收縮，調整可選擇的范圍。
圖中可以發現n相當于樹的寬度，k相當于樹的深度。
圖中每次搜索到了葉子節點，我們就找到了一個結果。

解題步驟

按照回溯三部曲的模板套路來進行：

1.遞歸函數的返回值以及參數
定義兩個全局變量，一個用來存放符合條件單一結果，一個用來存放符合條件結果的集合。

vector<vector<int>> result; // 存放符合條件結果的集合
vector<int> path; // 用來存放符合條件結果

然后還需要一個參數，為int型變量startIndex，這個參數用來記錄本層遞歸的中，集合從哪里開始遍歷（集合就是[1,...,n] ）。

startIndex 可以防止出現重復的組合。

vector<vector<int>> result; // 存放符合條件結果的集合
vector<int> path; // 用來存放符合條件單一結果
void backtracking(int n, int k, int startIndex)

2.回溯函數終止條件
path這個數組的大小如果達到k，說明我們找到了一個子集大小為k的組合了，在圖中path存的就是根節點到葉子節點的路徑。

此時用result二維數組，把path保存起來，并終止本層遞歸。

if (path.size() == k) {result.push_back(path);return;
}

3.單層搜索的過程
回溯法的搜索過程就是一個樹型結構的遍歷過程，可以看出for循環用來橫向遍歷，遞歸的過程是縱向遍歷。

for循環每次從startIndex開始遍歷，然后用path保存取到的節點i。

for (int i = startIndex; i <= n; i++) { // 控制樹的橫向遍歷path.push_back(i); // 處理節點backtracking(n, k, i + 1); // 遞歸：控制樹的縱向遍歷，注意下一層搜索要從i+1開始path.pop_back(); // 回溯，撤銷處理的節點
}

可以看出backtracking（遞歸函數）通過不斷調用自己一直往深處遍歷，總會遇到葉子節點，遇到了葉子節點就要返回。

backtracking的下面部分就是回溯的操作了，撤銷本次處理的結果。

執行過程示例

為了方便理解遞歸過程，以 n=4, k=2 為例，一步步拆解遞歸流程

第一層遞歸（startIndex=1，需選第 1 個元素）

for (i=1; i<=4; i++) {i=1：path.push_back(1) → path = [1]遞歸調用 backtracking(4, 2, 2)  // 下一層從 2 開始，選第 2 個元素（遞歸返回后）path.pop_back() → path = []i=2：path.push_back(2) → path = [2]遞歸調用 backtracking(4, 2, 3)（返回后）path.pop_back() → path = []i=3：path.push_back(3) → path = [3]遞歸調用 backtracking(4, 2, 4)（返回后）path.pop_back() → path = []i=4：path.push_back(4) → path = [4]遞歸調用 backtracking(4, 2, 5)（返回后）path.pop_back() → path = []
}

第二層遞歸（startIndex=2，需選第 2 個元素）

// 此時 path = [1]，需選第 2 個元素，startIndex=2
for (i=2; i<=4; i++) {i=2：path.push_back(2) → path = [1,2]（長度=k=2，加入結果集）遞歸終止，返回上層path.pop_back() → path = [1]i=3：path.push_back(3) → path = [1,3]（加入結果集）返回上層，path.pop_back() → path = [1]i=4：path.push_back(4) → path = [1,4]（加入結果集）返回上層，path.pop_back() → path = [1]
}

通過上述流程，最終會生成所有符合條件的組合：[1,2], [1,3], [1,4], [2,3], [2,4], [3,4]。

C++ 代碼實現

class Solution {
private:vector<vector<int>> result; // 存放符合條件結果的集合vector<int> path; // 用來存放符合條件結果void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 處理節點backtracking(n, k, i + 1); // 遞歸path.pop_back(); // 回溯，撤銷處理的節點}}
public:vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return result;}
};

復雜度分析

時間復雜度: O(n * 2^n)
空間復雜度: O(n)

剪枝優化

原代碼的 for 循環遍歷范圍是 i = startIndex 到 i <= n，但部分循環是無效的（剩余元素不足以選夠 k 個），可通過剪枝減少不必要的迭代。

剪枝原理
假設當前 path 中已有 m 個元素（m = path.size()），還需要選擇 k - m 個元素。 剩余可選元素從 i 到 n，共 n - i + 1 個元素。 為了能選夠 k - m 個元素，需滿足：n - i + 1 >= k - m → 變形得 i <= n - (k - m) + 1。

若 i 超過這個值，即使選擇 i，剩余元素也不夠，無需繼續循環。

來舉一個例子，n = 4，k = 4的話，那么第一層for循環的時候，從元素2開始的遍歷都沒有意義了，如下圖所示：?

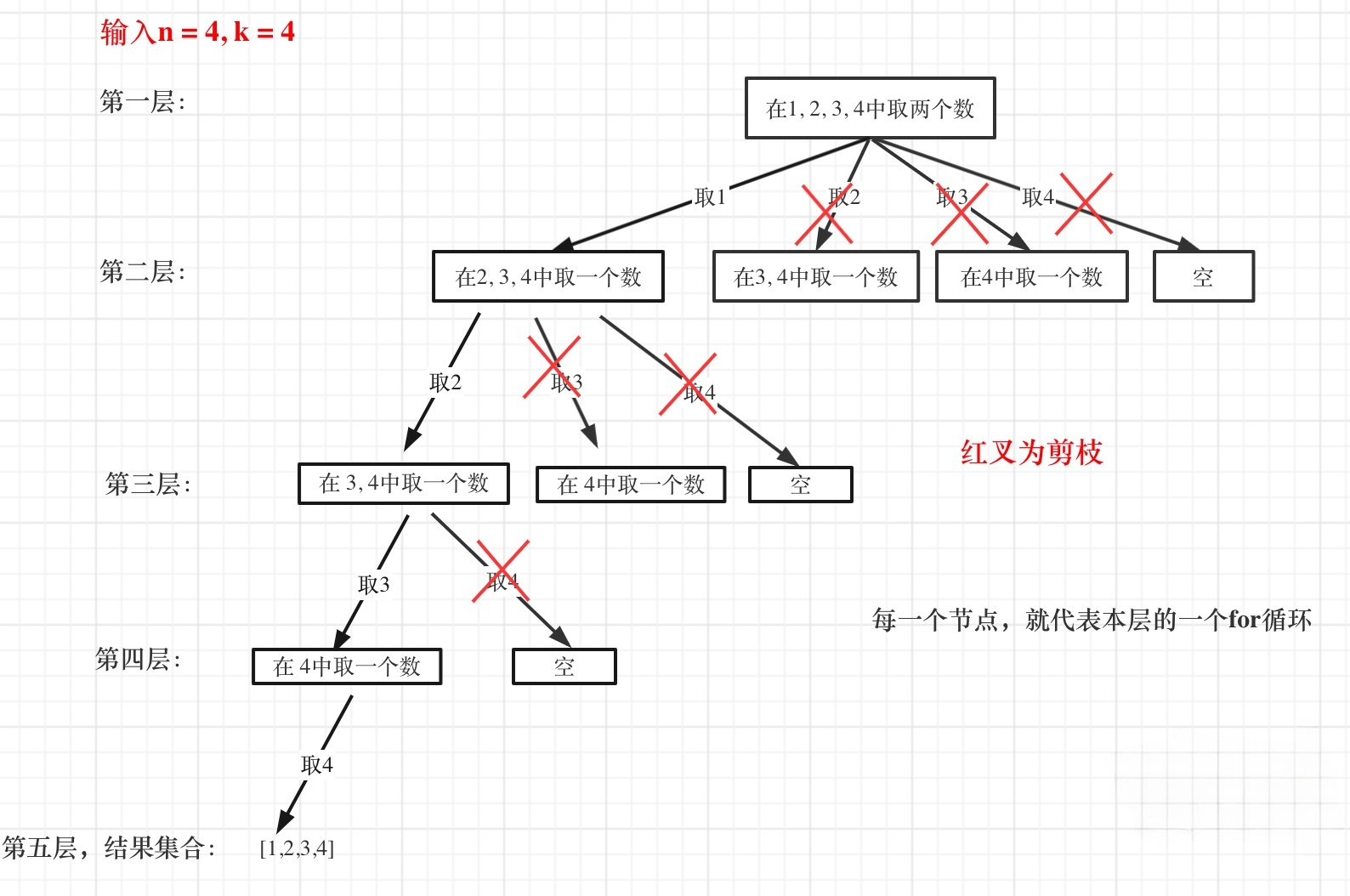
所以，可以剪枝的地方就在遞歸中每一層的for循環所選擇的起始位置。

如果for循環選擇的起始位置之后的元素個數 已經不足 我們需要的元素個數了，那么就沒有必要搜索了。

優化過程

• 已經選擇的元素個數：path.size();

• 還需要的元素個數為: k - path.size();

• 在集合n中至多要從該起始位置 : n - (k - path.size()) + 1，開始遍歷

為什么有個+1呢，因為包括起始位置，我們要是一個左閉的集合。

舉個例子，n = 4，k = 3， 目前已經選取的元素為0（path.size為0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

所以優化之后的for循環是

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i為本次搜索的起始位置