暑期算法訓練.13

57 力扣14最長公共前綴

57.1 題目解析：

57.2 算法思路

57.3 代碼演示：

?編輯?

57.4 總結反思：

58 力扣 5最長回文字符串

58.1 題目解析：

?編輯?

58.2 算法思路：

58.3 代碼演示：

?編輯

58.4 總結反思：

59 力扣模擬二進制之和

59.1 題目解析：

59.2 算法思路：

59.3 代碼演示：

?編輯

59.4 總結反思

60. 力扣43 字符串相乘

60.1 題目解析：

60.2 算法思路:

60.3 代碼演示：

60.4 總結反思

57 力扣14最長公共前綴

57.1 題目解析：

這道題目的題意很好理解吧。就是找這些字符串的最長的公共前綴即可

57.2 算法思路

?那么這道題目有幾種解法。

解法一：解法一就是兩兩比較去找出公共前綴

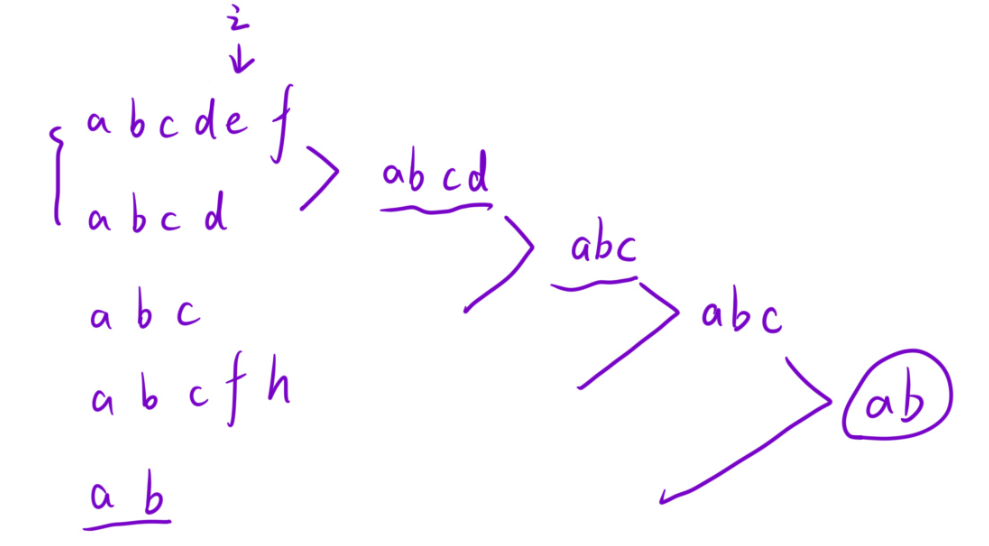
那么這種解法就是兩兩的進行比較即可。那么此時的時間復雜度是O（m*n），m是字符串的個數，n是每一個字符串的長度（假設是相等的每一個字符串的長度）。

那么咱們再來看一個解法，就是解法二：

統一比較：

那么此時會出現兩種情況得讓i停止，咱們都得考慮到。

咱們這個的處理方法是先讓i小于第一個字符串的長度，然后再定義一個j去豎著遍歷，類似于二維數組，則i<str.size(),j小于strs的長度（即字符串的個數），然后strs[j][i]。就是第j行i列

57.3 代碼演示：

咱們先來看一下解法一就是兩兩比較的：

?

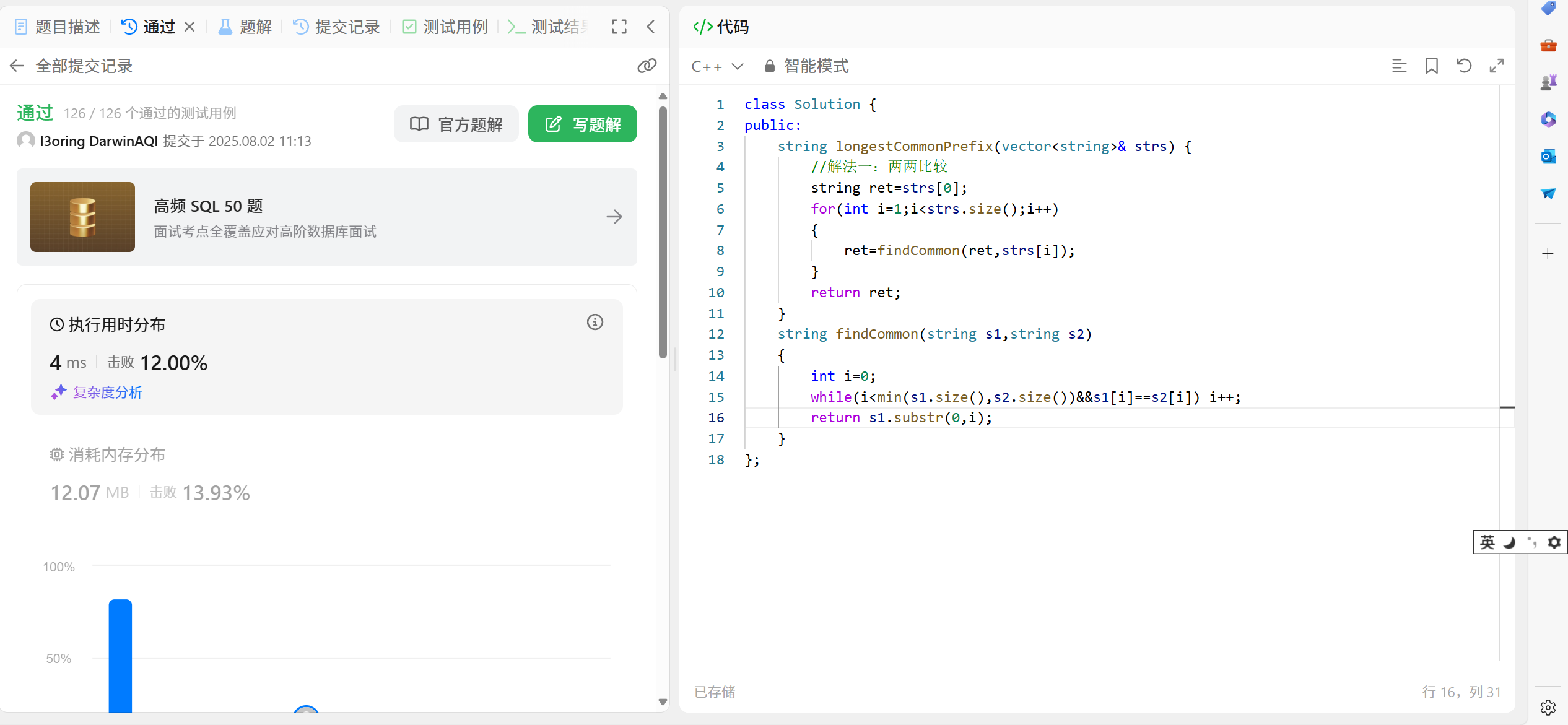string findCommon(string s1, string s2);
string longestCommonPrefix(vector<string>& strs) {//解法一：兩兩比較string ret = strs[0];for (int i = 1; i < strs.size(); i++){ret = findCommon(ret, strs[i]);}return ret;
}
string findCommon(string s1, string s2)
{int i = 0;while (i < min(s1.size(), s2.size()) && s1[i] == s2[i]) i++;return s1.substr(0, i);
}
int main()
{vector<string> strs = { "flower","flow","flight" };cout << longestCommonPrefix(strs) << endl;return 0;
}

解法二：

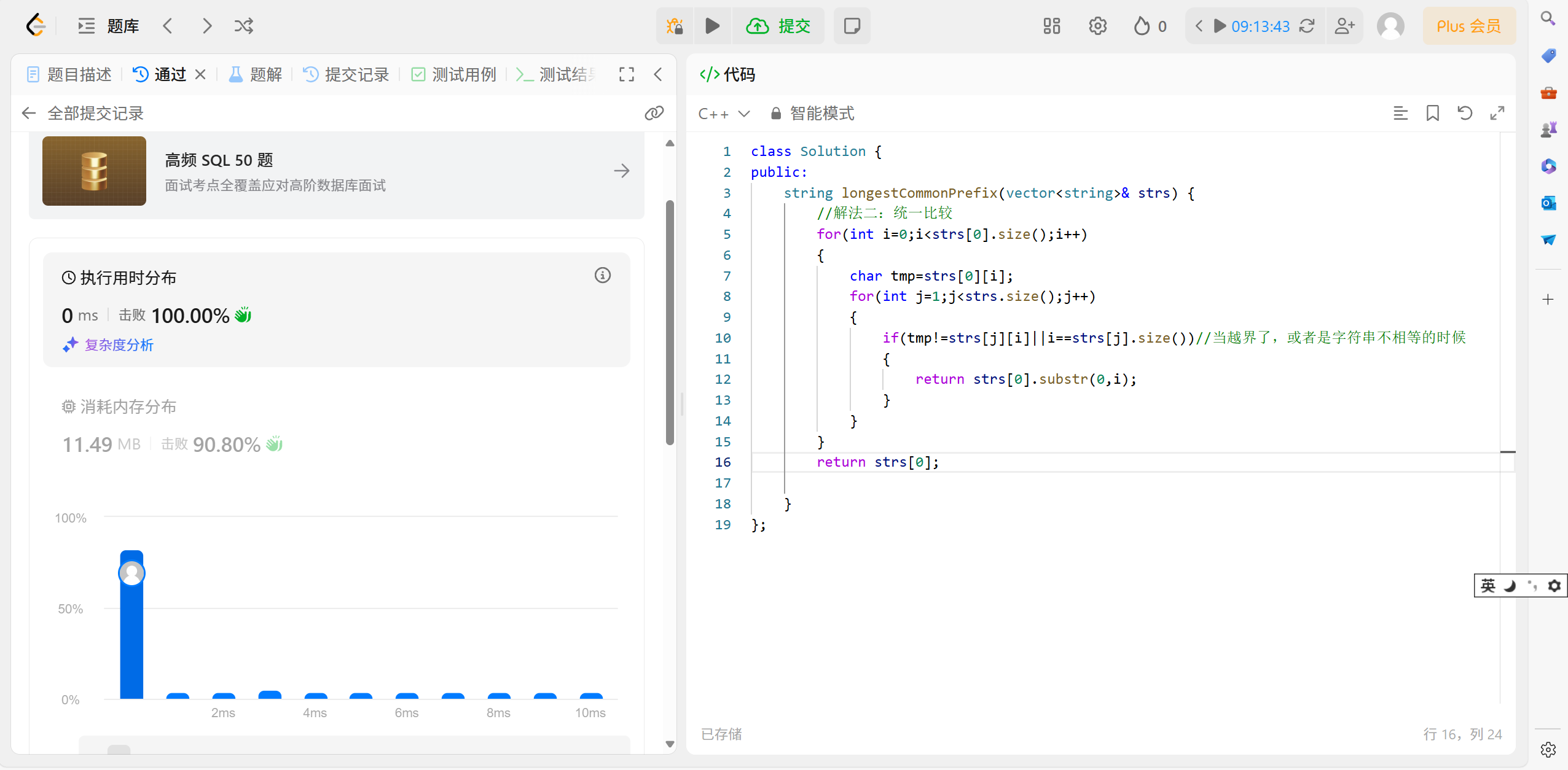
string longestCommonPrefix(vector<string>& strs) {//解法二：統一比較for (int i = 0; i < strs[0].size(); i++){char tmp = strs[0][i];for (int j = 1; j < strs.size(); j++){if (tmp != strs[j][i] || i == strs[j].size())//當越界了，或者是字符串不相等的時候{return strs[0].substr(0, i);}}}return strs[0];
}
int main()
{vector<string> strs = { "flower","flow","flight" };cout << longestCommonPrefix(strs) << endl;return 0;
}

57.4 總結反思：

其實字符串類型的題目不只是字符串，還有其他相關的知識。比如模擬，等等

58 力扣 5最長回文字符串

58.1 題目解析：

?

題目很清晰，就是讓你找到最長的回文子串

58.2 算法思路：

咱們可以使用中心擴展算法來做這道題目

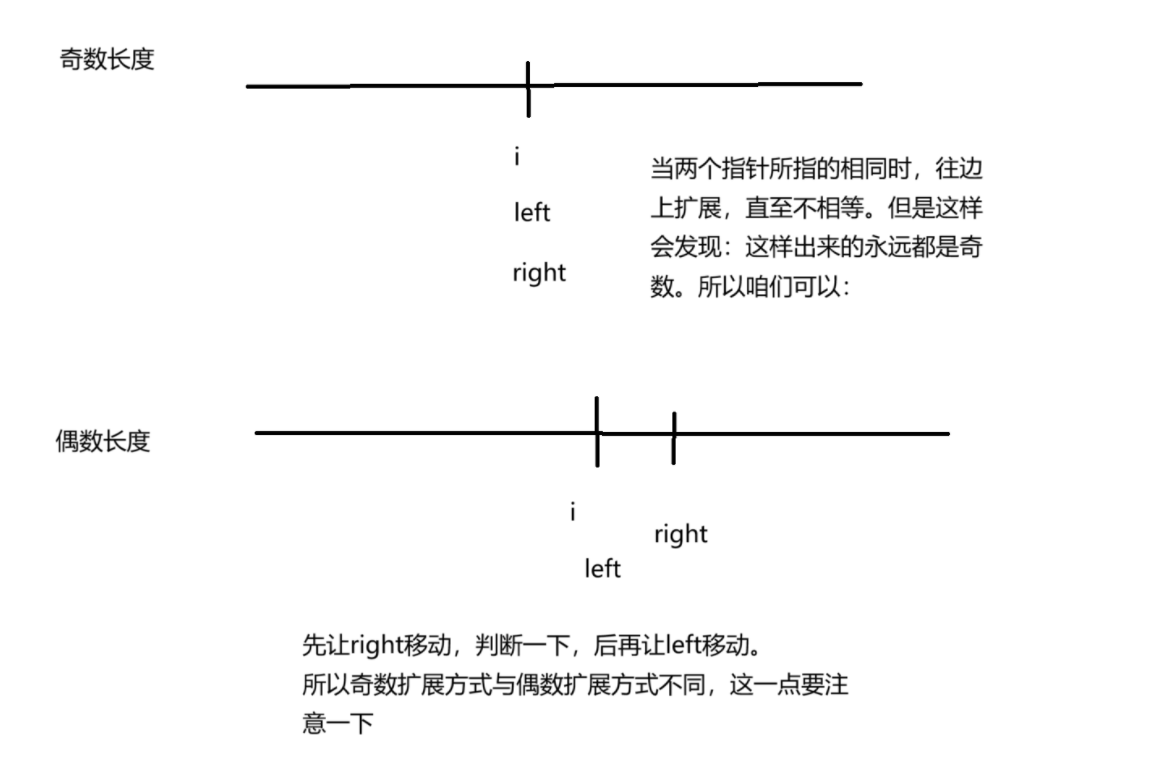
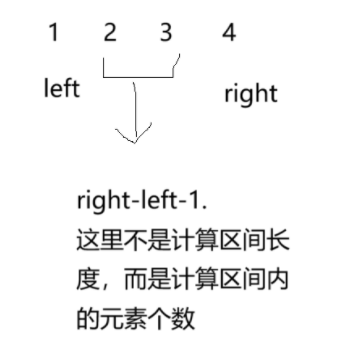最后返回的是這個字符串的left與right之間的元素個數。所以，可用substr(......)

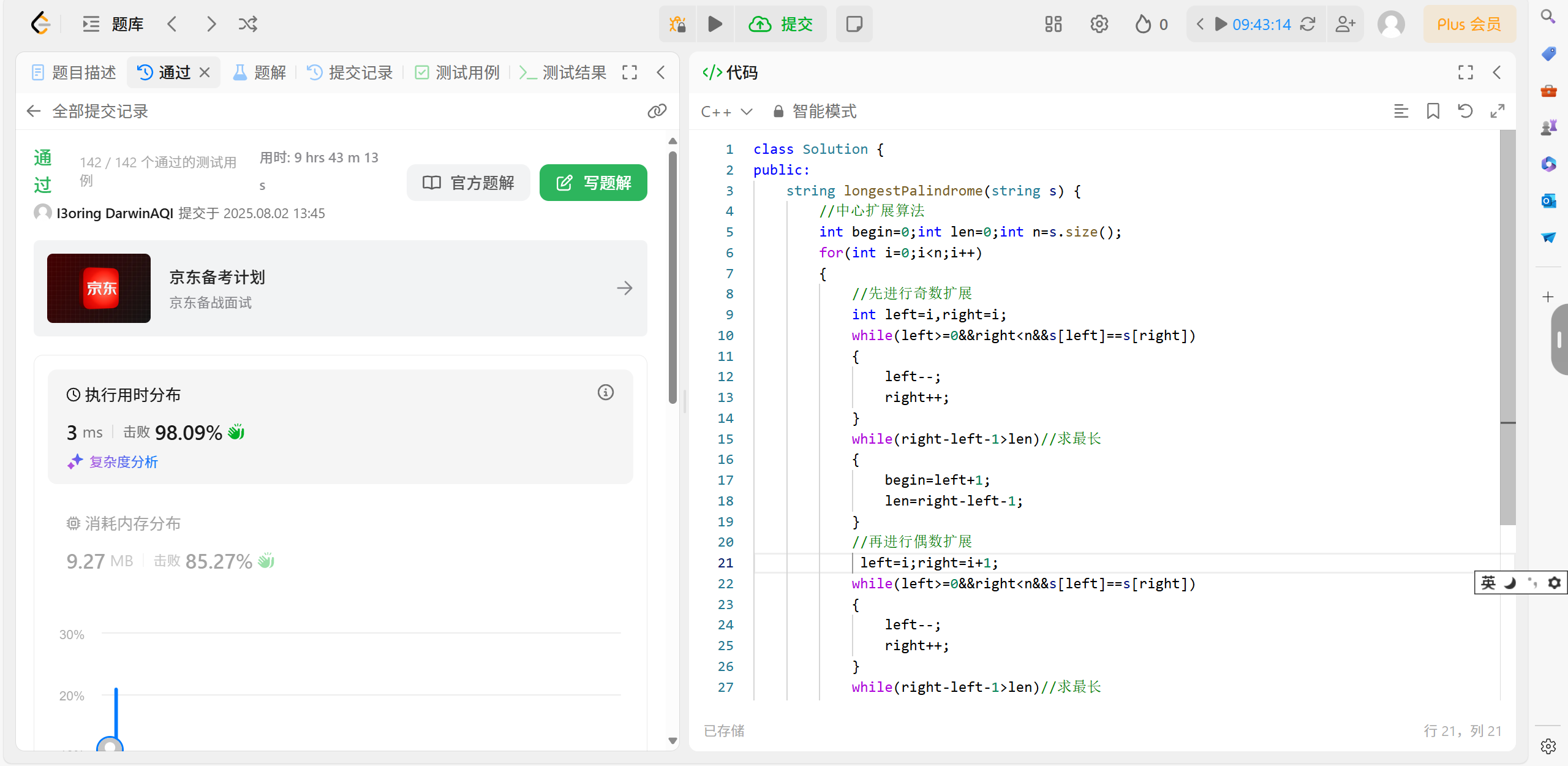
58.3 代碼演示：

string longestPalindrome(string s) {//中心擴展算法int begin = 0; int len = 0; int n = s.size();for (int i = 0; i < n; i++){//先進行奇數擴展int left = i, right = i;while (left >= 0 && right < n && s[left] == s[right]){left--;right++;}while (right - left - 1 > len)//求最長{begin = left + 1;len = right - left - 1;}//再進行偶數擴展left = i; right = i + 1;while (left >= 0 && right < n && s[left] == s[right]){left--;right++;}while (right - left - 1 > len)//求最長{begin = left + 1;len = right - left - 1;}}return s.substr(begin, len);
}
int main()
{string s("babad");cout << longestPalindrome(s) << endl;return 0;
}

58.4 總結反思：

這道題目其實使用其他的方法也是可以去做的

59 力扣模擬二進制之和

59.1 題目解析：

就是讓你模擬如何進行二進制的相加，別忘了進位即可

59.2 算法思路：

大家看這個題，是不是跟那個兩數之和（之前咱們使用鏈表做的那個題很像？）沒錯，就是一樣的思路：

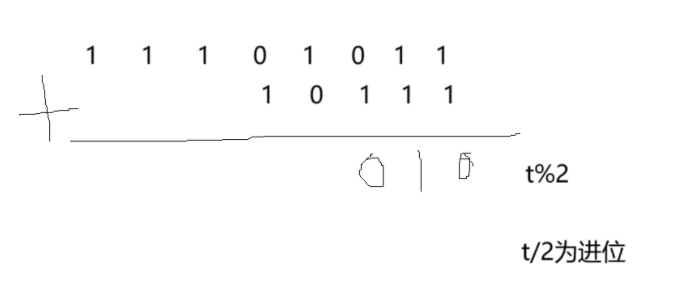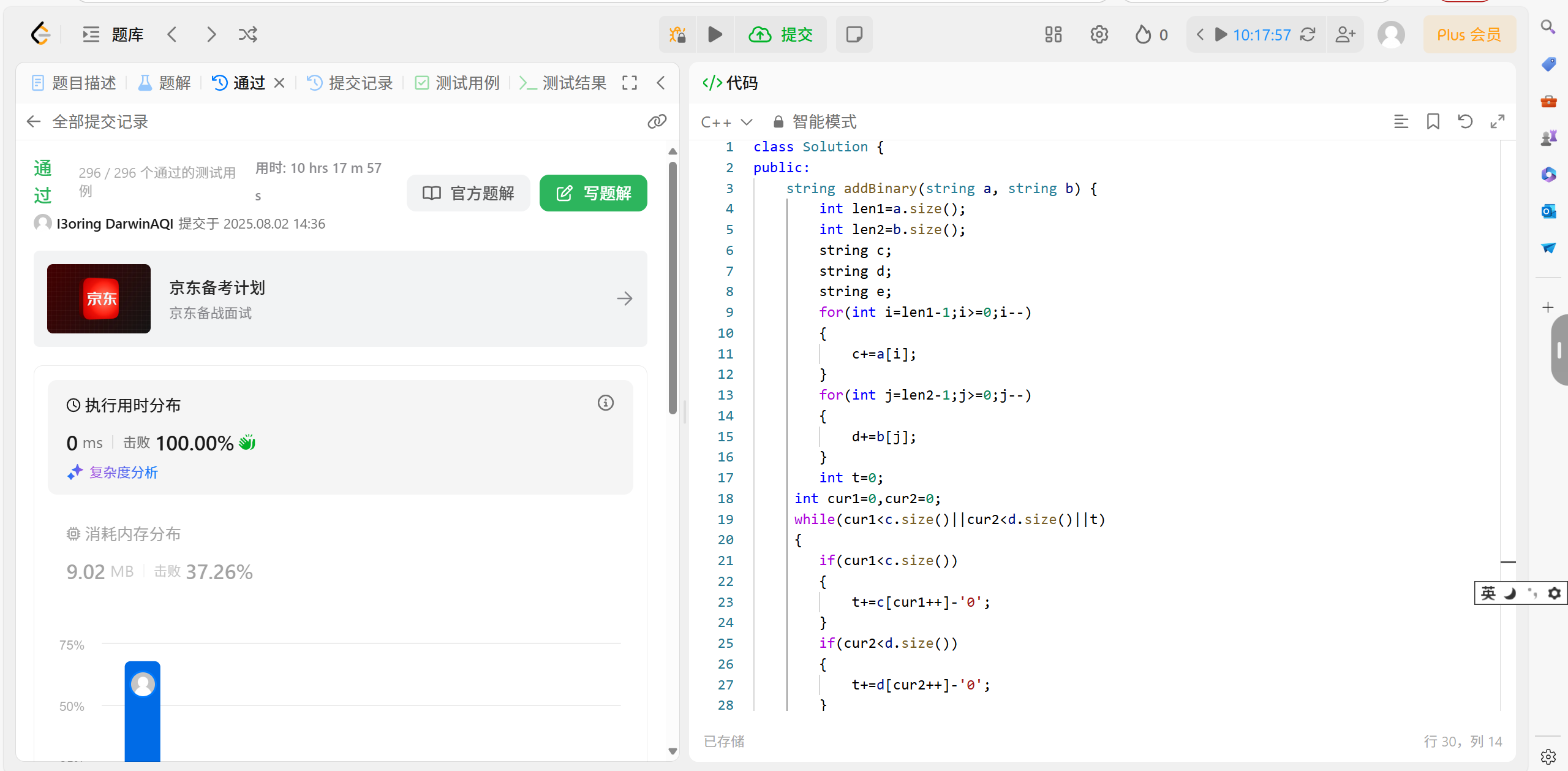
59.3 代碼演示：

string addBinary(string a, string b) {int len1 = a.size();int len2 = b.size();string c;string d;string e;for (int i = len1 - 1; i >= 0; i--){c += a[i];}for (int j = len2 - 1; j >= 0; j--){d += b[j];}int t = 0;int cur1 = 0, cur2 = 0;while (cur1 < c.size() || cur2 < d.size() || t){if (cur1 < c.size()){t += c[cur1++] - '0';//字符轉數字，字符串里面的全都是字符}if (cur2 < d.size()){t += d[cur2++] - '0';}e += t % 2 + '0';//數字轉字符t /= 2;}reverse(e.begin(), e.end());return e;
}
int main()
{string a("1010");string b("1011");cout << addBinary(a, b) << endl;return 0;
}

這道題目咱們還是需要逆序一下子的，不過博主一開始的逆序方式挺智障的hhh，明明可以用reverse來逆序

59.4 總結反思

這道題目其實還可以，下面這一道題目才是王炸

60. 力扣43 字符串相乘

60.1 題目解析：

這道題目很好理解，但是不是很好做。我依稀記得，這道題目是我一開始學C++語法，剛學了一點，就開始做這道題目，當時，這道題目我做了6個小時，沒錯，你沒看錯，6個小時，不斷地調試調試，可算是把那幾個邊界條件給調試了出來。但是我今天再去學習的時候，就發現了另外一種的優化方案。

60.2 算法思路:

?那么方法一就是普通的算式：

1. addStrings 函數：實現兩個字符串表示的非負整數的相加。
思路：從兩個字符串的末尾（個位）開始逐位相加，模擬豎式加法，注意進位。
具體步驟：
- 初始化：i 和 j 分別指向 num1 和 num2 的最后一個字符，index（表示進位）初始為0。
- 循環條件：當 i >= 0 或 j >= 0 時，說明還有數字沒有加完。
- 在循環內：
ret = 0;
如果 i >= 0，則將 num1[i] 轉換為數字并加到 ret 上，然后 i--。
如果 j >= 0，則將 num2[j] 轉換為數字并加到 ret 上，然后 j--。
如果進位 index > 0（注意這里index是上一位的進位，初始為0，但每次進位后會被重置，所以每次循環最多只會有一次進位加入），將進位加到 ret 上，并把 index 置0。
判斷 ret 是否 >= 10，如果是，則計算新的進位 index = ret / 10（實際上就是1，因為兩個一位數相加最大18，所以進位只能是1，但這里用除法更通用），然后 ret %= 10。
將 ret 轉換為字符，添加到結果字符串 ans 中。
- 循環結束后，如果還有進位（index > 0），則在結果后面添加一個'1'（因為進位最多為1）。
- 由于我們是從個位開始加，結果字符串是逆序的，所以最后需要反轉整個字符串。
2. multiply 函數：使用加法模擬乘法。
思路：模擬豎式乘法，將乘數的每一位與被乘數相乘，然后累加，注意乘數每一位的權重（后面要補零）。
具體步驟：
- 如果其中一個數為"0"，則直接返回"0"。
- 初始化 ans 為空字符串。
- 從 num1 的個位開始（即從后往前）遍歷每一位：
用當前位數字（記為ret）乘以 num2，這里通過連續調用 addStrings 函數來實現：用 while 循環，將 num2 累加 ret 次（注意：ret是數字，比如'5'，則累加5次）。得到的結果就是當前位與num2的乘積（字符串形式）。
然后把這個乘積加到最終結果 ans 上（用addStrings）。
將 num2 后面添加一個'0'（相當于乘以10），因為下一位是十位，所以被乘數需要擴大10倍（在豎式中，我們通常向左移位）。

解法二就是優化，即無進位相乘然后相加，最后再處理進位

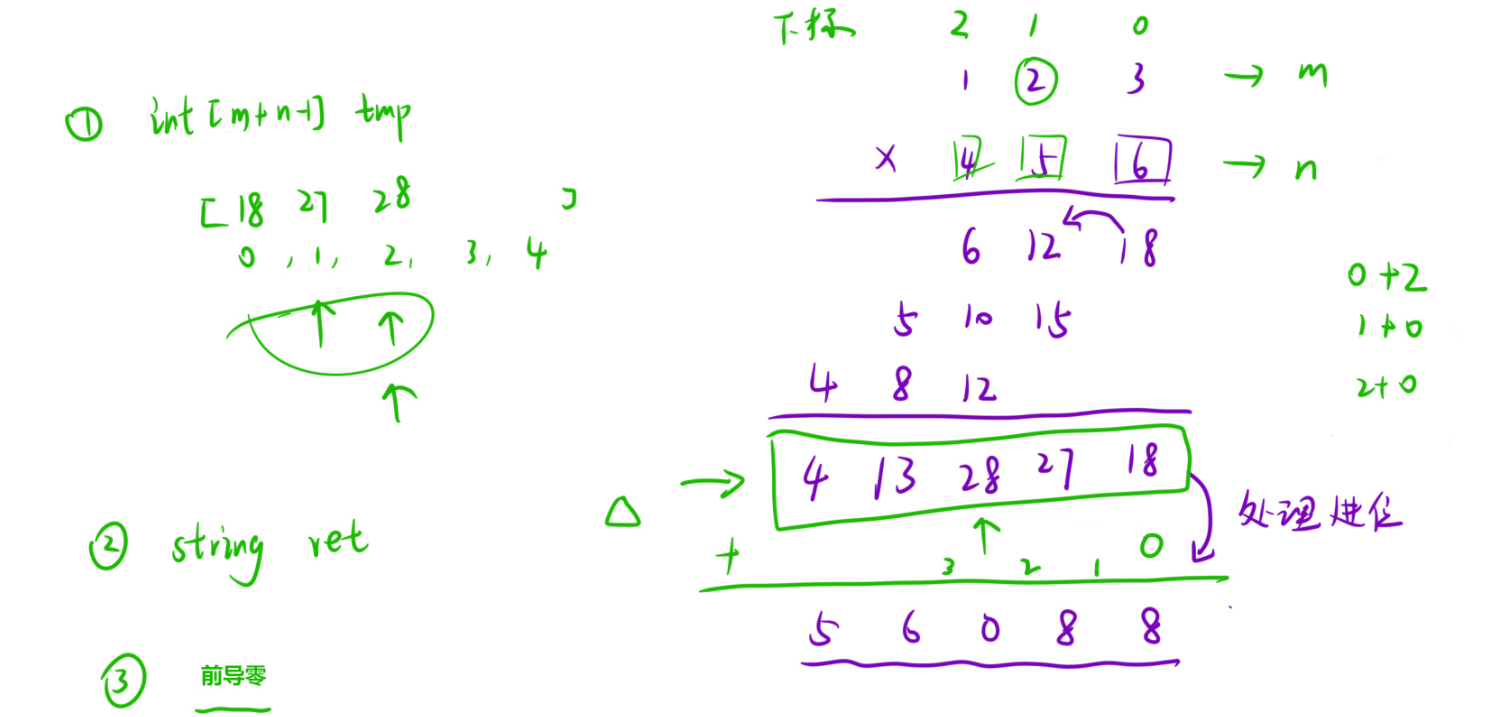模擬豎式乘法的另一種方式，先忽略進位，將每一位相乘的結果累加到一個臨時數組中，然后統一處理進位。
具體步驟：
- 首先反轉兩個字符串，使得從低位到高位排列（即下標0對應個位）。
- 創建一個臨時數組 tmp，大小為 m + n - 1（兩個數相乘，結果位數最多為m + n，最少為m + n - 1，這里先按最少分配，后面進位可能會增加位數）。
- 第一步：無進位相乘后相加。
遍歷 num1 的每一位（反轉后）和 num2 的每一位，將相乘的結果加到 tmp 數組的對應位置（tmp[i + j]）上。
注意：這里 i 和 j 分別從0開始，所以 i + j 就是兩個數位相乘結果應該放的位數（個位乘個位放在0號位置，十位乘個位放在1號位置，以此類推）。
- 第二步：處理進位。
初始化 cur = 0（當前處理的位置），t = 0（進位），以及結果字符串 ret。
循環條件：cur 小于 m + n - 1（即還有位數未處理）或者 t 不為0（還有進位未處理完）。
在循環內：
如果 cur 還在數組范圍內，則取出當前位的值加到 t 上，然后 cur++。
將 t 的個位（t % 10）轉換為字符加到 ret 的末尾。
將 t 除以10（得到進位），繼續下一位。
- 第三步：處理前導零。
????????由于我們是從低位到高位處理，所以結果字符串是逆序的（個位在最前面，最高位在最后面），而且可能有前導零（比如最后幾位進位后可能變成0，但我們處理進位時已經將進位處理完，所以最后幾位可能是0，但實際結果中不應該有前導零）。
????????注意：在反轉之前，我們的字符串是低位在前，所以最后連續的0在字符串的尾部（在反轉后會變成前導零）。但是我們在處理進位時，最后可能多出進位，所以字符串長度可能大于實際位數。不過，在第二步中，我們處理進位時已經將所有的位數都處理了，包括進位，所以最后得到的字符串應該是正確的，但是可能有前導零（在反轉后變成前導零，但此時我們還沒有反轉）。
????????然而，在第二步中，我們是從低位到高位處理，得到的結果字符串也是低位在前。在反轉之前，我們需要去掉字符串末尾的0（因為反轉后這些0會變成前導零）。但是注意：如果結果就是0，那么我們應該保留一個0。
????????所以，循環：當 ret 的長度大于1且最后一個字符是'0'時，刪除最后一個字符（即反轉前，我們刪除字符串尾部的0，這些0在反轉后會變成前導零）。
- 反轉字符串，得到最終結果。?

好，那么咱們可以推導出方法一的效率低（大數字時性能差）?。但是方法二的效率高（適合大數運算）。

60.3 代碼演示：

方法一：

//方法一：
string addStrings(string num1, string num2) {string ans; // 存儲結果int index = 0;// 進位，初始為0int i = num1.size() - 1;// 從num1的個位開始int j = num2.size() - 1;// 從num2的個位開始while (i >= 0 || j >= 0) {int ret = 0;if (i >= 0)ret += num1[i] - '0';// 取num1當前位數字if (j >= 0)ret += num2[j] - '0';// 取num2當前位數字if (index > 0) { // 如果有進位，則加上進位ret += index;index = 0; // 進位已經加入，清零}if (ret >= 10) {// 如果相加結果大于等于10，需要進位index = ret / 10;// 計算進位（這里ret最多19，所以進位為1，但寫法通用）ret %= 10; // 取余數}ans.push_back('0' + ret);// 將當前位的數字轉為字符，加入結果j--;// 移動指針i--;}if (index > 0) // 如果最后還有進位ans.push_back('1');// 在結果末尾加上進位1（因為進位最多為1）reverse(ans.begin(), ans.end()); // 反轉字符串return ans;
}
string multiply(string num1, string num2) {if (num1 == "0" || num2 == "0")// 處理乘數為0的情況return "0";string ans;for (int i = num1.size() - 1; i >= 0; i--) {// 從num1的個位開始string str;// 用來存儲當前位乘以num2的結果int ret = num1[i] - '0'; // 當前位的數字while (ret--) { // 循環ret次，相當于乘以retstr = addStrings(str, num2);// 累加num2}// 將當前結果加到總和中ans = addStrings(ans, str);// 為下一位做準備：num2后面加0，相當于乘以10（因為下一位是十位，在豎式中要左移一位）num2 += '0';}return ans;
}
int main()
{string num1("123");string num2("456");cout << addStrings(num1,num2) << endl;return 0;
}

字符串加法：

從個位開始逐位相加，處理進位。

結果需要反轉（計算時低位在前）。

乘法實現：

遍歷num1的每一位，將其與num2相乘（通過累加實現）。

每次處理更高位時，在num2末尾補0（等價于左移一位，權重×10）。

方法二：

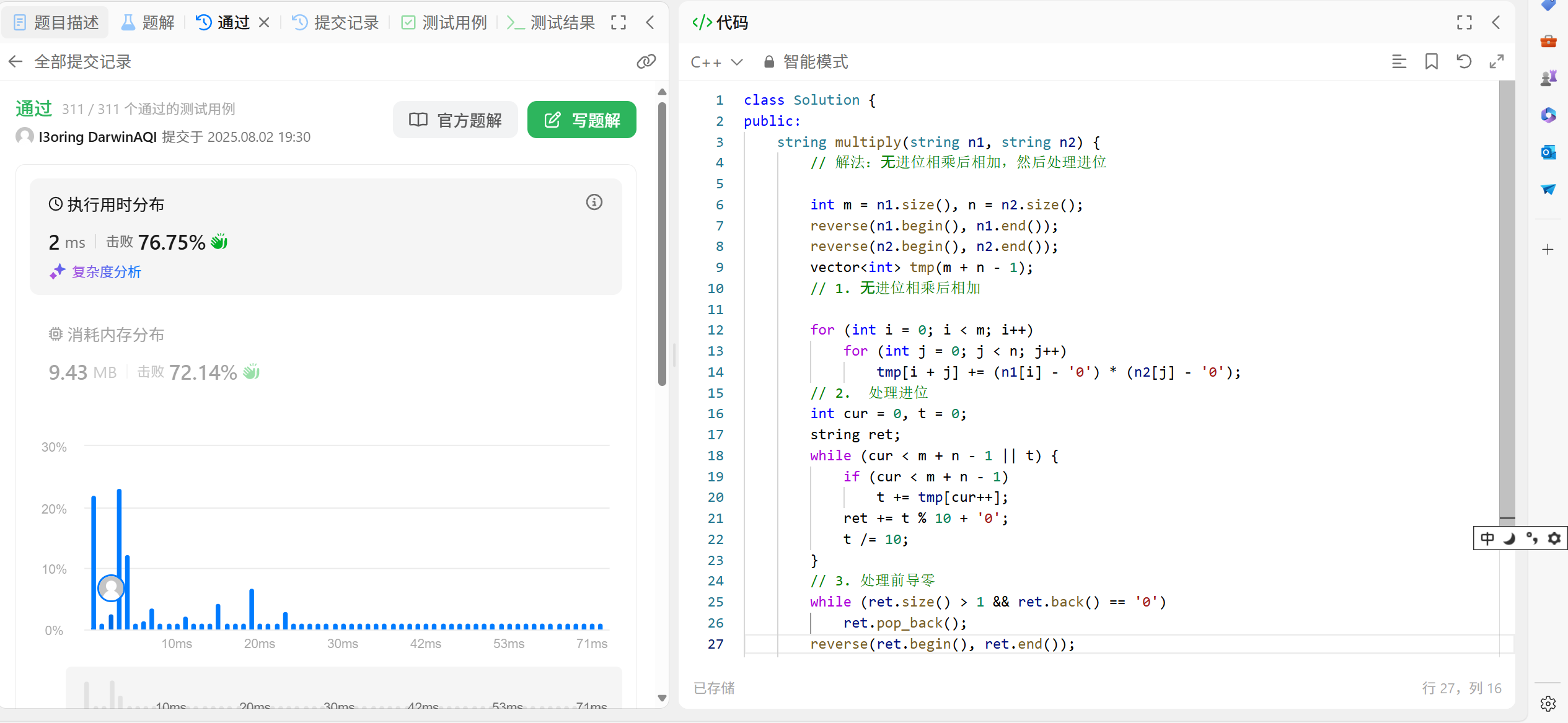
//方法二：在方法一上面進行了改良，優化
string multiply(string n1, string n2)
{// 解法：?進位相乘后相加，然后處理進位int m = n1.size(), n = n2.size();// 反轉字符串，使得低位（個位）在索引0位置reverse(n1.begin(), n1.end());reverse(n2.begin(), n2.end());// 創建臨時數組，大小為m+n-1（因為兩個數相乘，結果位數最小為m+n-1，比如100*100=10000有5位，最大為m+n）// 但這里我們使用m+n-1，后面進位可能會增加位數vector<int> tmp(m + n - 1);// 1. ?進位相乘后相加for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)tmp[i + j] += (n1[i] - '0') * (n2[j] - '0');// 2.  處理進位int cur = 0, t = 0;// cur: 當前處理到tmp的哪個位置，t:進位string ret;// 循環條件：cur還沒到tmp數組末尾，或者還有進位twhile (cur < m + n - 1 || t){if (cur < m + n - 1) t += tmp[cur++]; // 取出當前位的值加入進位t，并移動curret += t % 10 + '0';// 取個位加入結果字符串t /= 10;// 更新進位}// 3. 處理前導零while (ret.size() > 1 && ret.back() == '0') ret.pop_back();reverse(ret.begin(), ret.end());return ret;
}
int main()
{string num1("123");string num2("456");cout << addStrings(num1, num2) << endl;return 0;
}

無進位相乘：

反轉字符串使低位在前（下標0對應個位）。

雙重循環計算n1[i] * n2[j]，結果累加到tmp[i + j]。

統一處理進位：

從低位到高位遍歷tmp，將累加值加上進位后，按位存儲并更新進位。

前導零處理：

刪除結果字符串末尾多余的0（反轉前末尾對應高位）。

反轉字符串使高位在前。

?