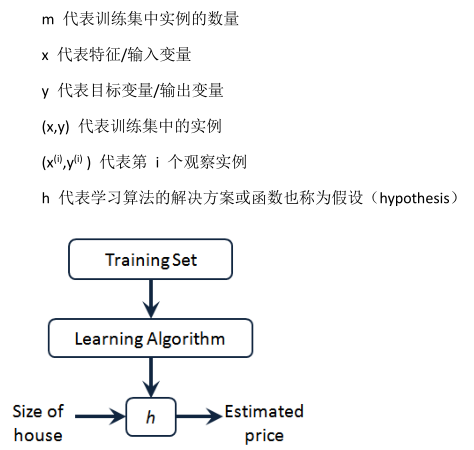
單變量線性回歸(Linear Regression with One Variable)
預測器表達式:
選擇合適的參數(parameters)θ0 和 θ1,其決定了直線相對于訓練集的準確程度。
建模誤差(modeling error):訓練集中,模型預測值與實際值之間的差距。
目標:選出使建模誤差平方和最小的模型參數,即損失函數最小。
損失函數(Cost Function):
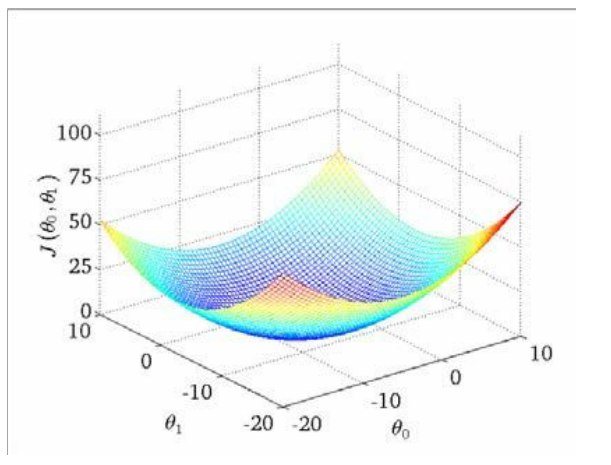
可以看出在三維空間中存在一個使得 J(θ0,θ1)最小的點。
梯度下降算法(Gradient Descent):
批量梯度下降(batch gradient descent)算法的公式為:
總結:
1、先確定預測模型,然后確定損失函數;
2、使用梯度下降算法,讓損失函數最小化,此時的參數可使預測模型的經驗誤差達到最優。
————————————————————————————————————————————————
多變量線性回歸(Linear Regression with Multiple Variables)
為了簡化公式,引入 x0=1。
此時模型中的參數是一個 n+1 維的向量,任何一個訓練實例也都是 n+1 維的向量,特征矩陣 X 的維度是 m*(n+1)。
公式可以簡化為:
多變量線性回歸代價函數,這個代價函數是所有建模誤差的平方和:
多變量線性回歸的批量梯度下降算法為:
即:
開始隨機選擇一系列的參數值, 計算所有的預測結果后, 再給所有的參數一個新的值,如此循環直到收斂。
————————————————————————————————————————————————————————
Feature Scaling
將所有特征的尺度都盡量縮放到-1 到 1 之間。
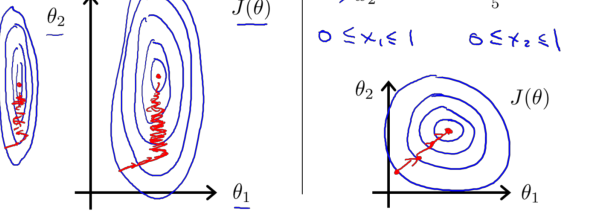
梯度下降算法實踐 2——學習率
梯度下降算法的每次迭代受到學習率的影響:
如果學習率 α 過小, 則達到收斂所需的迭代次數會非常高;
如果學習率 α 過大,每次迭代可能不會減小代價函數,可能會越過局部最小值導致無法收斂。?
通常可以考慮嘗試些學習率:?α=0.01,0.03,0.1,0.3,1,3,10?
————————————————————————————————————————————————————————
多項式回歸(?Polynomial Regression)
線性回歸并不適用于所有數據, 有時需要曲線來適應數據。
比如一個二次方模型:
或者三次方模型:
通常需要先觀察數據然后再決定準備嘗試怎樣的模型。
根據函數圖形特性,還可以使用:
注:如果采用多項式回歸模型,在運行梯度下降算法前,特征縮放非常有必要。
————————————————————————————————————————————————————————
正規方程通過求解下面的方程來找出使得代價函數最小的參數:
假設訓練集特征矩陣為 X(包含了 x0=1),訓練集結果為向量 y
則利用正規方程解出向量:
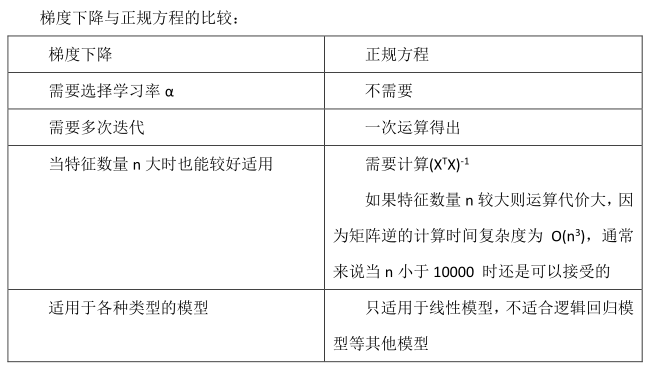
總結:
只要特征變量的數目并不大,標準方程是一個很好的計算參數 θ 的替代方法。?
具體地說, 只要特征變量數量小于一萬, 通常使用標準方程法, 而不使用梯度下降法。
?
隨著學習算法越來越復雜,例如,分類算法,邏輯回歸算法,?并不能使用標準方程法。?
對于那些更復雜的學習算法,將仍然使用梯度下降法。
因此,梯度下降法是一個非常有用的算法,可以用在有大量特征變量的線性回歸問題。
或者在以后課程中,會講到的一些其他的算法,因為標準方程法不適合或者不能用在它們上。?
但對于這個特定的線性回歸模型, 標準方程法是一個比梯度下降法更快的替代算法。
所以,根據具體的問題,以及你的特征變量的數量,這兩種算法都是值得學習的。
不可逆性:
?X'X 的不可逆的問題很少發生
第一個原因:一個線性方程的兩個特征值是線性相關的,矩陣 X'X 不可逆;
第二個原因:用大量的特征值,嘗試實踐學習算法的時候,可能會導致矩陣 X'X 不可逆。
通常,使用一種叫做正則化的線性代數方法,通過刪除某些特征或者是使用某些技術,來解決當 m 比
n 小的時候的問題。即使你有一個相對較小的訓練集,也可使用很多的特征來找到很多合適的參數。?
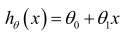
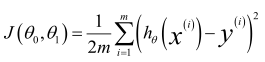
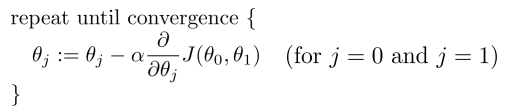
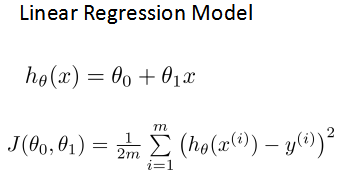


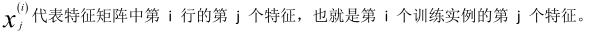
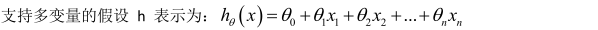
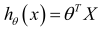
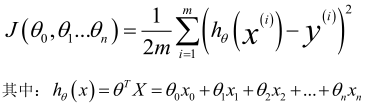

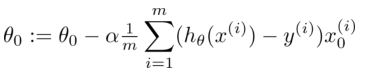
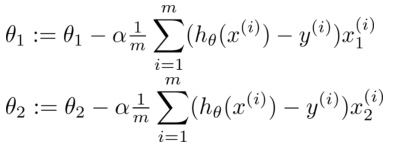
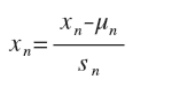

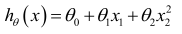
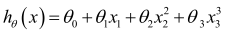
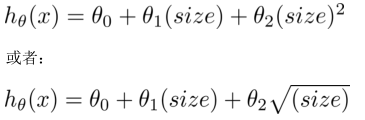
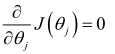
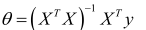







)

又稱為邏輯回歸分析,是分類和預測算法中的一種。通過歷史數據的表現對未來結果發生的概率進行預測。例如,我們可以將購買的概率設置為因變量,將用戶的)







)
--接口測試工具介紹(詳解))
