方格填數
如下的10個格子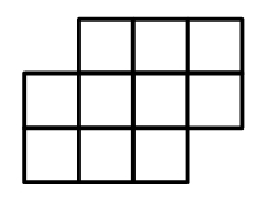
填入0~9的數字,同一數字不能重復填。要求:連續的兩個數字不能相鄰。
(左右、上下、對角都算相鄰)
一共有多少種可能的填數方案?
請填寫表示方案數目的整數。
注意:你提交的應該是一個整數,不要填寫任何多余的內容或說明性文字。
?
解題思路:由題可知,題中的序列是固定的,只有0-9這10個元素,所以可以枚舉其全部全排列,對每個排列根據條件進行篩選。
?
先看一個錯誤答案:520
 (圖一)
(圖一)
一開始想當然的把0-9存入了一維數組中,如圖一,然后發現下標i的上下兩個相鄰位置的坐標為i-4,i+4, 左右為i-1,i+1,
左上右下為i-5,i+5,右上左下為i-3,i+3。于是有了下面的錯誤代碼。
錯誤代碼: ? ? ?(此錯誤代碼運行結果為520)
1 #include <iostream> 2 #include <vector> 3 #include <algorithm> 4 5 using namespace std; 6 7 vector<int>v; 8 int a[8] = { -1,1,-3,3,-4,4,-5,5 }; //一維數組相鄰點的下標 9 10 bool judge() 11 { 12 for (int i = 0; i <= 9; ++i) 13 { 14 for (int j = 0; j < 8; ++j) 15 { 16 int k = i + a[j]; 17 if (k >= 0 && k <= 9) 18 { 19 if (abs(v[k] - v[i]) == 1) //相鄰元素之差的絕對值為1 20 return false; 21 } 22 } 23 } 24 return true; 25 } 26 27 int main() 28 { 29 int cnt = 0; 30 for (int i = 0; i <= 9; ++i) 31 v.push_back(i); 32 33 do 34 { 35 if (judge() == true) 36 cnt++; 37 38 } while (next_permutation(v.begin(), v.end())); 39 40 cout << cnt << endl; 41 42 return 0; 43 }
?
錯因: 忽略了邊界上的坐標,比如7,一直認為左上就是i-5, 但是7-5=2, 但是7并沒有左上方的點。
?
改進: 由于邊界上的坐標比較難處理,所以為了消除邊界的影響,將地圖補全為如下規則圖形,如圖二,這樣就消除了圖二中紅色區域邊界上的影響:
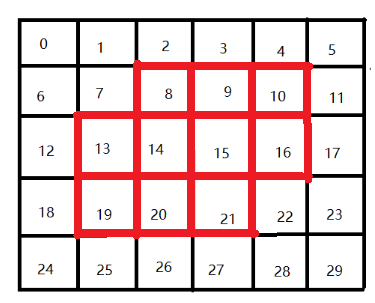 (圖二)
(圖二)
用大小為30的一維數組v保存。?
用一維數組vec保存0-9,對vec進行枚舉全排列,然后將vec[0...9]分別賦值給圖二中的紅色區域,再將非紅色的區域賦值為-10,
對于圖二中的紅色區域,發現下標i的上下兩個相鄰位置的坐標為i-6,i+6, 左右為i-1,i+1,左上右下為i-7,i+7,右上左下為i-5,i+5。
此時再用根據下標獲取其相鄰元素的值,判斷填入的數字是否相鄰即可。
?
改進后的正確代碼:
?
1 #include <iostream> 2 #include <vector> 3 #include <algorithm> 4 5 using namespace std; 6 7 vector<int> v; //補全的圖形 8 vector<int> vec; //未補全的圖形 9 int a[8] = { -1,1,-5,5,-6,6,-7,7 }; //一維數組相鄰點的下標 10 11 bool judge(vector<int> v) 12 { 13 for (int i = 8; i <= 21; ++i) 14 { 15 for (int j = 0; j < 8; ++j) //對其所有相鄰位置進行枚舉 16 { 17 int k = i + a[j]; 18 if (abs(v[k] - v[i]) == 1) //相鄰元素之差的絕對值為1 19 return false; 20 21 } 22 } 23 return true; 24 } 25 26 int main() 27 { 28 int cnt = 0; //方案數 29 for (int i = 0; i <= 9; ++i) 30 vec.push_back(i); //一開始必須升序,是為了保證next_permutation能枚舉所有情況的排列 31 32 for (int i = 0; i <= 29; ++i) 33 v.push_back(-10); 34 35 do 36 { 37 v[8] = vec[0]; v[9] = vec[1]; v[10] = vec[2]; v[13] = vec[3]; v[14] = vec[4]; 38 v[15] = vec[5]; v[16] = vec[6]; v[19] = vec[7]; v[20] = vec[8]; v[21] = vec[9]; 39 40 if (judge(v) == true) 41 cnt++; 42 43 } while (next_permutation(vec.begin(), vec.end())); 44 45 cout << cnt << endl; 46 47 return 0; 48 }
?
正確結果:1580











數組的擴展)







