參數c和gamma的作用

我們通過下圖詳解參數c的作用，首先我們以一個簡單的線性分類器為例，上一個博客中我們知道影響分類器的主要因素是支持向量，即虛線上的樣本，如下圖可知：

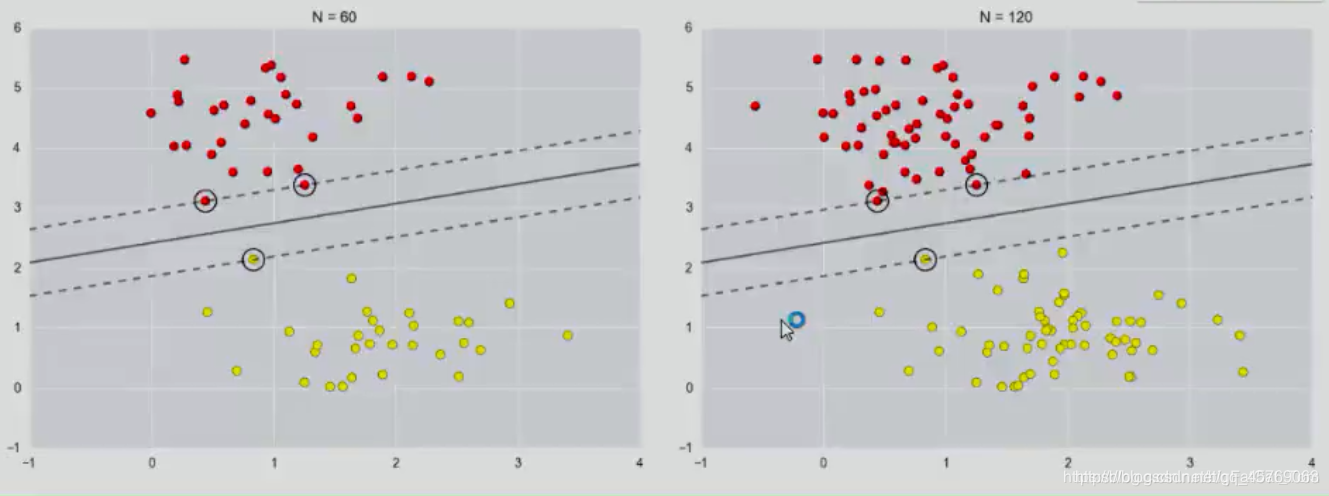
但當正負樣本的分布在如下情況時，需要引入核函數對數據進行高維度的映射，具體如下圖：

?? ?

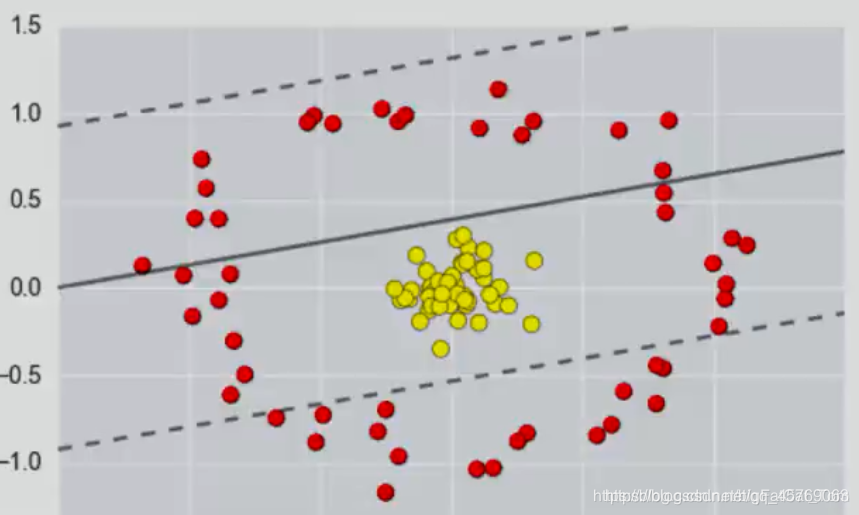
實線為決策平面，虛線上的樣本為支持向量。

參數c

上圖中我們知道決策平面與支持向量之間有一個距離差，而在實際工程中，參數c正是影響了支持向量與決策平面之間的距離，具體效果為：

c越大，分類越嚴格，不能有錯誤

c越小，意味著有更大的錯誤容忍度

具體可以通過下圖展示：

??

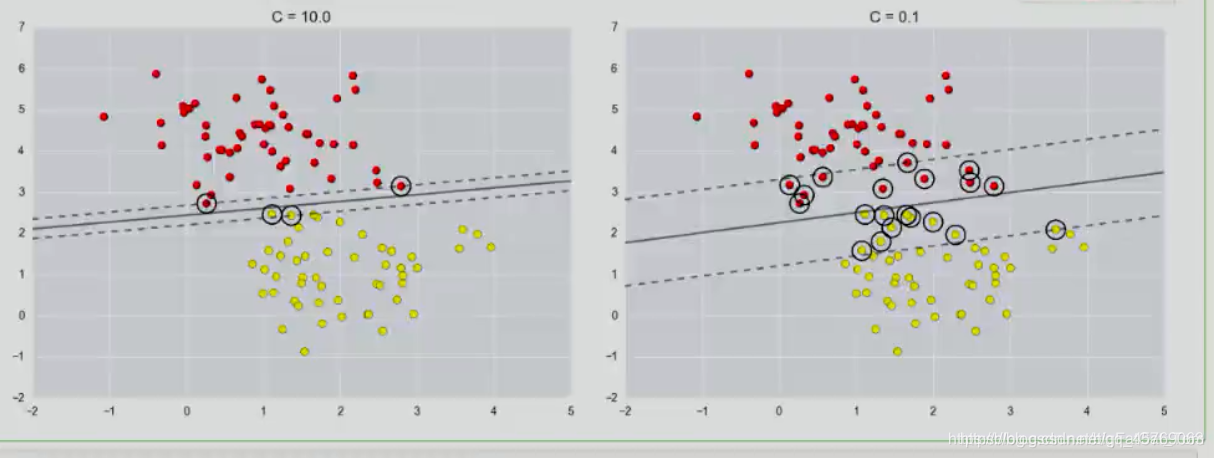
c越大分類結果越好相應的泛化能力降低，c越小，我們的決策邊界更大一些，即在訓練時容忍一些樣本的誤差，拿一些邊界更寬的樣本作為支持向量。

參數gamma

參數gamma主要是對低維的樣本進行高度度映射，gamma值越大映射的維度越高，訓練的結果越好，但是越容易引起過擬合，即泛化能力低。具體效果如下圖表示：

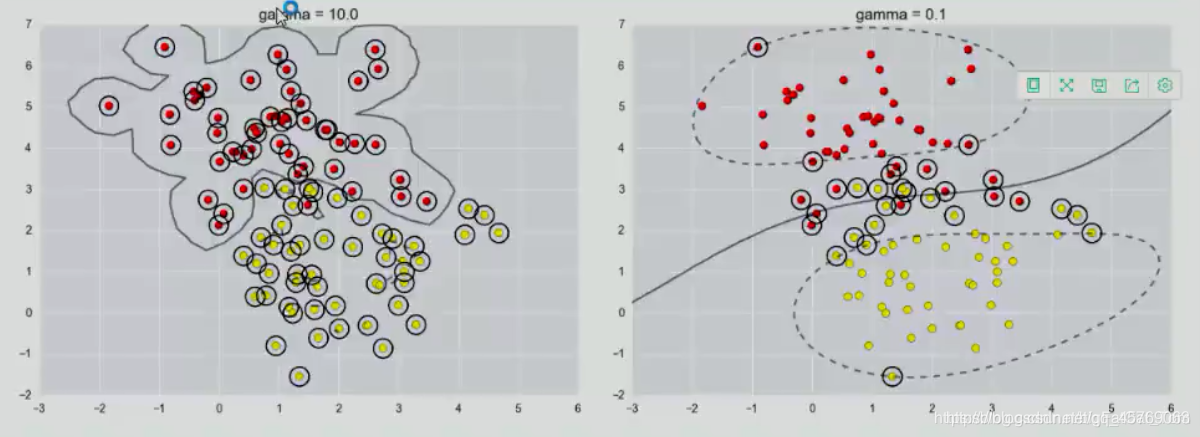
當gamma較大時，決策平面如一個梅花，分類的效果好，但是模型的魯棒性不一定高。

因此我們需要合理的選擇c和gamma的值，使得在訓練結果準確的同時，測試結果同樣相對高，即魯棒性能力強。
總結

在實際工程應用中，我們需要不斷的調整gamma和c的值，并對數據不斷地進行交叉驗證，使得模型的預測結果更高。此時對應的訓練結果w和b作為svm最終的訓練結果。

本文參考：《【機器學習】圖解SVM中gamma和c參數的作用》