目錄
🌼廣度優先遍歷
(1)鄰接矩陣BFS
(2)鄰接表BFS
(3)非連通圖BFS
(4)復雜度分析
🌼深度優先遍歷
(1)鄰接矩陣的DFS
(2)鄰接表的DFS
(3)非連通圖的DFS
(4)復雜度
🌼刷題
📕油田
📕理想路徑
📕騎士的旅程
📕抓住那頭牛
🌼廣度優先遍歷
《啊哈算法第四章之bfs》(17張圖解)-CSDN博客
Breadth First Search,BFS
一層一層地訪問
秘籍:先被訪問的節點,其鄰接點先被訪問
可用隊列實現?
廣度優先遍歷經過的節點和邊,被稱為,廣度優先生成樹
如果遍歷非連通圖,每個連通分量,都會產生一棵廣度優先生成樹
以下代碼結合圖的存儲的結構體進行理解👇
圖的存儲(鄰接矩陣,邊集數組,鄰接表,鏈式前向星)-CSDN博客
(1)鄰接矩陣BFS
void BFS_AM(AMGraph G, int v) // 基于鄰接矩陣的廣度優先遍歷
{int u, w;queue<int>Q; // 創建隊列(先進先出), 存放 intcout << G.Vex[v] << "\t";visited[v] = true;Q.push(v); // 源點 v 入隊while(!Q.empty()) { u = Q.front(); // 取隊頭元素Q.pop(); // 隊頭出隊for (w = 0; w < G.vexnum; w++) { // 遍歷 u 所有鄰接點if (G.Edge[u][w] && !visited[w]) { // u,w 鄰接 且 w 未被訪問cout << G.Vex[w] << "\t";visited[w] = true; // 標記Q.push(w); // 入隊}}}
}(2)鄰接表BFS
void BFS_AL(ALGraph G, int v) // 基于鄰接表的廣度優先遍歷
{int u, w;AdjNode *p; // 鄰接表結構體的指針queue<int>Q; // 創建隊列cout << G.Vex[v].data << "\t";visited[v] = true; // 該鄰接點下標 v 已訪問Q.push(v); // 源點 v 入隊while (!Q.empty()) {u = Q.front(); // 取隊頭元素Q.pop(); // 隊頭出隊p = G.Vex[u].first; // u 的第 1 個鄰接點while (p) { // 依次遍歷 u 所有鄰接點w = p->v; // u 鄰接點下標if (!visited[w]) { // w 未被訪問cout << G.Vex[w].data << "\t";visited[w] = true;Q.push(w); }p = p->next; // u 下一個鄰接點}}
}(3)非連通圖BFS
void BFS_AL(ALGraph G)
{for (int i = 0; i < G.vexnum; i++) { // 檢查未被訪問的點if (!visited[i]) // 以 i 為起點, 再次廣度優先遍歷BFS_AL(G, i); // 基于鄰接表, 也可換鄰接矩陣}
}(4)復雜度分析
基于鄰接矩陣 OR 鄰接表的,空間復雜度,都是 O(n)
都使用一個輔助隊列,每個節點只入隊 1 次,共 n 個節點,所以是 O(n)
時間?
(1)鄰接矩陣
每個節點鄰接表 -> O(n)
共 n 個節點,O(n^2)
(2)鄰接表
d(vi) 為 vi 的出度
每個節點鄰接點 -> O( d(vi) )
有向圖,出度的和 = 邊數 e,所以查找鄰接點為 O(e)
無向圖,所有所有節點的度的和為 2e,即每條邊被記錄 2 次,O(2e),即O(e)
加上初始化的 O(n),總的時間復雜度為 O(n + e)
🌼深度優先遍歷
《啊哈算法》之DFS深度優先搜索-CSDN博客
Depth First Search,DFS
秘籍:后被訪問的節點,其鄰接點先被訪問
通過棧實現,因為遞歸本身就是用棧實現的
當某個節點,沒有未被訪問過的鄰接點時,需要 回退 到上一個節點
(1)鄰接矩陣的DFS
void DFS_AM(AMGraph G, int v) // 節點下標 v
{cout << G.Vex[v] << "\t";visited[v] = true;for (int w = 0; w < G.vexnum; w++) // 依次遍歷 v 所有鄰接點if (G.Edge[v][w] && !visited[w]) // v, w鄰接, 且 w 未被訪問DFS_AM(G, w); // w 節點出發, 遞歸深度優先遍歷
}(2)鄰接表的DFS
void DFS_AL(ALGraph G, int v)
{AdjNode *p; // AdjNode 鄰接點結構體cout << G.Vex[v].data << "\t";visited[v] = true;p = G.Vex[v].first; // v 的第 1 個鄰接點while(p) { // 依次遍歷 v 所有鄰接點int w = p->v; // w 為 v 鄰接點下標if (!visited[w]) // w 未被訪問DFS_AL(G, w); // w出發, 遞歸深度優先遍歷// 由上面DFS, 先被訪問節點, 鄰接點后被訪問p = p->next; // v 下一鄰接點}
}(3)非連通圖的DFS
void DFS_AL(ALGraph G)
{for (int i = 0; i < G.vexnum; i++) {if (!visited[i])DFS_AL(G, i); // i 出發, 繼續DFS}
}(4)復雜度
鄰接矩陣,時間 O(n^2),空間 O(n)
鄰接表,時間 O(n + e),空間 O(n)?
圖和鄰接矩陣是唯一對應的,那么,基于鄰接矩陣的BFS和DFS,也唯一對應
但是鄰接表,會因為? 邊的輸入順序 OR 正序逆序建表,的不同,影響鄰接表中鄰接點的順序,所以,基于鄰接表的BFS,DFS,的序列不唯一
🌼刷題
📕油田
Oil Deposits - UVA 572 - Virtual Judge (vjudge.net)
思路?
(1)兩層 for 遍歷所有位置,如果該位置,未標記連通分量 且 是油田 '@',從這個位置開始DFS
(2)每次DFS開始前,需要判斷是否出界
(3)水平 / 垂直 / 對角線,算作相鄰,那么從一個位置出發,有?8 個方向需要 DFS
解釋
(1)連通分量
比如 setid[x][y] = 1,(x, y) 表示一個點,如果這一堆點 setid[][] 都是 1,那么它們屬于同一個連通分量,利用 cnt++,cnt 從0開始,最后輸出 cnt 即可,表示有 cnt 個油藏
(2)坑
a. 每次 dfs 都要給該點的?setid 標記非 0 值,所以,每個 dfs 開頭,要對?
“已有連通分量 || 不是油田” 的情況,進行 return
b. 每次 cin >> m >> n 后,記得 memset setid 數組(多組輸入常犯錯誤)
AC? 代碼?
#define REP(i,b,e) for(int i=(b); i<=(e); i++)
#include<iostream>
#include<cstring>
using namespace std;const int N = 110;
string str[N]; // 字符矩陣
int m, n, setid[N][N]; // 行, 列, 連通分量void dfs(int x, int y, int cnt)
{// 出界if (x < 0 || y < 0 || x >= m || y >= n) return; // 已有連通分量 OR 不是油田if (setid[x][y] || str[x][y] != '@') return;// 標記setid[x][y] = cnt;// 遞歸遍歷 8 個方向REP(i,-1,1)REP(j,-1,1) {if (!i && !j) continue; // 同時為0, 原來的點dfs(x+i, y+j, cnt);}
}int main()
{while(cin >> m >> n) {if (!m && !n) break;// 初始化memset(setid, 0, sizeof(setid));int cnt = 0; // 油藏數量// 讀入字符矩陣REP(i,0,m-1) // m 行cin >> str[i];// 對每個點 dfsREP(i,0,m-1)REP(j,0,n-1) // n 列if (!setid[i][j] && str[i][j] == '@') // 未標記且油田dfs(i, j, ++cnt);cout << cnt << endl;} return 0;
}📕理想路徑
理想路徑 Ideal Path - 洛谷 | 計算機科學教育新生態 (luogu.com.cn)
Ideal Path - UVA 1599 - Virtual Judge (vjudge.net)
基于BFS的最短路徑算法。它首先進行逆向標高求最短距離,然后求解經過邊的顏色序列最小,即字典序最小
具體意思是:比如 3 5 1 9 9? < 3 5 2 1 1
求的是,最小字典序的序列,而不是最小權值和
結合題目就是👇
采取 BFS,因為 邊權為 1
本題采用 鏈式前向星 存儲
? bfs1() + bfs2()
隊列 q1:鄰接邊終點
隊列 q2:鄰接邊邊權(顏色的值)
隊列 q3:最小邊權終點
總體脈絡
看著很復雜,其實很多重復的代碼?
(1)你需要知道 鏈式前向星 的存圖方式
(2)訪問鄰接點的代碼(板子)
(3)BFS 的代碼(板子)
(4)bfs1() 和 bfs2(),都需要 vis[] 防止重復訪問已訪問過的點
(5)bfs1() 從終點出發,找到每個點到終點的最小距離
(6)add() 加邊(板子)
bfs2() 從起點出發,按照 距離-1 的方向,找到邊的最小權值的點,再從這些點,再次擴展
關于為什么,不能從起點找最短距離( bfs1() ),我還不是很理解,因為沒有現成的例子
先記板子吧
想要非常流暢地敲出來,一遍AC,你需要熟記
1,鏈式前向星的板子(add() 加邊,struct結構體,訪問鄰接點)
2,BFS 遍歷圖的板子
AC? 代碼
評測系統有點問題,《算法訓練營》源碼 OR 洛谷題解代碼,都是 Unknown Error 或者 Runtime Error,所以,過了樣例就當 AC 了吧?
#include<iostream>
#include<cstring> // memset()
#include<queue>
using namespace std;const int N = 1e5 + 10, M = 2e5 + 10, inf = 0x7fffffff;int n, m, cnt; // 節點數, 邊數, 邊的計數
int head[N], dis[N]; // 鄰接表頭節點, 節點到終點最短距離
bool vis[N];
queue<int> q1, q2, q3; // q1鄰接邊終點, q2邊權, q3最小邊權終點struct Edge
{int to, c, next; // 邊的終點, 邊權, 下一條邊索引
}e[M]; // 邊數組void add(int u, int v, int c) // 起點u, 終點v, 邊權c
{// 邊的下標 1 開始e[++cnt].to = v; // 終點e[cnt].c = c; // 權值// 頭插法(倒序插入)e[cnt].next = head[u]; // 下一條邊索引head[u] = cnt; // 更新頭節點的第 1 條邊
}void bfs1() // 逆向求最短距離
{int u, v; // 邊的起點, 終點memset(vis, 0, sizeof(vis)); // 初始化標記數組dis[n] = 0;q1.push(n); // 終點加入隊列vis[n] = 1; while (!q1.empty()) {u = q1.front(); // 取隊首q1.pop();vis[u] = 1;// 從節點第 1 條邊開始, 依次遍歷鄰接點for (int i = head[u]; i; i = e[i].next) {v = e[i].to; // 邊終點編號, 即鄰接點編號if (vis[v]) continue; // 防止重復訪問dis[v] = dis[u] + 1; // 更新鄰接點到終點最短距離q1.push(v);vis[v] = 1;}}
}void bfs2() // 正向求最小字典序
{int u, v, minc, c; // 邊的起點, 終點, 最小邊權, 邊權bool first = 1; // 第 1 個邊權前不要空格memset(vis, 0, sizeof(vis));vis[1] = 1;// 遍歷 起點 鄰接點 -- 類似初始化, 為后續循環提供條件for (int i = head[1]; i; i = e[i].next) if (dis[e[i].to] == dis[1] - 1) { // 往終點方向距離 -1 的點q1.push(e[i].to); // 加入鄰接點q2.push(e[i].c); // 加入邊權}while (!q1.empty()) { // 隊列不為空, 未擴展完minc = inf; // 最小初始化為無窮大// 尋找當前隊列最小邊權while (!q1.empty()) {v = q1.front(); // 取鄰接點下標q1.pop(); c = q2.front(); // 取邊權q2.pop();if (c < minc) {// 先清空 q3while (!q3.empty()) q3.pop();minc = c; // 更新最小邊權}if (c == minc) q3.push(v); // 所有邊權是最小值的鄰接點, 都加入 q3}// 輸出路徑邊權if (first) first = 0; // 第 1 個邊權前, 不輸出 空格else cout << " ";cout << minc; // 對,最小邊權的鄰接點, 進行擴展while (!q3.empty()) {u = q3.front(); q3.pop(); // 取隊首if (vis[u]) continue;vis[u] = 1;// 遍歷最小邊權鄰接點的, 每一個鄰接點for (int i = head[u]; i; i = e[i].next) {v = e[i].to;if (dis[v] == dis[u] - 1) { // 往終點距離 -1 的點q1.push(v); // 鄰接點入隊列q2.push(e[i].c); // 邊權入隊}}}}
}int main()
{int u, v, c;while (cin >> n >> m) { // 多組輸入// dis[] 在 bfs1() 被更新, vis[] 在1, 2都有被更新memset(head, 0, sizeof(head)); // 更新 頭節點數組cnt = 0; // 更新邊的計數// 添加邊for (int i = 1; i <= m; ++i) {cin >> u >> v >> c; // 起點, 終點, 邊權add(u, v, c), add(v, u, c); // 無向}bfs1(); // 反向求最短距離cout << dis[1] << endl; // 起點到終點最短距離bfs2(); // 根據最短距離, 求最小字典序cout << endl; // 多組輸入}return 0;
}
📕騎士的旅程
鏈接?
2488 -- A Knight's Journey (poj.org)
A Knight's Journey - POJ 2488 - Virtual Judge (vjudge.net)
題解?
馬走日,可以在棋盤,任一地方開始和結束
為了字典序最小,只需要從 A1 開始DFS
貼幾個題解博客👇
POJ 2488 - A Knight's Journey | 眈眈探求 (exp-blog.com)
POJ2488-A Knight's Journey(DFS+回溯)-騰訊云開發者社區-騰訊云 (tencent.com)
解釋1
解釋下代碼中的 return flag = 1;
等價于? ? flag = 1; return flag;?
還有就是 dfs() 中, if() 的判斷條件 !flag,因為 if() 里面還有 dfs() 遞歸,如果不加上 !flag 的判斷,會得到所有路徑,而不只是按字典序排序的第 1 條路徑
2?
題目分析(騰訊云):?
1. 應該看到這個題就可以想到用DFS,當首先要明白這個題的意思是能否只走一遍(不回頭不重復)將整個地圖走完,而普通的深度優先搜索是一直走,走不通之后沿路返回到某處繼續深搜。所以這個題要用到的回溯思想,如果不重復走一遍就走完了,做一個標記,算法停止;否則在某種DFS下走到某一步時按馬跳的規則無路可走而棋盤還有為走到的點,這樣我們就需要撤消這一步,進而嘗試其他的路線(當然其他的路線也可能導致撤銷),而所謂撤銷這一步就是在遞歸深搜返回時重置該點,以便在當前路線走一遍行不通換另一種路線時,該點的狀態是未訪問過的,而不是像普通的DFS當作已經訪問了
2.?如果有多種方式可以不重復走一遍的走完,需要輸出按字典序最小的路徑,而注意到國際象棋的棋盤是列為字母,行為數字,如果能夠不回頭走一遍的走完,一定會經過A1點,所以我們應該從A1開始搜索,以確保之后得到的路徑字典序是最小的(也就是說如果路徑不以A1開始,該路徑一定不是字典序最小路徑),而且我們應該確保優先選擇的方向是字典序最小的方向,這樣我們最先得到的路徑就是字典序最小的。
3?
本題 dfs() 中,最后只需要 vis[][] = 0;?
用來取消標記,便于回溯
那么為什么不需要對 path[step][0] 和 path[step][1] 歸0呢
因為每次新的 dfs( , , step) 遞歸時,會對上一步的 path 進行覆蓋
4
if (!flag) { // 關鍵一步, 否則輸出的不是第 1 條路徑代碼第 23 行,dfs() 中,每一步遞歸前,都需要判斷,是否已經滿足字典序順序的第 1 條路徑?
5
// int dir[8][2] = {1,2,1,-2,-1,2,-1,-2,2,1,2,-1,-2,1,-2,-1};
int dir[8][2]={-2,-1,-2,1,-1,-2,-1,2,1,-2,1,2,2,-1,2,1}; // 方向數組也要按字典序注釋掉的方向數組,沒按字典序,因為字典序的第 1 條路徑,必須保證,行 / 列 盡可能的小
所以行從 -2 到 -1 到 1 到 2,列也是依次小到大
AC? 代碼
#include<iostream>
#include<cstring>
using namespace std;// 列 行 標記數組 滿足條件 輸出路徑
int m, n, vis[30][30], flag, path[30][2];
// int dir[8][2] = {1,2,1,-2,-1,2,-1,-2,2,1,2,-1,-2,1,-2,-1};
int dir[8][2]={-2,-1,-2,1,-1,-2,-1,2,1,-2,1,2,2,-1,2,1}; // 方向數組也要按字典序int dfs(int x, int y, int step) // (x, y), 第 step 步
{if (step == n*m) { // 步數 = 格子總數// return flag = 1;flag = 1;return flag;}// 遍歷 8 個方向for (int i = 0; i < 8; ++i) {int tx = x + dir[i][0];int ty = y + dir[i][1];if (tx < 1 || tx > n || ty < 1 || ty > m || vis[tx][ty]) // 注意行列反轉continue; // 越界 或 已訪問if (!flag) { // 關鍵一步, 否則輸出的不是第 1 條路徑// 標記vis[tx][ty] = 1;path[step][0] = tx;path[step][1] = ty;// 遞歸dfs(tx, ty, step + 1);// 取消標記(回溯)vis[tx][ty] = 0;}}return flag;
}int main()
{int t, cnt = 1;cin >> t;while (t--) {cin >> m >> n;// 初始化memset(vis, 0, sizeof(vis)); flag = 0;// 起點 (1 ,1) 加入 pathpath[0][0] = 1; path[0][1] = 1; vis[1][1] = 1; // 起點已走過cout << "Scenario #" << cnt++ << ":" << endl;if (dfs(1, 1, 1)) // 1,1 是起點, 第 3 個參數, 起點算 1 步for (int i = 0; i < n*m; ++i)cout << char(path[i][0] + 'A' - 1) << path[i][1]; // 記得 -1else cout << "impossible";cout << endl << endl; // 兩次換行, 才有間隔一行的效果}return 0;
}📕抓住那頭牛
3278 -- Catch That Cow (poj.org)
Catch That Cow - POJ 3278 - Virtual Judge (vjudge.net)
一道很好的,加深對 DFS 和 BFS 理解的,簡單題(當然,首先要找規律)?
(1)n 為 0,只能先往前走 1 步,此時 n = 1,ans++
(2)分類討論
dfs(t) 表示人位置 n,到位置 t 的最小步數
1)?t <= n,只能一步一步后退,需要 n - t 步
2)t 為偶數,取 min( dfs(t/2) + 1, t - n?)
3)t 為奇數,取 min( dfs(t - 1) + 1, dfs(t + 1) + 1?)
int dfs() 中 return 即可
AC? DFS
#include<iostream>
#include<cmath>
using namespace std;int n, k, ans; // n 人位置, k 牛位置int dfs(int t) // t 牛位置
{if (t <= n) return n - t;if (t % 2) {// cout << t << endl;return min(dfs(t-1) + 1, dfs(t+1) + 1);}else if (t % 2 == 0) {// cout << t << endl;return min(dfs(t/2) + 1, t - n);}return -1; // 非法返回
}int main()
{cin >> n >> k;if (n == 0) n = 1, ans++; ans += dfs(k);cout << ans;return 0;
}
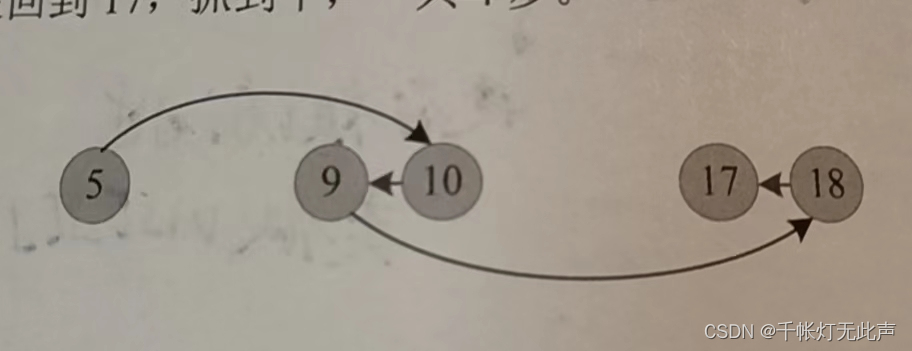
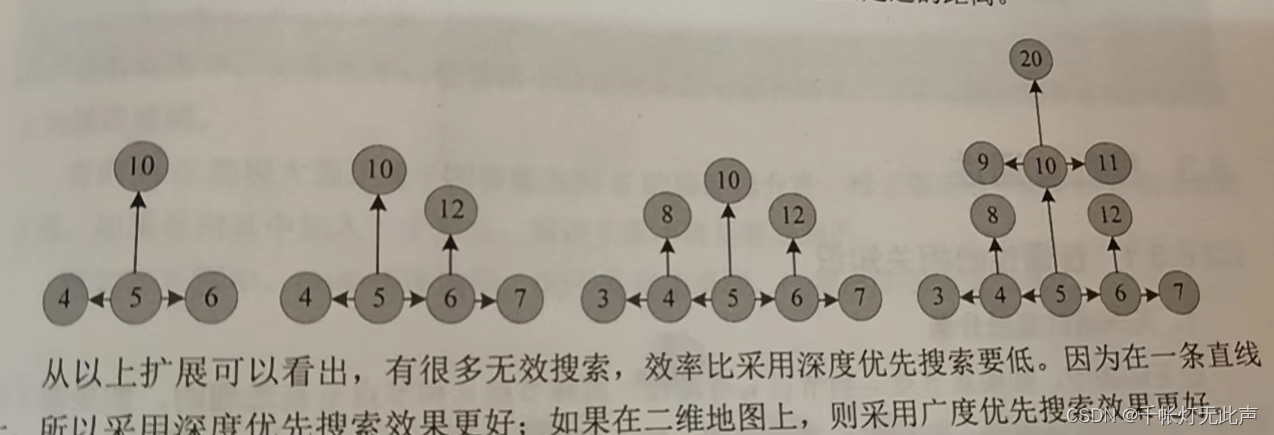
(1) k <= n,只能一步一步后退,輸出 n - k
(2)從 人的位置 n 開始 BFS,每個節點可以擴展 3 個位置
👆上圖,從 人的位置 5 開始,第一次擴展得到 4, 6, 10,第二次擴展,再分別從4,6,10開始
AC? BFS
#include<iostream>
#include<queue>
using namespace std;const int N = 1e5 + 10;
int n, k, d[N], vis[N]; // d[] 答案數組, vis[] 標記數組void bfs()
{queue<int> q;// 當前位置加入隊列d[n] = 0; // 距離(時間)為 0vis[n] = 1; // 已訪問q.push(n); // 起點入隊while (!q.empty()) { // 直到擴展到目標點, 或者訪問完所有點int u = q.front(); q.pop(); // 取隊頭if (u == k) { // 到達目標點cout << d[u]; return;}// 每個節點可以擴展 3 個位置int x;// 左一步x = u - 1;if (x >= 0 && x <= 1e5 && !vis[x]) { // 不超限 且 未訪問// 加入隊列d[x] = d[u] + 1; // 時間 + 1vis[x] = 1; // 標記q.push(x);}// 右一步x = u + 1;if (x >= 0 && x <= 1e5 && !vis[x]) {d[x] = d[u] + 1;vis[x] = 1;q.push(x);}// 坐車 * 2x = u * 2;if (x >= 0 && x <= 1e5 && !vis[x]) {d[x] = d[u] + 1;vis[x] = 1;q.push(x);}}
}int main()
{cin >> n >> k; // n 人位置, k 牛位置if (k <= n) cout << n - k;else {bfs();}
}







)



)


:Tair安裝部署)


X的區別是?)

)

