目錄
1.快速了解的例子：?
（1）假設所有節點的初始特征都是[1, 0, 0]? ，那么AX的結果是：
（2）?的結果是：
(3)? 總結：
2.計算結構系數的例子
（1）源代碼的計算形式是：
? (2) 正常的AX是:
（3）? ?A轉置以后發現和上面的源代碼的 X 是一致的；僅僅展示轉換后的結果；
3.總結：
1.快速了解的例子：?
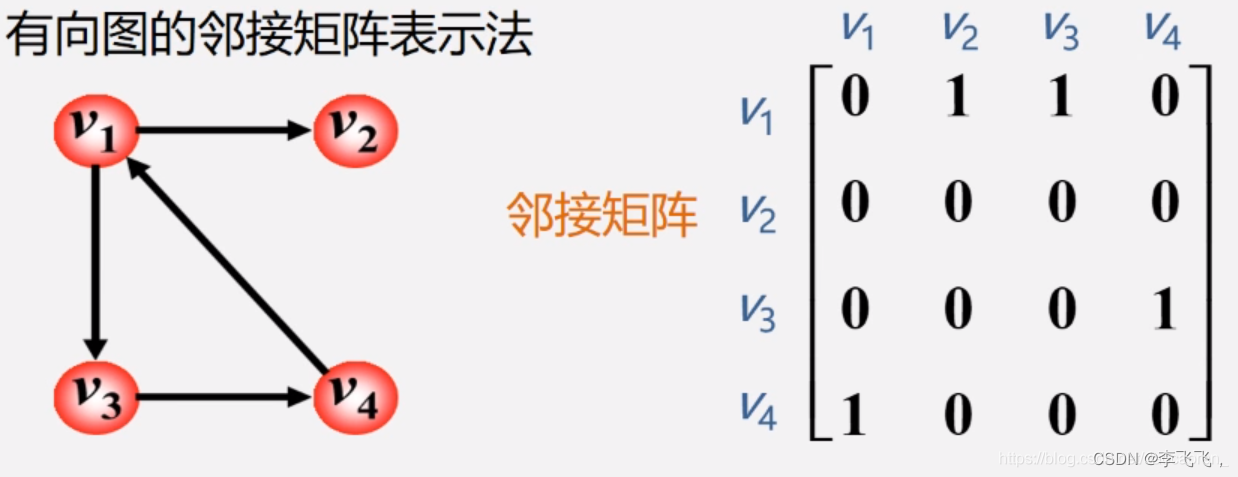
來看這個例子：
目標節點是有向邊箭頭指向的點。在有向圖中，每條有向邊都有一個起點和一個終點，起點被稱為源節點，終點被稱為目標節點。箭頭從源節點指向目標節點，表示數據或信息從源節點流向目標節點。
（1）假設所有節點的初始特征都是[1, 0, 0]? ，那么AX的結果是：
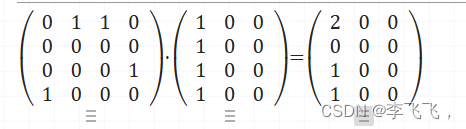
可以看到每一行的結果表示的是從目標節點傳出的信息的和
（2）
?的結果是：
這里每一行的結果才是從源節點（鄰居節點）傳入目標節點的信息。
(3)? 總結：
pytorch geometric中為何要將稀疏鄰接矩陣寫成轉置的形式adj_t？
原因就是：
- 首先?
pytorch geometric?的邊信息可以有兩種存儲模式，第一種是edge_index，它的shape是[2, N]，其中?N?是邊的數目。第一個N維的元素存儲邊的原點的信息，稱為source，第二個N維的元素存儲邊的目標點的信息，稱為target。?舉個例子，如果我們有以下這樣一張有向圖，那么edge_index是這樣的:?tensor([[1, 2, 3, 4], [0, 0, 0, 0]])，邊是(1,0), (2,0), (3,0), (3,0)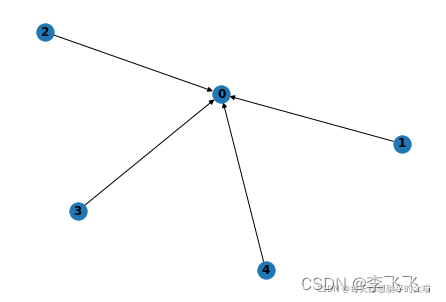 
- 如果以上的圖是無向圖的話，那么0這個節點也指向1,2,3,4這幾個節點，edge_index則應該是這樣的: tensor([[1, 2, 3, 4,0, 0, 0, 0], [0, 0, 0, 0, 1, 2, 3, 4]])，邊是(1,0), (2,0), (3,0), (3,0), (0,1), (0,2), (0,3), (0,4)。edge_index這么寫的原因是，在pytorch geometric中，用scatter一類的方式可以很方便地實現，從source到target，這種默認的邊傳遞方式。（當然傳遞方式你也可以改成從target傳遞到source。）
pytorch geometric的邊信息的第二種存儲模式是adj_t，它是一個sparse tensor。這里我們看到作者在adj后面加上了t，說明它是鄰接矩陣的轉置。為什么要寫成轉置呢，我們接著上面edge_index講- edge_index中信息傳遞是source to target，也就是edge_index[0] to edge_index[1]，而adj計算的是將原圖的有向邊的方向調轉以后的新圖：然后得到新圖上從鄰居節點到目標節點聚合的消息。所以在做矩陣計算傳遞信息的時候，作者將 adj 轉換成adj_t ，并且將它作為默認形式，這樣計算的也就是從源節點到目標節點的信息和，這樣就保持了一致。
2.計算結構系數的例子
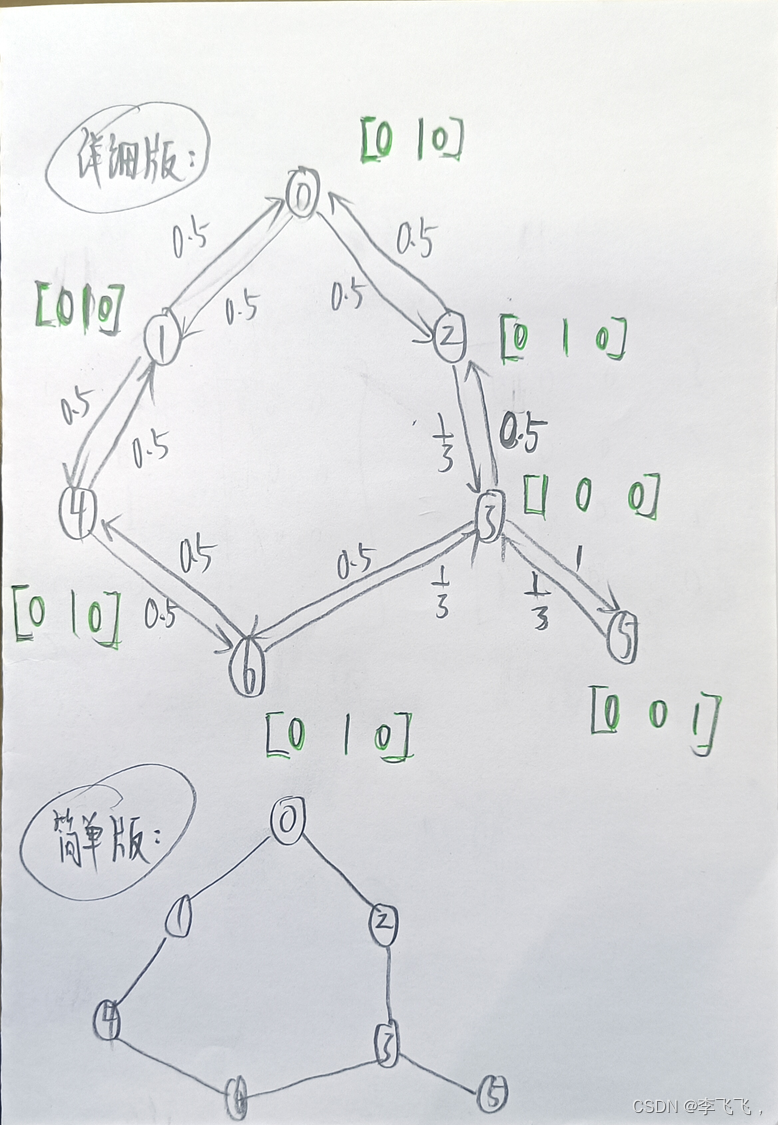
節點的度數作為節點的初始特征
傳入各節點的消息（不算自己）：
- 0：[0,1,0]*0.5+[0,1,0]*0.5 = [0, 1, 0]
- 1:? ?[0,1,0]*0.5+[0,1,0]*0.5 =?[0, 1, 0]
- 2:? [0,1,0]*0.5+[1,0,0]*0,5 =[1/2, 1/2, 0]
- 3:? [0,1,0]*1/3+[0,1,0]U*1/3+[0,0,1]*1/3=[0, 2/3, 1/3]
- 4:? [0,1,0]*0.5+[0,1,0]*0.5 =?[0, 1, 0]
- 5:? [1,0,0]*1= [1,0,0]
- 6:?[0,1,0]*0.5+[1,0,0]*0,5 =[1/2, 1/2, 0]
（1）源代碼的計算形式是：
這里的A不是標準的A，是weight,在計算的結構系數時候，weight[node][index]表示的是鄰居 index 對與目標節點 node的重要程度。結果是：
? (2) 正常的AX是:
計算的將原圖的有向邊的方向調轉以后的新圖：然后得到新圖上從鄰居節點到目標節點聚合的消息。
（3）? ?A轉置以后發現和上面的源代碼的 X 是一致的；僅僅展示轉換后的結果；
所以源代碼的計算結果沒錯的。我的思路也是對的。
??算的是正兒八經的原圖的從源節點（鄰居節點）到目標節點的信息。
3.總結：
- 對于無向圖來說，A默認邊上的權重都為1，所以A和A的轉置結果一致，其中在PYG中，有向圖還是作為有向圖去處理了，上邊edge_index的例子就是最好的說明。
- 當遇到有向圖，尤其是節點之間互相有邊，邊上的權重還不一樣，那么就要注意將A轉換為A的轉置進行矩陣乘法。
參考的文章有：
pytorch geometric中為何要將稀疏鄰接矩陣寫成轉置的形式adj_t_pytorch中的稀疏矩陣為什么要轉置-CSDN博客
)
