賽前需要對所有經典模型有基本了解，如適用范圍、基本原理和實現步驟，做到比賽時能夠根據問題確定何種模型進行研究。

(1)層次分析法 (AHP)——? 評價/決策問題

層次分析法是將定性問題定量化處理的一種有效手段，因此它可以廣泛用于 評價問題和決策問題。面臨各種各樣的方案，要進行比較、判斷、評價、最后作 出決策，例如去某地旅游要考慮景色、費用、居住、飲食和旅途等費用，不同地 區在這些方面各有特點，如果只是憑借經驗處理這些問題，主觀性較強，不能使

人信服。

第一步：建立層次結構模型

一般分為三層，最上面為目標層，最下面為方案層，中間是準則層或指標層。

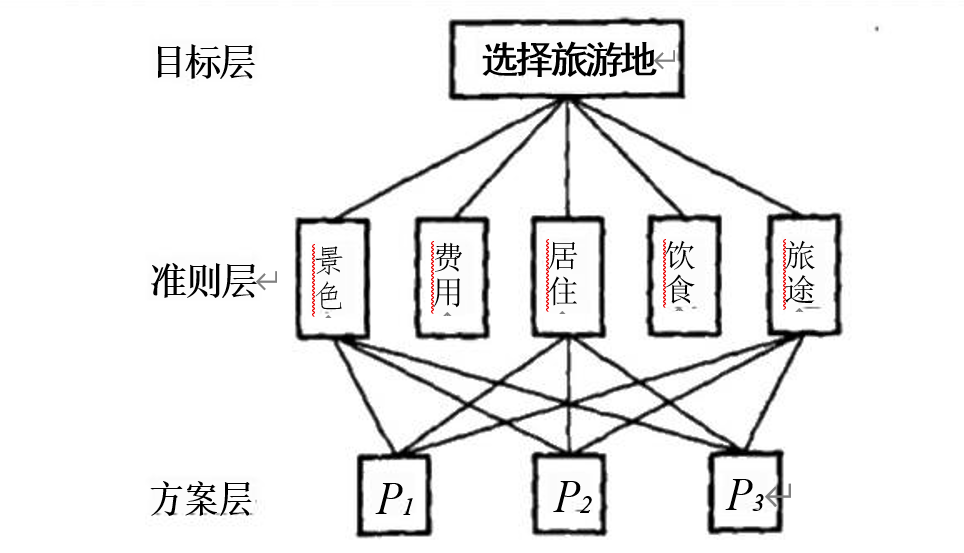
注意：在層次劃分及因素選取時，上層對下層有支配作用；同一層因素不存

在支配關系(相互獨立);每層因素一般不要超過9個。

第二步：構造成對比較陣

要比較n 個因素對目標的影響，我們要確定它們在目標層中所占的比重(權 重)圖片，可以用兩兩比較的方法將各因素的重要性量化(兩個東西進行比較，

最能比較出它們的優劣及優劣程度)。如何確定?

	重要性相同	稍微重要	重要	非常重要	絕對重要
aij	1	3	5	7	9

最終形成比較矩陣：

第三步： 一致性檢驗

在給出成對比較矩陣的時候存在一定主觀性，因此需要通過一致性檢驗判斷

成對比較矩陣的合理性。

1、計算一致性指標 CI

用來衡量成對比較矩陣的不一致程度。

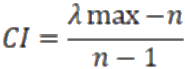
2、 查找相應的平均隨機一致性指標RI。

n	1	2	3	4	5	6	7	8	9
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45

3、計算一致性比例CR。

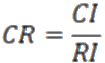
CR<0.1時，認為矩陣?A 的不一致性是可以接受的，反之，應該修改成對比

較矩陣。

第四步：計算權重向量

求矩陣A 的最大特征值所對應的向量，并歸一化，即可作為權向量。權向量 的各個權重就是決策層對目標層的影響大小。把每一層對上一層的權重依次乘起來，即可得到最終的權向量，有大到小排列即可得到評價標準或者決策方案。

注意：

1、層次分析法只能從現有的方案中選擇出較優的一個，并不能提供出一個新的或是更好的方案來；

2、 建立層次結構及成對比較矩陣，主觀因素起很大作用，這是一個無法克 服的缺點，因此建議比賽時如果要用這種方法，可以在網上查找充足的資料，再 由小組共同打分或者單獨打分取平均值，以此規避主觀性，此外， 一致性檢驗必不可少。

(2)狄克斯特拉 (Dijkstra)??????

算法- — 最短路問題

最短路問題是圖論應用的基本問題，很多實際問題，如線路的布設、運輸安 排、運輸網絡最小費用流等問題，都可通過建立最短路問題模型來求解。Dijkstra 算法采用的是一種貪心的策略，為了在計算機上描述圖與網絡，我們采用鄰接矩陣表示法，其中鄰接矩陣是表示頂點之間相鄰關系的矩陣，記為

W=(W?),n

聲明一個數組dis 來保存源點到各個頂點的最短距離和一個保存已經找到了最短路徑的頂點的集合： T。初始時，原點 s?? 的路徑權重被賦為0 (dis[s]=0)。若對于頂點 s 存在能直接到達的邊(s,m),? 則把dis[m]設 為w(s,m)同時把所有其他 (s 不能直接到達的)頂點的路徑長度設為無窮大。即根據距離給W 賦權：

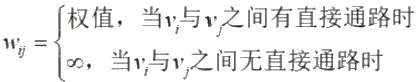
初始時，集合T 只有頂點s 。然后從dis? 數組選擇最小值，則該值就是源點 s 到該值對應的頂點的最短路徑，并且把該點加入到T 中，此時完成一個頂點。 然后我們需要查看新加入的頂點是否可以到達其他頂點，并且查看通過該頂點到 達其他點的路徑長度是否比原點直接到達短?如果是，那么就替換這些頂點在 dis? 中的值，然后又從dis? 中找出最小值，重復上述動作，直到T中包含了圖的所有頂點。

(3)k-??? 近鄰算法 (KNN)——? 聚類問題

聚類問題常見于數據處理，聚類算法通過感知樣本間的相似度，進行歸類歸 納，對新的輸入進行輸出預測，輸出變量取有限個離散值。KNN 是一種基于實例 的監督學習算法，選擇合適的參數 k 就可以進行應用。k 近鄰法的特殊情況是 k=1的情形，稱為最近鄰算法。

優點：?精度高、對異常值不敏感、無數據輸入假定；?缺?點?：計算復雜度高、空間復雜高。

算法三要素： k 值的選擇、距離度量、分類決策規則。如果選擇較小的值，? 分類結果會對近鄰的實例點非常敏感，如果鄰近的實例點恰巧是噪聲，分類就會 出錯；如果選擇較大的值，與輸入實例較遠的(不相似的點)也會對分類產生影響，使分類發生錯誤。關于如何選擇合適的k,? 沒有固定的計算方法，而是依賴經驗。

距離的度量一般采用歐氏距離，優點在于計算量小，容易解釋且足夠準確。 分類決策規則采用“投票法”,即選擇這k 個樣本中出現最多的類別標記作為預 測結果或者采用”平均法”,即將k 個樣本的實值輸出標記平均值作為預測結果；還可基于距離遠近進行加權平均或加權投票，距離越近的樣本權重越大

(4)灰色預測—— 預測模型

對于一些預測問題，如氣象預報、地震預報、病蟲害預報等可以用灰色預測模型解決。

灰色預測是一種對含有不確定因素的系統進行預測的方法。灰色預測通過鑒 別系統因素之間發展趨勢的相異程度，即進行關聯分析，并對原始數據進行生成 處理來尋找系統變動的規律，生成有較強規律性的數據序列，然后建立相應的微 分方程模型，從而預測事物未來發展趨勢的狀況。其用等時距觀測到的反應預測 對象特征的一系列數量值構造灰色預測模型，預測未來某一時刻的特征量，或達到某一特征量的時間。

步驟一：生成數列

通過對原始數據的整理尋找數的規律，分為三類：

1.累加生成：?通過數列間各時刻數據的依個累加得到新的數據與數列，累加

前數列為原始數列，累加后為生成數列。

2.累減生成：?前后兩個數據之差，累加生成的逆運算，累減生成可將累加生

成還原成非生成數列。

3.映射生成：?累加、累減以外的生成方式。

步驟二：建立模型

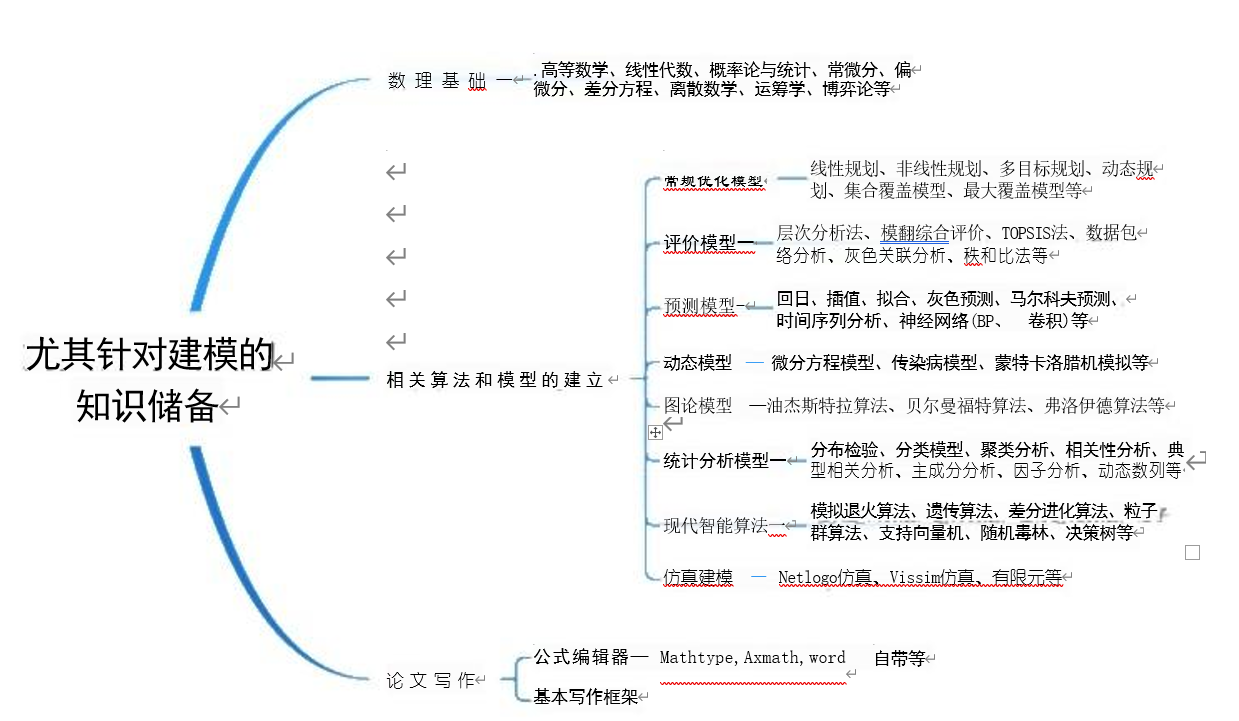
其中，關于相關算法和模型的學習，推薦選擇清風老師的課程，其課程性價 比高，講解系統透徹，基本涵括上述腦圖。智能算法可參考學習龔飛老師在我要 自學網中發布的課程《 Matlab2016? 數值計算與智能算法》,涵括大量智能算法 視頻教程。同時可以結合一些經典教材，如司守奎老師所寫 的《數學建模算法與程序》等。在學習的過程中， 一定要做到勤學勤練，只要練好了知識才是自己的!

另外提前準備好查找文獻的期刊網入口，無論是中文的知網、維普，還是英 文的 SCI 、Springer???? 等都要提前找到， 一般學校的圖書館都會有，沒有的話問其他學校同學借圖書館賬號或是找代理，總之不要影響比賽時查找文獻。關于文獻搜索，三個人要分工，即根據題目中可能涉及到的知識分頭尋找。

一般先找中文資料，在知網、維普、萬方等數據庫上進行搜索。建議把一個數據庫上關于這方面資料近10年所有相關論文都下載下來，然后用瀏覽的方式看完，有了一定的了解后選擇其中適合的方法加以改進創新，完成模型的建立。閱讀完中文文獻后可以開始搜索英文文獻，根據題目中的關鍵詞及近義詞進 行搜索。另外可以按照參考文獻歷程搜索，每篇文獻后面都列有相關的參考文獻， 可以通過尋找這些文獻來理解研究歷程，很可能就有新的發現。查找到文獻后，要注意整理與歸類，方便尋找與最后的記錄。