104.二叉樹的最大深度

給定一個二叉樹 root ，返回其最大深度。
二叉樹的 最大深度 是指從根節點到最遠葉子節點的最長路徑上的節點數。

思路1 迭代法 層序遍歷

層序遍歷的思路很簡單，其結果本來就是按層數記錄的，只需返回結果的長度皆可。

class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:if root ==None:return 0queue = collections.deque([root])levels = []while queue:for _ in range(len(queue)):level = []node = queue.popleft()level.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)levels.append(level)return len(levels)

思路2 遞歸法 前序/后序遍歷

二叉樹節點的深度：指從根節點到該節點的最長簡單路徑邊的條數或者節點數（取決于深度從0開始還是從1開始）
二叉樹節點的高度：指從該節點到葉子節點的最長簡單路徑邊的條數或者節點數（取決于高度從0開始還是從1開始）
使用前序（中左右）求的就是深度，使用后序（左右中）求的是高度。
根節點的高度就是二叉樹的最大深度

class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:return self.getdepth(root)def getdepth(self,node):if node == None:return 0leftdepth = self.getdepth(node.left)rightdepth = self.getdepth(node.right)depth = 1 + max(leftdepth,rightdepth)return depth

111.二叉樹的最小深度

給定一個二叉樹，找出其最小深度。
最小深度是從根節點到最近葉子節點的最短路徑上的節點數量。

思路1 層序遍歷

一層層遍歷過去，當有節點沒有子節點時返回當前層數.

class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:if root == None:return 0queue = collections.deque([root])cnt = 1while queue:for _ in range(len(queue)):        node = queue.popleft()if node.left==None and node.right==None:return cntelse:if node.left:queue.append(node.left)if node.right:queue.append(node.right)cnt += 1

思路2 后序遍歷

如果左子樹空，右子樹不空，則最小深度時1+右子樹深度
如果右子樹空，左子樹不空，則最小深度時1+左子樹深度
如果都不空，則最小深度為左右子樹深度最小值+1

class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:return self.getdepth(root)def getdepth(self,node):if node == None:return 0leftdepth = self.getdepth(node.left)rightdepth = self.getdepth(node.right)if node.left == None and node.right != None:return rightdepth + 1if node.left != None and node.right == None:return leftdepth + 1res = 1 + min(leftdepth,rightdepth)return res

222. 完全二叉樹的節點個數

力扣鏈接
給你一棵 完全二叉樹 的根節點 root ，求出該樹的節點個數。完全二叉樹 的定義如下：在完全二叉樹中，除了最底層節點可能沒填滿外，其余每層節點數都達到最大值，并且最下面一層的節點都集中在該層最左邊的若干位置。

思路1 層序遍歷

層序遍歷完之后統計里面的元素個數

class Solution:def countNodes(self, root: Optional[TreeNode]) -> int:if root == None:return 0levels = []self.helper(root, 0, levels)cnt = 0for level in levels:for _ in level:cnt += 1return cntdef helper(self, node, level, levels):if node == None:returnif len(levels)==level:levels.append([])levels[level].append(node.val)self.helper(node.left, level+1, levels)self.helper(node.right, level +1, levels)

思路2 完全二叉樹

完全二叉樹只有兩種情況，情況一：就是滿二叉樹，情況二：最后一層葉子節點沒有滿。

對于情況一，可以直接用 2^樹深度 - 1 來計算，注意這里根節點深度為1。

對于情況二，分別遞歸左孩子，和右孩子，遞歸到某一深度一定會有左孩子或者右孩子為滿二叉樹，然后依然可以按照情況1來計算。

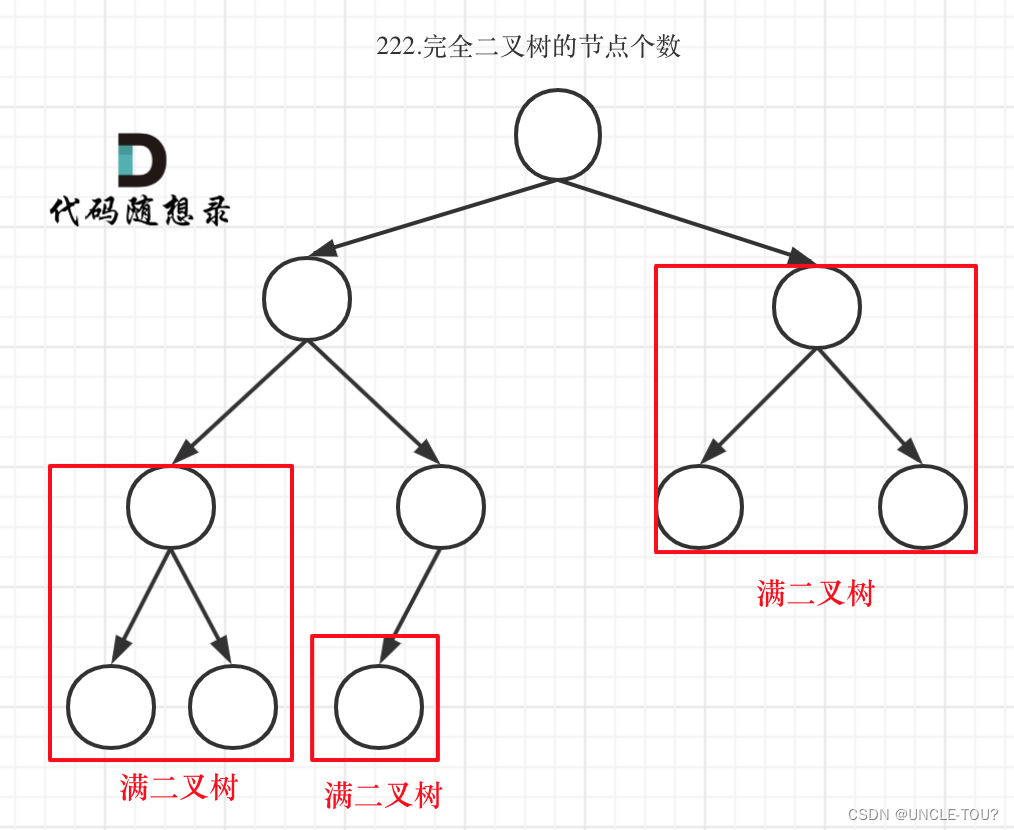
如何判斷是否滿二叉樹？在完全二叉樹中，如果向左遍歷的深度等于向右遍歷的深度，則說明為滿二叉樹（因為完全二叉樹如果不滿，則一定是右邊缺了）

class Solution:def countNodes(self, root: Optional[TreeNode]) -> int:return self.getnodenum(root)def getnodenum(self,node):if node == None:return 0leftnum = self.getnodenum(node.left)rightnum = self.getnodenum(node.right)treenum = 1+leftnum+rightnumreturn treenum