在深度學習的浩瀚世界中，代價函數（Cost Function），又稱損失函數（Loss Function）或目標函數（Objective Function），扮演著至關重要的角色，它就像一個導航員，為神經網絡的訓練指引方向。簡單來說，代價函數就是用來衡量模型預測結果與真實值之間差異的度量標準。這個差異越小，說明模型的性能越好。

核心作用：衡量與優化

代價函數的核心意義在于將模型的性能量化為一個單一的數值。這個數值就是我們進行優化的目標。在訓練過程中，我們不斷調整模型的參數（如權重和偏置），目的就是為了最小化這個代價函數的值。這個過程就像登山者朝著山谷最低點前進，每走一步都選擇能讓海拔降低的方向。

通過最小化代價函數，我們能有效地：

• 量化誤差：將復雜的預測結果與真實標簽之間的差距，簡化為一個易于計算和比較的數值。
• 指導優化：這個數值成為了梯度下降等優化算法的依據。梯度下降算法會計算代價函數對每個參數的梯度，并沿著梯度減小的方向更新參數，從而逐步減小誤差。
• 評估模型性能：代價函數的值可以作為模型在訓練集或驗證集上性能的一個重要指標。

常見的代價函數類型

不同的任務需要不同的代價函數來衡量誤差。以下是一些最常見且重要的代價函數：

a. 均方誤差 (MSE)

• 全稱：Mean Squared Error

• 公式：

  

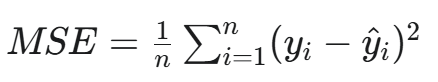
• 用途：主要用于回歸任務。它計算預測值和真實值之差的平方的平均值。

• 特點：對離群點（Outliers）非常敏感。由于平方運算，大的誤差會被放大，這使得模型會更努力地去糾正那些偏差較大的預測。

b. 交叉熵 (Cross-Entropy)

• 全稱：Cross-Entropy
• 用途：主要用于分類任務。它衡量兩個概率分布之間的差異，即模型預測的概率分布與真實標簽的概率分布之間的相似性。
• 特點：
  • 二元交叉熵：用于二分類任務，如邏輯回歸。
  • 多類別交叉熵：用于多分類任務，常與Softmax函數結合使用。
  • 相比于均方誤差，交叉熵在分類任務中表現更好。當預測結果與真實標簽相差甚遠時，交叉熵的梯度更大，能更快地進行參數更新。

c. 均方根誤差 (RMSE)

• 全稱：Root Mean Squared Error

• 公式：

  

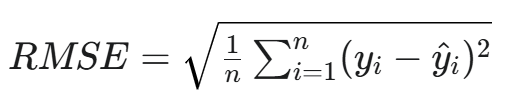
• 用途：同樣用于回歸任務。它是MSE的平方根。

• 特點：與原始數據的單位保持一致，更具可解釋性。

d. 平均絕對誤差 (MAE)

• 全稱：Mean Absolute Error

• 公式：

  

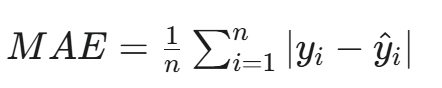
• 用途：用于回歸任務。

• 特點：對離群點不那么敏感，因為它是取絕對值而不是平方。當數據中存在較多異常值時，MAE是一個更穩健的選擇。

代價函數的選擇與影響

選擇合適的代價函數并非易事，它直接影響著模型的學習效果和最終性能。

• 任務決定選擇：正如前面所提到的，回歸問題通常使用MSE或MAE，而分類問題則首選交叉熵。
• 影響優化效率：一個設計良好的代價函數，其曲面（Cost Surface）應該是平滑且凸的（至少在局部），這樣才能讓梯度下降等優化算法更高效地找到最小值。如果代價函數存在很多局部最小值或平坦區域，優化過程可能會陷入困境。
• 模型泛化能力：有時，我們會將正則化項（如L1或L2正則化）添加到代價函數中，以懲罰復雜的模型，防止過擬合，從而提高模型的泛化能力。

總結：代價函數的重要性

總而言之，代價函數是深度學習的靈魂之一。它不僅僅是一個簡單的公式，更是連接模型、數據和優化算法的核心紐帶。它清晰地定義了“好”與“壞”，并為模型提供了一個明確的優化目標。沒有代價函數，模型的訓練將失去方向，無法從數據中學習有效的模式。理解和選擇正確的代價函數，是構建高效、穩健的深度學習模型的關鍵第一步。