支持向量機：從理論到實踐

一。理論概述

支持向量機（Support Vector Machine, SVM）是機器學習中最強大和最廣泛使用的算法之一，尤其在小樣本、高維數據的分類任務中表現出色。其核心思想基于統計學習理論中的結構風險最小化原則，通過構建最大間隔超平面來實現分類任務。本文將從數學基礎到實際應用，全面深入地解析SVM的工作原理和實現細節。

1. 線性可分支持向量機

1.1 基本概念與數學形式

對于完全線性可分的數據集，存在無數個超平面能夠將兩類樣本完全分開。SVM通過間隔最大化原則從中選擇唯一的最優超平面，該超平面不僅能夠正確分類所有訓練樣本，而且具有最好的泛化能力。

超平面的數學表示為：
$$w^{T}x+b=0$$
其中$w\in {\mathbb{R}}^n$是超平面的法向量，決定了超平面的方向；$b\in \mathbb{R}$是位移項，決定了超平面與原點的距離。

樣本點$x_i$到超平面的幾何距離為：
$$d_i=\frac{|w^T{x}_i+b|}{\Vert w\Vert }$$

1.2 函數間隔與幾何間隔

函數間隔的概念引入了類別信息：
$${\hat{\gamma }}_i=y_i(w^T{x}_i+b)$$
其中yi∈{?1,1}y_i \in \{-1, 1\}yi?∈{?1,1}是樣本的類別標簽。函數間隔的符號表示分類的正確性，絕對值表示分類的確信度。

整個數據集的函數間隔定義為所有樣本中函數間隔的最小值：
$$\hat{\gamma }=\underset{i=1,\dots ,N}{\min }{\hat{\gamma }}_i$$

然而，函數間隔存在一個顯著問題：對$w$和$b$進行等比例縮放時，超平面不變但函數間隔會改變。為解決這個問題，我們引入幾何間隔：

$${\gamma }_i=\frac{{\hat{\gamma }}_i}{\Vert w\Vert }=\frac{y_i(w^T{x}_i+b)}{\Vert w\Vert }$$

幾何間隔表示樣本點到超平面的真實歐幾里得距離，具有縮放不變性，能夠真實反映分類的確信度。

1.3 間隔最大化與優化問題

SVM的核心目標是找到最大幾何間隔的超平面，這可以表述為以下優化問題：

$$\underset{w,b}{\max }\gamma$$
$$\text{s.t.?}\frac{y_i(w^T{x}_i+b)}{\Vert w\Vert }\ge \gamma ,i=1,\dots ,N$$

通過令$\hat{\gamma }=1$（這可以通過調整$w$和$b$的尺度實現），問題轉化為等價的約束優化問題：

$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2$$
$$\text{s.t.?}{y}_i(w^T{x}_i+b)\ge 1,i=1,\dots ,N$$

這是一個典型的凸二次規劃問題，具有全局最優解。目標函數中的$\frac{1}{2}$是為了后續求導方便而添加的系數，不影響優化結果。

1.4 拉格朗日對偶理論與求解

應用拉格朗日乘子法，我們引入拉格朗日乘子${\alpha }_i\ge 0$，構造拉格朗日函數：

$$L(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2?\sum _{i=1}^N{\alpha }_i[y_i(w^T{x}_i+b)?1]$$

根據KKT條件，原問題的最優解滿足：

$${?}_{w}L=w?\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0$$
$$\frac{?L}{?b}=?\sum _{i=1}^N{\alpha }_i{y}_i=0$$
$${\alpha }_i[y_i(w^T{x}_i+b)?1]=0,i=1,\dots ,N$$

代入拉格朗日函數，得到對偶問題：

$$\underset{\alpha }{\max }?\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\alpha }_i$$
$$\text{s.t.?}{\alpha }_i\ge 0,\sum _{i=1}^N{\alpha }_i{y}_i=0$$

1.5 支持向量與決策函數

從KKT條件中的互補松弛條件${\alpha }_i[y_i(w^T{x}_i+b)?1]=0$可知：

• 當${\alpha }_i=0$時，對應樣本不是支持向量，對決策邊界沒有影響
• 當${\alpha }_i>0$時，必有$y_i(w^T{x}_i+b)=1$，對應樣本是支持向量

支持向量是位于間隔邊界上的樣本點，它們決定了最終的超平面。這一特性使得SVM的解具有稀疏性，僅依賴于少數支持向量。

最終的決策函數為：
$$f(x)=\text{sign}\left(\sum _{i=1}^N{\alpha }_i{y}_i{x}_i^{T}x+b\right)$$

其中$b$可以通過任意支持向量計算得到：$b=y_i?w^T{x}_i$（對于滿足$0<{\alpha }_i$的樣本）。

---

2. 近似線性可分數據（軟間隔SVM）

2.1 松弛變量與軟間隔概念

在實際應用中，數據很少是完美線性可分的，可能存在噪聲或異常點。軟間隔SVM通過引入松弛變量${\xi }_i\ge 0$，允許一些樣本被錯誤分類，從而提高模型的魯棒性。

優化問題變為：
$$\underset{w,b,\xi }{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i$$
$$\text{s.t.?}{y}_i(w^T{x}_i+b)\ge 1?{\xi }_i,{\xi }_i\ge 0,i=1,\dots ,N$$

其中$C>0$是正則化參數，控制誤分類懲罰與間隔大小之間的平衡：

• $C$值較大時，誤分類懲罰重，間隔較小，可能過擬合
• $C$值較小時，誤分類懲罰輕，間隔較大，可能欠擬合

2.2 軟間隔的對偶問題與支持向量分類

軟間隔SVM的對偶問題與硬間隔形式相似：

$$\underset{\alpha }{\max }?\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\alpha }_i$$
$$\text{s.t.?}0\le {\alpha }_i\le C,\sum _{i=1}^N{\alpha }_i{y}_i=0$$

KKT條件擴展為：
$${\alpha }_i[y_i(w^T{x}_i+b)?1+{\xi }_i]=0$$
$$(C?{\alpha }_i){\xi }_i=0$$

支持向量分為三類：

1. ${\alpha }_i=0$：正確分類的非支持向量，對決策邊界沒有影響
2. $0<{\alpha }_i<C$：位于間隔邊界上的支持向量，滿足$y_i(w^T{x}_i+b)=1$
3. ${\alpha }_i=C$：被錯誤分類的支持向量或落在間隔內的樣本，滿足${\xi }_i>0$

---

3. 非線性支持向量機與核方法

3.1 核技巧的數學原理

當數據在原始特征空間中線性不可分時，可以通過非線性映射$?:{\mathbb{R}}^d\to \mathcal{H}$將數據映射到高維特征空間$\mathcal{H}$，在其中數據變得線性可分。

在高維空間中的優化問題變為：
$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i$$
$$\text{s.t.?}{y}_i(w^T?(x_i)+b)\ge 1?{\xi }_i,{\xi }_i\ge 0$$

對偶問題為：
$$\underset{\alpha }{\max }?\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j?(x_i{)}^T?(x_j)+\sum _{i=1}^N{\alpha }_i$$

直接計算$?(x_i{)}^T?(x_j)$可能非常困難（甚至不可能），因此引入核函數：
$$K(x_i,x_j)=?(x_i{)}^T?(x_j)$$

3.2 常用核函數及其特性

1. 線性核：$K(x_i,x_j)=x_i^T{x}_j$

   • 參數少，速度快，適用于線性可分情況
   • 簡單，可解釋性強

2. 多項式核：$K(x_i,x_j)=(x_i^T{x}_j+c{)}^d$

   • 參數$d$控制映射后的空間維度
   • 當$d$較大時計算可能不穩定

3. 高斯徑向基核（RBF）：$K(x_i,x_j)=\exp (?\gamma \Vert x_i?x_j{\Vert }^2)$

   • 應用最廣泛的核函數，具有很強的非線性映射能力
   • 參數$\gamma$控制高斯函數的寬度，影響模型的復雜度

4. Sigmoid核：$K(x_i,x_j)=\tanh (\kappa x_i^T{x}_j+\theta )$

   • 來源于神經網絡理論，在某些特定問題上表現良好
   • 不是對所有參數都滿足Mercer條件

3.3 核函數的選擇與模型選擇

核函數的選擇依賴于具體問題和數據特性：

• 文本分類：通常使用線性核，因為文本數據往往已經是高維的
• 圖像識別：常用RBF核或多項式核，可以捕捉像素間的復雜關系
• 生物信息學：RBF核表現優異，適用于基因序列等復雜數據

模型選擇涉及參數調優，常用交叉驗證來確定最優的$C$和核參數（如RBF核的$\gamma$）。

3.4 Mercer定理與核函數有效性

核函數必須滿足Mercer條件：對任意函數$g(x)$滿足$\int g(x{)}^{2}dx<\infty$，有：
$$?K(x,y)g(x)g(y)dxdy\ge 0$$

這保證了核矩陣$K=[K(x_i,x_j)]$是半正定的，對應的優化問題是凸的，有全局最優解。

---

4. 支持向量機的擴展與變體

4.1 支持向量回歸（SVR）

支持向量機也可以用于回歸任務，稱為支持向量回歸。其基本思想是：尋找一個函數$f(x)=w^T?(x)+b$，使得$f(x)$與$y$的偏差不超過$?$，同時保持函數盡量平坦。

優化問題為：
$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N({\xi }_i+{\xi }_i^{?})$$
$$\text{s.t.?}?\begin{array}{l}{y}_i?w^T?(x_i)?b\le ?+{\xi }_i\\ w^T?(x_i)+b?y_i\le ?+{\xi }_i^{?}\\ {\xi }_i,{\xi }_i^{?}\ge 0\end{array}$$

4.2 多類支持向量機

SVM本質上是二分類器，擴展多類分類的方法主要有：

1. 一對多（One-vs-Rest）：為每個類別訓練一個二分類器
2. 一對一（One-vs-One）：為每兩個類別訓練一個二分類器
3. 多類SVM：直接修改優化目標，考慮所有類別

4.3 結構化SVM

用于結構化輸出問題，如序列標注、解析樹構建等，通過定義適當的損失函數和特征映射來處理復雜的輸出結構。

---

5. 支持向量機的實踐考慮

5.1 數據預處理與特征縮放

SVM對數據縮放敏感，特別是使用基于距離的核函數（如RBF核）時。常見的預處理方法：

• 標準化：將特征縮放到均值為0，方差為1
• 歸一化：將特征縮放到[0,1]或[-1,1]區間

5.2 計算效率與大規模數據處理

傳統SVM訓練算法的時間復雜度約為$O(n^3)$，空間復雜度約為$O(n^2)$，難以處理大規模數據集。改進方法包括：

• 分解算法（如SMO）
• 隨機梯度下降
• 近似核方法
• 分布式計算

5.3 模型解釋性與特征重要性

雖然核SVM具有良好的分類性能，但模型解釋性較差。提高解釋性的方法：

• 使用線性核或可解釋性強的核函數
• 分析支持向量的權重
• 使用模型無關的解釋方法（如LIME、SHAP）

6. 支持向量機的局限性與挑戰

• 計算復雜度：對于大規模數據集，訓練時間較長，內存消耗大，限制了其在實際中的應用。
• 核函數選擇：核函數及其參數的選擇很大程度上依賴于經驗和實驗，缺乏系統的理論指導。
• 概率輸出：標準SVM不直接提供概率輸出，需要通過 Platt scaling 等額外方法進行校準。
• 多類分類：SVM本質上是二分類器，多類擴展需要額外的策略，增加了復雜性。

---

二。SVM模型應用于人臉分類

1. 數據加載與預處理

from time import timeimport matplotlib.pyplot as plt
from scipy.stats import loguniformfrom sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
from sklearn.metrics import ConfusionMatrixDisplay, classification_report
from sklearn.model_selection import RandomizedSearchCV, train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

people_faces = fetch_lfw_peopletch()
# 從 LFW（Labeled Faces in the Wild）數據集中下載人臉圖片
# min_faces_per_person=70 → 只保留至少有 70 張照片的人物
# resize=0.4 → 將圖片縮小到原來的 40%，降低計算量
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)# 獲取數據集的基本形狀信息
n_samples, h, w = lfw_people.images.shape  # 樣本數、高度、寬度# 機器學習使用拉平后的像素數據（忽略像素的空間位置信息）
X = lfw_people.data  # 每張圖片展平成一維向量
n_features = X.shape[1]  # 特征數（像素個數）# 標簽（人物 ID）
y = lfw_people.target
target_names = lfw_people.target_names  # 人物姓名
n_classes = target_names.shape[0]  # 類別數# 打印數據集大小信息
print("Total dataset size:")
print("n_samples: %d" % n_samples)
print("n_features: %d" % n_features)
print("n_classes: %d" % n_classes)結果：
Total dataset size:
n_samples: 1288
n_features: 1850
n_classes: 7

從LFW（Labeled Faces in the Wild）數據集中加載人臉圖像數據，并進行初步預處理。通過設置min_faces_per_person=70篩選出至少有70張圖像的人物，確保每個類別有足夠的樣本；resize=0.4將圖像縮小到原尺寸的40%，顯著降低計算復雜度。隨后，將圖像數據展平為一維向量作為特征，提取對應的類別標簽和人物名稱，輸出數據集的基本統計信息（樣本數、特征維度和類別數）

2. 訓練測試劃分與數據標準化

# 劃分訓練集和測試集，比例 70% 訓練 / 30% 測試
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=2025
)# 數據標準化（均值為 0，方差為 1），有助于加快收斂并提升模型性能
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)  # 用訓練集擬合并轉換
X_test = scaler.transform(X_test)        # 用相同參數轉換測試集

將數據集按7:3比例劃分為訓練集和測試集。采用StandardScaler對數據進行標準化處理，使每個特征的均值為0、方差為1。這一步驟至關重要，因為SVM對特征尺度敏感，標準化可以加速模型收斂并提升性能。注意測試集使用訓練集擬合的縮放參數進行轉換，避免數據泄露。

3. 主成分分析（PCA）降維

# 設定 PCA 要保留的主成分個數，這里是 100 個
n_components = 100# 記錄開始時間，用于計算運行耗時
start = time()# 創建 PCA 對象并擬合訓練數據
# 參數解釋：
#   n_components=n_components  -> 保留的主成分數量
#   svd_solver="randomized"    -> 使用隨機化 SVD 算法，加速計算（適合高維數據）
#   whiten=True                -> 白化處理，使得每個主成分的方差為 1（有助于后續分類器性能）
# .fit(X_train) -> 在訓練集上擬合 PCA 模型，學習主成分方向
pca = PCA(n_components=n_components, svd_solver="randomized", whiten=True).fit(X_train)# 獲取 PCA 學到的主成分（特征向量），并將它們還原成 h×w 的二維圖像
# 這些主成分在臉部識別領域被稱為 "eigenfaces"（特征臉）
eigenfaces = pca.components_.reshape((n_components, h, w))# 記錄結束時間
end = time()# 使用訓練好的 PCA 模型將訓練集投影到主成分空間
# 得到的 X_train_pca 是降維后的特征表示
X_train_pca = pca.transform(X_train)# 同樣地，將測試集投影到主成分空間
X_test_pca = pca.transform(X_test)# 輸出整個 PCA 特征提取過程的耗時
print("finished in %0.3fs" % (end - start))

使用PCA對高維圖像特征進行降維，保留100個主要成分。設置whiten=True對主成分進行白化處理，使各維度方差歸一化，有助于提升后續分類器性能。采用隨機化SVD算法（svd_solver="randomized"）提高計算效率。降維后將訓練集和測試集分別投影到主成分空間，得到低維特征表示（X_train_pca和X_test_pca），同時提取特征臉（eigenfaces）用于可視化。

4. 支持向量機超參數優化

# 記錄開始時間
start = time()# 定義超參數搜索范圍 param_grid
# 這里使用的是 loguniform 分布（對數均勻分布），適合搜索跨度很大的超參數
#  - "C" 是 SVM 的正則化參數，控制分類器對訓練集的擬合程度
#  - "gamma" 是 RBF 核函數的核寬度參數，影響單個樣本的影響范圍
#    范圍：
#      C: 從 1e3 到 1e5
#      gamma: 從 1e-4 到 1e-1
param_grid = {"C": loguniform(1e3, 1e5),"gamma": loguniform(1e-4, 1e-1),
}# 創建一個隨機搜索交叉驗證器 RandomizedSearchCV
#  - SVC(kernel="rbf", class_weight="balanced") ：使用 RBF 核的支持向量機，類別權重平衡處理
#  - param_distributions=param_grid ：指定要搜索的參數分布
#  - n_iter=10 ：隨機采樣 10 組參數組合進行測試
clf = RandomizedSearchCV(SVC(kernel="rbf", class_weight="balanced"), param_grid, n_iter=10
)# 在訓練集（PCA 降維后的特征）上擬合模型并進行超參數搜索
#  X_train_pca：降維后的訓練數據
#  y_train：對應的標簽
clf = clf.fit(X_train_pca, y_train)# 輸出搜索過程耗時
print("finished in %0.3f" % (time() - start))# 輸出搜索得到的最優模型（包含最佳參數 C 和 gamma）
print(clf.best_estimator_)

使用隨機搜索（RandomizedSearchCV）優化SVM的超參數（正則化參數C和RBF核參數gamma）。參數搜索范圍設置為對數均勻分布（loguniform），涵蓋合理的數值區間。采用帶類別權重平衡（class_weight="balanced"）的RBF核SVM，以處理類別樣本量不均衡的問題。通過10次參數采樣和交叉驗證，尋找最優超參數組合。

5. 模型預測與評估

# 記錄開始時間
start = time()# 使用訓練好的分類器（clf）對測試集特征進行預測
#  X_test_pca 是經過 PCA 降維的測試集數據
#  y_pred 是預測得到的標簽
y_pred = clf.predict(X_test_pca)# 輸出預測過程耗時
print("finished in %0.3fs" % (time() - start))# 打印分類性能評估報告
# classification_report 會輸出：
#   - precision（精確率）
#   - recall（召回率）
#   - f1-score（F1 分數）
#   - support（每個類別的樣本數量）
# target_names 用于顯示每個類別的真實名稱（這里是人物姓名）
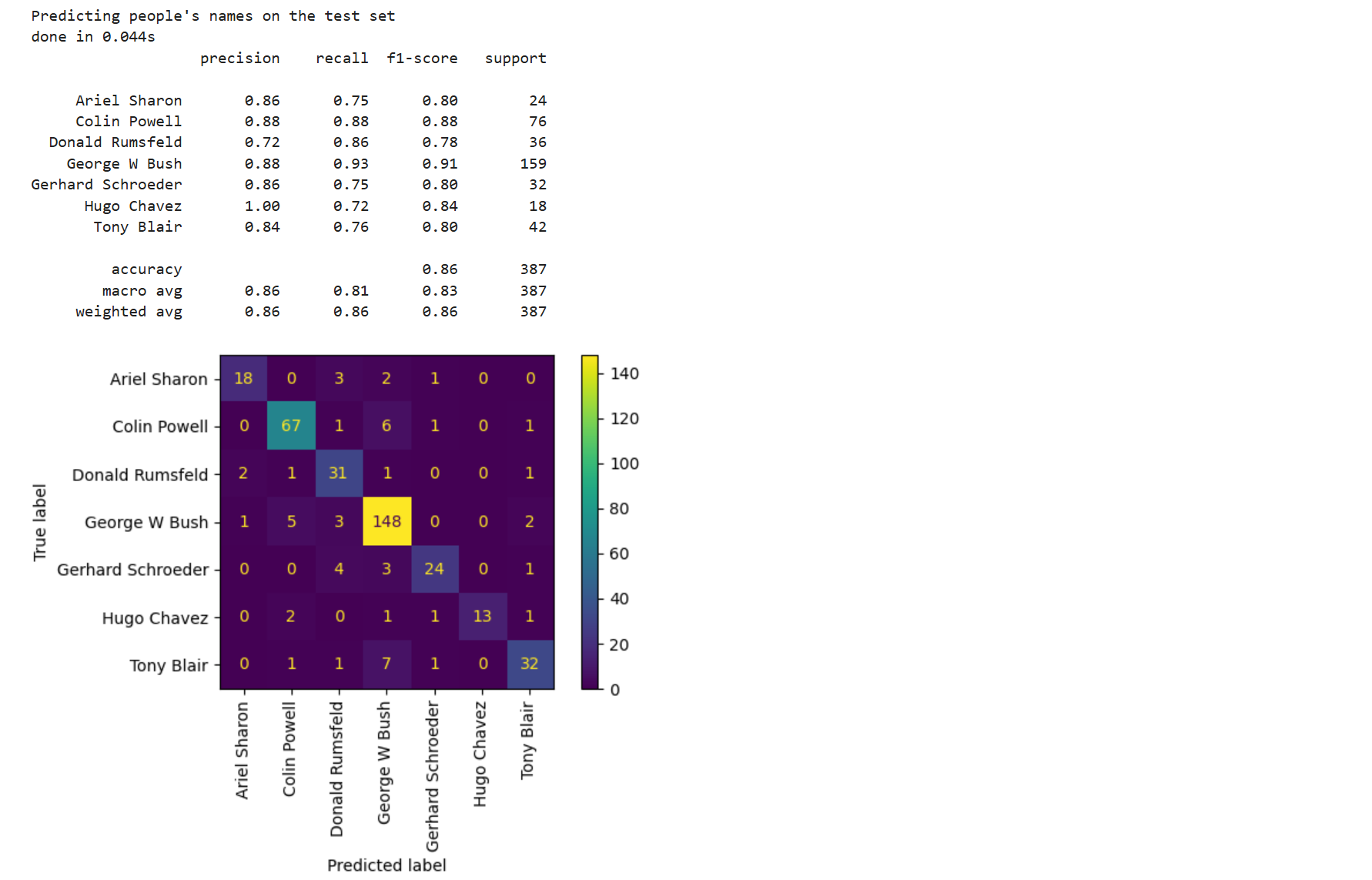
print(classification_report(y_test, y_pred, target_names=target_names))# 繪制混淆矩陣（Confusion Matrix）
# ConfusionMatrixDisplay.from_estimator 會：
#   - 用分類器 clf
#   - 輸入測試集數據和真實標簽
#   - 自動計算混淆矩陣并繪制
# display_labels=target_names 用于顯示真實的類別名稱
# xticks_rotation="vertical" 讓橫軸標簽豎直顯示，防止文字重疊
ConfusionMatrixDisplay.from_estimator(clf, X_test_pca, y_test, display_labels=target_names, xticks_rotation="vertical"
)# 自動調整子圖布局，避免文字或圖像被遮擋
plt.tight_layout()# 顯示繪制好的混淆矩陣圖
plt.show()

使用優化后的SVM模型對測試集進行預測，并輸出詳細分類報告（包括精確率、召回率、F1分數等指標）和混淆矩陣。混淆矩陣可視化展示了各類別的分類情況。

6. 預測結果標題生成與可視化

import matplotlib.pyplot as pltdef plot_gallery(images, titles, h, w, n_row=4, n_col=4):"""繪制圖像網格（gallery）"""fig, axes = plt.subplots(n_row, n_col, figsize=(1.8 * n_col, 2.4 * n_row))  # 創建子圖axes = axes.flatten()  # 展平成一維，方便索引for i in range(n_row * n_col):axes[i].imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)  # 顯示灰度圖axes[i].set_title(titles[i], size=12)  # 設置標題axes[i].set_xticks([])  # 去掉橫坐標刻度axes[i].set_yticks([])  # 去掉縱坐標刻度plt.tight_layout()  # 自動調整布局plt.show()

定義plot_gallery函數，用于以網格形式展示多張圖像。函數接受圖像數據、標題列表和圖像尺寸參數，自動創建子圖布局，顯示灰度圖像并設置標題。

def title(y_pred, y_test, target_names, i):"""生成第 i 張圖片的預測與真實標簽標題"""pred_name = target_names[y_pred[i]].rsplit(" ", 1)[-1]  # 預測姓名（取姓氏）true_name = target_names[y_test[i]].rsplit(" ", 1)[-1]  # 真實姓名（取姓氏）return "predicted: %s\ntrue:      %s" % (pred_name, true_name)# 生成預測結果標題列表
prediction_titles = [title(y_pred, y_test, target_names, i) for i in range(y_pred.shape[0])
]# 繪制測試集圖片及預測結果
plot_gallery(X_test, prediction_titles, h, w)

根據預測結果和真實標簽生成每張測試圖像的標題，格式為“預測姓名/真實姓名”。僅使用人物姓氏（通過rsplit提取）簡化顯示。

7. 特征臉可視化

# 生成特征臉（Eigenfaces）標題
eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])]# 繪制特征臉
plot_gallery(eigenfaces, eigenface_titles, h, w)plt.show()

調用plot_gallery函數可視化PCA提取的前100個特征臉。特征臉反映了人臉圖像的主要變化模式，是PCA降維的基礎。