深度學習周報（9.8~9.14）

摘要

Abstract

1 LSTM相關網絡總結與對比

1.1 理論總結

1.2 代碼運行對比

2 量子計算入門

3 總結

摘要

本周首先總結了LSTM、Bi-LSTM與GRU的區別與優缺點，對比了三者實戰的代碼與效果，還另外拓展了一些循環神經網絡變體（包括窺視孔LSTM、耦合門LSTM與SRU）。其次，初步了解了量子計算的相關知識，包括量子比特、量子糾纏、量子干涉等，學習了量子比特與經典比特的區別、量子計算的經典算法、面臨的挑戰、主流技術路線與部分應用場景。

Abstract

This week, I firstly summarized the differences, advantages, and disadvantages among LSTM, Bi-LSTM, and GRU, compared their practical code implementations and performances. Additionally, I explored several RNN variants, including Peephole LSTM, Coupled Gate LSTM, and SRU. Secondly, I gained preliminary knowledge of quantum computing, covering concepts such as qubits, quantum entanglement, and quantum interference. I also studied the distinctions between qubits and classical bits, classic quantum algorithms, current challenges, mainstream technological approaches, and some application scenarios.

1 LSTM相關網絡總結與對比

1.1 理論總結

回顧上周學習的LSTM、Bi-LSTM與GRU三種網絡結構。

LSTM主要引入細胞狀態與三個門控機制（遺忘門、輸入門與輸出門）以解決了傳統RNN的相關問題，例如梯度消失，它能捕捉長期依賴，適合處理長序列，但參數多，訓練十分緩慢；

Bi-LSTM沒有改動LSTM的結構，而是使用兩個獨立的LSTM結構分布從右到左和從左到右處理序列，對兩者結果進行求和或者拼接得到最終結果。因此，它的參數量相較LSTM更大，訓練更慢，同時它需要完整序列，無法進行實時預測類的任務。但它能夠捕捉語言語法中一些特定的前置或后置特征，增強語義關聯，結果更為精準；

GRU則對LSTM的結構進行了部分改動，將三個門控機制簡化合并到兩個（更新門與重置門），在簡化結構、減少參數量的同時略微削弱了其長期依賴建模的能力。在大多數任務中，GRU與LSTM性能還是接近的。

除此之外，循環神經網絡還有許多其他的變體，例如，窺視孔 LSTM（Peephole LSTM），它在標準 LSTM 基礎上，讓門控機制也能訪問細胞狀態?，能更精細地控制信息流動，主要應用在語音識別、手寫識別等需要精確時序控制的任務上；耦合門 LSTM（Coupled LSTM），它將遺忘門和輸入門耦合，不再獨立決定“忘記什么”和“記住什么”，而是統一決策，它強制忘記舊信息才能記住新信息，不夠靈活，故很少使用；還有SRU（Simple Recurrent Unit），它是一種高度并行化的循環神經網絡單元，由 Milly Song 等人在 2017 年提出，訓練速度極快（接近 CNN），顯存占用小且適合長文本、語音等任務，其關鍵在于將隱藏狀態的更新過程從時間依賴中解耦，允許完全并行計算整個序列，不像普通循環神經網絡那樣必須按時間步順序計算。

1.2 代碼運行對比

上周進行了LSTM的代碼實戰，訓練總共花費6小時33分鐘40秒，最終結果如下：

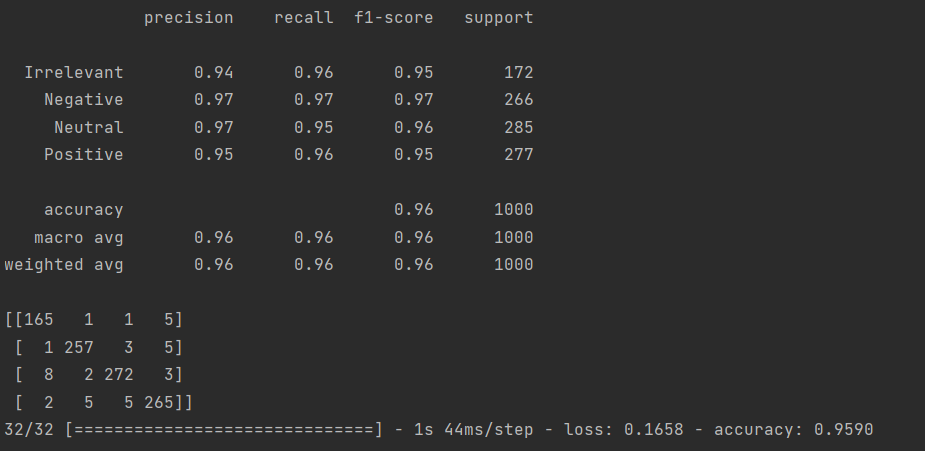
上述結果包括各項指標、混淆矩陣以及最終的損失與準確率。其中?macro avg 的中文名稱為宏平均，其計算方式為每個指標的算術平均。weighted avg 是加權平均，它的計算方式是用每一個類別樣本數量在所有類別的樣本總數的占比作為權重。

若利用Bi-LSTM進行訓練，需對模型定義部分進行如下改動：

def build_model(hp):model = Sequential([Embedding(input_dim=len(tokenizer.word_index) + 1, output_dim=100, input_length=MAX_SEQUENCE_LENGTH),#改動部分Bidirectional(LSTM(units=hp.Int('LSTM_UNITS', min_value=64, max_value=256, step=64),dropout=hp.Float('dropout_rate', min_value=0.2, max_value=0.5, step=0.1))),Dense(64, activation='relu'),Dropout(0.5),Dense(y_train.shape[1], activation='softmax')])model.compile(loss='categorical_crossentropy',optimizer=Adam(learning_rate=hp.Choice('learning_rate', values=[0.001, 0.0005, 0.0001])),metrics=['accuracy'])return model

主要是利用 Bidirectional 包裝器對 LSTM 層進行包裝，它會創建兩個獨立的 LSTM 層，一個按原始順序處理序列，一個按逆序處理序列，然后將兩者的輸出進行合并（默認是拼接 concat，也可以通過? merge_mode 進行調整）

訓練總共花費13小時7分鐘45秒，結果如下：

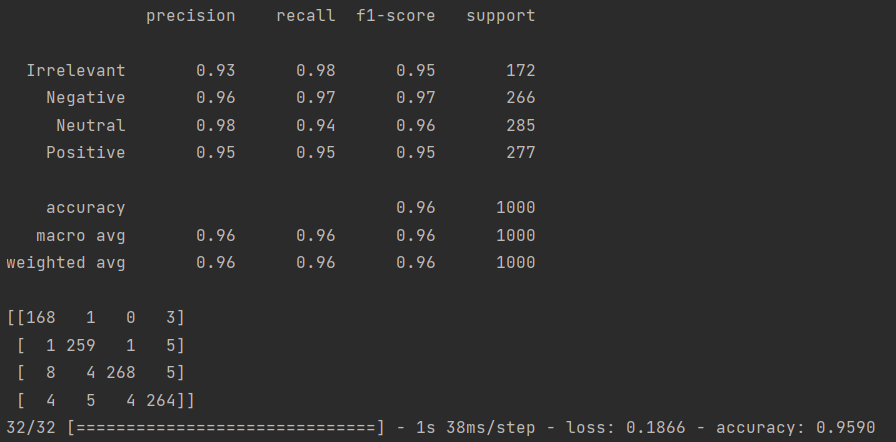
若利用GRU進行訓練，需對模型定義部分進行如下改動：

def build_model(hp):model = Sequential([Embedding(input_dim=len(tokenizer.word_index) + 1, output_dim=100, input_length=MAX_SEQUENCE_LENGTH),#改動部分GRU(units=hp.Int('GRU_UNITS', min_value=64, max_value=256, step=64),dropout=hp.Float('dropout_rate', min_value=0.2, max_value=0.5, step=0.1)),Dense(64, activation='relu'),Dropout(0.5),Dense(y_train.shape[1], activation='softmax')])model.compile(loss='categorical_crossentropy',optimizer=Adam(learning_rate=hp.Choice('learning_rate', values=[0.001, 0.0005, 0.0001])),metrics=['accuracy'])return model

主要是將原代碼中的?LSTM 改為 GRU。

訓練總共花費4小時8分鐘57秒，結果如下：

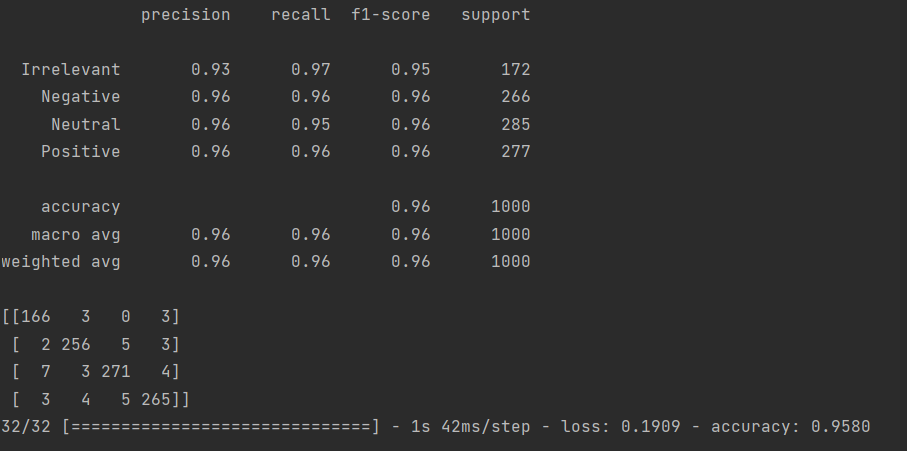
2 量子計算入門

量子計算本質上是一種新型的計算方式，它利用量子力學中的某些性質或現象（如疊加和糾纏），有望在特定任務上實現對經典計算機的“量子優越性”（Quantum Advantage），指的是量子計算機在解決某個特定、精心設計的問題上，其運算速度遠遠超過當今最強大的經典超級計算機，以至于經典計算機在可接受的時間內（例如數千年甚至更久）無法完成相同任務，這也是所謂的量子霸權。2019年，谷歌“懸鈴木”（Sycamore）處理器在200秒內完成了一項經典超算需一萬年才能完成的計算任務，首次實驗證明了量子優越性，標志著量子計算從理論走向實踐的關鍵里程碑。

為了理解量子計算，首先認識其最基本信息單元，量子比特（Qubit），它對應著經典計算中的比特。

經典計算中比特的狀態只能是?0?或?1，具有確定性，測量能夠得到真實值，而且多個比特若無邏輯鏈接，則狀態相互獨立；

但量子比特的狀態不僅可以是?|0?、|1?，還可以是兩者的疊加態，可表示為：

|ψ? = a|0?+b|1??

其中 a 和 b 是復數，稱為概率幅，且滿足?? $\left | a \right |^{2} + \left | b \right |^{2} =1$ ?。

量子比特的狀態在測量前處于不確定狀態，測量時會以?的概率坍縮為 |0? ，以? $\left | b \right |^{2}$ ?的概率坍縮為|1?，多個量子比特可形成糾纏態，狀態關聯強。

疊加態是量子并行性的基礎。一個n量子比特的系統可以同時表示2^n個經典狀態的疊加。例如，2個量子比特可以同時處于|00?、|01?、|10?、|11?四種狀態的疊加。這意味著量子計算機在一次操作中可以同時處理指數級數量的可能性，為解決復雜問題提供了巨大的潛在算力。

量子糾纏主要是指當兩個或多個量子比特發生糾纏時，它們的狀態會變得密不可分，無論相隔多遠，對其中一個量子比特的測量會瞬間決定其他糾纏量子比特的狀態。愛因斯坦曾稱其為“鬼魅般的超距作用”。糾纏是量子通信（如量子密鑰分發）、量子隱形傳態和許多量子算法的核心資源，它使得量子系統能夠表現出經典系統無法復制的強關聯性。

在此基礎上，量子計算可以通過精心設計的量子門操作（單量子比特門、雙量子比特門等）構成量子電路，利用量子干涉來增強正確答案的概率幅，同時抑制錯誤答案的概率幅。這類似于波的干涉現象，即相長干涉使波增強，相消干涉使波減弱。量子算法的精妙之處就在于如何編排量子門序列，使得計算路徑的干涉效應最終導向期望的輸出結果（使得其概率盡可能地大）。

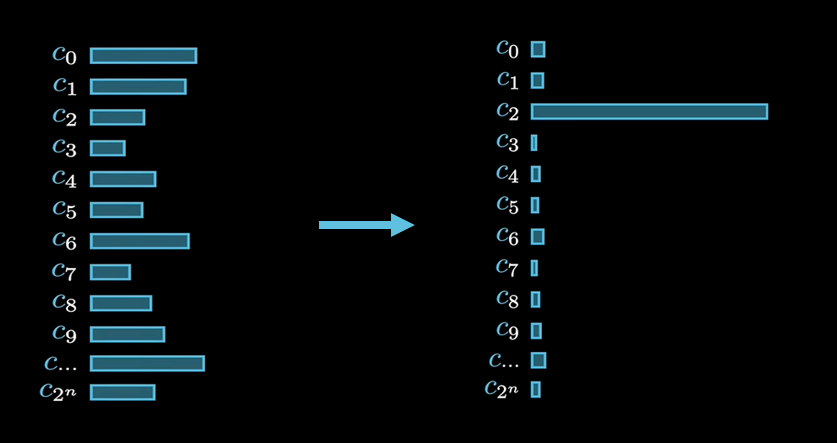
標志性量子算法包括以下幾種，在后續也會詳細學習：

首先是Shor算法，它由彼得·肖爾（Peter Shor）在1994年提出，主要解決了大整數質因數分解的問題。RSA等廣泛使用的公鑰加密體系的安全性都是基于大數分解的困難性。Shor算法能在多項式時間內解決此問題，一旦大規模容錯量子計算機實現，將對現有密碼學體系構成顛覆性威脅，這推動了“后量子密碼學”（PQC）的研究。

其次是Grover算法，由洛夫·格羅弗（Lov Grover）在1996年提出，主要解決了在無序數據庫中搜索特定項的問題。這個問題在經典計算中的時間復雜度為O(N)，平均檢查次數為? $\frac{N}{2}$ ?,而Grover算法僅需約?√N 次查詢時間復雜度為O(√N)時間，提供了二次加速。它雖然不如Shor算法的指數加速震撼，但在優化、密碼分析等領域仍有重要應用價值。

最后是量子變分算法（VQE, QAOA）。由于在當前含噪聲中等規模量子（NISQ）時代，硬件存在噪聲和錯誤，難以運行前面兩種或其他需要長深度電路和高保真度的“純”量子算法。量子變分算法混合量子計算與經典計算，利用量子處理器和經典優化器，對噪聲有一定容忍度，能利用現有NISQ硬件進行實驗。其中量子處理器執行一個參數化的淺層量子電路（變分電路），測量輸出；經典計算機根據測量結果優化電路參數，以最小化某個目標函數（如分子基態能量）。

量子計算的發展也面臨一些挑戰：

首先，由于量子態極其脆弱，易受環境噪聲（熱、電磁輻射等）干擾而逐步失去量子特性，退化為經典行為，保持量子態穩定的時間有限，這個退化的過程叫退相干，保持量子態穩定的時間被稱為相干時間。退相干是量子計算中必須克服的最根本、最頑固的障礙之一。

其次，為了克服噪聲，需引入冗余量子比特進行糾錯。主流方案如表面碼（Surface Code）要求大量物理量子比特來編碼一個邏輯量子比特（可能需數千甚至上萬），對硬件規模和保真度的要求極高。

還有是可擴展性，要制造、操控和連接成千上萬個高質量量子比特，并保持高保真度，也是工程上的巨大挑戰。

量子計算的主流技術路線包括超導量子比特（IBM, Google）、囚禁離子（IonQ）、光子量子計算（Xanadu）以及中性原子（ColdQuanta）。超導量子比特主要利用超導電路進行實現，制造工藝與半導體兼容，可擴展性好，但需極低溫稀釋制冷機，且易受電磁噪聲干擾；囚禁離子主要是利用電磁場囚禁單個離子，用激光操控其能級作為量子比特，它的相干時間長，量子門保真度高，比特間連接性好，但操控速度相對較慢，規模化集成難度大；光子量子計算主要是利用光子的路徑、偏振等來編碼量子信息，可以在室溫下運行，抗干擾能力強，天然適合量子通信，但實現確定性的相互作用較為困難，規模化挑戰大；中性原子主要就是利用光鑷陣列囚禁中性原子，用里德堡態實現長程相互作用，其可編程性強，易于構建二維/三維陣列，是近期發展迅速的熱門方向。不同技術路線各有優劣，在相干時間、操控精度、可擴展性等方面面臨不同挑戰。

量子計算并非萬能，它更擅長解決具有特定結構的問題，如：量子化學與材料科學，精確模擬分子和材料的量子行為，加速新藥、催化劑、電池材料的研發；優化問題，比如物流、金融投資組合、供應鏈管理中的復雜優化難題的解決；機器學習，開發量子機器學習算法，處理高維數據，加速訓練過程；密碼學，破解現有加密，同時推動量子安全加密技術的發展。