歸一化(Normalization)是一種將數據轉換到相同尺度的預處理技術,它通常用于讓不同特征(或數據項)具有相同的量綱或范圍。在聯邦學習中,歸一化可以用來處理非獨立同分布(Non-IID)**數據中的差異,確保不同客戶端的訓練過程具有可比性,從而有效地提高模型的穩定性和準確性。
1. 歸一化的基本概念
歸一化的目標是將數據縮放到特定的范圍內,常見的范圍是 [0, 1] 或 [-1, 1]。通過這種方式,可以消除數據中由于量綱差異或尺度差異帶來的影響,使得不同客戶端的梯度或損失值在同一個尺度上進行比較。
常用的歸一化方法有:
最小-最大歸一化(Min-Max Normalization):將數據縮放到指定的范圍(通常是 [0, 1])。
Z-score標準化(Z-score Normalization):通過數據的均值和標準差對數據進行標準化。
2. 最小-最大歸一化(Min-Max Normalization)
最小-最大歸一化是最常用的歸一化方法之一。它將數據按比例縮放到 [0, 1] 之間,公式如下:
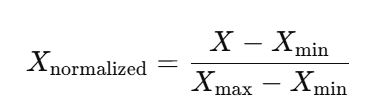
其中:
?是原始數據(例如,客戶端的損失值或梯度值)。
和
分別是數據中的最小值和最大值。
是歸一化后的數據。
例子解釋
假設5個客戶端的損失值如下:
| 客戶端 | 損失值 |
|---|---|
| A | 0.8 |
| B | 1.2 |
| C | 0.9 |
| D | 0.7 |
| E | 5.0 |
最小值(
) = 0.7
最大值(
) = 5.0
那么,歸一化后的損失值計算如下:
最終的歸一化損失值如下:
| 客戶端 | 原始損失值 | 歸一化后損失值 |
|---|---|---|
| A | 0.8 | 0.0233 |
| B | 1.2 | 0.1163 |
| C | 0.9 | 0.0465 |
| D | 0.7 | 0 |
| E | 5.0 | 1 |
通過歸一化方法,所有客戶端的損失值都被縮放到了相同的范圍內,便于進行比較。
3. Z-score標準化
Z-score標準化是另一種常見的數據歸一化方法,它將數據變換為均值為0、標準差為1的分布。公式如下:
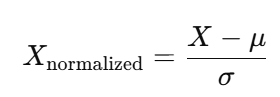
其中:
是原始數據(例如,客戶端的損失值或梯度值)。
是數據的均值(所有數據的平均值)。
是數據的標準差(數據的離散程度)。
例子解釋
假設使用上述的損失值(A: 0.8, B: 1.2, C: 0.9, D: 0.7, E: 5.0)。
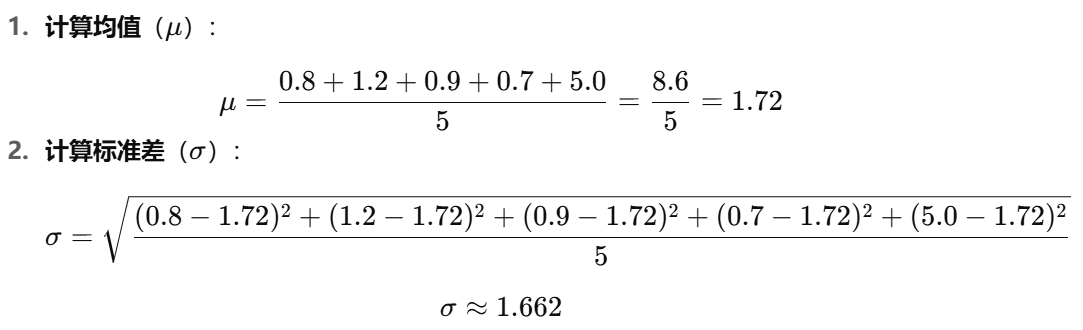
標準化后的值

最終的標準化結果:
| 客戶端 | 原始損失值 | 標準化后損失值 |
|---|---|---|
| A | 0.8 | -0.556 |
| B | 1.2 | -0.313 |
| C | 0.9 | -0.494 |
| D | 0.7 | -0.612 |
| E | 5.0 | 1.993 |
通過Z-score標準化后,所有客戶端的損失值以均值0、標準差1的方式呈現,避免了數據尺度對分析的影響。
4. 選擇哪種歸一化方法?
最小-最大歸一化:適用于你已知數據的范圍,并且希望將所有數據縮放到一個固定范圍內。通常用于算法對特定范圍敏感的情況,比如在神經網絡中,激活函數(如Sigmoid)通常對歸一化數據較為敏感。
Z-score標準化:適用于數據分布較為復雜,或者你不確定數據的范圍時。它不受到極端值的影響,適用于大多數基于距離的算法(如KNN、SVM等)和一些優化算法。







—stack和queue的介紹及使用)
)




![[C語言]常見排序算法①](http://pic.xiahunao.cn/[C語言]常見排序算法①)




)

