筆記用于個人復習和鞏固，題解非原創，參考LeetCode官方題解以及各個大佬的解法，希望給大家帶來幫助，同時筆記也能督促我學習進步

這周主要把滑動窗口和子串的題目刷了一遍

Week2

D1 滑動窗口

只有當數組中所有數都是非負數時，才能使用滑動窗口。

如果數組中包含負數不能使用標準的滑動窗口

滑動窗口的核心前提：

當窗口擴大時，和變大；窗口縮小時，和變小。

209. 長度最小的子數組

209. 長度最小的子數組

class Solution {public int minSubArrayLen(int target, int[] nums) {int n = nums.length;int ans = n + 1;int sum = 0;int left = 0;for(int right = 0;right < n;right++){sum += nums[right];while(sum >= target){ans = Math.min(ans,right - left + 1);sum -= nums[left];left++;}}return ans <= n ? ans : 0;}
}

713. 乘積小于 K 的子數組

713. 乘積小于 K 的子數組

class Solution {public int numSubarrayProductLessThanK(int[] nums, int k) {if(k <= 1){return 0;}int n = nums.length;int ans = 0;int prod = 1;int left = 0;for(int right = 0;right < n;right++){prod *= nums[right];while(prod >= k){ //不滿足要求prod /= nums[left];left++; //縮小窗口}ans += right - left + 1;}return ans;}
}

3. 無重復字符的最長子串

3. 無重復字符的最長子串

class Solution {public int lengthOfLongestSubstring(String S) {char[] s = S.toCharArray();int ans = 0;int n = s.length;int left = 0;int[] cnt = new int[128];for(int right = 0;right < n;right++){char c = s[right];cnt[c]++;while(cnt[c] > 1){ //窗口有重復字符cnt[s[left]]--;//移除窗口左端點字符left++;//縮小窗口}ans = Math.max(ans,right - left + 1);}return ans;}
}

D2 定長滑窗&不定長滑窗

定長滑窗

class Solution {public List<Integer> findAnagrams(String s, String p) {List<Integer> ans = new ArrayList<>();int n = s.length(); //測量String的長度用.length()int[] cntP = new int[26]; //統計p的每種字母的出現次數int[] cntS = new int[26]; //統計s的長為p.length()的子串s'的每種字母的出現次數for(char c:p.toCharArray()){cntP[c - 'a']++;}for(int right = 0;right < n;right++){cntS[s.charAt(right) - 'a']++;int left = right - p.length() + 1;if(left < 0){continue; //窗口長度不夠}if(Arrays.equals(cntS,cntP)){ans.add(left);}cntS[s.charAt(left) - 'a']--; //左端字母離開窗口}return ans;}
}

Arrays.equals(cntS, cntP) 是 Java 中用來 判斷兩個數組是否“完全相同” 的標準方法

? 它比較的是：

兩個數組在以下方面是否完全一致：

比較項	是否比較
1. 數組長度	是
2. 每個對應位置的元素值	是
3. 元素順序	是（順序不同 → 不相等）

如果以上全部相同，返回 true；否則返回 false。

---

定長滑窗套路

窗口右端點在 i 時，由于窗口長度為 k，所以窗口左端點為 i?k+1。

三步：入-更新-出

1. 入：下標為 i 的元素進入窗口，更新相關統計量。如果窗口左端點 i?k+1<0，則尚未形成第一個窗口，重復第一步。
2. 更新：更新答案。一般是更新最大值/最小值。
3. 出：下標為 i?k+1 的元素離開窗口，更新相關統計量，為下一個循環做準備。

不定長滑窗

class Solution {public List<Integer> findAnagrams(String s, String p) {List<Integer> ans = new ArrayList<>();int[] cnt = new int[26]; // 統計 p 的每種字母的出現次數for (char c : p.toCharArray()) {cnt[c - 'a']++; //s中出現就-- 若cnt<0則說明子串c太多 }int left = 0;for (int right = 0; right < s.length(); right++) {int c = s.charAt(right) - 'a';cnt[c]--; // 右端點字母進入窗口while (cnt[c] < 0) { // 字母 c 太多了cnt[s.charAt(left) - 'a']++; // 左端點字母離開窗口left++;}if (right - left + 1 == p.length()) { // s' 和 p 的每種字母的出現次數都相同ans.add(left); // s' 左端點下標加入答案}}return ans;}
}

代碼實現時，可以把 cntS 和 cntP 合并成一個 cnt：

• 對于 p 的字母 c，把 cnt[p] ++

• 對于 s’ 的字母 c，把 cnt[c] –

• 如果 cnt[c]<0，說明窗口中的字母 c 的個數比 p 的多，右移左端點。

D3

560. 和為 K 的子數組

560. 和為 K 的子數組

暴力

遍歷得到所有子串并求和 篩選出符合條件的

class Solution {public int subarraySum(int[] nums, int k) {int ans = 0;int n = nums.length;for(int i = 0;i < n;i++){  //列舉每個元素當子串結尾的情況int sum = 0;for(int j = i;j >= 0;j--){  //求所有以這個子串為結尾的和sum += nums[j];if(sum == k)ans++;}}return ans;}
}

前綴和+哈希表

前綴和：pre[i]=pre[i?1]+nums[i]

[j…i] 這個子數組和為 k 這個條件我們可以轉化為pre[i]?pre[j?1]==k

簡單移項可得符合條件的下標 j 需要滿足

pre[j?1]==pre[i]?k

class Solution {public int subarraySum(int[] nums, int k) {int ans = 0,pre = 0;int n = nums.length;HashMap<Integer,Integer>mp = new HashMap<>();mp.put(0,1);for(int i = 0;i < n;i++){pre += nums[i];if(mp.containsKey(pre - k)){ans += mp.get(pre - k);}mp.put(pre,mp.getOrDefault(pre,0) + 1);}return ans;}
}

D4

239. 滑動窗口最大值

239. 滑動窗口最大值

單調隊列

單調隊列套路

1. 右邊入（元素進入隊尾，同時維護隊列單調性）
2. 左邊出（元素離開隊首）
3. 記錄/維護答案（根據隊首）

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;int[] ans = new int[n - k + 1]; // 窗口個數Deque<Integer> q = new ArrayDeque<>(); // 更快的寫法見【Java 數組】for (int i = 0; i < n; i++) {// 1. 右邊入while (!q.isEmpty() && nums[q.getLast()] <= nums[i]) {q.removeLast(); // 維護 q 的單調性}q.addLast(i); // 注意保存的是下標，這樣下面可以判斷隊首是否離開窗口// 2. 左邊出int left = i - k + 1; // 窗口左端點if (q.getFirst() < left) { // 隊首離開窗口q.removeFirst();}// 3. 在窗口左端點處記錄答案if (left >= 0) {// 由于隊首到隊尾單調遞減，所以窗口最大值就在隊首ans[left] = nums[q.getFirst()];}}return ans;}
}

D5

76. 最小覆蓋子串

76. 最小覆蓋子串

class Solution {public String minWindow(String S, String t) {int[] cntS = new int[128]; // s 子串字母的出現次數int[] cntT = new int[128]; // t 中字母的出現次數for (char c : t.toCharArray()) {cntT[c]++;}char[] s = S.toCharArray();int m = s.length;int ansLeft = -1;int ansRight = m;int left = 0;for (int right = 0; right < m; right++) { // 移動子串右端點cntS[s[right]]++; // 右端點字母移入子串 如果 s[right] 是一個 char 類型的字符，它會被自動轉換成對應的 ASCII/Unicode 數值（int），然后作為數組下標使用while (isCovered(cntS, cntT)) { // 涵蓋if (right - left < ansRight - ansLeft) { // 找到更短的子串ansLeft = left; // 記錄此時的左右端點ansRight = right;}cntS[s[left]]--; // 左端點字母移出子串left++;}}return ansLeft < 0 ? "" : S.substring(ansLeft, ansRight + 1);}private boolean isCovered(int[] cntS, int[] cntT) {for (int i = 'A'; i <= 'Z'; i++) {if (cntS[i] < cntT[i]) {return false;}}for (int i = 'a'; i <= 'z'; i++) {if (cntS[i] < cntT[i]) {return false;}}return true;}
}

D6

53. 最大子數組和

53. 最大子數組和

貪心

若指針所指當前元素之前的和小于0，則丟棄當前元素之前的數列

class Solution {public int maxSubArray(int[] nums) {int pre = 0, ans = nums[0];for (int x : nums) {if(pre < 0){pre = x;}else{pre += x;}ans = Math.max(pre,ans);}return ans;}
}

動態規劃

考慮 nums[i] 單獨成為一段還是加入 f(i?1) 對應的那一段，這取決于 nums[i] 和f(i?1)+nums[i] 的大小

class Solution {public int maxSubArray(int[] nums) {int pre = 0, maxAns = nums[0];for (int x : nums) {pre = Math.max(pre + x, x);maxAns = Math.max(maxAns, pre);}return maxAns;}
}

D7

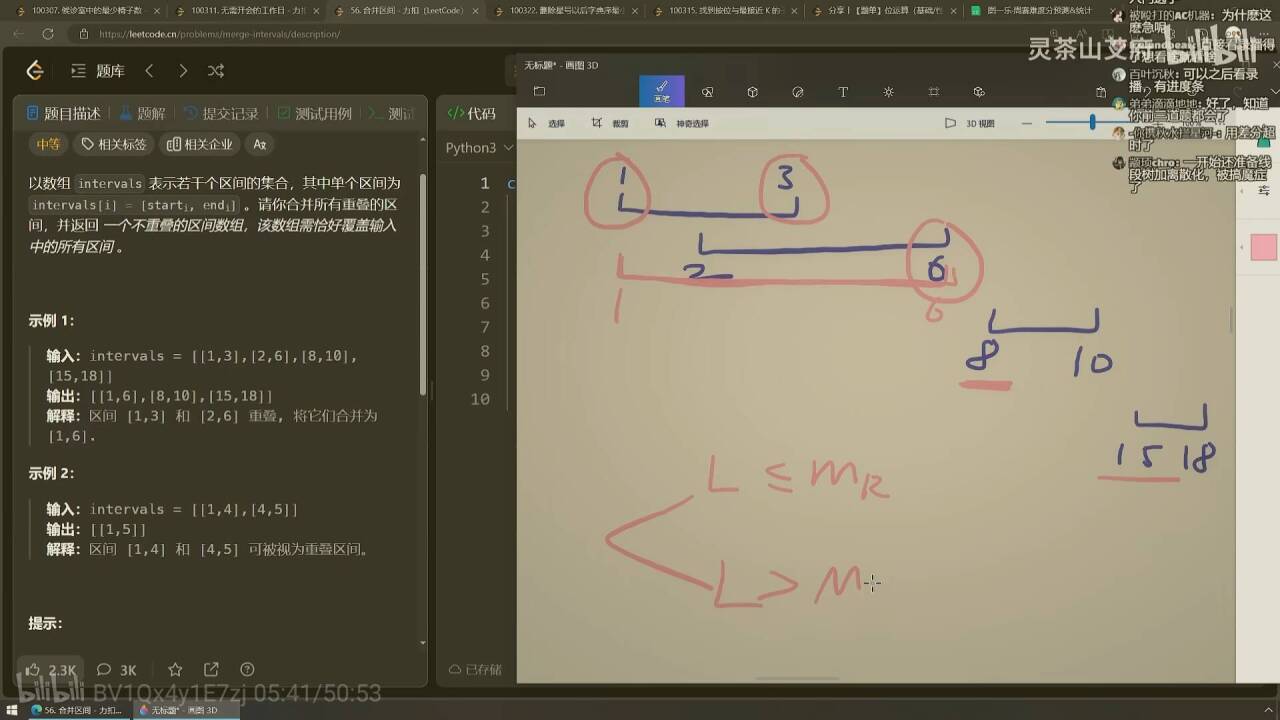
56. 合并區間

56. 合并區間

一開始想到三種區間關系，覆蓋，重疊，相離，不知道怎么把合并的區間添加到ans中

其實不用分出三種區間關系，直接判斷能否合并就行，即前一個的right和后一個left的關系：

• q_left <= p_right 可以合并
• q_left > p_right 不可以合并

對于最后將合并好的區間添加的ans里也可以簡單化：

• 可合并：添加前一個區間p進ans 修改p_right為q_right（如果q_right更大的話）
• 不可合并：直接將該區間加入
  

class Solution {public int[][] merge(int[][] intervals) {Arrays.sort(intervals, (p, q) -> p[0] - q[0]); // 按照左端點從小到大排序List<int[]> ans = new ArrayList<>(); //不知道最后結果大小 沒法用二維數組for (int[] p : intervals) {int m = ans.size();if (m > 0 && p[0] <= ans.get(m - 1)[1]) { // 可以合并ans.get(m - 1)[1] = Math.max(ans.get(m - 1)[1], p[1]); // 更新右端點最大值} else { // 不相交，無法合并ans.add(p);}}return ans.toArray(new int[ans.size()][]);}
}

return ans.toArray(new int[ans.size()][]);

作用是：將 List<int[]> 轉換為 int[][]（二維數組）并返回。

為什么要寫這一行？

• 函數的返回類型是 int[][]（二維數組）
• 但我們使用 List<int[]> 來動態存儲合并后的區間（因為 List 可以隨時 add，而數組大小固定）

所以，在最后必須把 List 轉成 int[][] 才能返回。