C數據結構：二叉樹

二叉樹的數據結構

前序遍歷

中序遍歷

后序遍歷

二叉樹的創建

二叉樹的銷毀

二叉樹的節點個數

二叉樹葉子節點個數

二叉樹第K層節點個數

二叉樹的查找

層序遍歷

判斷二叉樹是否為完全二叉樹

完整代碼

二叉樹的數據結構

typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;

這里二叉樹是使用了鏈式存儲

data負責存儲數據，left指針負責存儲左孩子節點，right負責存儲右孩子節點

前序遍歷

void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}

前序遍歷的規則是先訪問根節點，然后訪問左子樹，最后訪問右子樹

根據規則我們在遍歷前先打印當前根節點的值（若是遇到NULL則打印N代替空節點），然后再往下遞歸左子樹、右子樹即可?

中序遍歷

void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreeInOrder(root->_left);printf("%d ", root->_data);BinaryTreeInOrder(root->_right);
}

中序遍歷的規則是先訪問左子樹，然后訪問根節點，最后訪問右子樹

?所以這里先遞歸到左子樹（最左邊），然后打印當前節點的值，然后再訪問右子樹（右子樹的左子樹），打印值，循環往復

后序遍歷

void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%d ", root->_data);
}

?后序遍歷的規則是先訪問左子樹，然后訪問右子樹，最后訪問根節點

跟前面的前序遍歷和中序遍歷基本一致，都只是順序不一樣

二叉樹的創建

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->_data = a[(*pi)++];root->_left = BinaryTreeCreate(a, n, pi);root->_right = BinaryTreeCreate(a, n, pi);return root;
}

使用該函數需要傳一個數組，并根據數組里的元素當作前序遍歷構建起二叉樹

并需要傳一個數組的大小，和一個標記pi，在外面傳參的時候從數組開始的下標開始傳

這里為了讓函數在遞歸過程中能夠始終有一個變量能夠指向數組的某個元素來迭代（遍歷數組），不受遞歸變化而變化，所以需要一個指針變量，在下一次遞歸的時候只需要傳地址，就能獲得*pi的值，而不是通過傳參

?在每次遞歸過程中需要先創建一個根節點root并開辟一塊空間，并為該節點data賦值為當前走到的*pi的位置

接下來就要開始遞歸先從根的左子樹開始到右子樹，并分別賦值給root的左和右

這里的遞歸會一直遞歸，我們需要讓他遞歸到空為止，所以需要設定if語句限定遞歸次數

if語句限定了當*pi超過了數組的長度或等于數組長度時，則不能繼續遞歸獲取空間

所以這里是從最后一個節點開始往回返，先return最后一個節點給上一個遞歸的左或者右節點，依次往復即可

二叉樹的銷毀

void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;BinaryTreeDestory(root);BinaryTreeDestory(root);free(root);
}

銷毀我們需要用后序遍歷，因為前序和中序會先將根節點給銷毀了，這樣就不好往下找了，故此要使用后序遍歷來一個個free掉每一個節點

二叉樹的節點個數

int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeSize(root->_left)+ BinaryTreeSize(root->_right) + 1;
}

控制好遞歸的次數?

只需要在遍歷每一層節點時+1，即可

二叉樹葉子節點個數

int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->_left == NULL && root->_right == NULL)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

還是先控制遞歸的層數，當root等于空時往回返

若root的左和右都為空，則說明當前節點為葉子節點，返回1

最后返回左子樹葉子節點和右子樹葉子節點個數相加即可

二叉樹第K層節點個數

int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

?和前面的遞歸思路都差不多

這里返回1的條件是k == 1，因為只需要遞歸k-1次即可，當遞歸次數達到說明也到了第k層，則返回1即可

最后返回給外層的時候把左右子樹的結果返回起來相加即可

二叉樹的查找

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* ret1 = BinaryTreeFind(root->_left, x);if (ret1)return ret1;BTNode* ret2 = BinaryTreeFind(root->_right, x);if (ret2)return ret2;return NULL;
}

?第一個if語句控制層數

第二個判斷查找結果，若找到則返回根節點root

找到的結果返回給下面的ret1指針或者ret2指針，通過這兩個指針返回給最外層

層序遍歷

void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->_data);if (front->_left)QueuePush(&q, front->_left);if (front->_right)QueuePush(&q, front->_right);}QueueDestroy(&q);
}

層序遍歷是一層一層從左到右遍歷，那么我們就需要借助隊列來完成（先進先出）

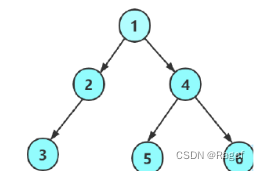
例如該圖層序遍歷后就是1，2，4，3，5，6

首先我們需要將根節點入隊列

然后進入循環，我們循環的條件是隊列為空則停止循環

所以我們還需要不斷入棧

這里第一層已經入棧了，這時候就可以拿到這個節點，我把它叫做front

后面我們就可以打印這個front節點的data

然后就可以刪除掉這個節點了，但是刪除的同時需要把它的左右孩子帶進來，但是左右孩子有可能為空，所以先判斷，若不為空則push入隊列，這樣第二層就入隊列了

接下來繼續pop2和4（pop的同時打印），然后push2和4的左右孩子

?最后不要忘記將隊列銷毀，防止造成內存泄漏

判斷二叉樹是否為完全二叉樹

int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q, front->_left);QueuePush(&q, front->_right);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){QueueDestroy(&q);return 0;}}QueueDestroy(&q);return 1;
}

和前面層序遍歷差不多，我們也需要借用一個隊列來完成該函數

先入第一個根節點進隊列，然后循環的將二叉樹的全部節點按照層序遍歷都push進去?

push到最后隊列的頭節點front總會碰到空節點，所以我們碰到空節點就break出去循環，這是第一個循環的主要作用

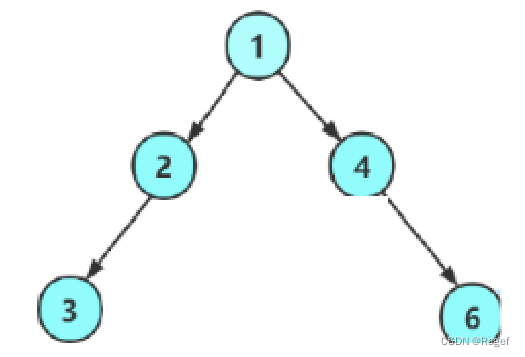
例如該二叉樹，我們push2的時候就會把左節點3和右節點NULL給入隊列，那么我們的front肯定會接收到NULL從而跳出循環

如上并不是一個完全二叉樹，所以我們判斷它不是完全二叉樹的理由就是根據層序遍歷它的空節點后面還有一個節點6

所以我們第二個循環的任務就是pop掉隊列剩下的所有值，若pop的時候發現里面還有非空節點，則不為完全二叉樹，return 0

例如我們在把NULL節點接收給front時，我們肯定會經過4這個節點，然后4這個節點就會把它的左NULL和右6兩個節點入隊列

所以我們最后在把隊列全部出掉的時候肯定會碰到這個6，既然碰到了這個6就說明這不是一個完全二叉樹

完整代碼

#include"BinaryTree.h"
#include"Queue.h"BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->_data = a[(*pi)++];root->_left = BinaryTreeCreate(a, n, pi);root->_right = BinaryTreeCreate(a, n, pi);return root;
}void BinaryTreeDestory(BTNode* root)
{if (root == NULL)return;BinaryTreeDestory(root);BinaryTreeDestory(root);free(root);
}int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeSize(root->_left)+ BinaryTreeSize(root->_right) + 1;
}int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->_left == NULL && root->_right == NULL)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* ret1 = BinaryTreeFind(root->_left, x);if (ret1)return ret1;BTNode* ret2 = BinaryTreeFind(root->_right, x);if (ret2)return ret2;return NULL;
}void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreeInOrder(root->_left);printf("%d ", root->_data);BinaryTreeInOrder(root->_right);
}void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%d ", root->_data);
}void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->_data);if (front->_left)QueuePush(&q, front->_left);if (front->_right)QueuePush(&q, front->_right);}QueueDestroy(&q);
}int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q, front->_left);QueuePush(&q, front->_right);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){QueueDestroy(&q);return 0;}}QueueDestroy(&q);return 1;
}

完