本文主要包含以下內容:
- 推導神經網絡的誤差反向傳播過程
- 使用numpy編寫簡單的神經網絡,并使用iris數據集和california_housing數據集分別進行分類和回歸任務,最終將訓練過程可視化。
1. BP算法的推導過程
1.1 導入
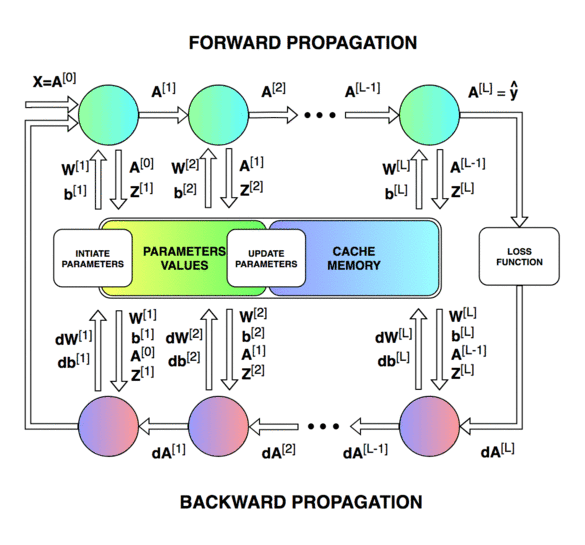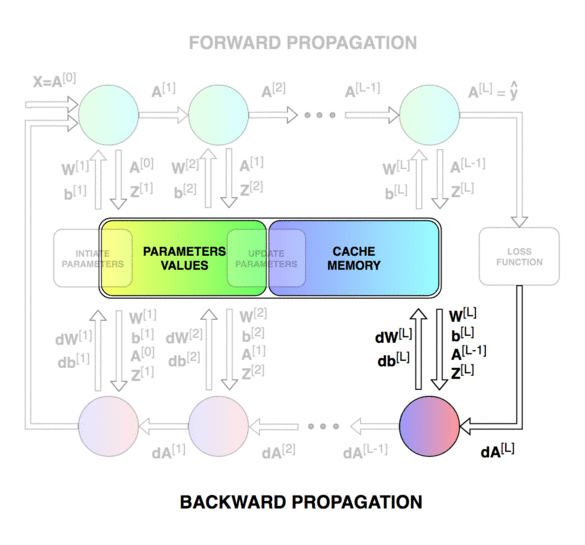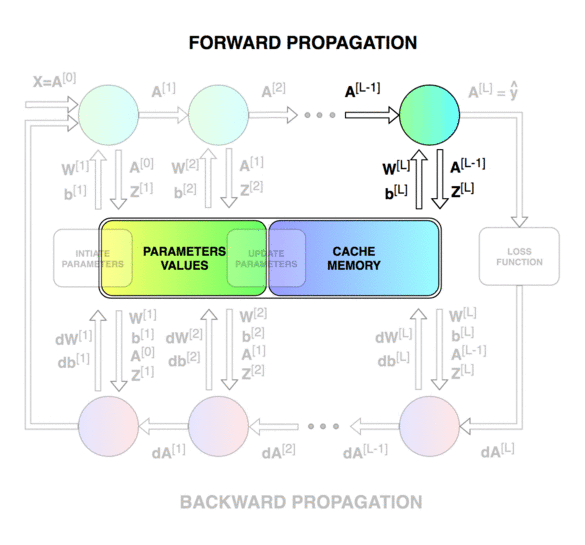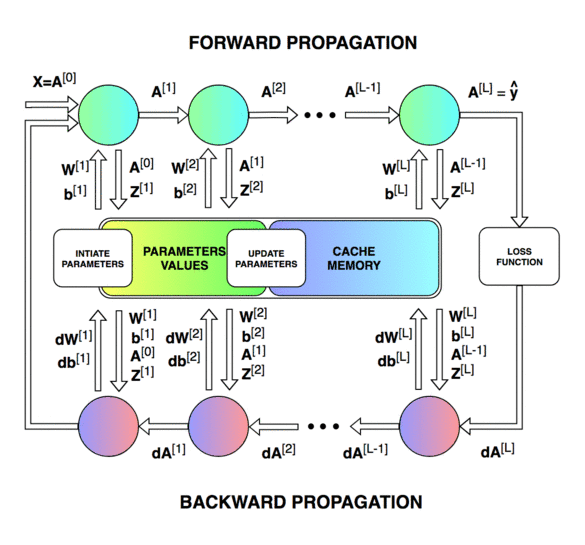
前向傳播和反向傳播的總體過程。
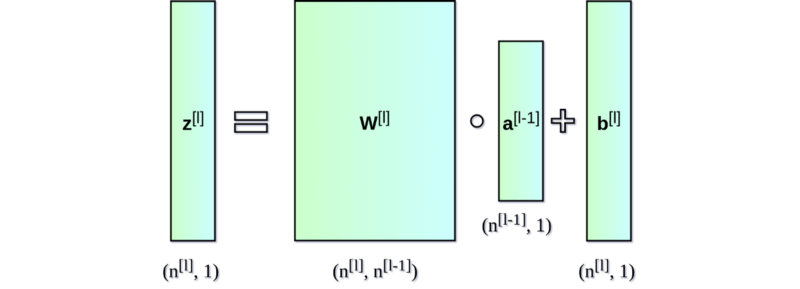
神經網絡的直接輸出記為 Z [ l ] Z^{[l]} Z[l],表示激活前的輸出,激活后的輸出記為 A A A。
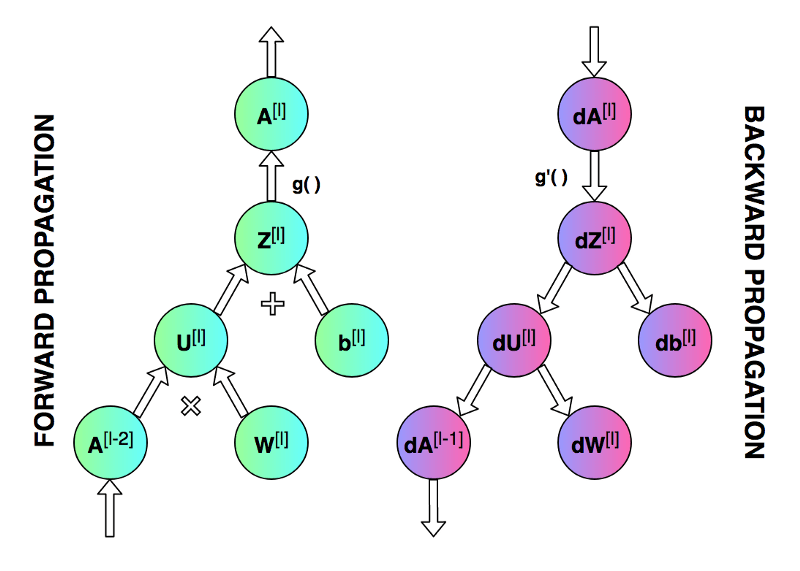
第一個圖像是神經網絡的前向傳遞和反向傳播的過程,第二個圖像用于解釋中間的變量關系,第三個圖像是前向和后向過程的計算圖,方便進行推導,但是第三個圖左下角的 A [ l ? 2 ] A^{[l-2]} A[l?2]有錯誤,應該是 A [ l ? 1 ] A^{[l-1]} A[l?1]。
1.2 符號表
為了方便進行推導,有必要對各個符號進行介紹
符號表
| 記號 | 含義 |
|---|---|
| n l n_l nl? | 第 l l l層神經元個數 |
| f l ( ? ) f_l(\cdot) fl?(?) | 第 l l l層神經元的激活函數 |
| W l ∈ R n l ? 1 × n l \mathbf{W}^l\in\R^{n_{l-1}\times n_{l}} Wl∈Rnl?1?×nl? | 第 l ? 1 l-1 l?1層到第 l l l層的權重矩陣 |
| b l ∈ R n l \mathbf{b}^l \in \R^{n_l} bl∈Rnl? | 第 l ? 1 l-1 l?1層到第 l l l層的偏置 |
| Z l ∈ R n l \mathbf{Z}^l \in \R^{n_l} Zl∈Rnl? | 第 l l l層的凈輸出,沒有經過激活的輸出 |
| A l ∈ R n l \mathbf{A}^l \in \R^{n_l} Al∈Rnl? | 第 l l l層經過激活函數的輸出, A 0 = X A^0=X A0=X |
深層的神經網絡都是由一個一個單層網絡堆疊起來的,于是我們可以寫出神經網絡最基本的結構,然后進行堆疊得到深層的神經網絡。
于是,我們可以開始編寫代碼,通過一個類Layer來描述單個神經網絡層
class Layer:def __init__(self, input_dim, output_dim):# 初始化參數self.W = np.random.randn(input_dim, output_dim) * 0.01self.b = np.zeros((1, output_dim))def forward(self, X):# 前向計算self.Z = np.dot(X, self.W) + self.bself.A = self.activation(self.Z)return self.Adef backward(self, dA, A_prev, activation_derivative):# 反向傳播# 計算公式推導見下方m = A_prev.shape[0]self.dZ = dA * activation_derivative(self.Z)self.dW = np.dot(A_prev.T, self.dZ) / mself.db = np.sum(self.dZ, axis=0, keepdims=True) / mdA_prev = np.dot(self.dZ, self.W.T)return dA_prevdef update_parameters(self, learning_rate):# 參數更新self.W -= learning_rate * self.dWself.b -= learning_rate * self.db# 帶有ReLU激活函數的Layer
class ReLULayer(Layer):def activation(self, Z):return np.maximum(0, Z)def activation_derivative(self, Z):return (Z > 0).astype(float)# 帶有Softmax激活函數(主要用于分類)的Layer
class SoftmaxLayer(Layer):def activation(self, Z):exp_z = np.exp(Z - np.max(Z, axis=1, keepdims=True))return exp_z / np.sum(exp_z, axis=1, keepdims=True)def activation_derivative(self, Z):# Softmax derivative is more complex, not directly used in this form.return np.ones_like(Z)
1.3 推導過程
權重更新的核心在于計算得到self.dW和self.db,同時,為了將梯度信息不斷回傳,需要backward函數返回梯度信息dA_prev。
需要用到的公式
Z l = W l A l ? 1 + b l A l = f ( Z l ) d Z d W = ( A l ? 1 ) T d Z d b = 1 Z^l = W^l A^{l-1} +b^l \\A^l = f(Z^l)\\\frac{dZ}{dW} = (A^{l-1})^T \\\frac{dZ}{db} = 1 Zl=WlAl?1+blAl=f(Zl)dWdZ?=(Al?1)TdbdZ?=1
解釋:
從上方計算圖右側的反向傳播過程可以看到,來自于上一層的梯度信息dA經過dZ之后直接傳遞到db,也經過dU之后傳遞到dW,于是我們可以得到dW和db的梯度計算公式如下:
d W = d A ? d A d Z ? d Z d W = d A ? f ′ ( d Z ) ? A p r e v T \begin{align}dW &= dA \cdot \frac{dA}{dZ} \cdot \frac{dZ}{dW}\\ &= dA \cdot f'(dZ) \cdot A_{prev}^T \\ \end{align} dW?=dA?dZdA??dWdZ?=dA?f′(dZ)?AprevT???
其中, f ( ? ) f(\cdot) f(?)是激活函數, f ′ ( ? ) f'(\cdot) f′(?)是激活函數的導數, A p r e v T A_{prev}^T AprevT?是當前層上一層激活輸出的轉置。
同理,可以得到
d b = d A ? d A d Z ? d Z d b = d A ? f ′ ( d Z ) \begin{align}db &= dA \cdot \frac{dA}{dZ} \cdot \frac{dZ}{db}\\ &= dA \cdot f'(dZ) \\ \end{align} db?=dA?dZdA??dbdZ?=dA?f′(dZ)??
需要僅需往前傳遞的梯度信息:
d A p r e v = d A ? d A d Z ? d Z A p r e v = d A ? f ′ ( d Z ) ? W T \begin{align}dA_{prev} &= dA \cdot \frac{dA}{dZ} \cdot \frac{dZ}{A_{prev}}\\ &= dA \cdot f'(dZ) \cdot W^T \\ \end{align} dAprev??=dA?dZdA??Aprev?dZ?=dA?f′(dZ)?WT??
所以,經過上述推導,我們可以將梯度信息從后向前傳遞。
分類損失函數
分類過程的損失函數最常見的就是交叉熵損失了,用來計算模型輸出分布和真實值之間的差異,其公式如下:
L = ? 1 N ∑ i = 1 N ∑ j = 1 C y i j l o g ( y i j ^ ) L = -\frac{1}{N}\sum_{i=1}^N \sum_{j=1}^C{y_{ij} log(\hat{y_{ij}})} L=?N1?i=1∑N?j=1∑C?yij?log(yij?^?)
其中, N N N表示樣本個數, C C C表示類別個數, y i j y_{ij} yij?表示第i個樣本的第j個位置的值,由于使用了獨熱編碼,因此每一行僅有1個數字是1,其余全部是0,所以,交叉熵損失每次需要對第 i i i個樣本不為0的位置的概率計算對數,然后將所有所有概率取平均值的負數。
交叉熵損失函數的梯度可以簡潔地使用如下符號表示:
? z L = y ^ ? y \nabla_zL = \mathbf{\hat{y}} - \mathbf{{y}} ?z?L=y^??y
回歸損失函數
均方差損失函數由于良好的性能被回歸問題廣泛采用,其公式如下:
L = 1 N ∑ i = 1 N ( y i ? y i ^ ) 2 L = \frac{1}{N} \sum_{i=1}^N(y_i - \hat{y_i})^2 L=N1?i=1∑N?(yi??yi?^?)2
向量形式:
L = 1 N ∣ ∣ y ? y ^ ∣ ∣ 2 2 L = \frac{1}{N} ||\mathbf{y} - \mathbf{\hat{y}}||^2_2 L=N1?∣∣y?y^?∣∣22?
梯度計算:
? y ^ L = 2 N ( y ^ ? y ) \nabla_{\hat{y}}L = \frac{2}{N}(\mathbf{\hat{y}} - \mathbf{y}) ?y^??L=N2?(y^??y)
2 代碼
2.1 分類代碼
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import matplotlib.pyplot as pltclass Layer:def __init__(self, input_dim, output_dim):self.W = np.random.randn(input_dim, output_dim) * 0.01self.b = np.zeros((1, output_dim))def forward(self, X):self.Z = np.dot(X, self.W) + self.b # 激活前的輸出self.A = self.activation(self.Z) # 激活后的輸出return self.Adef backward(self, dA, A_prev, activation_derivative):# 注意:梯度信息是反向傳遞的: l+1 --> l --> l-1# A_prev是第l-1層的輸出,也即A^{l-1}# dA是第l+1的層反向傳遞的梯度信息# activation_derivative是激活函數的導數# dA_prev是傳遞給第l-1層的梯度信息m = A_prev.shape[0]self.dZ = dA * activation_derivative(self.Z)self.dW = np.dot(A_prev.T, self.dZ) / mself.db = np.sum(self.dZ, axis=0, keepdims=True) / mdA_prev = np.dot(self.dZ, self.W.T) # 反向傳遞給下一層的梯度信息return dA_prevdef update_parameters(self, learning_rate):self.W -= learning_rate * self.dWself.b -= learning_rate * self.dbclass ReLULayer(Layer):def activation(self, Z):return np.maximum(0, Z)def activation_derivative(self, Z):return (Z > 0).astype(float)class SoftmaxLayer(Layer):def activation(self, Z):exp_z = np.exp(Z - np.max(Z, axis=1, keepdims=True))return exp_z / np.sum(exp_z, axis=1, keepdims=True)def activation_derivative(self, Z):# Softmax derivative is more complex, not directly used in this form.return np.ones_like(Z)class NeuralNetwork:def __init__(self, layer_dims, learning_rate=0.01):self.layers = []self.learning_rate = learning_ratefor i in range(len(layer_dims) - 2):self.layers.append(ReLULayer(layer_dims[i], layer_dims[i + 1]))self.layers.append(SoftmaxLayer(layer_dims[-2], layer_dims[-1]))def cross_entropy_loss(self, y_true, y_pred):n_samples = y_true.shape[0]y_pred_clipped = np.clip(y_pred, 1e-12, 1 - 1e-12)return -np.sum(y_true * np.log(y_pred_clipped)) / n_samplesdef accuracy(self, y_true, y_pred):y_true_labels = np.argmax(y_true, axis=1)y_pred_labels = np.argmax(y_pred, axis=1)return np.mean(y_true_labels == y_pred_labels)def train(self, X, y, epochs):loss_history = []for epoch in range(epochs):A = X# Forward propagationcache = [A]for layer in self.layers:A = layer.forward(A)cache.append(A)loss = self.cross_entropy_loss(y, A)loss_history.append(loss)# Backward propagation# 損失函數求導dA = A - yfor i in reversed(range(len(self.layers))):layer = self.layers[i]A_prev = cache[i]dA = layer.backward(dA, A_prev, layer.activation_derivative)# Update parametersfor layer in self.layers:layer.update_parameters(self.learning_rate)if (epoch + 1) % 100 == 0:print(f'Epoch {epoch + 1}/{epochs}, Loss: {loss:.4f}')return loss_historydef predict(self, X):A = Xfor layer in self.layers:A = layer.forward(A)return A# 導入數據
iris = load_iris()
X = iris.data
y = iris.target.reshape(-1, 1)# One hot encoding
encoder = OneHotEncoder(sparse_output=False)
y = encoder.fit_transform(y)# 分割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 定義并訓練神經網絡
layer_dims = [X_train.shape[1], 100, 20, y_train.shape[1]] # Example with 2 hidden layers
learning_rate = 0.01
epochs = 5000nn = NeuralNetwork(layer_dims, learning_rate)
loss_history = nn.train(X_train, y_train, epochs)# 預測和評估
train_predictions = nn.predict(X_train)
test_predictions = nn.predict(X_test)train_acc = nn.accuracy(y_train, train_predictions)
test_acc = nn.accuracy(y_test, test_predictions)print(f'Training Accuracy: {train_acc:.4f}')
print(f'Test Accuracy: {test_acc:.4f}')# 繪制損失曲線
plt.plot(loss_history)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Loss Curve')
plt.show()輸出
Epoch 100/1000, Loss: 1.0983
Epoch 200/1000, Loss: 1.0980
Epoch 300/1000, Loss: 1.0975
Epoch 400/1000, Loss: 1.0960
Epoch 500/1000, Loss: 1.0891
Epoch 600/1000, Loss: 1.0119
Epoch 700/1000, Loss: 0.6284
Epoch 800/1000, Loss: 0.3711
Epoch 900/1000, Loss: 0.2117
Epoch 1000/1000, Loss: 0.1290
Training Accuracy: 0.9833
Test Accuracy: 1.0000
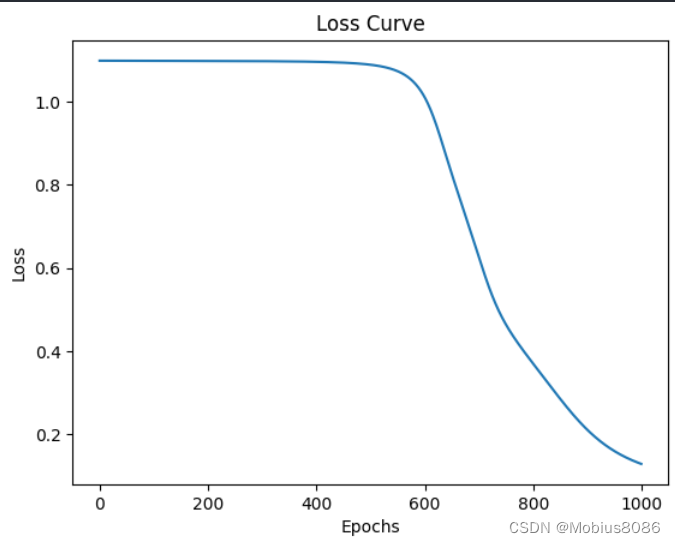
可以看到經過1000輪迭代,最終的準確率到達100%。
回歸代碼
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housingclass Layer:def __init__(self, input_dim, output_dim):self.W = np.random.randn(input_dim, output_dim) * 0.01self.b = np.zeros((1, output_dim))def forward(self, X):self.Z = np.dot(X, self.W) + self.bself.A = self.activation(self.Z)return self.Adef backward(self, dA, X, activation_derivative):m = X.shape[0]self.dZ = dA * activation_derivative(self.Z)self.dW = np.dot(X.T, self.dZ) / mself.db = np.sum(self.dZ, axis=0, keepdims=True) / mdA_prev = np.dot(self.dZ, self.W.T)return dA_prevdef update_parameters(self, learning_rate):self.W -= learning_rate * self.dWself.b -= learning_rate * self.dbclass ReLULayer(Layer):def activation(self, Z):return np.maximum(0, Z)def activation_derivative(self, Z):return (Z > 0).astype(float)class LinearLayer(Layer):def activation(self, Z):return Zdef activation_derivative(self, Z):return np.ones_like(Z)class NeuralNetwork:def __init__(self, layer_dims, learning_rate=0.01):self.layers = []self.learning_rate = learning_ratefor i in range(len(layer_dims) - 2):self.layers.append(ReLULayer(layer_dims[i], layer_dims[i + 1]))self.layers.append(LinearLayer(layer_dims[-2], layer_dims[-1]))def mean_squared_error(self, y_true, y_pred):return np.mean((y_true - y_pred) ** 2)def train(self, X, y, epochs):loss_history = []for epoch in range(epochs):A = X# Forward propagationcache = [A]for layer in self.layers:A = layer.forward(A)cache.append(A)loss = self.mean_squared_error(y, A)loss_history.append(loss)# Backward propagation# 損失函數求導dA = -(y - A)for i in reversed(range(len(self.layers))):layer = self.layers[i]A_prev = cache[i]dA = layer.backward(dA, A_prev, layer.activation_derivative)# Update parametersfor layer in self.layers:layer.update_parameters(self.learning_rate)if (epoch + 1) % 100 == 0:print(f'Epoch {epoch + 1}/{epochs}, Loss: {loss:.4f}')return loss_historydef predict(self, X):A = Xfor layer in self.layers:A = layer.forward(A)return Ahousing = fetch_california_housing()# 導入數據
X = housing.data
y = housing.target.reshape(-1, 1)# 標準化
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X = scaler_X.fit_transform(X)
y = scaler_y.fit_transform(y)# 分割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 定義并訓練神經網絡
layer_dims = [X_train.shape[1], 50, 5, 1] # Example with 2 hidden layers
learning_rate = 0.8
epochs = 1000nn = NeuralNetwork(layer_dims, learning_rate)
loss_history = nn.train(X_train, y_train, epochs)# 預測和評估
train_predictions = nn.predict(X_train)
test_predictions = nn.predict(X_test)train_mse = nn.mean_squared_error(y_train, train_predictions)
test_mse = nn.mean_squared_error(y_test, test_predictions)print(f'Training MSE: {train_mse:.4f}')
print(f'Test MSE: {test_mse:.4f}')# 繪制損失曲線
plt.plot(loss_history)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Loss Curve')
plt.show()輸出
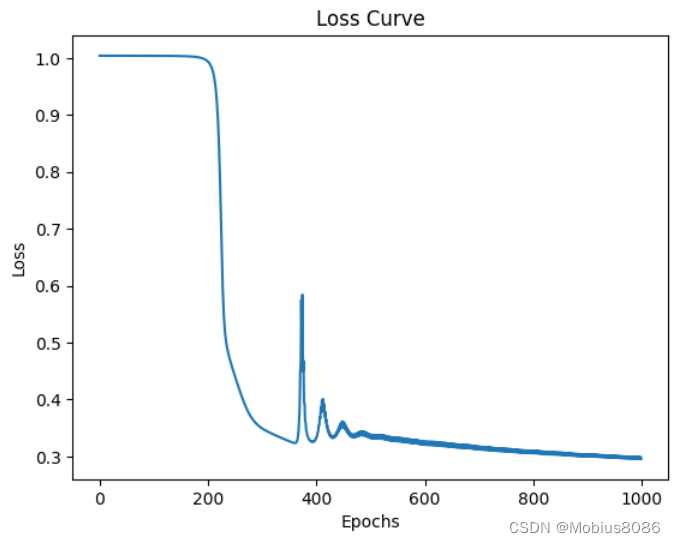
Epoch 100/1000, Loss: 1.0038
Epoch 200/1000, Loss: 0.9943
Epoch 300/1000, Loss: 0.3497
Epoch 400/1000, Loss: 0.3306
Epoch 500/1000, Loss: 0.3326
Epoch 600/1000, Loss: 0.3206
Epoch 700/1000, Loss: 0.3125
Epoch 800/1000, Loss: 0.3057
Epoch 900/1000, Loss: 0.2999
Epoch 1000/1000, Loss: 0.2958
Training MSE: 0.2992
Test MSE: 0.3071











元素定位工具appium-inspector)







