目錄

一、引言：為什么我們需要分析算法效率？

二、算法效率的維度

2.1 時間復雜度（Time Complexity）

2.2 空間復雜度（Space Complexity）

三、深入理解算法時間復雜度

3.1 時間復雜度的基礎概念

3.2 大O表示法 (Big O Notation)

3.3 最好、最壞與平均情況

四、常見時間復雜度計算與示例

4.1 O(1) - 常數時間復雜度

4.2 O(N) - 線性時間復雜度

4.3 O(N2) - 平方時間復雜度

4.4?O(logN) - 對數時間復雜度

4.5?O(2?) - 指數時間復雜度

五、空間復雜度分析

5.1?O(1) - 常數空間復雜度

5.2?O(N) - 線性空間復雜度

5.3?遞歸調用的空間復雜度

六、常見復雜度對比與可視化

七、總結

---

一、引言：為什么我們需要分析算法效率？

? ? ? ? 在編程的世界中，我們常常需要用多種算法來解決同一個問題。例如，計算斐波那契數列可以使用遞歸方法

public static long Fib(int N) {if (N <= 2) return 1;return Fib(N - 1) + Fib(N - 2);
}

????????這段代碼雖然簡潔，但是效率極低。當N的值較大時，程序運行時間程指數級增長，甚至可能導致棧溢出。

? ? ? ? 為了科學衡量算法的優劣，我們引入了時間復雜度和空間復雜度的概念。

二、算法效率的維度

2.1 時間復雜度（Time Complexity）

衡量算法執行所需的時間，通常表示為輸入規模的函數。我們關注的是隨著輸入規模的增大，算法執行時間的增長趨勢，而非具體的執行時間。

2.2 空間復雜度（Space Complexity）

衡量算法執行過程中所需的額外內存空間。同樣表示為輸入規模的函數，關注內存使用量的增長趨勢。

隨著硬件技術的發展，存儲空間成本大幅降低，時間復雜度往往成為我們更關注的指標。但在嵌入式系統或大數據處理場景中，空間復雜度仍然至關重要。

三、深入理解算法時間復雜度

3.1 時間復雜度的基礎概念

算法的時間復雜度不是測量具體的執行時間，而是計算基本操作的執行次數。這是因為：

• 不同的硬件環境執行時間不同
• 不同的編程語言執行效率不同
• 不同的編譯器優化程度不同

通過計算基本操作次數，我們可以得到與環境無關的算法效率衡量標準。

3.2 大O表示法 (Big O Notation)

大O表示法描述了算法的漸進行為，提供了復雜度分析的上界。推導方法為：

1. 用常數1取代運行時間中的所有加法常數
2. 在修改后的運行次數函數中，只保留最高階項
3. 如果最高階項存在且不是1，則去除與這個項相乘的常數

實際案例分析：

void func1(int N) {int count = 0;//第一個嵌套循環：N x N 次for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {count++:}}//第二個循環：2 x N 次for (int k = 0; k < 2*N; k++) {count++;}//第三個循環：10次int M = 10;while (M > 0) {count++;M--;}
}

該函數的總執行次數為：F(N) = N2 + 2N + 10

使用大O表示法：

• 去除常數項：N2 + 2N
• 只保留最高階項：N2
• 去除系數：N2

因此，時間復雜度為 O(N2)

3.3 最好、最壞與平均情況

算法性能可能因輸入數據的不同而變化：

• 最好情況：最小運行次數（下界）
• 最壞情況：最大運行次數（上界，通常我們關注這個）
• 平均情況：期望運行次數
  ?

示例：數組中查找元素

int findElement(int[] array, int target) {for (int i = 0; i < array.length; i++) {if (array[i] == target) {return i;}}return -1;
}

• 最好情況：目標元素在第一個位置 → O(1)
• 最壞情況：目標元素在最后或不存在 → O(N)
• 平均情況：目標元素在中間某位置 → O(N/2) → 簡化為 O(N)
  ?

在實際分析中，我們通常關注最壞情況，因為這提供了算法性能的保證。

四、常見時間復雜度計算與示例

4.1 O(1) - 常數時間復雜度

void func1(int N) {int count = 0;for (int i = 0; i < 100; i++) {count++;}System.out.println(count);
}

無論輸入規模N多大，執行次數都是100次，因此是O(1)

4.2 O(N) - 線性時間復雜度

void func2(int N) {int count = 0;for (int i = 0; i < 2*N; i++) {count++;}int M = 10;while (M > 0) {count++;M--;}System.out.println(count);
}

執行次數是2N+10，簡化后是O(N)

4.3 O(N2) - 平方時間復雜度

void bubbleSort(int[] array) {for (int i = 0; i < array.length-1; i++) {boolean sorted = true;for (int j = 0; j < array.length-1-i; j++) {if (array[j] > array[i]) {int temp = array[j];array[j] = array[i];array[i] = temp;sorted = false;}}if (sorted == true) {break;}}
}

最壞情況下需要執行 (N-1) + (N-2) + ... + 1 = N(N-1)/2 次操作，簡化后為 O(N2)。

4.4?O(logN) - 對數時間復雜度

int binarySearch(int[] array, int val) {int left = 0;int right = array.length - 1;while (left <= right) {int mid = (left+right) / 2;if (array[mid] > val) {right = mid - 1;} else if (array[mid] < val) {left = mid + 1;} else {return mid;}}return -1;
}

二分查找每次將搜索范圍減半，因此時間復雜度是 O(logN)。

直觀理解對數復雜度：假設有一張紙，每次將其對折，問對折多少次后厚度會超過一定高度？這就是對數函數的增長模式。

4.5?O(2?) - 指數時間復雜度

int fibanacci(int N) {return N<2 ? N : fibanacci(N-1)+fibanacci(N-2);
}

遞歸計算斐波那契數列會形成一顆深度為N的二叉樹，節點數約為2?，因此時間復雜度為 O(2?)。

五、空間復雜度分析

空間復雜度衡量算法運行過程中臨時占用的存儲空間大小（不包括輸入數據本身占用的空間）。

5.1?O(1) - 常數空間復雜度

void bubbleSort(int[] array) {    //僅使用常數個額外變量：i、j和sortedfor (int i = 0; i < array.length-1; i++) {boolean sorted = true;for (int j = 0; j < array.length-1-i; j++) {if (array[j] > array[i]) {int temp = array[j];array[j] = array[i];array[i] = temp;sorted = false;}}if (sorted == true) {break;}}
}

只使用了end、sorted、i等常數個變量，空間復雜度為 O(1)。

5.2?O(N) - 線性空間復雜度

int[] fibonacci(int N) {int[] fibArray = new long int[N+1];fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= N; i++) {fibArray[i] = fibArray[i-1] + fibArray[i-2];}return fibArray;
}

創建了長度為n+1的數組，空間復雜度為 O(N)。

5.3?遞歸調用的空間復雜度

long factorial(int N) {return N<2 ? N : factorial(N-1)*N;
}

每次遞歸調用都會在調用棧上創建一個新的棧幀，遞歸深度為N，因此空間復雜度為 O(N)。

注意：遞歸算法的空間復雜度與遞歸深度相關，這可能成為限制算法實用性的因素。

六、常見復雜度對比與可視化

復雜度	增長趨勢
O(1)	恒定
O(logN)	緩慢增長
O(N)	線性增長
O(NlogN)	接近線性
O(N2)	快速增長
O(2?)	爆發式增長

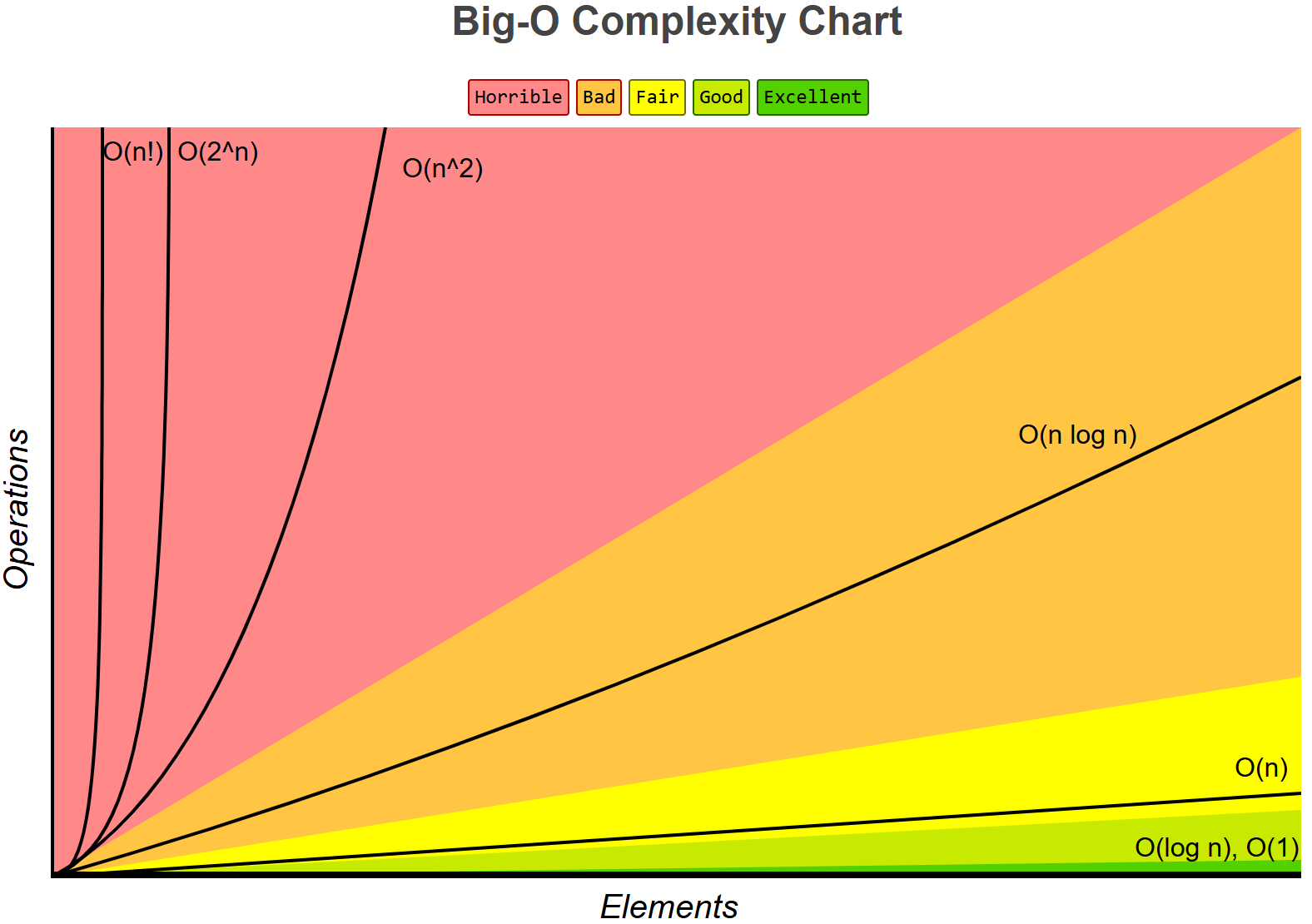
以下圖片可直觀體現各個復雜度的優劣：

七、總結

時間復雜度和空間復雜度是算法分析的核心概念，它們幫助我們：

1. 客觀評價算法效率，不受具體硬件環境影響
2. 預測算法在不同規模輸入下的性能表現
3. 在算法設計中做出合理的權衡決策
4. 為算法優化提供方向和目標

掌握復雜度分析不僅有助于編寫高效代碼，也是技術面試中必備的技能。通過理解各種常見算法的復雜度特征，我們能夠更好地選擇和應用合適的算法解決實際問題。

---

完