題目描述

給定一個 n × n 的二維矩陣 matrix 表示一個圖像。請你將圖像順時針旋轉 90 度。
你必須在 原地 旋轉圖像，這意味著你需要直接修改輸入的二維矩陣。請不要 使用另一個矩陣來旋轉圖像。

示例 1：

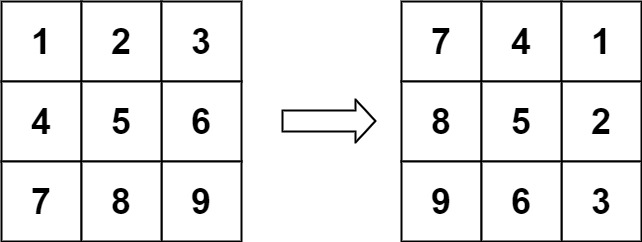
輸入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
輸出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：
輸入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
輸出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

思考一（轉置翻轉）

先轉置矩陣，再交換矩陣列

代碼

/*** @param {number[][]} matrix* @return {void} Do not return anything, modify matrix in-place instead.*/
var rotate = function(matrix) {const n = matrix.length;for (let i = 0; i < n; i++) {for (let j = 0; j < n; j++) {if (i <= j) {[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];}}}for (let i = 0; i < n; i++) {for (let j = 0; j < Math.floor(n/2); j++) {[matrix[i][j], matrix[i][n-j-1]] = [matrix[i][n-j-1], matrix[i][j]];}    }
};

思考二

分層旋轉（從外到內逐層處理），核心是通過 “臨時變量” 循環交換每一層的 4 個對應元素，同樣能實現原地旋轉。
將n×n矩陣看作“嵌套的正方形環”，從最外層（第0層）到最內層（第k層，k = Math.floor(n/2)），逐層處理每個環的元素：

• 對于第 layer 層（從0開始），該層的“邊長”為 len = n - 2*layer，需要處理 len-1 組元素（每組4個元素對應旋轉后的位置）。

• 每組元素的坐標規律（以第 layer 層為例）：

  • 左上角元素：(layer, layer + offset) → 旋轉后到右上角；
  • 右上角元素：(layer + offset, n-1 - layer) → 旋轉后到右下角；
  • 右下角元素：(n-1 - layer, n-1 - layer - offset) → 旋轉后到左下角；
  • 左下角元素：(n-1 - layer - offset, layer) → 旋轉后到左上角；
  • （offset 為每組的偏移量，從0到 len-2）。

• 時間復雜度$O(n^2)$

代碼

const n = matrix.length;// 從外到內逐層處理，共 Math.floor(n/2) 層for (let layer = 0; layer < Math.floor(n / 2); layer++) {const len = n - 2 * layer; // 當前層的邊長const last = n - 1 - layer; // 當前層的最后一個索引（行/列相同）// 處理當前層的每一組4個元素（共 len-1 組）for (let offset = 0; offset < len - 1; offset++) {// 1. 保存左上角元素（臨時變量）const temp = matrix[layer][layer + offset];// 2. 左下角 → 左上角matrix[layer][layer + offset] = matrix[last - offset][layer];// 3. 右下角 → 左下角matrix[last - offset][layer] = matrix[last][last - offset];// 4. 右上角 → 右下角matrix[last][last - offset] = matrix[layer + offset][last];// 5. 左上角（臨時）→ 右上角matrix[layer + offset][last] = temp;}}