算法 --- 分治（歸并）

分治（歸并）

分治（特別是歸并）算法適用于解決“整體求解依賴于子問題合并”且子問題相互獨立的題目，其典型特征是能將大規模數據分解、遞歸求解，然后通過合并操作（這正是歸并排序中‘歸并’的精髓）來構建最終答案。

什么樣的題目適用于分治（歸并）算法？

判斷一個題目是否適用分治（歸并）算法，主要看它是否滿足以下三個核心條件，尤其是第三個“合并”步驟：

可分解性：問題能夠被遞歸地分解成若干個規模更小、結構相同的子問題。
- 例子：?對一個數組排序，可以分解為對左半部分和右半部分分別排序。
子問題獨立性：分解出的子問題之間是相互獨立的，解決其中一個不會影響另一個。
- 這是分治與動態規劃（DP）的關鍵區別。DP的子問題是重疊的，需要記憶化。
可合并性（最關鍵）：問題的解能夠通過合并所有子問題的解來高效地得到。
- 這是“歸并”思想的體現。?合并過程往往不是簡單的相加，而是需要一個精心設計的算法步驟。

常見的題目類型（不僅僅是排序）

基于以上特點，分治（歸并）算法主要適用于以下幾類題目：

1. 分治排序與選擇

這是最經典的應用，直接體現了“分治”和“歸并”的思想。

歸并排序：將數組分成兩半，分別排序后，再合并兩個有序數組。
快速排序：也是一種分治，但核心是“劃分”而非“歸并”。
求逆序對：在歸并排序的合并過程中，可以高效地統計出跨越左右兩個子數組的逆序對數量，這是分治法的典范應用。

2. 大規模計算與統計問題

當問題需要處理大規模數據（如數組、矩陣）并計算某種聚合關系時，分治非常有效。

計算右側小于當前元素的個數：與求逆序對思路類似，在歸并排序的同時記錄答案。
區間和的統計問題：例如，給定數組，求有多少個連續子數組的和在某個范圍內。可以通過“歸并排序求前綴和數組”的方式來解決。

3. 高級數據結構相關

許多高效的數據結構其底層操作就是分治。

線段樹：構建、查詢、更新操作都是典型的分治（一分為二）。
字典樹、堆等結構的某些操作也蘊含分治思想。

4. 樹與圖的相關問題

樹結構本身就是一個遞歸（分治）結構。

樹的遍歷：前序、中序、后序遍歷本身就是“先處理左子樹（子問題1），再處理右子樹（子問題2），最后處理根（合并）”的分治過程。
最近公共祖先等問題常用分治思想解決。

5. 數學計算問題

一些經典算法本身就是分治。

大整數乘法（Karatsuba算法）：將大數分成小塊進行計算后再合并。
快速傅里葉變換：通過分治將多項式系數表示法轉換為點值表示法，極大加速了卷積運算。

總結：一個簡單的判斷方法

當你看到一個題目時，可以問自己：
“如果我把輸入數據分成兩半，分別求出兩半的答案，我能否有效地通過這兩個答案推導出整個問題的答案？”

如果答案是肯定的，并且子問題可以繼續這樣分解下去，那么這個問題就非常適合用分治（歸并）算法來解決。其中，“有效地推導”這個過程就是“歸并”操作的核心。

題目練習

912. 排序數組 - 力扣（LeetCode）

解法（歸并排序）：

算法思路：

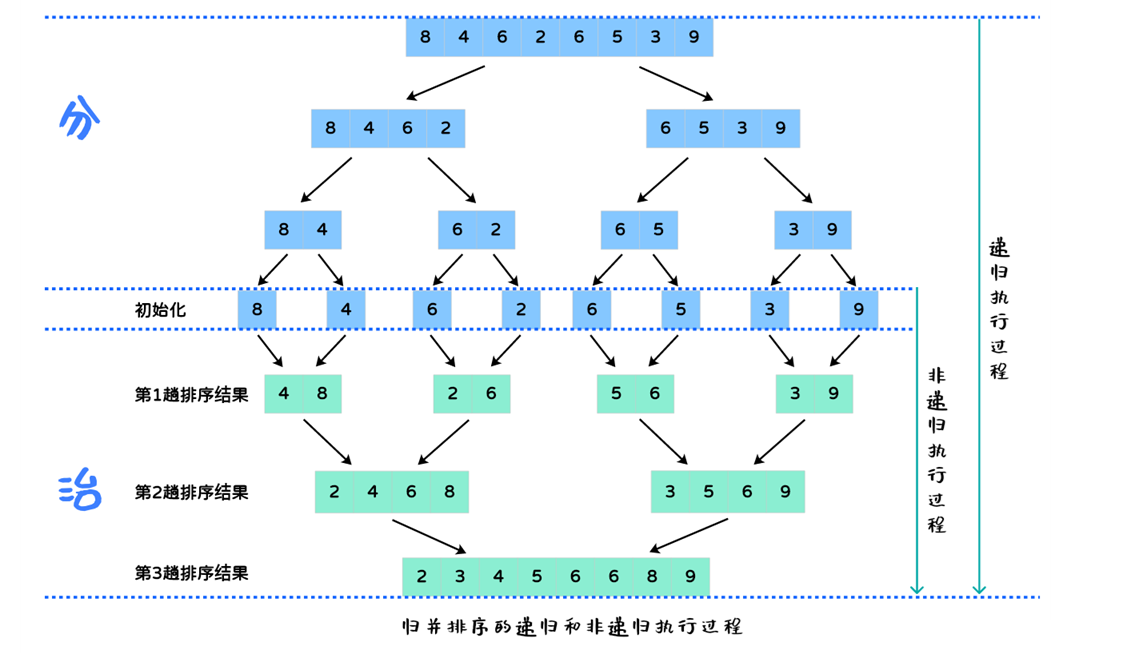
歸并排序的流程充分的體現了「分而治之」的思想，大體過程分為兩步：

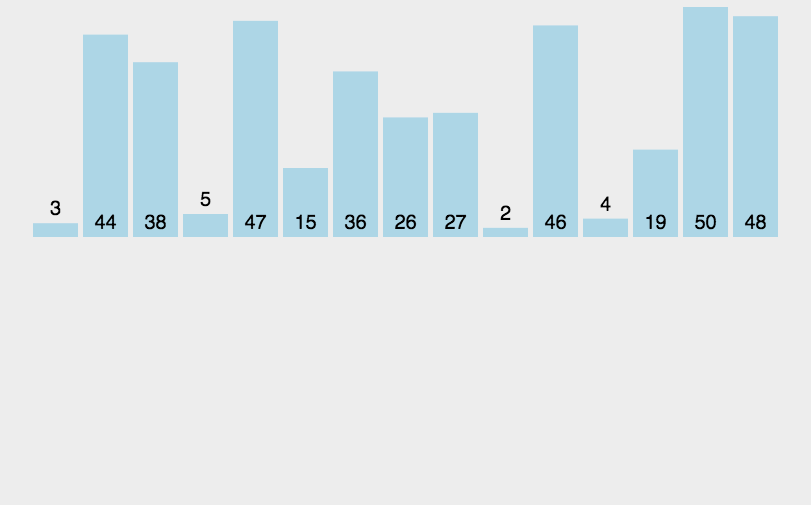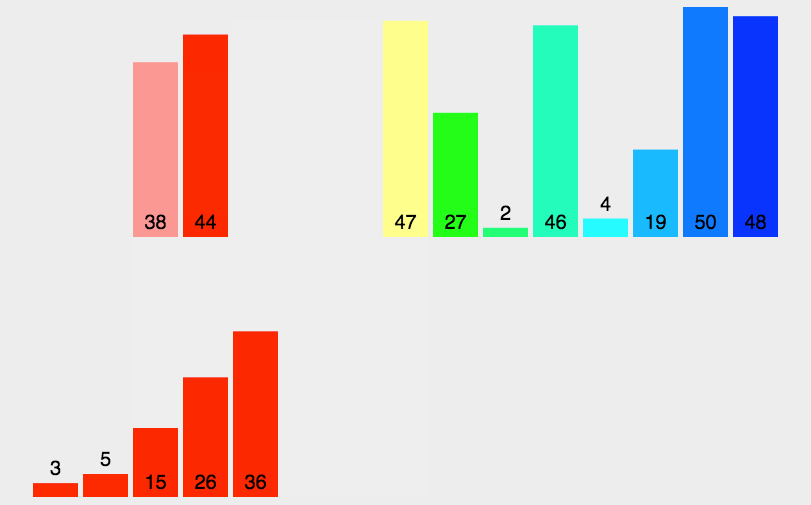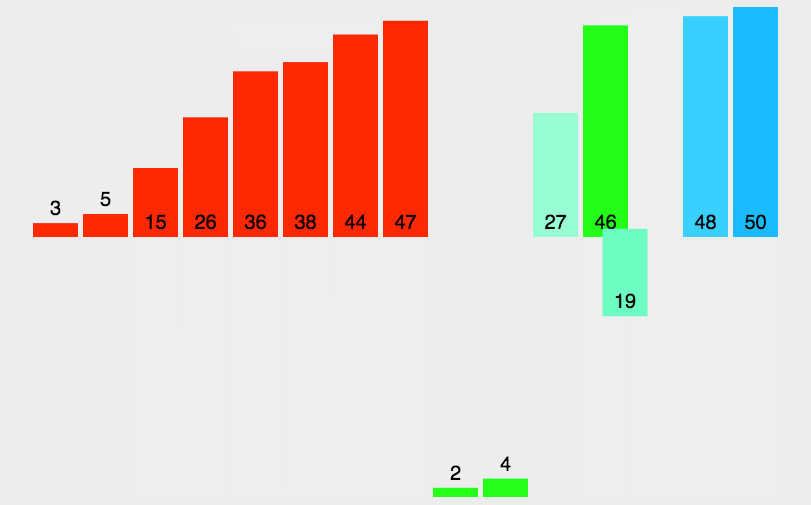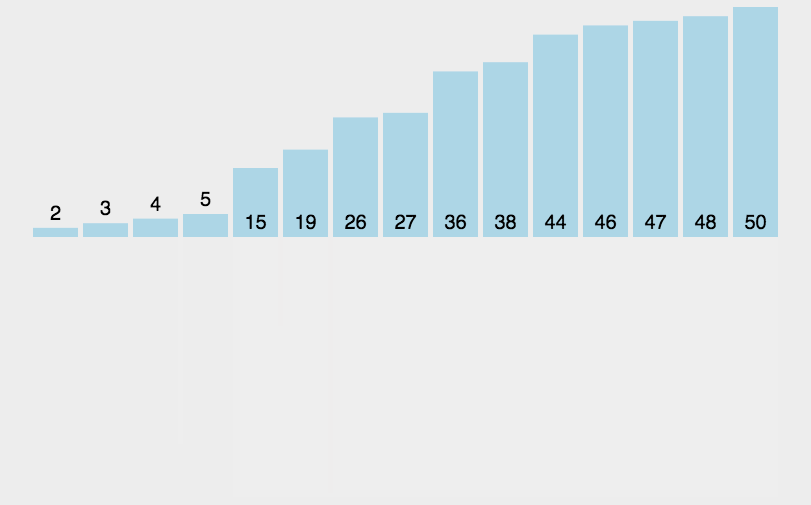
分：將數組一分為二為兩部分，一直分解到數組的長度為 1，使整個數組的排序過程被分為「左半部分排序」+「右半部分排序」；
治：將兩個較短的「有序數組」合并成一個長的有序數組，一直合并到最初的長度。

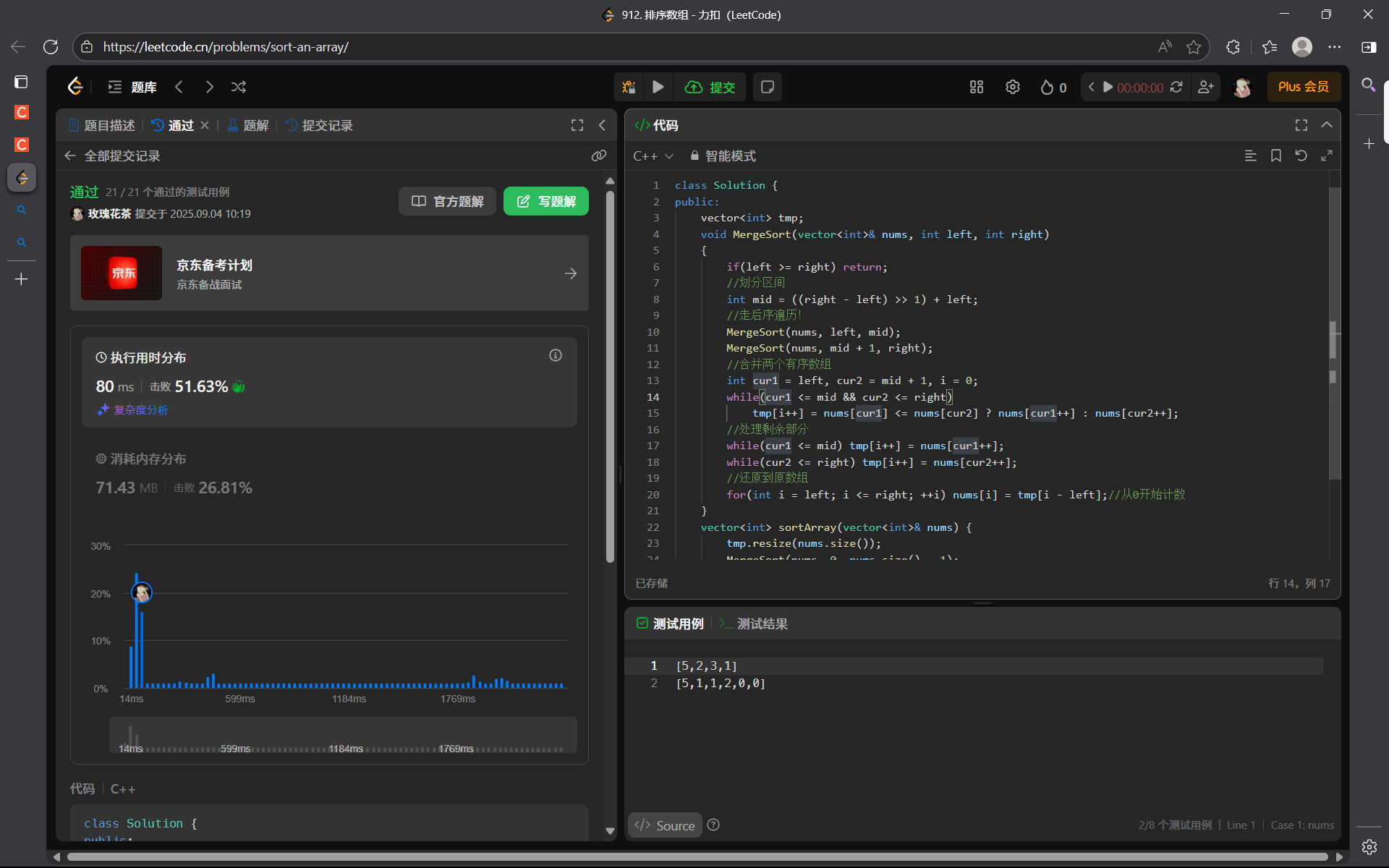
class Solution {
public:vector<int> tmp;void MergeSort(vector<int>& nums, int left, int right){if(left >= right) return;//劃分區間int mid = ((right - left) >> 1) + left;//走后序遍歷！MergeSort(nums, left, mid);MergeSort(nums, mid + 1, right);//合并兩個有序數組int cur1 = left, cur2 = mid + 1, i = 0;while(cur1 <= mid && cur2 <= right)tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];//處理剩余部分while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];//還原到原數組for(int i = left; i <= right; ++i) nums[i] = tmp[i - left];//從0開始計數}vector<int> sortArray(vector<int>& nums) {tmp.resize(nums.size());MergeSort(nums, 0, nums.size() - 1);return nums;}
};

LCR 170. 交易逆序對的總數 - 力扣（LeetCode）

歸并排序與逆序對統計

算法思路

在歸并排序中統計逆序對的數量是非常經典的應用。主要就是在歸并排序的合并過程中統計逆序對的數量，也就是合并兩個有序序列的過程中，快速找出逆序對的數量。

我們將這個問題分解成幾個小問題，逐一破解：

默認都是升序：如果掌握升序的話，降序的歸并過程也是可以解決的。
先解決第一個問題：為什么可以利用歸并排序？
- 逆序對中兩個元素：全部從左數組中選擇
- 逆序對中兩個元素：全部從右數組中選擇
- 逆序對中兩個元素：一個選左數組另一個選右數組

根據排列組合的分類相加原理，三種情況下產生的逆序對的總和，正好等于總的逆序對數量。

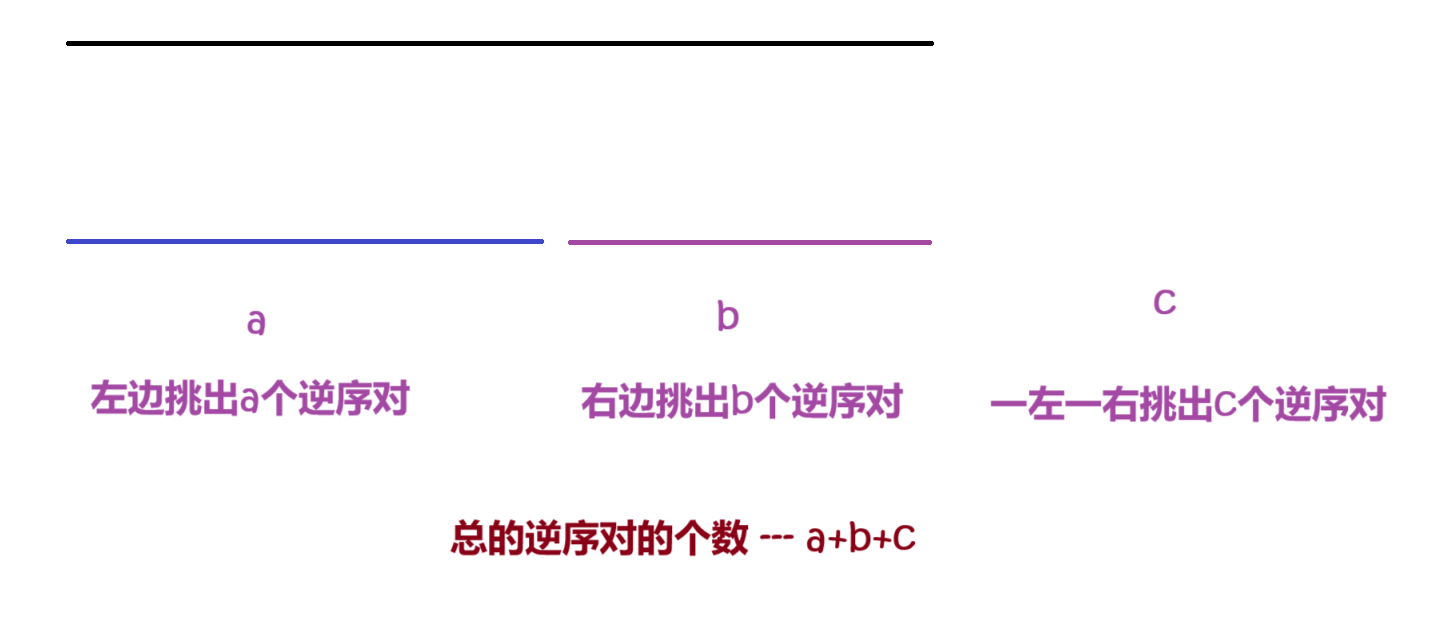
我們然后也在一左一右也在后面加排序！

歸并排序的過程

歸并排序的過程分為兩步：

分：將數組一分為二，一直分解到數組的長度為1，使整個數組的排序過程被分為「左半部分排序」+「右半部分排序」；
治：將兩個較短的有序數組合并成一個長的有序數組，一直合并到最初的長度。

解決第二個問題

在歸并排序合并的過程中，我們得到的是兩個有序的數組。我們可以利用數組的有序性，快速統計出逆序對的數量，而不是將所有情況都枚舉出來。

方法一：快速統計出某個數前面有多少個數比它大

通過一個示例來演示方法二：

假定已經有兩個已經有序的序列以及輔助數組 left=[5,7,9] right=[4,5,8] help=[]，通過合并兩個有序數組的過程，來求得逆序對的數量。

示例過程

第一輪循環：
- left[cur1] > right[cur2]，將 right[cur2] 加入到輔助數組中去，cur2++ 遍歷下一個元素。
- ret = 3，cur1 = 3 cur2 = 1
第二輪循環：
- left[cur1] == right[cur2]，將 left[cur1] 放入到輔助數組中去，cur1++ 遍歷下一個元素。
- ret = 3 cur1 = 4 cur2 = 1
第三輪循環：
- left[cur1] > right[cur2]，將 right[cur2] 加入到輔助數組中去，cur2++ 遍歷下一個元素。
- ret = 5 cur1 = 4 cur2 = 2
第四輪循環：
- left[cur1] < right[cur2]，將 left[cur1] 這個元素加入到輔助數組中去，不要細 ret 的值。
- ret = 6 cur1 = 2 cur2 = 2
第五輪循環：
- left[cur1] < right[cur2]，與第一、第二、第三輪循環相同。此時 left 數組中的 1 個元素被與 right[cur2] 做逆序對，更新 ret 的值，并且將 right[cur2] 加入到輔助數組中去。
- ret = 8 cur1 = 1 cur2 = 2

處理剩余元素

如果是左邊出現剩余：
- 說明左邊剩下的所有元素都是比右邊元素大的，但是相較于方法二，逆序對的數量是沒有統計的。因此，我們需要統計 ret 的值。
- 設左邊數組剩余元素的個數為 left，ret += leave - (cur2 - 0)
如果是右邊出現剩余：
- 說明右邊剩下的所有元素都是比左邊元素大的，但是它們都是已經統計過的（我們以左邊的元素為基準的），因此不會產生新的逆序對，僅需歸并排序即可。

總結

整個過程只需將兩個數組遍歷一遍即可，時間復雜度依舊為 O(N)。

由上述過程我們可以得出方法一統計逆序對的關鍵點：

在合并有序數組的時候，遇到左數組當前元素 <= 右數組當前元素時，我們可以通過計算右數組已經遍歷過的元素的數量，快速求出去數組當前元素后面有多少個數比它大。

升序：找到該數之前，有多少個元素比我大

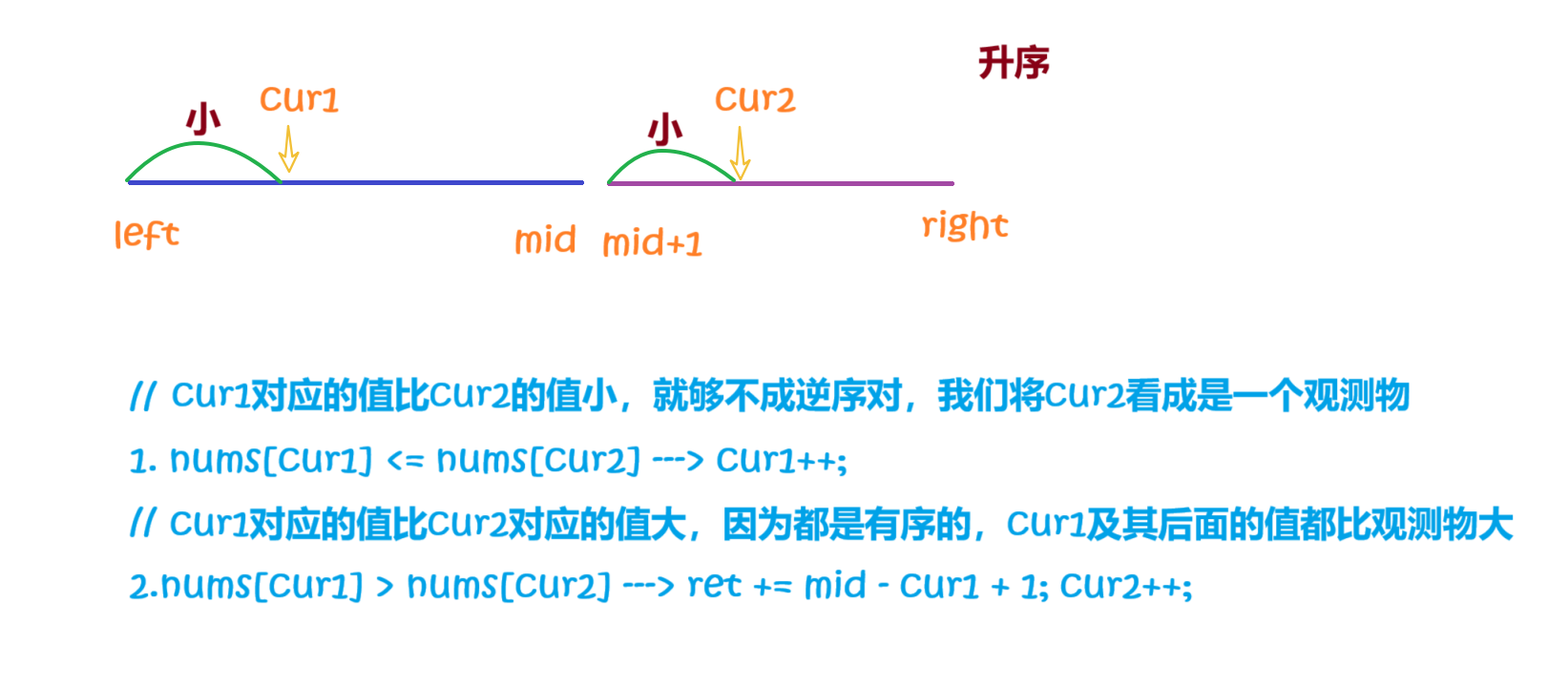
降序：找到該數之后，有多少個元素比我小

我們假設降序也是采用上面的策略，當 nums[cur1] > nums[cur2] 了，就需要 ret += [left, cur1]，然后cur1++后，如果還是nums[cur1] > nums[cur2]，cur2不動，就會導致前面的部分重復計算了！

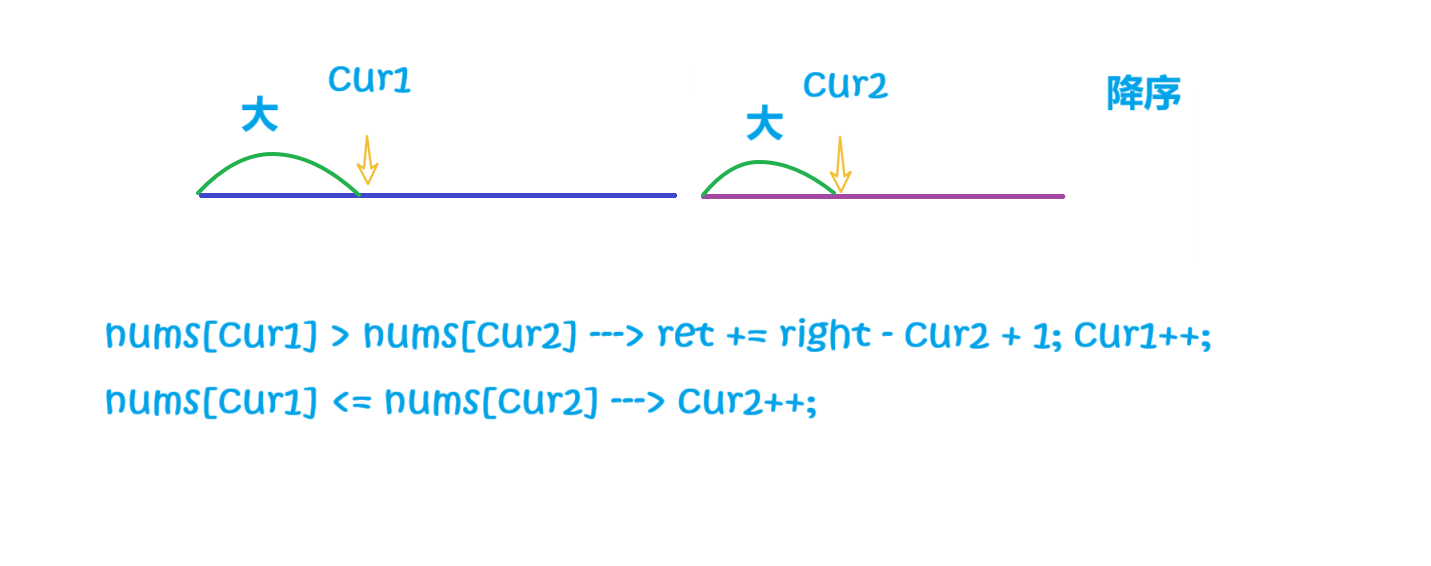
class Solution {
public:vector<int> tmp;int reversePairs(vector<int>& nums) {tmp.resize(nums.size());return MergeSort(nums, 0, nums.size() - 1);}int MergeSort(vector<int>& nums,int left, int right){if(left >= right) return 0;int ret = 0;int mid = left + ((right - left) >> 1);ret += MergeSort(nums, left, mid);ret += MergeSort(nums, mid + 1, right);//一左一右的個數int cur1 = left, cur2 = mid + 1, i = 0;while(cur1 <= mid && cur2 <= right){if(nums[cur1] <= nums[cur2]) tmp[i++] = nums[cur1++];else {ret += mid - cur1 + 1;tmp[i++] = nums[cur2++];}}while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; ++j) nums[j] = tmp[j - left];return ret;}
};

我們其實改成降序的版本也是ok的！（自行實現）

315. 計算右側小于當前元素的個數 - 力扣（LeetCode）

歸并排序中的逆序對統計

算法思路

在歸并排序中統計逆序對數量是一種經典的應用。此算法不僅要求總的逆序對數量，還需返回每個元素右邊有多少個元素比它小。由于元素下標在歸并過程中會變化，因此需要一個輔助數組來記錄下標。

算法流程

創建兩個全局數組：
- vector<int> index：記錄下標
- vector<int> ret：記錄結果
- index 用來與原數組中對應位置的元素綁定，ret 用來記錄每個位置統計出來的逆序對的個數。
countSmaller() 主函數：
- 計算數組 nums 的大小為 n。
- 初始化定義的兩個全局數組。
- 調用 mergeSort() 函數，并返回 ret 結果數組。
mergeSort() 函數：
- 修改全局變量 ret，統計出每個位置對應的逆序對的數量，并且排序。
- 無需返回值，因為直接對全局變量修改。
mergeSort() 函數流程：
- 定義遞歸出口：left >= right 時，直接返回。
- 劃分區間：根據 mid 將區間劃分為 [left, mid] 和 [mid + 1, right]。
- 統計左右兩個區間逆序對的數量。
- 合并左右兩個有序區間，并統計出逆序對的數量。

合并有序區間

創建兩個大小為 right - left + 1 的輔助數組：
- numsTmp：排序用的輔助數組。
- indexTmp：處理下標用的輔助數組。
初始化遍歷數組的指針：
- cur1 = left（遍歷左半部分數組）
- cur2 = mid + 1（遍歷右半部分數組）
- dest = 0（遍歷輔助數組）
循環合并區間：
- 當 nums[cur1] <= nums[cur2] 時：
  - indexTmp[dest] = index[cur1]
  - ret[index[cur2]] += nums[cur1] - nums[cur2] + 1
  - cur1++
- 當 nums[cur1] > nums[cur2] 時：
  - indexTmp[dest] = index[cur2]
  - cur2++
- dest++
處理剩余元素：
- 如果左邊有剩余，直接歸并。
- 如果右邊有剩余，直接歸并。
將輔助數組的內容替換到原數組中。

當前元素的后邊，有多少元素比我小？

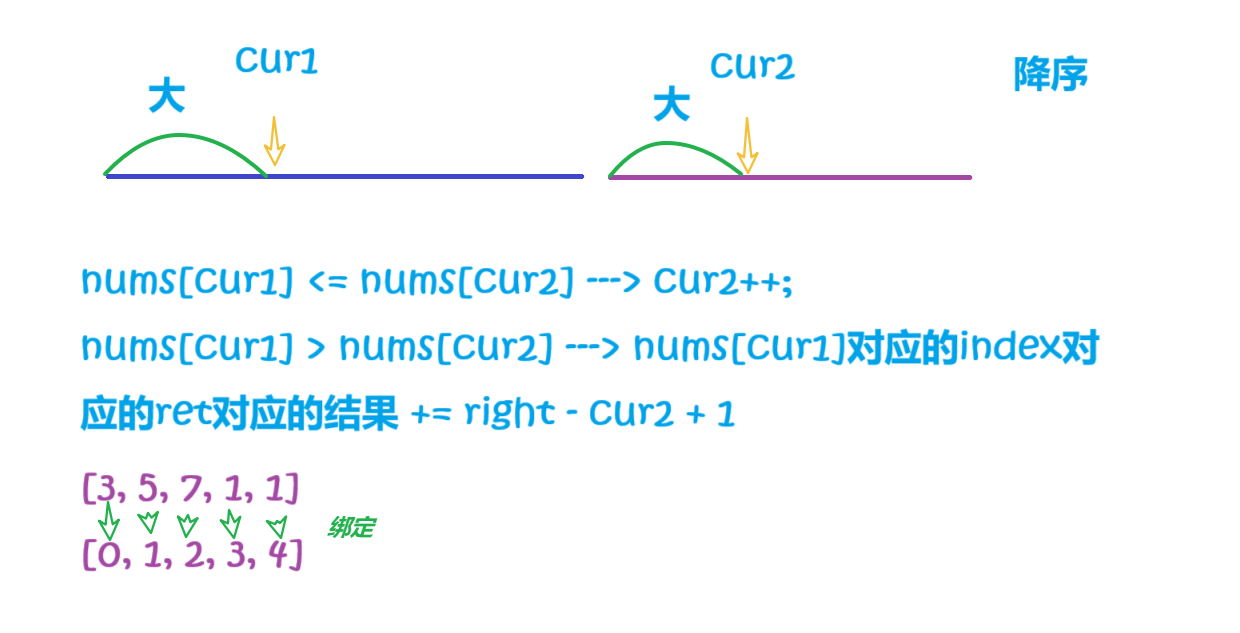
class Solution {
public:vector<int> index;vector<int> ret;int tmpNums[500010];int tmpIndex[500010];vector<int> countSmaller(vector<int>& nums) {int n = nums.size();ret.resize(n, 0);index.resize(n);for(int i = 0; i < n; ++i) index[i] = i;mergeSort(nums, 0, n - 1);return ret;}void mergeSort(vector<int>& nums, int left, int right){if(left >= right) return;int mid = left + ((right - left) >> 1);mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);int cur1 = left, cur2 = mid + 1, i = 0;while(cur1 <= mid && cur2 <= right){if(nums[cur1] <= nums[cur2]){tmpNums[i] = nums[cur2];tmpIndex[i++] = index[cur2++];}else{ret[index[cur1]] += right - cur2 + 1;tmpNums[i] = nums[cur1];tmpIndex[i++] = index[cur1++];}}while(cur1 <= mid){tmpNums[i] = nums[cur1];tmpIndex[i++] = index[cur1++];}while(cur2 <= right){tmpNums[i] = nums[cur2];tmpIndex[i++] = index[cur2++];}for(int j = left; j <= right; ++j){nums[j] = tmpNums[j - left];index[j] = tmpIndex[j - left];}}
};

493. 翻轉對 - 力扣（LeetCode）

歸并排序求解翻轉對數量

算法思路

大思路與求逆序對的思路一樣，就是利用歸并排序的思想，將求整個數組的翻轉對的數量，轉換成三部分：左半區間翻轉對的數量，右半區間翻轉對的數量，一左一右選擇時翻轉對的數量。重點就是在合并區間過程中，如何計算出翻轉對的數量。

與上個問題不同的是，上一道題我們可以一邊合并一邊計算，但是這道題要求的是左邊元素大于右邊元素的兩倍，如果我們直接合并的話，是無法快速計算出翻轉對的數量的。

因此我們需要在歸并排序之前完成翻轉對的統計。

示例過程

下面依舊以一個示例來模仿兩個有序序列如何快速求出翻轉對的過程：

假定已經有兩個已經有序的序列 left = [4, 5, 6] right = [1, 2, 3]。

用兩個指針 cur1 cur2 遍歷兩個數組。

對于任意給定的 left[cur1] 而言，我們不斷地向右移動 cur2，直到 left[cur1] <= 2 * right[cur2]。此時對于 right 數組而言，cur2 之前的元素全部都可以與 left[cur1] 構成翻轉對。
隨后，我們再將 cur1 向右移動一個單位，此時 cur2 指針并不需要回退（因為 left 數組是升序的）依舊往右移動直到 left[cur1] <= 2 * right[cur2]。不斷重復這樣的過程，就能夠求出所有左右端點分別位于兩個子數組的翻轉對數目。

由于兩個指針最后都是不回退的掃描到數組的結尾，因此兩個有序序列求出翻轉對的時間復雜度是 O(N)。

綜上所述，我們可以利用歸并排序的過程，將求一個數組的翻轉對轉換成求左數組的翻轉對數量 + 右數組中翻轉對的數量 + 左右數組合并時翻轉對的數量。

class Solution {
public: int tmp[50010];int mergeSort(vector<int>& nums, int left, int right){if(left >= right) return 0;int ret = 0;int mid = left + ((right - left) >> 1);ret += mergeSort(nums, left, mid);ret += mergeSort(nums, mid + 1, right);int cur1 = left, cur2 = mid + 1;while(cur1 <= mid){while(cur2 <= right && nums[cur2] >= nums[cur1] / 2.0) cur2++;if(cur2 > right) break;ret += right - cur2 + 1;cur1++;}cur1 = left, cur2 = mid + 1;int i = 0;while(cur1 <= mid && cur2 <= right){tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur2++] : nums[cur1++];}while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; ++j){nums[j] = tmp[j - left];}return ret;}int reversePairs(vector<int>& nums) {return mergeSort(nums, 0, nums.size() - 1);}
};