數據結構初階（12）排序算法—插入排序（插入、希爾）（動圖演示）

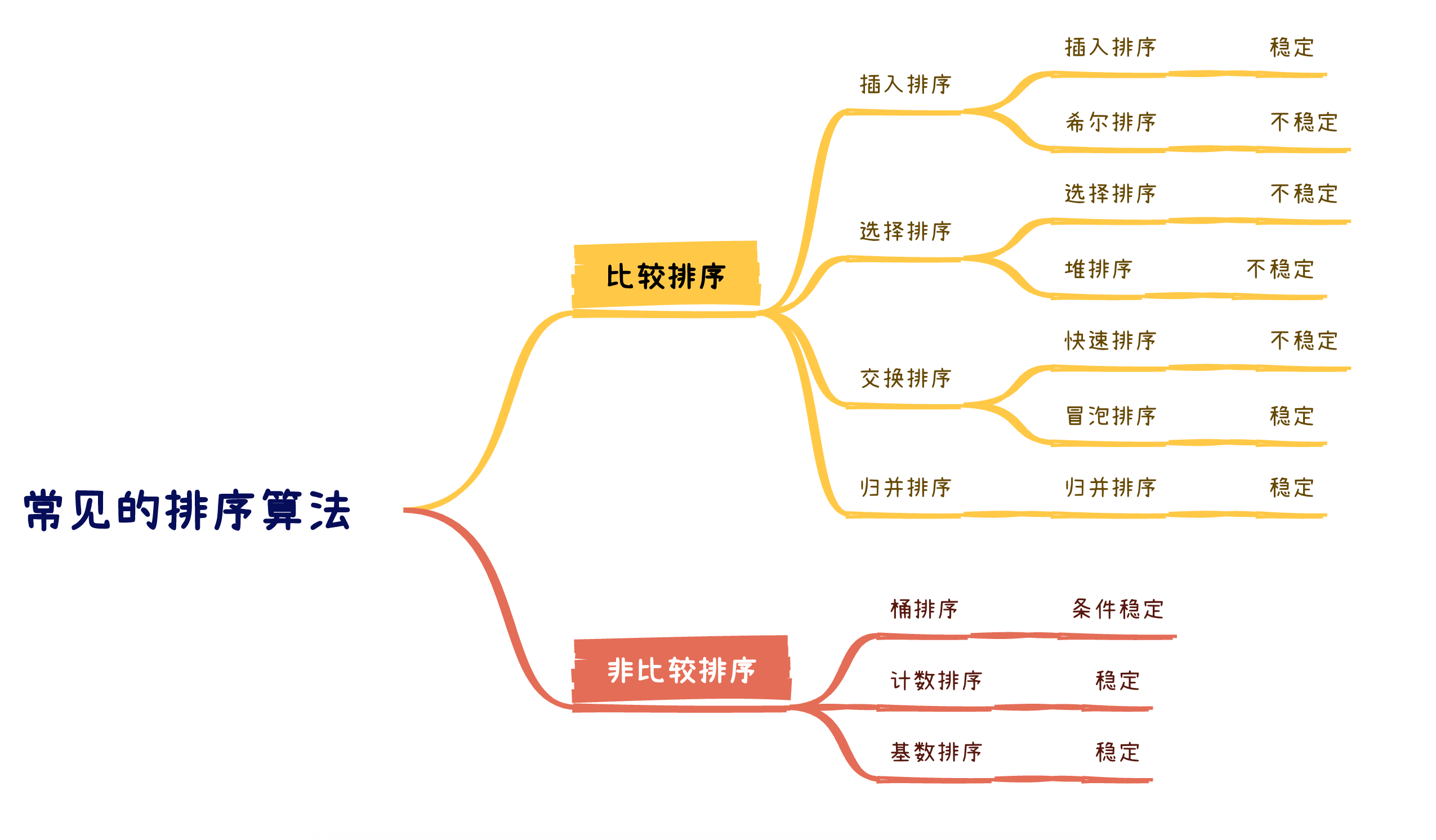
2. 常見排序算法的實現

2.0 十大排序算法

2.1 插入排序

2.1.1 基本思想

直接插入排序是一種簡單的插入排序法：

基本思想
把待排序的記錄按其關鍵碼值的大小逐個插入到一個已經排好序的有序序列中。
直到所有的記錄插入完為止，得到一個新的有序序列。

比 + 挪 (+ 插)

實際中我們玩撲克牌時，就用了插入排序的思想。

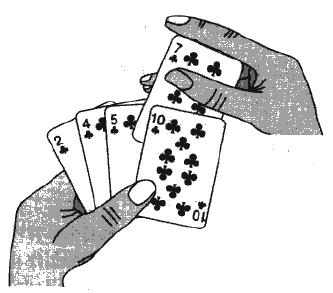
插入排序的思想：已經有一個有序序列，再新加入一個數據，將這個新加入的數據插入到合適的位置，保持整個序列依舊保持有序。

2.1.2 直接插入排序

基本邏輯

當插入第i(i>=1)個元素時，前面的array[0],array[1],…,array[i-1]已經排好序，此時用array[i]的排序碼與array[i-1],array[i-2],…的排序碼順序進行比較（依次進行比較），找到插入位置即將array[i]插入，原來位置上的元素順序后移。

動圖演示

算法步驟

1. 初始化：
將數組的第一個元素（arr[0]）視為已排序部分。
其余部分（arr[1]到arr[n-1]）視為未排序部分。
2. 遍歷未排序部分：
從i=1到n-1（n為數組長度)，依次取出arr[i]作為待插入元素 key（key?= a[i]）。
3. key從右向左比較，key較小則依次向后挪動路徑上的已排好序的數據
初始化 j = i－1（即已排序部分的最后一個元素)。
如果 key < arr[j]，則arr[j]向后移動一位（arr[j+1] = arr[j]），并繼續向左比較（j--）
直到找到arr[j] ≤ key或j<0（即已比較完所有已排序元素)。
4. 將key插入到正確位置：
將key 插入到arr[j+1]的位置。（arr[j+1] = key）
5. 重復上述過程，直到所有未排序元素都被處理。

優化思路：

二分查找優化：在已排序部分使用二分查找快速找到插入位置，減少比較次數
（但仍需相等的挪動次數，優化程度有限，代碼變復雜，不建議）

終止條件：

外層循環終止：當所有未排序元素（i 從 1 到 n-1）都被處理完畢時，排序結束。
內層循環終止：
當 j < 0（即已比較完所有已排序元素）。
或 arr[j] ≤ key（找到正確插入位置）。

代碼實現

建議排序算法部分的代碼，先實現單趟，再實現整體——更好控制。

一上來就直接進行排序整體控制——不好控制。

先考慮單趟——把一個數插入一個有序數組 [0, end] end+1 。

end的起始位置在0，然后依次把后面一個元素當作end+1插入前面的有序數組

1. 先考慮單趟
先保存待插入數據，再把前面的數據后挪（否則數據被覆蓋）。
注意比較邏輯，將算法控制為一個穩定算法。
兩個循環結束條件，循環結束后插入tmp。

2.再考慮整體
每趟外循環給end、tmp賦值。
end的結束位置在n-2，外循環的結束條件是i < n-1（若 i < n 會越界訪問）。

//(直接)插入排序
void InsertSort(int* a, int n)
{//2.再考慮循環for (int i = 0; i < n - 1; i++)	//若i<n則會導致插入一個隨機數-858993460作首元素{//1.先考慮單趟——把一個數插入一個有序數組//往[0, end]的有序數組中插入end+1//每趟外循環給end賦值——end的起始位置在0int end = i;//然后依次把后面一個元素當作end+1插入前面的有序數組——end的結束位置在n-2int tmp = a[end + 1];	//先保存待插入數據，再把前面的數據后挪（否則數據被覆蓋）while (end >= 0)		//end小于0，循環比較截止，tmp插入到end后面{//如果tmp較小if (tmp < a[end]){//排好的數據就往后挪，給tmp騰位置a[end + 1] = a[end];//迭代--end;}//如果tmp較大或相等，前排數據就不后挪——>就可以做到穩定else{break;			//tmp較大或相等，循環比較截止，tmp插入到end后面}}//tmp比某值大(相等) / 比全部小（end = -1），都tmp插入到end后面a[end + 1] = tmp;}
}

代碼測試。

也可以在監視中觀察每一趟排序的過程。

性能分析

時間復雜度——簡單粗暴，兩層循環就是 O(N^2)——錯（不能只看循環次數）

最壞情況：逆序——1，2，3，......，n-1——>合計O( N^2 )

最好情況是多少：順序有序或者接近有序 ?O(N)

有序為什么不是O(1)——沒有排序能做到O(1)，最好就是O(N)——極限情況下。

有序也得O(N)比完才知道有序。

正常最快就是O(N*logN)。

時間復雜度：
情況時間復雜度說明
最優情況（已排序數組） O(N) 每趟只需比較一次，無需移動元素
最壞情況（完全逆序） O(N^2) 每次插入需比較和移動所有已排序元素
平均情況（隨機數組） O(N^2) 平均需要 (N^2) / 4次比較和移動
空間復雜度：
空間復雜度：需常數額外空間O(1)。
穩定性：
穩定?

情況	時間復雜度	說明
最優情況（已排序數組）	O(N)	每趟只需比較一次，無需移動元素
最壞情況（完全逆序）	O(N^2)	每次插入需比較和移動所有已排序元素
平均情況（隨機數組）	O(N^2)	平均需要 (N^2) / 4次比較和移動

特性總結

直接插入排序的特性總結：

元素集合越接近有序，直接插入排序算法的時間效率越高。
時間復雜度：O(N^2)。
空間復雜度：O(1)，它是一種穩定的排序算法。
穩定性：穩定。

2.1.3 希爾排序

基本邏輯（算法步驟）

希爾排序是以人名命名的。希爾發現插入排序雖然在O(N^2)這個量級，但是插入排序顯著地快，因為插入排序具有很強的適應性，幾乎每次都不是最壞，甚至都還不錯。

而且要是有序或者接近有序，插入排序能接近線性時間復雜度——O(N)。

希爾排序就是讓數據接近有序的插入排序。

故而希爾排序把排序分為兩步：

1. 預排序：目標就是讓數據接近有序——gap > 1
分組預排插入——目標：讓在前面的大的數據更快換到后面的位置，在后面的小的數據更快地換到前面的位置。
2. 全排序：目標就是讓數據全部有序——gap == 1

希爾排序法又稱縮小增量排序法（遞減增減排序）。

希爾排序是插入排序的一種更高效的改進版本。但希爾排序是非穩定排序算法。

希爾排序是基于插入排序的以下兩點性質而提出改進方法的：

插入排序在對幾乎已經排好序的數據操作時，效率高，即可以達到線性排序的效率；
但插入排序一般來說是低效的，因為插入排序每次只能將數據移動一位；

希爾排序法的基本思想是：

基本邏輯
先選定一個整數gap，把待排序文件中所有記錄分成個組。
所有距離為gap的記錄分在同一組內。（gap也相當于組數）
然后對每一組內的記錄進行插入排序。（組內插入排序）
然后取gap = gap / 2，重復上述分組和排序的工作。
當到達gap?= 1 時，所有記錄在同一組內，進行最后一次插入排序。

誤區
gap=1并不是說1個元素一組，而是說相隔為1的所有元素組成一組，即整個數組
可以認為gap代表組數：
gap越小，組數越少
gap越大，分組越多

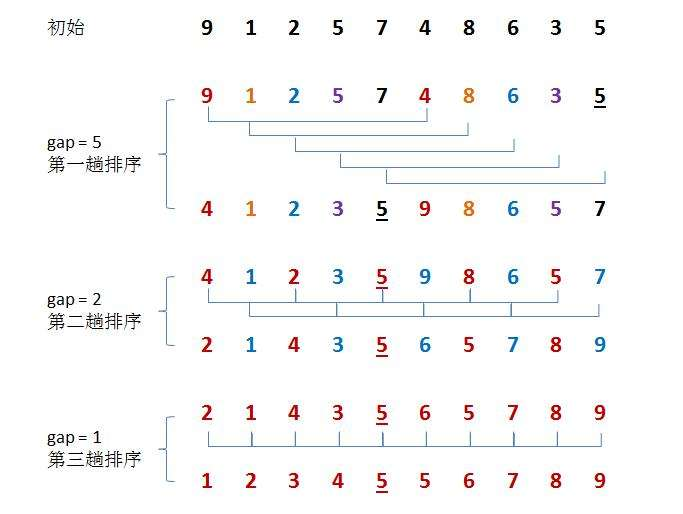
希爾排序的優勢
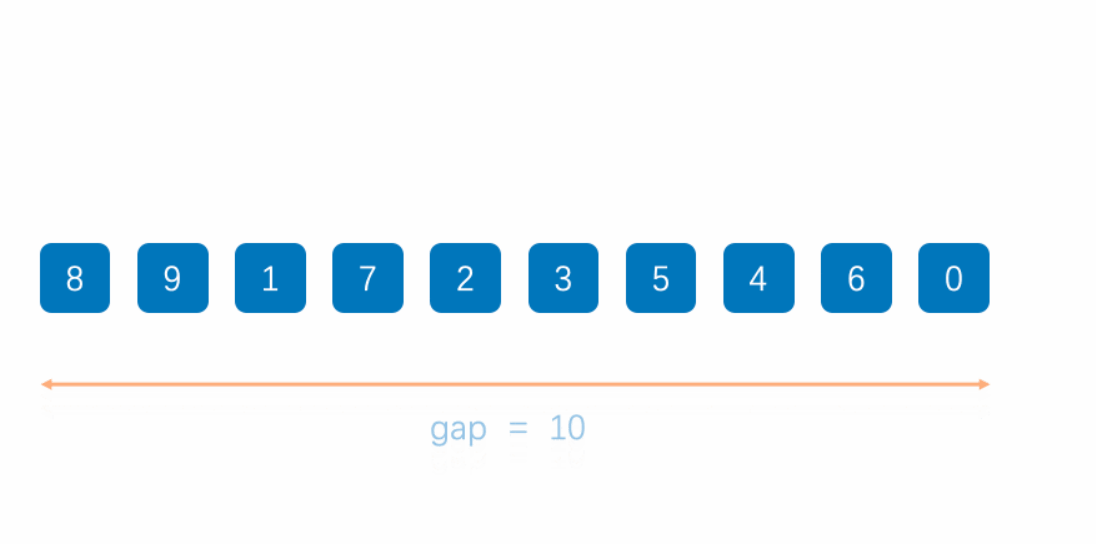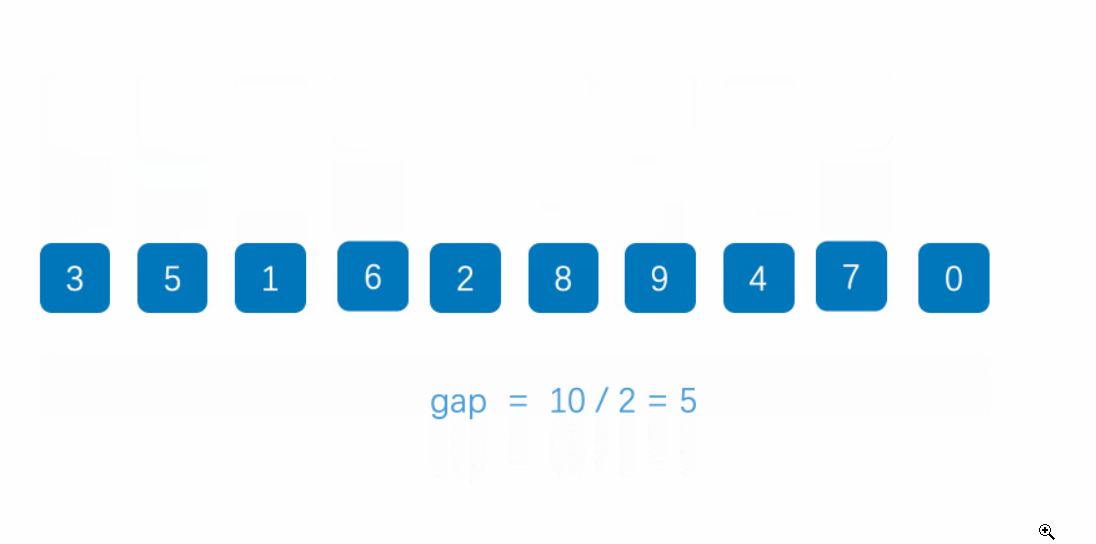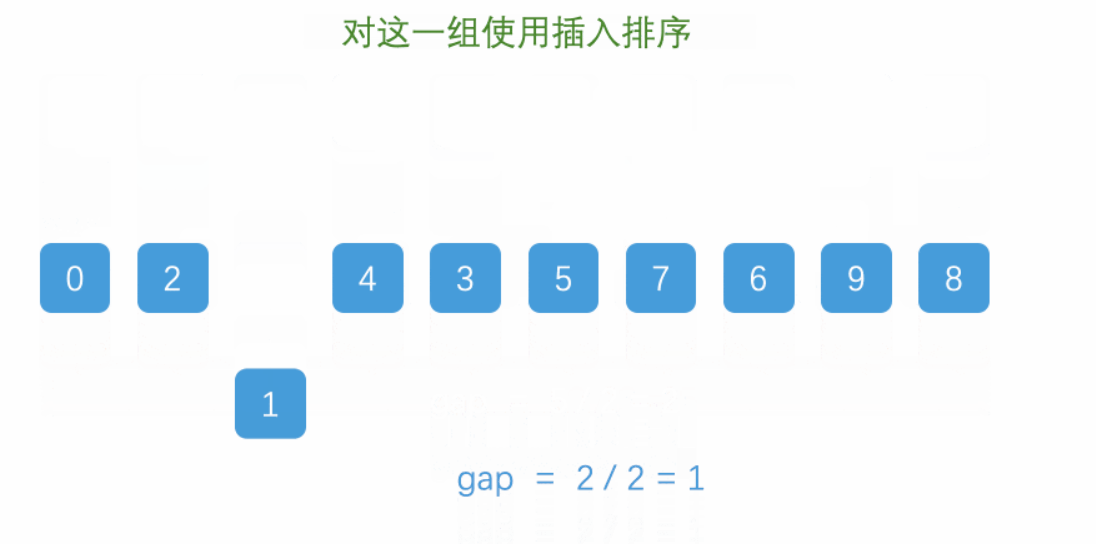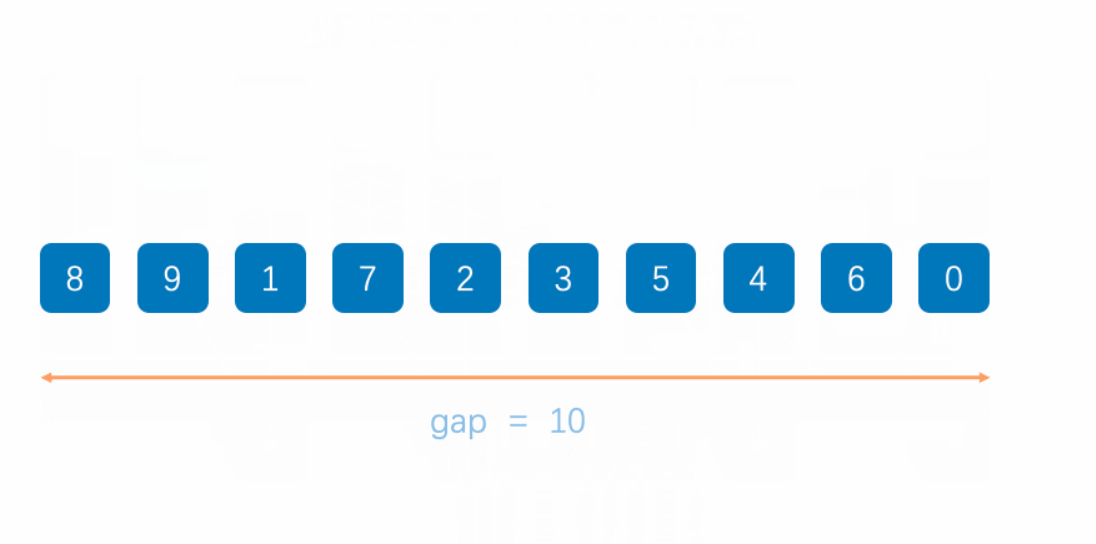
第一趟，gap == 5，這樣同組內的數據，挪動一次，就能相當于外面的5步。
第二趟結合第一趟，在最開頭的數據9，挪動3次就來到最后了。

動圖演示

代碼實現

排序算法先完成單趟，再實現整體控制。

通過控制起始位置，完成不同顏色組別的插入排序的控制。

3層循環，很多人很懷疑這里的執行效率。

實際上考慮時間復雜度不能只看循環層數，主要看的還是算法思想。

每趟：3層循環→優化成2層循環。（效率沒有差別）

1. 先考慮單趟
某一個gap值
中層for循環，遍歷end = [0,n-gap)，end是已排好序的最后一個元素
兩次循環遍歷的end = i，是兩個不同的組。
組內執行a[end+gap]這個數的直接插入排序，過程中end每次往前迭代gap個元素。
2. 再考慮整體
每趟給不同的gap值。
最后一趟gap==1，全排序。

//希爾排序
void ShellSort(int* a, int n)
{//給gap賦值數組長度——1個數據一組int gap = n;//3.多次逐次增加精度的預排序——>每一次都更接近有序while (gap > 1){//迭代——log2(N)次、log3(N)次——最外層while循環時間復雜度//gap /= 2;//選擇除2：但是這樣會導致預排序次數過多，就選擇除3//選擇除3：但不能保證最后為1，就手動+1gap = gap / 3 + 1;//2.一組的直接插入排序 和 全數組預分組排序for (int i = 0; i < n - gap; i++)        //留出一個n-gap的空間{//1.一個數tmp的直接插入排序//控制end 元素的位置 —— 一開始在0int end = i;//控制插入元素的位置 —— end+gap//保存在臨時變量中，避免挪動覆蓋int tmp = a[end + gap];//直接插入排序while (end >= 0){//比較if (tmp < a[end]){//1.挪動a[end + gap] = a[end];//2.end往前跳end -= gap;}else{break;}}//賦值a[end + gap] = tmp;}//PrintArray(a, n);    每個gap，預排序后都打印觀察一下效果——>越來越有序}
}

代碼測試。

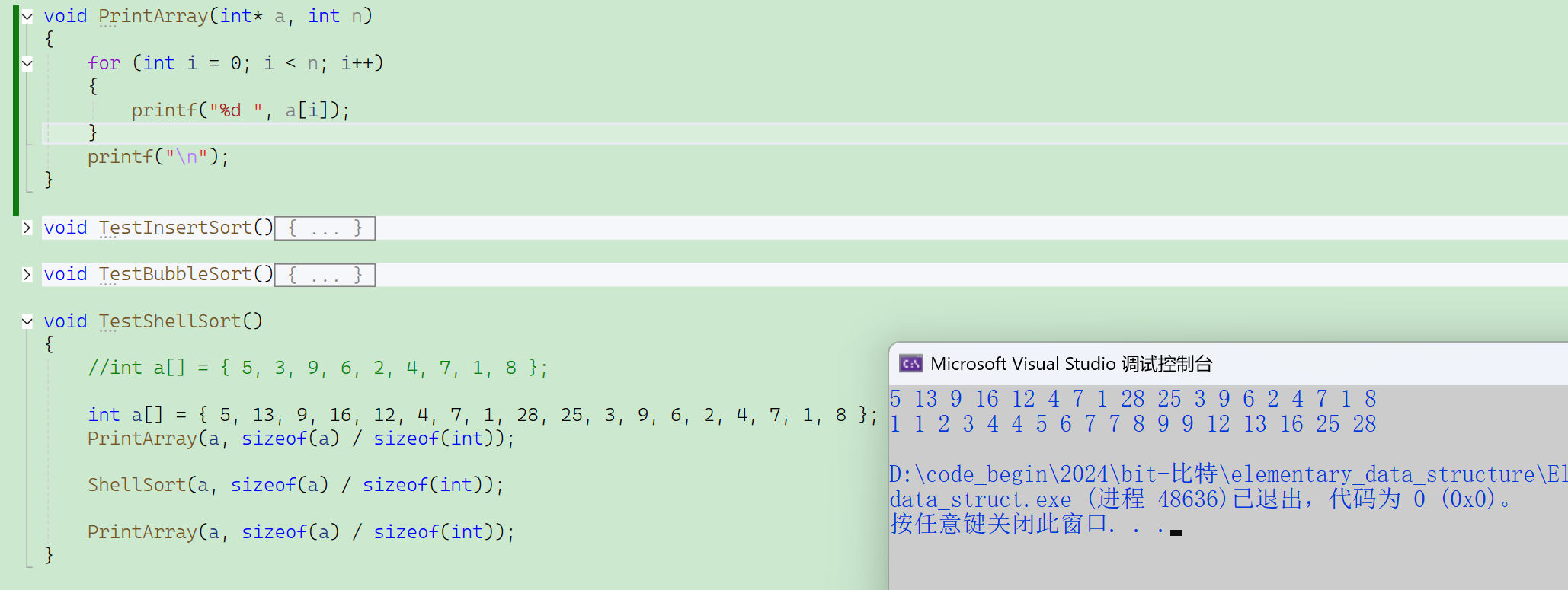
這樣一共3層循環（優化后），效率受到一些質疑。

性能分析

時間復雜度：
本實現的 gap / 3 + 1 序列平均性能優于傳統的 n / 2 序列
最壞情況仍為O(n2)，但實際運行中很少出現
當數據部分有序時，性能接近O(n log n)
空間復雜度：
僅使用常數個臨時變量 O(1)
穩定性：
不穩定

簡單分析時間復雜度：

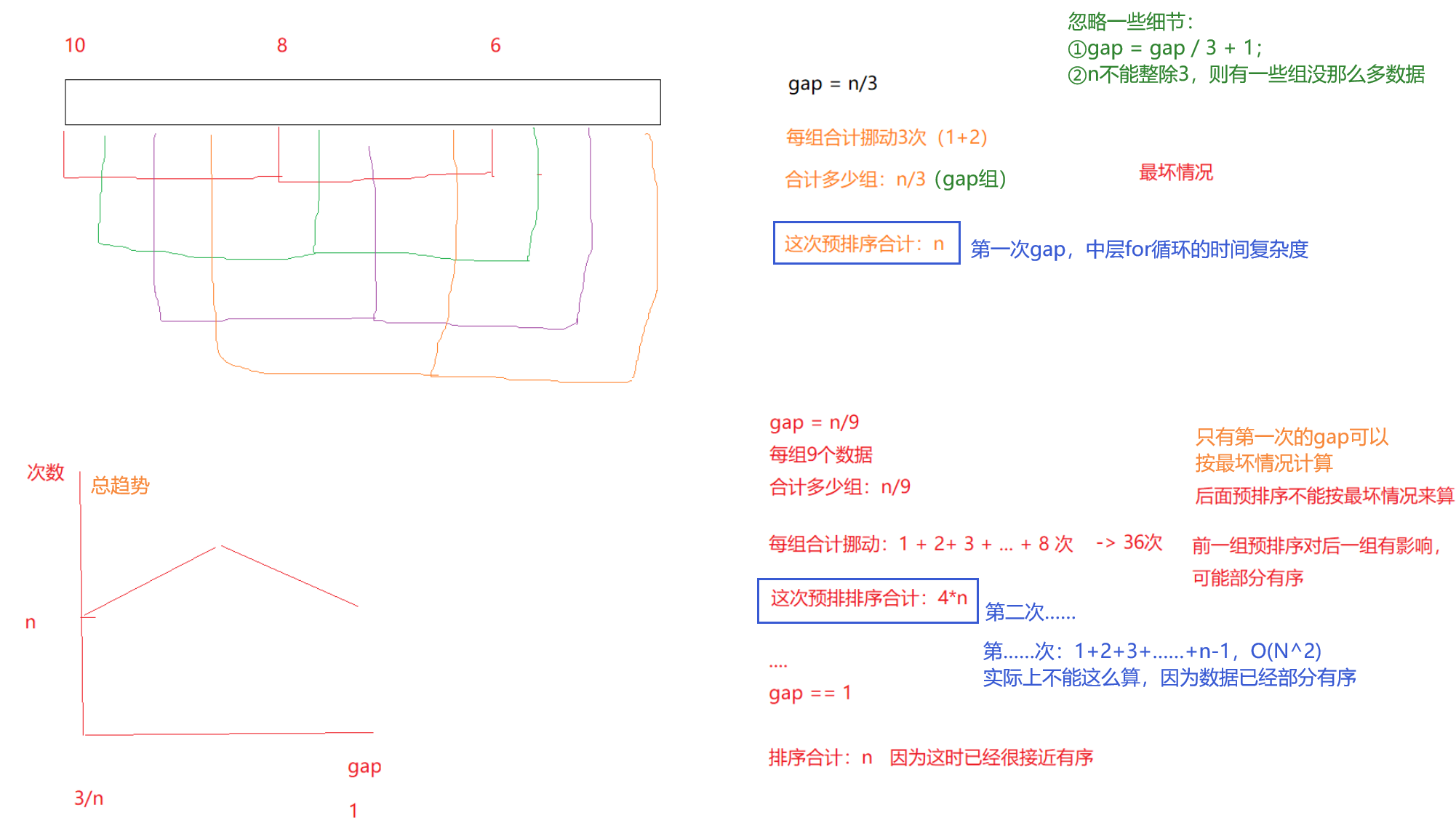
外層while循環的時間復雜度——gap迭代次數。

log2(N)次、log3(N)次。

中層for循環的時間復雜度——第一個gap值下，基本上是n次，最后一個gap值下，基本上是n次，中間是一個變化的過程。

N——>a*N((a>1) ——>N。

總的時間復雜度

log3(N) * N——>log3(N) * a*N?(a>1) ——>log3(N) * N。

總結：比log3(N) * N大，大約是 N ^ 1.3 = N^(0.3) * N。

對數增長 VS 指數增長。

所以嚴格來說，希爾排序時間復雜度比堆排、快排慢一個檔。

但是只是在10萬，100萬慢，1000萬個數據希爾比堆排快。

因為時間復雜度只反映一個最壞的情況，時間復雜度看的是最壞，如果它有多個項，它看的是影響最大的那個項，看的是它的量級。

但是很多具體細節會影響具體時耗——具體細節：

① 具體的算法思想：會不會每次都最壞（例子：插入 VS 冒泡）。

② 算法的其他消耗：比如數據量足夠大時，建堆的時耗O(N)也不小。

③ 不同的數據樣本：插入排序在接近有序時，效率高于堆排序。
（處理隨機數據當然堆排序好用）

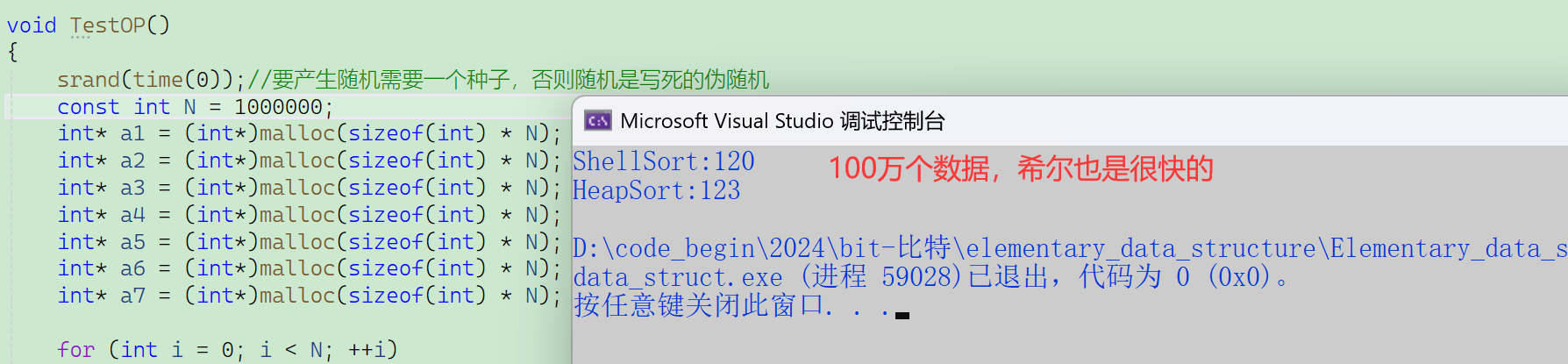
性能測試

void TestOP()
{srand(time(0));//要產生隨機需要一個種子，否則隨機是寫死的偽隨機const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);    //創建7個無序數組，每個數組10萬個元素int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();                         //隨機生成10萬個元素，給7個數組a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();    //系統啟動到執行到此的毫秒數InsertSort(a1, N);int end1 = clock();      //系統啟動到執行到此的毫秒數int begin7 = clock();//BubbleSort(a7, N);int end7 = clock();int begin3 = clock();//SelectSort(a3, N);int end3 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();//int begin5 = clock();//QuickSortNonR(a5, 0, N - 1);//int end5 = clock();//int begin6 = clock();//MergeSortNonR(a6, N);//int end6 = clock();printf("InsertSort:%d\n", end1 - begin1);//printf("BubbleSort:%d\n", end7 - begin7);printf("ShellSort:%d\n", end2 - begin2);//printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);//printf("QuickSort:%d\n", end5 - begin5);//printf("MergeSort:%d\n", end6 - begin6);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{//TestInsertSort();//TestBubbleSort();//TestShellSort();//TestSelectSort();//TestQuickSort();//TestMergeSort();//TestCountSort();TestOP();//MergeSortFile("sort.txt");return 0;
}

測試結果——10萬個數據下：

（gap /= 2 效率大概在12ms左右，比gap = gap/3+1稍微慢一些）

希爾排序的效率接近與堆排序O(N*logN)。

希爾排序遠優于直接選擇排序。

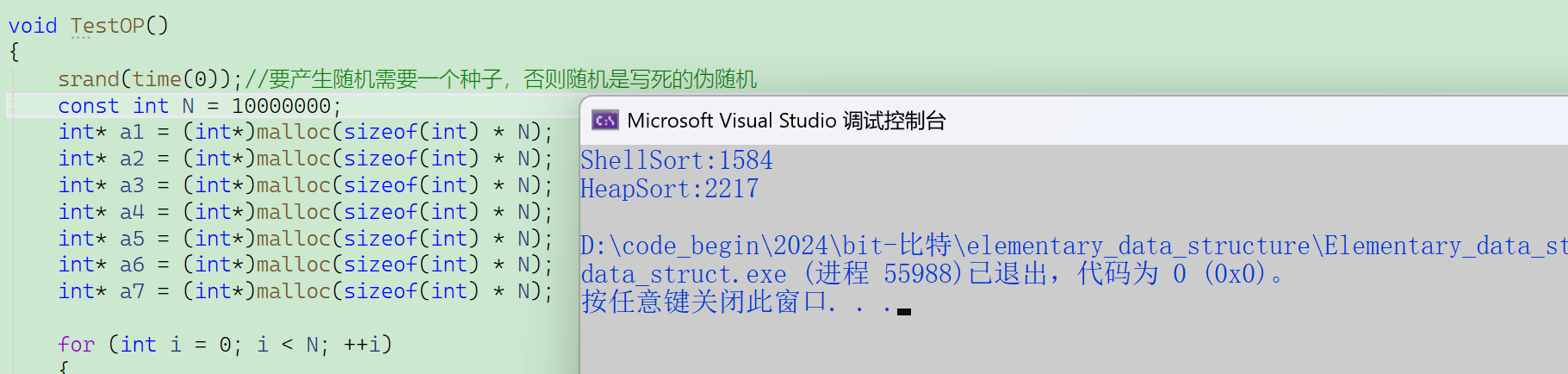
1000萬個數據，希爾排序的效率就已經要優于堆排序了。

（時間復雜度只代表一個大概的量級，具體快慢還取決于一些細節因素）

n→∞，希爾排序的時間復雜度→O(N * (logN)^2)，相較與堆排序的O(N^log^N)。

大概而言，希爾排序的時間復雜度在O(N^1.3)。

特性總結

希爾排序的特性總結：

1. 希爾排序是對直接插入排序的優化。
2. 當gap > 1時都是預排序，目的是讓數組更接近于有序。當gap == 1時，數組已經接近有序的了，這樣就會很快。這樣整體而言，可以達到優化的效果（性能測試的對比）。
3. 希爾排序的時間復雜度不好計算，因為gap的取值方法很多，導致很難去計算，因此在好些樹中給出的希爾排序的時間復雜度都不固定：
《數據結構(C語言版)》--- 嚴蔚敏

《數據結構-用面相對象方法與C++描述》--- 殷人昆

4. 穩定性：不穩定。