寫在前面：不建議觀看，會爛尾的

1.馬氏鏈：狀態空間指的是隨機變量的取值范圍，xi稱為一個狀態，應用背景在現在的條件下下一狀態發生的概率，比如退火，他的條件概率可化簡為：

且n+m時刻的概率只與間隔時間m和狀態i，j有關即：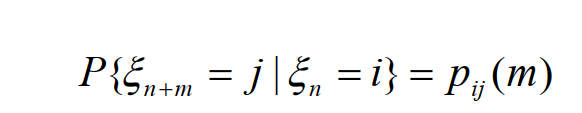

這個新概率叫m步轉移概率，ij當行列就有m步為變量的轉移矩陣。顯然遍歷整個狀態空間當然概率和是1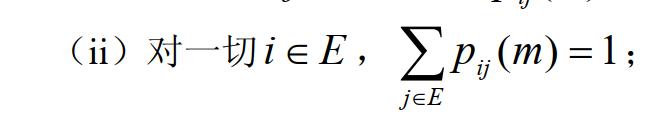

特殊的如果移動0步，規定i=j時概率是1，不相等為0

那該如何知道概率p呢？可以由過往經驗如退火算法，也可以由數據規律：即找出所有的可能的狀態取值，如何列出這些取值之間的跳轉如00，01，10，11.通常認為步數是1，在步數是1的情況下找出所有跳轉次數，然后認準是從哪里開始跳的，如果要近似00跳轉的概率則找出所有從0開始跳的概率和當分母即00，01。分子是00即可。

其他還有很多定理和衍生概率，這里就不介紹了只是簡單講講而已。應用馬爾可夫鏈的計算方法進行馬爾可夫分析， 主要目的是根據某些變量現在的情況及其變動趨向，來預測它在未來某特定區間可能產生的變動，作為提供某種決策的依據。

2.蒙特卡洛：
又稱隨機抽樣或統計試驗法，基本思想是頻率代替概率，算術平均代替期望（其實就是用數據代替理論推導中未知的值，而這些未知的值往往在概率論中有公式）。

通常來講，先從實際問題抽象出隨機變量X，通過試驗得到算術平均值當期望（考研時學過根據數定律數據要夠大且每次都是獨立同分布），后面也相應可以算出置信度和誤差（降低方差和增大N都可以降低誤差）。

效率概念：等于方差*觀察子樣花費時間

優點：受限小，收斂速度和維數無關但是慢因此高維情況使用效果好，誤差容易確定但是誤差確定是在給定置信度的情況下計算的

3.matlab語法：

矩陣操作：缺省y（：，：）表示取全部，前行后列，1：2：8表示第1到第8，步長2

矩陣變換：x=x（：）；默認列向量，因此要行向量得轉置，拉成列向量時先第一列后第二列按列放數據

矩陣拼接：拉成列向量，矩陣操作后面加的是圓括號，矩陣給出是方括號，因此要拼接是【x y】

水平拼接用逗號或者空格都行，要增加行的話就得用；分隔。

inf為無窮大常量

4.這些優化算法核心是跳出方向的設置而不是跳出條件的判斷，目前狀態的領域應該怎么確定。而模擬退火的則是模擬退火通過一個預先定義的“鄰域函數”，從當前解的“鄰近”解中隨機選擇一個候選解，作為可能的“跳出方向”。 這我覺得是最關鍵的，這個領域是人為定義的擾動，比如在下面的TSP問題中就有一個規則。這個規則是因問題而定的，和退火系數起始問題共同影響著最后出來的結果質量。

TSP路徑反轉形成新解。

5.遺傳算法

模擬自然界，初始群體的產生、求每一個體的適應度、根據適者生存的原則選擇優良個體。

通過隨機交叉其染色體的基因并隨機變異某些染色體的基因后生成下一代群體，按此方法使群體逐代進化。

需要確定種群數量，遺傳代數，交叉率（一般是1），變異率。

與模擬退火不同，假如種群數量是500，那就得先給出500條路徑（初始解）（TSP問題）作為父代，然后若是求最小值，則min（500個父代）這個min函數叫做適應度函數，用于評估優秀個體。

然后從里面選兩個個體（解）出來劃定第i個位置為交叉點，交叉點前面不懂后面交換。交叉方式多種多樣這里只是一種。然后還可以跳出個別點交換位置叫做變異。

500個父代每兩個湊組交換生成子代，再在子代中按照變異率選個別個體變異后生成變異體，變異體，子代，父代中按照適應度函數選出優秀種群作為新父代。

6.禁忌搜索算法

禁忌搜索算法用一個禁忌表記錄下已經到達過的局部最優點，在下一次搜索中，利用禁忌表中的信息不再或有選擇地搜索這些點

是組合優化算法的一種，組合優化：是一種大的學科類別

核心特征：?離散決策、有限解空間、目標是最小化或最大化某個目標函數。

由于上述都是用距離描述鄰域，在組合優化則有一個更高層次的抽象概念鄰域：

D 表示決策變量的定義域， F表示可行解區域， F 中的任何一個元素稱為該問題的可行解， f 表示目標函數。

候選集合：

禁忌表：禁忌表中的兩個主要指標是禁忌對象和禁忌長度，，一般是給禁忌對象x一個禁忌長度t，當迭代次數超過t次時禁忌對象x被解禁。

評價函數：評價函數是侯選集合元素選取的一個評價公式，侯選集合的元素通過評價函數值
來選取。以目標函數作為評價函數是比較容易理解的。目標值是一個非常直觀的指標，但有時為了方便或易于計算，會采用其他函數來取代目標函數。

特赦規則：字面意思

記憶頻率信息：一個最優值出現的頻率輔助判斷是否停止迭代或解禁元素

P類問題是可以找到一個能在多項式時間內解決它的算法。

NP問題是指可以在多項式的時間里驗證一個解的問題。NP問題的另一個定義是，可以在多項式的時間里猜出一個解的問題。