機器學習第四課之決策樹

簡介

一.決策樹算法簡介

二.?決策樹分類原理

1.ID3算法

1.1 熵值

1.2?信息增益

1.3 案例分析

?編輯?2.C4.5

2.1?信息增益率

?2.2.案例分析

?3.CART決策樹

3.1基尼值和基尼指數

3.2案例分析

三、決策樹剪枝

四、決策樹API

?五、電信客戶流失

?六、回歸樹

七.?回歸樹API

簡介

????????決策樹的核心邏輯就像我們日常生活中的選擇過程：從一個初始問題出發，根據不同的答案走向不同的分支，最終抵達一個明確的結論。這種 “層層設問、逐步拆分” 的思路，讓它成為機器學習中最容易理解和解釋的模型之一，哪怕是沒有太多算法基礎的人，也能快速看懂它的決策路徑。

一.決策樹算法簡介

決策樹：

決策樹通過對訓練樣本的學習，并建立分類規則，然后依據分類規則，對新樣本數據進行分類預測，屬于有監督學習。

監督學習：就是對于x特征有y結果

無監督學習：沒有y結果

是?種樹形結構，本質是?顆由多個判斷節點組成的樹
其中每個內部節點表示?個屬性上的判斷，
每個分?代表?個判斷結果的輸出，
最后每個葉節點代表?種分類結果。

?核心：所有數據從根節點一步一步落到葉子節點。

怎么理解這句話？通過?個對話例?

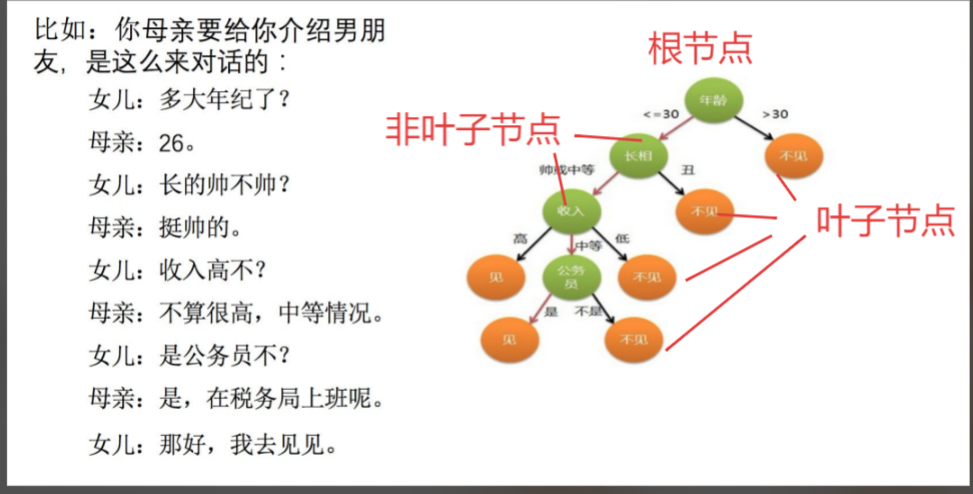
?決策樹分類標準：

ID3算法
C4.5算法
CART決策樹

二.?決策樹分類原理

1.ID3算法

1.1 熵值

????????物理學上，熵 Entropy 是“混亂”程度的量度。系統越有序，熵值越低；系統越混亂或者分散，熵值越?。

熵值計算公式：

? $H(U)=E\left [ -logp_{i} \right ]=-\sum_{i=1}^{n}p_{i}logp_{i}$

?A 集合:[1, 1, 1, 1, 1, 1, 1, 1, 2, 2]

B 集合:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

A 集合熵值:? $-2/10*\log 2(2/10)-8/10*\log 2(8/10) = 0.722$

B 集合熵值:? $-1/10*\log 2(1/10)*10 = 3.322$

1.2?信息增益

????????信息增益：以某特征劃分數據集前后的熵的差值。熵可以表示樣本集合的不確定性，熵越?，樣本的不確定性就越?。因此可以使?劃分前后集合熵的差值來衡量使?當前特征對于樣本集合D劃分效果的好壞。

信息增益 = entroy(前) - entroy(后)

?信息增益表示得知特征X的信息?使得類Y的信息熵減少的程度

1.3 案例分析

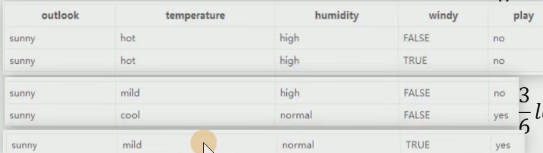
現在有個表格

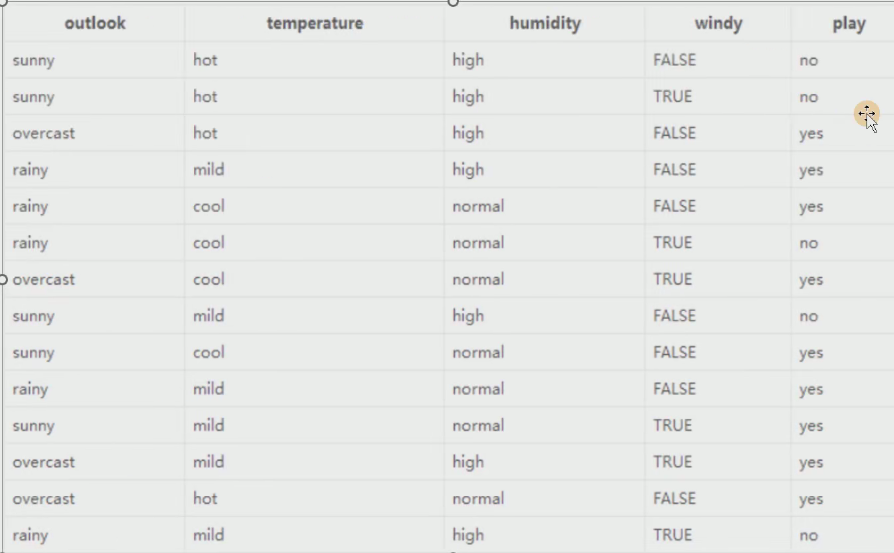
表格中顯示在 Outlook、temperature、humidity、windy的影響下到底出不出去的情況。

?第一遍遍歷：

1. 標簽（結果是否外出打球）的熵（類別熵）：
????????14 天中，9 天打球，5 天不打球，熵為：

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad-\frac{9}{14}log_{2}\frac{9}{14}-\frac{5}{14}log_{2}\frac{5}{14}=0.940$

import math
result = -9/14*math.log(9/14, 2) - 5/14*math.log(5/14, 2)

?2. 基于天氣的劃分

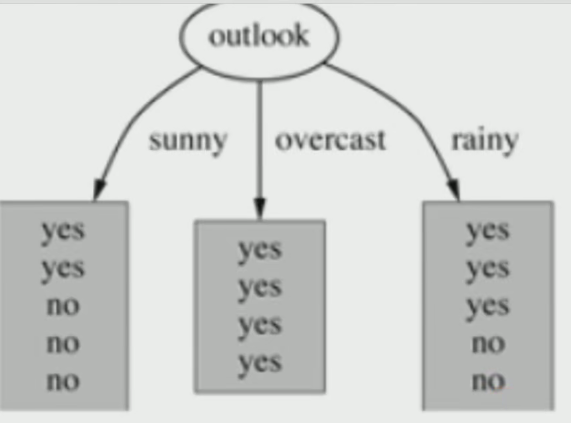
?屬性熵：
晴天【5 天】的熵：

? $-\frac{2}{5}log_{2}\frac{2}{5}--\frac{3}{5}log_{2}\frac{3}{5}=0.971$

Overcast（陰天）【4 天】的熵：

$-\frac{5}{5}log_{2}\frac{5}{5}=0$

雨天【5 天】的熵：?

$-\frac{3}{5}log_{2}\frac{3}{5}-\frac{2}{5}log_{2}\frac{2}{5}=0.971$ ?

整體天氣都熵值：

$\frac{5}{14}*0.971+\frac{4}{14}*0+\frac{5}{14}*0.971=0.693$

?則信息增益為：0.940-0.693=0.247

3. 基于溫度的劃分

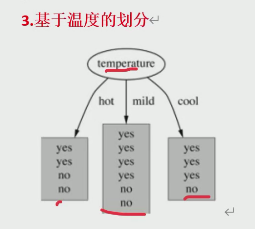
Hot【4 天】的熵：

$-\frac{2}{4}log_{2}\frac{2}{4}-\frac{2}{4}log_{2}\frac{2}{4}=1.000$

Mild【6 天】的熵：?

$-\frac{4}{6}log_{2}\frac{4}{6}-\frac{2}{6}log_{2}\frac{2}{6}=0.918$ ?

Cool【4 天】的熵：?

$-\frac{3}{4}log_{2}\frac{3}{4}-\frac{1}{4}log_{2}\frac{1}{4}=0.811$ ?

?熵值計算：

$4/14*1 + 6/14*0.918 + 4/14*0.811 = 0.911$

信息增益為： $0.940 - 0.911 = 0.029$

?4. 基于濕度的劃分

5. 基于風的劃分

?以上兩個按照步驟就可以算出來

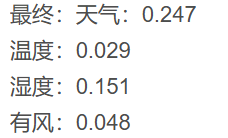
最終：天氣：0.247
溫度：0.029
濕度：0.151
有風：0.048
顯然，信息增益最大的是：天氣 > 濕度 > 有風 >溫度

所有就以天氣為根節點 ,然后天氣下面有三種情況sunny、rainy、overcast，然后再對剩下的溫度、濕度、有風三種情況求熵值然后求信息增益，找出各自的根節點

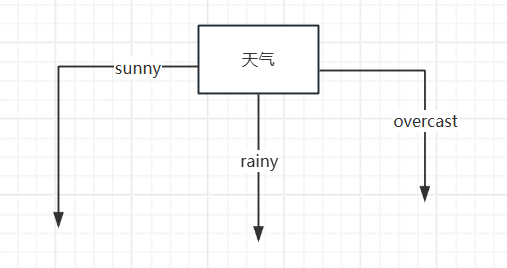
?例如在sunny相同下求根節點，以此類推

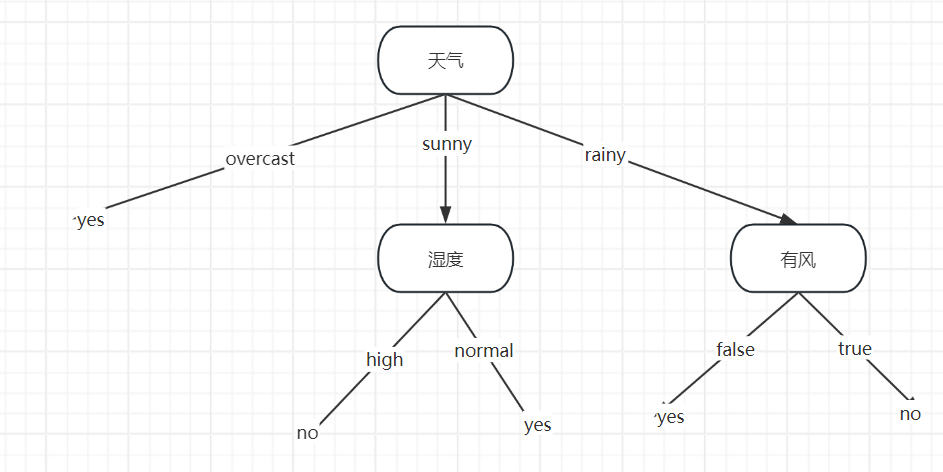
?最終得到的結果如下圖：

?2.C4.5

2.1?信息增益率

息增益率：特征 A 對訓練數據集 D 的信息增益比 $g_R(D,A)$ ，為其信息增益 $g(D,A)$ 與訓練數據集 D 的經驗熵 $H(D)$ 之比：

$g_R(D,A)=\frac{g(D,A)}{H(D)}$

?C4.5 算法是一種決策樹生成算法，它使用信息增益比（gain ratio）來選擇最優分裂屬性，具體步驟如下：
1、計算所有樣本的類別熵（H）。
2、對于每一個屬性，計算該屬性的熵【也為自身熵】（Hi）。
3、對于每一個屬性，計算該屬性對于分類所能夠帶來的信息增益（Gi = H - Hi）。
4、計算每個屬性的信息增益比（gain ratio = Gi / Hi），即信息增益與類別自身熵的比值。
選擇具有最大信息增益比的屬性作為分裂屬性。

?2.2.案例分析

在前面我們算出信息增益：

?第一遍計算:【找首要節點】

天氣的信息增益為: 0.247，

天氣的自身熵值:
$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad-\frac{5}{14}log_{2}\frac{5}{14}-\frac{4}{14}log_{2}\frac{4}{14}-\frac{5}{14}log_{2}\frac{5}{14}=1.577$

5 天晴天、4 天多云、5 天有雨。
信息增益率:? $0.247/1.577 = 0.1566$

2. 溫度的自身熵值:

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad-\frac{4}{14}log_{2}\frac{4}{14}-\frac{6}{14}log_{2}\frac{6}{14}-\frac{4}{14}log_{2}\frac{4}{14}=1.557$

信息增益率:? $0.029/1.557 = 0.0186$

3. 濕度的自身熵值:

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad-\frac{7}{14}log_{2}\frac{7}{14}-\frac{7}{14}log_{2}\frac{7}{14}=1.0$

信息增益率:? $0.151/1.0 = 0.151$

4. 有風的自身熵值:

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad-\frac{8}{14}log_{2}\frac{8}{14}-\frac{6}{14}log_{2}\frac{6}{14}=0.985$

信息增益率:? $0.048/0.985 = 0.049$

?信息增益率排序：天氣（0.1566）濕度（0.151）有風（0.049）溫度（0.0186）天氣 > 濕度 > 有風 > 溫度，然后后面以此類推

?3.CART決策樹

3.1基尼值和基尼指數

????????CART 是Classification and Regression Tree的簡稱，這是?種著名的決策樹學習算法,分類和回歸任務都可?。

????????基尼值Gini（D）：從數據集D中隨機抽取兩個樣本，其類別標記不?致的概率。故，Gini（D）值越?，數據集D的純 度越?。

數據集 D 的純度可?基尼值來度量:

????????基尼指數Gini_index（D）：?般，選擇使劃分后基尼系數最?的屬性作為最優化分屬性。

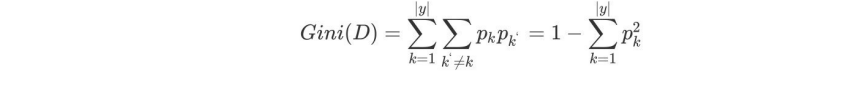
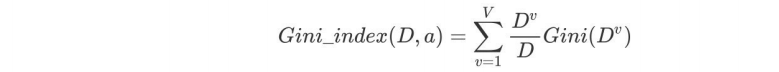
?一看概念介紹就懵，我們自己上案例

3.2案例分析

現有一張貸款申請表如下：

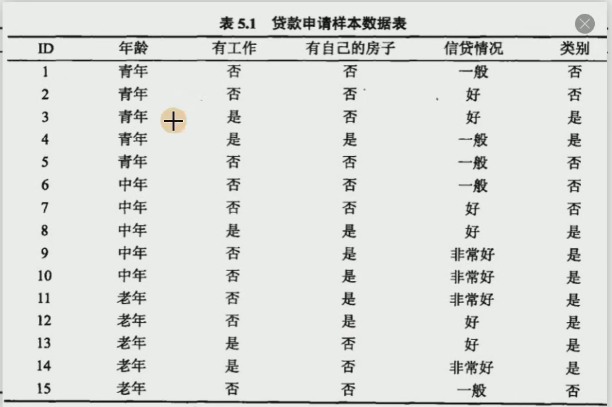
青年（5 人，2 人貸款）的基尼系數：

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\frac{2}{5}*(1-\frac{2}{5})+\frac{3}{5}*(1-\frac{3}{5})=0.48$

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad2*\frac{2}{5}*(1-\frac{2}{5})=0.48$

如果是類別是二分類，則基尼系數：

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad p(1-p)+(1-p)p=2p(1-p)$

非青年（10 人，7 人貸款）的基尼系數：

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad2*\frac{7}{10}*(1-\frac{7}{10})=0.42$

總公式：

$\quad\quad\quad\quad\quad\quad\quad\frac{5}{15}*[2*\frac{2}{5}*(1-\frac{2}{5})]+\frac{10}{15}*[2*\frac{7}{10}*(1-\frac{7}{10})]=0.44$

在 $A1=2$ （中年）條件下，D 的基尼指數：

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\frac{5}{15}*[2*\frac{3}{5}*(1-\frac{3}{5})]+\frac{10}{15}*[2*\frac{6}{10}*(1-\frac{6}{10})]=0.48$

在 $A1=3$ 條件下，D 的基尼：

$\quad\quad\quad\quad\quad\quad\quad\frac{5}{15}*[2*\frac{4}{5}*(1-\frac{4}{5})]+\frac{10}{15}*[2*\frac{5}{10}*(1-\frac{5}{10})]=0.44$

?由于 $\text{Gini}(D,A_1=1$ 和 $\text{Gini}(D,A_1=3)$ 相等，都可以選作 $A_1$ 的最優切分點?

?求特征 $A_2$ 和 $A_3$ 的基尼指數：

$\quad\quad\quad\quad\quad\text{Gini}(D,A_2=1)=0.32$

$\quad\quad\quad\quad\quad\quad\text{Gini}(D,A_3=1)=0.27$

由于 $A_2$ 和 $A_3$ 只有一個切分點，所以它們就是最優切分點。
求特征 $A_4$ 的基尼指數：

$\quad\quad\quad\quad\quad\quad\text{Gini}(D,A_4=1)=0.36$

$\quad\quad\quad\quad\quad\quad\quad\quad\text{Gini}(D,A_4=2)=0.47$
$\quad\quad\quad\quad\quad\quad\quad\quad\text{Gini}(D,A_4=3)=0.32$

$\text{Gini}(D,A_4=3)$ 最小，所以 $\text{Gini}(D,A_4=3)$ 為 $A_4$ 的最優切分點。

?????????在 $A_1,A_2,A_3,A_4$ 幾個特征中， $\text{Gini}(D,A_3=1)=0.27$ 最小，所以選擇特征 $A_3$ 為最優特征， $A_3=1$ 為其最優切分點。于是根結點生成兩個子結點，一個是葉結點。對另一個結點繼續使用以上方法在 $A_1,A_2,A_4$ 中選擇最優特征及其最優切分點，結果是 $A_2=1$ 。依此計算得知，所得結點都是葉結點。

三、決策樹剪枝

為什么要剪枝？
????????防止過擬合。
如何剪枝？
????????預剪枝和后剪枝。
預剪枝策略：

1. 限制樹的深度；
2. 限制葉子節點的個數以及葉子節點的樣本數；
3. 基尼系數：

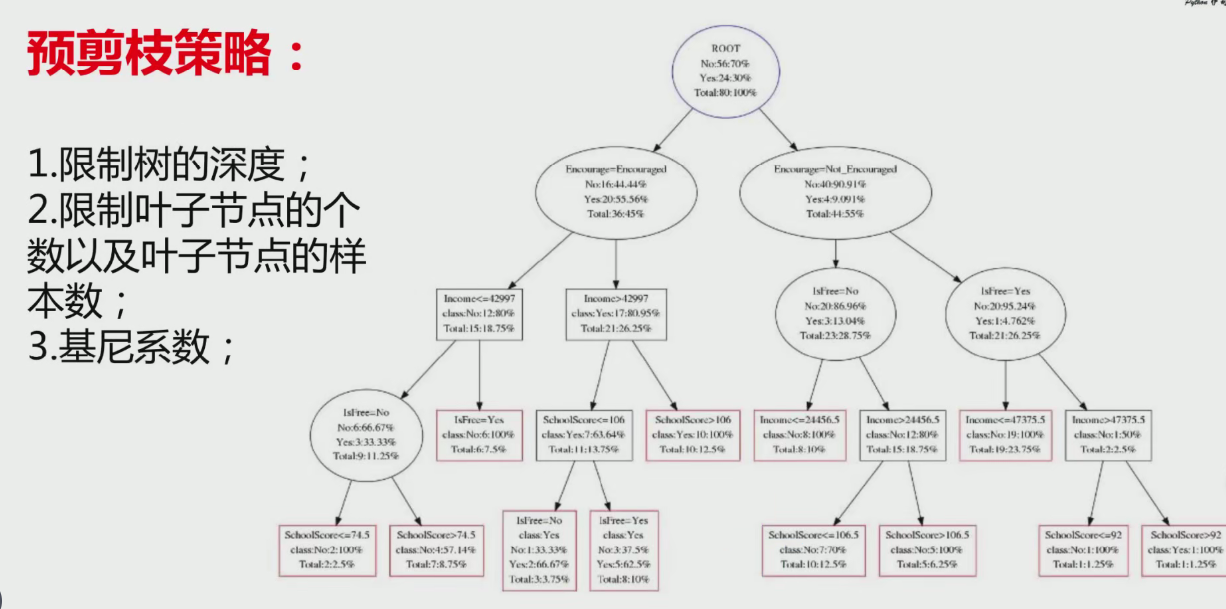
?????????總體來說就是不想讓我們的決策樹變得更深更大，也就是類似與使得xn中n變小。因為在訓練中，如果每一中特征都是生成一個路徑，那重新拿來測試集精確率非常低導致過擬合。

四、決策樹API

class sklearn.tree.DecisionTreeClassifier(criterion='gini', 
splitter='best', max_depth=None, min_samples_split=2, 
min_samples_leaf=1, min_weight_fraction_leaf=0.0, 
max_features=None, random_state=None, max_leaf_nodes=None,min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)

1.criterion: gini or entropy【采用基尼系數還是熵值衡量，默認基尼系數】
2.splitter: best or random 前者是在所有特征中找最好的切分點后者是在部分特征中（數據量大的時候）【默認 best，無需更改】
3.max_features:（表示尋找最優分裂時需要考慮的特征數量，默認為 None，表示考慮所有特征。），log2，sqrt，N 特征小于 50 的時候一般使用所有的【默認取所有特征，無需更改】
4.max_depth: 表示樹的最大深度，數據少或者特征少的時候可以不管這個值，如果模型樣本量多，特征也多的情況下，可以嘗試限制下。如果沒有設置，那么將會把節點完全展開，直到所有的葉子節點都是純的，或者達到最小葉子節點的個數閾值設置。
5.min_samples_split?: （表示分裂一個內部節點需要的最小樣本數，默認為 2），如果某節點的樣本數少于min_samples_split，則不會繼續再嘗試選擇最優特征來進行劃分，如果樣本量不大，不需要管這個值。如果樣本量數量級非常大，則推薦增大這個值。【控制內部節點分裂的情況：假設 < 10，那么分裂的數量小于 10 就不會再次分裂了，默認 2 個】
6.min_samples_leaf?: （葉子節點最少樣本數），這個值限制了葉子節點最少的樣本數，如果某葉子節點數目小于樣本數，則會和兄弟節點一起被剪枝，如果樣本量不大，不需要管這個值【先構成決策樹，再剪枝，當小于某個設定值后，則除此節點以及此節點的分支節點】

?五、電信客戶流失

庫導入部分

import pandas as pd                  # 數據處理庫，用于讀取和操作數據
import numpy as np                   # 數值計算庫，用于數組和矩陣操作
from sklearn.model_selection import train_test_split  # 數據集拆分工具
from sklearn.tree import DecisionTreeClassifier        # 決策樹分類器
from sklearn import metrics          # 模型評估指標庫
from sklearn.model_selection import cross_val_score   # 交叉驗證工具
from imblearn.over_sampling import SMOTE  # 處理類別不平衡的SMOTE算法

數據加載與預處理

# 讀取Excel數據
data = pd.read_excel('電信客戶流失數據.xlsx')# 提取特征和目標變量
x = data.iloc[:, 1:-1]  # 特征數據：取第2列到倒數第2列（排除第一列ID和最后一列標簽）
y = data.iloc[:, -1]    # 目標變量：最后一列（客戶是否流失的標簽）

數據集拆分

# 第一次拆分：將原始數據分為訓練集(80%)和測試集(20%)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42
)

處理類別不平衡問題

# 使用SMOTE算法對訓練集進行過采樣
oversampler = SMOTE(random_state=0)
os_x_train, os_y_train = oversampler.fit_resample(x_train, y_train)# 第二次拆分：將過采樣后的訓練集再分為7:3的訓練子集和驗證子集
os_x_train_w, os_x_test_w, os_y_train_w, os_y_test_w = train_test_split(os_x_train, os_y_train, test_size=0.3, random_state=0
)

客戶流失數據通常存在類別不平衡（流失客戶占比低），SMOTE 通過生成少數類樣本解決此問題
二次拆分是為了用驗證集進行超參數調優，避免直接使用測試集導致的過擬合

超參數網格搜索（核心部分）

# 定義參數搜索范圍
max_depth_param_range = range(2, 25, 2)          # 樹的最大深度：2到24，步長2
min_samples_leaf_param_range = range(2, 25, 2)   # 葉子節點最小樣本數
min_samples_split_param_range = range(2, 25, 2)  # 內部節點分裂最小樣本數
max_leaf_param_range = range(2, 25, 2)           # 最大葉子節點數# 存儲參數組合和對應的分數
scores = []
params_list = []# 四重重循環遍歷所有參數組合（網格搜索）
for i in max_depth_param_range:for j in min_samples_leaf_param_range:for k in min_samples_split_param_range:for n in max_leaf_param_range:params = (i, j, k, n)params_list.append(params)# 創建決策樹模型dtr = DecisionTreeClassifier(criterion='gini',          # 使用基尼系數作為分裂標準max_depth=i,               # 樹的最大深度min_samples_leaf=j,        # 葉子節點最小樣本數min_samples_split=k,       # 內部節點分裂最小樣本數max_leaf_nodes=n,          # 最大葉子節點數random_state=42)# 5折交叉驗證計算召回率（recall）score = cross_val_score(dtr, os_x_train_w, os_y_train_w, cv=5, scoring="recall")score_mean = score.mean()  # 取5折的平均召回率scores.append(score_mean)# 找到找最佳參數組合（召回率最高的參數）
best_index = np.argmax(scores)
best_i, best_j, best_k, best_n = params_list[best_index]

這里采用了四重循環進行網格搜索，計算量較大（12×12×12×12=20736 種組合）
選擇召回率（recall）作為評價指標，適合流失預測場景（更關注盡可能捕捉所有流失客戶）
5 折交叉驗證可以更穩定地評估模型性能，避免單次拆分的隨機性影響

最佳模型訓練與評估

# 輸出最佳參數
print(f"max_depth: {best_i}")
print(f"min_samples_leaf: {best_j}")
print(f"min_samples_split: {best_k}")
print(f"max_leaf_nodes: {best_n}")# 使用最佳參數創建建模型并在原始訓練集上訓練
dtr = DecisionTreeClassifier(criterion='gini',max_depth=best_i,min_samples_leaf=best_j,min_samples_split=best_k,max_leaf_nodes=best_n,random_state=42
)
dtr.fit(x_train, y_train)  # 注意這里用了原始訓練集，而非過采樣的訓練集# 用測試集進行預測
test_predicted = dtr.predict(x_test)# 評估模型性能
score = dtr.score(x_train, y_train)  # 訓練集準確率
print(score)
# 輸出詳細分類報告（包含精確率、召回率、F1分數等）
print(metrics.classification_report(y_test, test_predicted))

?六、回歸樹

??何為回歸樹？

?????????解決回歸問題的決策樹模型即為回歸樹。
特點：
????????必須是二叉樹

(1) 計算最優切分點

因為只有一個變量，所以切分變量必然是 x，可以考慮如下 9 個切分點：

$[1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5]$

【原因：實際上考慮兩個變量間任意一個位置為切分點均可】一個一個切分點計算
<1> 切分點 1.5 的計算?

第一部分:(1,5.56)
第二部分:(2,5.7)、(3,5.91)、（4,6.4)...(10,9.05)

(2) 計算損失

$\quad\quad\quad L(j,s)=\sum_{x_i\in R_1(j,s)}(y_i-\hat{c}_1)^2+\sum_{x_i\in R_2(j,s)}(y_i-\hat{c}_2)^2$

$C_1=5.56$

$\) $C_2=\frac{1}{9}(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5$ $Loss=(5.56-5.56)^2+(5.7-7.5)^2+(5.91-7.5)^2+...+(9.05-7.5)^2$ $\quad\quad=0+15.72$ \(\quad\quad=15.72$ ?

(3) 同理計算其他分割點的損失

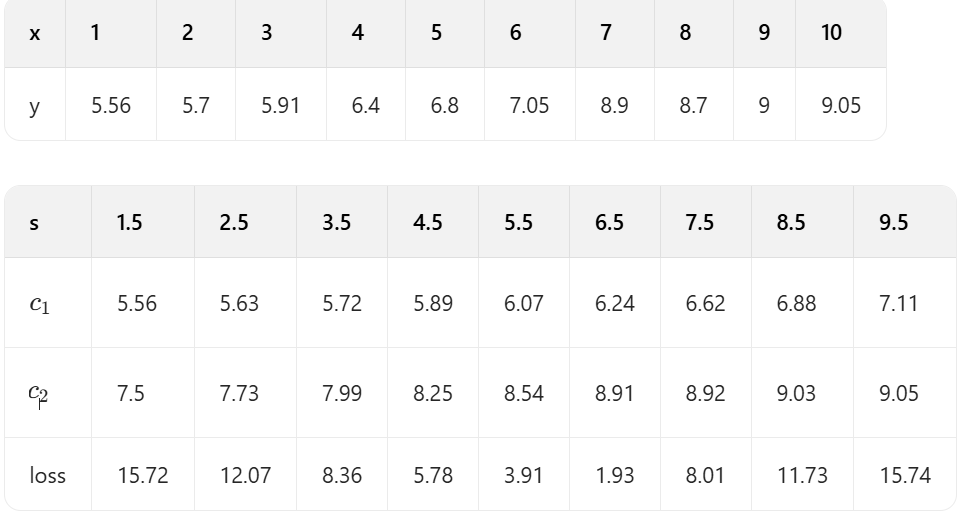
容易看出，當 $s=6.5$ 時，loss=1.93最小，所以第一個劃分點s=6.5。?

(4) 對于小于 6.5 部分

<1> 切分點 1.5 的計算
當s=1.5時，將數據分為兩個部分：
第一部分:(1,5.56)
第二部分:(2,5.7)\)、(3,5.91)、(4,6.4)、(5,6.8)、(6,7.05)

$C_1=5.56$
$C_2=\frac{1}{5}(5.7+5.91+6.4+6.8+7.05)=6.37$
$Loss=0+(5.7-6.37)^2+(5.91-6.37)^2+...+(7.05-6.37)^2\) \(\quad\quad=0+1.3087=1.3087$

?(5) 因此得到:

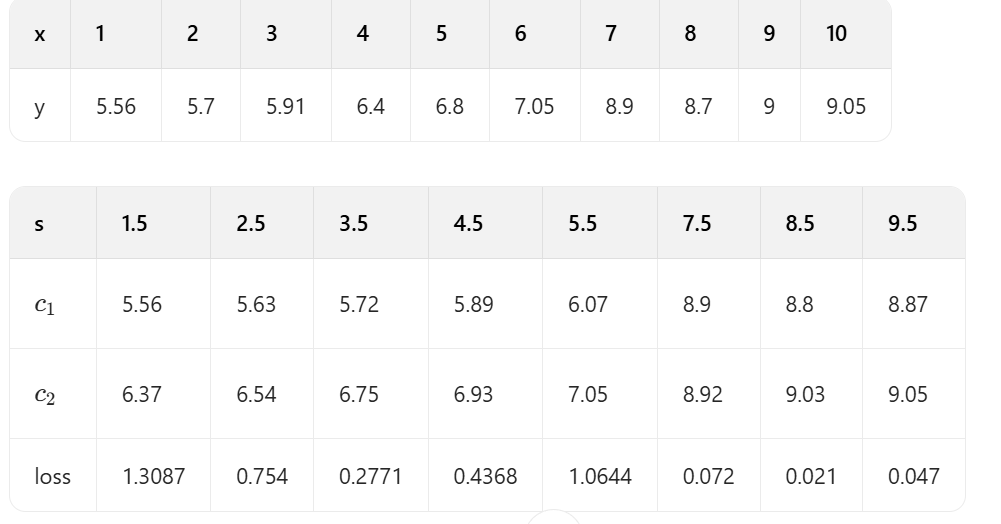
容易看出:

????????<1> 當s=3.5時，loss=0.2771最小，所以第一個劃分點s=3.5。
????????<2> 當s=8.5時，loss=0.021最小，所以第一個劃分點s=8.5。?

(6) 假設只分裂我們計算的這幾次:

那么分段函數為:
????????<1> 當 $x\leq3.5$ ?時， $\frac{1}{3}(5.56+5.7+5.91)=5.72$
????????<2> 當 $3.5<x\leq6.5$ ?時，? $\frac{1}{3}(6.4+6.8+7.05)=6.75$
????????<3> 當 $6.5<x\leq8.5$ ?時，?? $\frac{1}{2}(8.9+8.7)=8.8$
????????<4> 當 $8.5<x$ 時，? ? ? $\frac{1}{2}(9+9.05)=9.025$

(7) 對于預測來說:
特征 x 必然位于其中某個區間內，所以，即可得到回歸的結果，比如說:

如果 x=11, 那么對應的回歸值為 9.025.

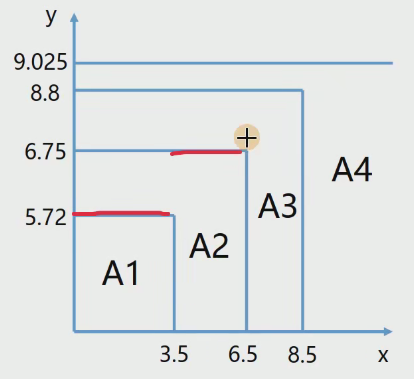
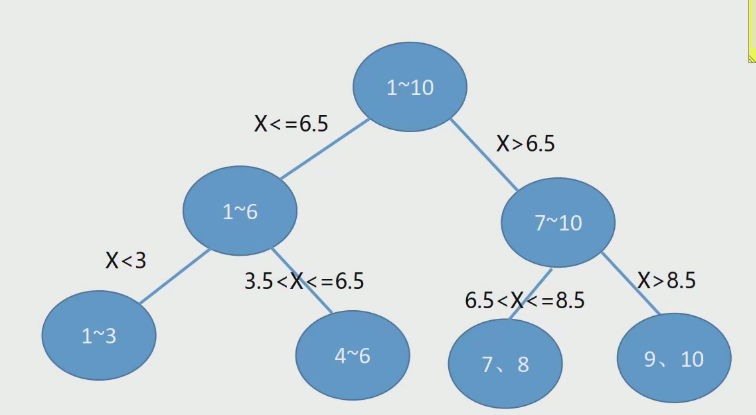
(8) 決策樹構建

七.?回歸樹API

class sklearn.tree.DecisionTreeRegressor(criterion='mse', 
splitter='best', max_depth=None, min_samples_split=2, 
min_samples_leaf=1, min_weight_fraction_leaf=0.0, 
max_features=None, random_state=None, max_leaf_nodes=None, 
min_impurity_decrease=0.0, min_impurity_split=None, presort=False)[source]

criterion：節點分裂依據。默認：mse
- 可選擇：mae(平均絕對誤差) -> 使用絕對值$\sum|y_i - c_1| + \sum|y_i - c_2|$
- 【按默認選擇mse即可】
splitter：默認best，表示以最優的方式切分節點。決定了樹構建過程中的節點分裂策略。值為best，意味著在每個節點上，算法會找出最好的分割點來盡量降低信息熵或者減少均方誤差。如果設置為random，則算法會隨機選擇一個特征進行分裂。
- 【按默認選擇best即可】
max_depth：樹的最大深度。過深的樹可能導致過擬合。
- 【通過交叉驗證來進行選擇】
min_samples_split：默認值是 2. 分裂一個內部節點需要的最小樣本數，
- 【含義與分類相同】
min_samples_leaf：默認值是 1，葉子節點最少樣本數
- 【含義與分類相同】
max_leaf_nodes：設置最多的葉子節點個數，達到要求就停止分裂【控制過擬合】
- 【設置此參數之后max_depth失效】★重要

????????回歸樹的代碼部分比較簡單，重點理解一下它的邏輯過程就行，知道是這樣計算的，不需要實際硬背。

代碼部分

reg = tree.DecisionTreeRegressor()
reg = reg.fit(x,y)