GenAttack：利用無梯度優化的實用黑盒攻擊

Moustafa Alzantot
UCLA
Los Angeles, U.S.A
malzantot@ucla.edu
Yash Sharma
Cooper Union
New York, U.S.A
sharma2@cooper.edu
Supriyo Chakraborty
IBM Research
New York, U.S.A
supriyo@us.ibm.com
Huan Zhang
UCLA
Los Angeles, U.S.A
huanzhang@ucla.edu
Cho-Jui Hsieh
UCLA
Los Angeles, U.S.A
chohsieh@cs.ucla.edu
Mani B. Srivastava
UCLA
Los Angeles, U.S.A
mbs@ucla.edu

摘要

深度神經網絡容易受到對抗樣本的攻擊，即使在黑盒設置下（攻擊者僅被限制為查詢訪問）也是如此。現有的生成對抗樣本的黑盒方法通常需要大量查詢，無論是用于訓練替代網絡還是執行梯度估計。我們提出了 GenAttack，一種利用遺傳算法在黑盒設置下合成對抗樣本的無梯度優化技術。我們在不同數據集（MNIST、CIFAR-10 和 ImageNet）上的實驗表明，GenAttack 能夠成功生成視覺上難以察覺的對抗樣本，以攻擊最先進的圖像識別模型，且所需查詢量比先前方法少幾個數量級。針對 MNIST 和 CIFAR-10 模型，GenAttack 所需的查詢量分別比先前最先進的黑盒攻擊方法 ZOO 減少了約 2126 倍 和 2568 倍。為了將攻擊擴展到大規模高維的 ImageNet 模型，我們進行了一系列優化，進一步提高了攻擊的查詢效率，使得針對 Inception-v3 模型的查詢量比 ZOO 少了 237 倍。此外，我們還展示了 GenAttack 能夠成功攻擊一些最先進的 ImageNet 防御機制，包括集成對抗訓練（ensemble adversarial training）和不可微分或隨機化的輸入變換（randomized input transformations）。我們的結果表明，進化算法為研究有效的黑盒攻擊開辟了一個充滿前景的領域。

對抗樣本、深度學習、遺傳算法、計算機視覺

1. 引言

深度神經網絡（DNNs）在機器學習和人工智能的各個任務中已取得最先進的性能。盡管其效果顯著，但最近的研究揭示了 DNNs 對對抗樣本的脆弱性[11, 29]。例如，對圖像施加一個幾乎無法察覺的擾動，就能導致訓練良好的 DNN 錯誤分類。有目標的對抗樣本甚至能導致模型錯誤分類到攻擊者選定的類別。此外，研究人員已經證明這些對抗樣本在物理世界[4, 16]中仍然有效，并且可以在不同的數據模態中生成，例如自然語言[2]和語音[1]領域。DNNs 在對抗樣本面前表現出的魯棒性不足，對安全關鍵應用引發了嚴重擔憂。

幾乎所有先前關于對抗攻擊的工作[7, 8, 11, 12, 16, 21]都使用基于梯度的優化來尋找成功的對抗樣本。然而，梯度計算只能在攻擊者完全了解模型架構和權重的情況下進行。因此，這些方法僅適用于白盒(white-box) 設置，即攻擊者擁有對目標 DNN 的完全訪問和控制權。然而，在攻擊現實世界系統時，需要考慮在黑盒(black-box) 設置下執行對抗攻擊的問題，即不透露任何關于網絡架構、參數或訓練數據的信息。在這種情況下，攻擊者只能訪問分類器的輸入-輸出對。在這種設置下，一種流行的方法是攻擊訓練好的替代網絡（substitute networks），并希望生成的樣本能遷移（transfer）到目標模型[22]。這種方法受到替代模型與目標模型之間固有的模型失配（model mismatch）以及訓練替代網絡所需的高計算成本的困擾。最近的工作使用基于坐標的有限差分法（coordinate-based finite difference methods）直接從置信度分數估計梯度[9]，但這些攻擊在計算上仍然非常昂貴，需要依賴優化技巧才能保持可行性。這兩種方法都是查詢密集型的，從而限制了它們在現實場景中的實用性。

基于上述動機，我們提出了 GenAttack，一種無需計算甚至無需近似梯度即可生成對抗樣本的新方法，使得在黑盒情況下進行高效對抗攻擊成為可能。為了執行無梯度優化（gradient-free optimization），我們采用了一種基于種群的遺傳算法方法，迭代地進化一組可行解直至成功。我們還提出了一些技巧，使得 GenAttack 在攻擊基于大規模高維數據集（如ImageNet[10]）訓練的模型時，仍能保持其查詢效率。

由于其無梯度的特性，GenAttack 對執行梯度掩碼（gradient masking）或混淆（obfuscation）的防御具有魯棒性[3]。因此，與許多當前的黑盒攻擊方法不同，GenAttack 可以在黑盒設置中高效地構建擾動，以繞過一些最近提出的操縱梯度的防御方法。

我們使用最先進的圖像分類模型評估了 GenAttack，發現該算法能夠以比當前方法少得多的查詢量成功執行 有目標(targeted) 的黑盒攻擊。在我們的 MNIST、CIFAR-10 和 ImageNet 實驗中，GenAttack 所需的查詢量分別比當前最先進的黑盒攻擊方法少約 2126 倍、2568 倍 和 237 倍。此外，我們還展示了 GenAttack 對最先進 ImageNet 防御機制的成功攻擊，例如集成對抗訓練[30]以及隨機化、不可微分的輸入變換防御[13]。這些結果說明了 GenAttack 查詢效率高和無梯度特性的強大之處。

總而言之，我們的貢獻如下：

• 我們提出了 GenAttack，一種利用基于種群的優化（population-based optimization）生成對抗樣本的新型無梯度方法。我們的實現已開源1，以促進對抗魯棒性研究的進一步發展。
  (腳注1: https://github.com/nesl/adversarial_genattack)
• 我們證明，在受限的黑盒設置下，結合遺傳優化、降維和自適應參數縮放的 GenAttack，能夠生成對抗樣本，迫使在 MNIST、CIFAR-10 和 ImageNet 上訓練的最先進圖像分類模型將樣本錯誤分類到選定的目標標簽，且所需的查詢量顯著少于先前的方法。
• 我們通過展示 GenAttack 對幾種最先進 ImageNet 防御機制（即集成對抗訓練和隨機化、不可微分的輸入變換）的成功攻擊，進一步強調了其有效性。 據我們所知，我們是第一個展示成功對抗這些防御的黑盒攻擊的工作。

本文其余部分組織如下：第 2 節總結了相關工作。第 3 節正式定義了我們攻擊的威脅模型。第 4 節討論 GenAttack 的細節。第 5 節描述了我們的評估實驗及其結果。最后，第 6 節總結了論文，并討論了進化算法在生成對抗樣本方面的效用。

2. 相關工作

在下文中，我們總結了最近在生成對抗樣本（包括白盒和黑盒情況）以及防御對抗樣本方面的方法。更多細節請參閱所引用的工作。

2.1 白盒攻擊與可遷移性（Transferability）

在 白盒（white-box） 情況下，攻擊者完全了解并擁有對目標 DNN 的完全訪問權限。在這種情況下，攻擊者能夠使用反向傳播進行梯度計算，從而實現高效的基于梯度的攻擊。我們簡要總結以下幾種重要的白盒攻擊公式。

• L-BFGS。[29] 使用帶盒約束（box-constrained）的 L-BFGS 來最小化添加的對抗噪聲的 ${?}_2$ 范數 $||\delta |{|}_2$，約束條件為$f(x+\delta )=l$（預測為類別 $l$) 和 $x+\delta \in [0,1{]}^m$（輸入在有效像素范圍內）。
  其中 f:Rm→{1,...,k}f:\mathbb{R}^{m}\rightarrow\{1,...,k\}f:Rm→{1,...,k} 是分類器，將數據樣本映射到離散標簽，l∈{1,...,k}l\in\{1,...,k\}l∈{1,...,k} 是目標輸出標簽，$\delta$ 是添加的噪聲。

• FGSM & I-FGSM。[11] 提出了快速梯度符號方法（FGSM）來快速生成對抗樣本。在 $L_{\infty }$ 失真約束 $\Vert \delta {\Vert }_{\infty }\le ?$ 下，FGSM 使用訓練損失 $J$ 相對于原始輸入 ${\mathbf{x}}_0$ 和真實標簽$l$ 的梯度的符號來生成對抗樣本：$\mathbf{x}={\mathbf{x}}_0+??\text{sign}(?J({\mathbf{x}}_0,l))$。
  類似地，可以通過計算相對于指定目標類別 $t$ 的損失，并沿負梯度方向移動來實現有目標攻擊。
  在[16]中，提出了 FGSM 的迭代版本（I-FGSM），其中 FGSM 在更精細的失真約束下迭代使用，然后進行 $?$-球裁剪（$?$-ball clipping）。在[20]中，引入了投影梯度下降（PGD），對 I-FGSM 進行修改以包含隨機起點（random starts）。

• C&W & EAD。與利用訓練損失不同，C&W[7] 設計了一個基于 DNN 中 logit 層表示的 $L_2$ 正則化損失函數來制作對抗樣本。通過變量變換處理盒約束 $\mathbf{x}\in [0,1{]}^p$，他們使用 Adam[15] 來最小化 $??f(\mathbf{x},t)+||\mathbf{x}?{\mathbf{x}}_0|{|}_2^2$。
  其中 $f(x,t)$ 是一個依賴于 logit 層值和目標類別 $t$ 的損失函數。EAD[8] 通過最小化額外的 $L_1$懲罰項推廣了該攻擊，并已被證明能生成更魯棒和可遷移的對抗樣本[19, 24, 25]。

白盒攻擊也可以通過利用可遷移性（transferability）[18] 在黑盒設置中使用。可遷移性指的是使用一個模型生成的對抗樣本通常會被另一個模型錯誤分類的特性[27]。替代模型方法進行黑盒攻擊就是利用這一特性來生成成功的對抗樣本，我們將在下一小節中討論。

2.2 黑盒攻擊

在文獻中， 黑盒（black-box） 攻擊設置指的是攻擊者可以自由訪問目標 DNN 的輸入和輸出，但無法在網絡上執行反向傳播的情況。提出的方法依賴于可遷移性和梯度估計，總結如下。

• 替代網絡（Substitute Networks）。早期的黑盒攻擊方法利用自由查詢的能力來訓練一個替代模型（substitute model），作為目標 DNN 的代表[22]。然后可以使用任何白盒技術攻擊該替代 DNN，并將生成的對抗樣本用于攻擊目標 DNN。由于替代模型被訓練成在分類規則上代表目標 DNN，因此替代模型的對抗樣本預期與相應目標 DNN 的對抗樣本相似。然而，這種方法依賴于可遷移性屬性，而不是直接攻擊目標 DNN，這并不完美，從而限制了攻擊者的強度。此外，訓練替代模型在計算上非常昂貴，在攻擊大型模型（如 Inception-v3[28]）時幾乎不可行。

• 零階優化（Zeroth Order Optimization, ZOO）。零階優化（ZOO）攻擊建立在 C&W 攻擊的基礎上執行黑盒攻擊[9]，通過修改損失函數使其僅依賴于 DNN 的輸出，并使用通過有限差分獲得的梯度估計進行優化。然而，ZOO 需要巨大的查詢量，因為每個坐標的梯度估計需要 $2$ 次查詢。因此，在 ImageNet 數據集上攻擊 Inception-v3[28] 需要 $299\times 299\times 3\times 2=536,406$ 次查詢（每個優化步驟）。為了解決這個問題，使用了隨機坐標下降（SCD），每個步驟只需要 $2$ 次查詢。盡管如此，當坐標數量很大時，SCD 的收斂可能很慢，因此降低擾動的維度和使用重要性采樣也至關重要。應用這些技術后，與替代模型方法不同，攻擊 Inception-v3 在計算上變得可行。然而，正如我們在實驗中所展示的，梯度估計過程仍然相當查詢低效，因此對于攻擊現實世界系統來說不切實際。

在并行的工作中，[6, 14, 31] 也研究了黑盒對抗攻擊的效率和強度問題，但我們的工作在目標和方法上仍然是獨特的。[6] 側重于攻擊僅能部分訪問查詢結果的黑盒模型。值得注意的是，他們的方法在攻擊未防御的 ImageNet 模型時，平均需要的查詢量大約是我們的 72 倍。[14] 和 [31] 研究了與我們考慮的相同威脅模型下黑盒攻擊的效率，然而，兩者都依賴于梯度估計（gradient estimation），而不是無梯度優化（gradient-free optimization）。[14] 估計參數化搜索分布下損失期望值的梯度，這可以看作是在隨機高斯基上的有限差分估計。[31] 則摒棄了 ZOO 的逐坐標估計，采用了縮放的隨機全梯度估計器（scaled random full gradient estimator）。盡管我們將這兩項工作視為并行工作，但為了完整性，我們在結果中提供了我們的“無梯度”方法與其他查詢高效的“梯度估計”方法之間的比較。

2.3 防御對抗攻擊

• 對抗訓練（Adversarial Training）。對抗訓練通常通過使用標簽修正后的對抗樣本增強原始訓練數據集來重新訓練網絡來實現。在[20]中，一個高容量網絡被訓練來對抗 $L_{\infty }$ 約束的 PGD（帶隨機起點的 I-FGSM），在 $L_{\infty }$ 球內獲得了強大的魯棒性，但已被證明對基于其他魯棒性指標優化的攻擊魯棒性較低[23, 24, 32]。在[30]中，訓練數據通過從其他模型遷移過來的擾動進行增強，并被證明對遷移的對抗樣本具有強大的魯棒性。我們在實驗結果中證明，它對查詢高效的黑盒攻擊（如 GenAttack）的魯棒性較低。

• 梯度混淆（Gradient Obfuscation）。已經發現，許多最近提出的防御通過操縱梯度（使其不存在或不正確、依賴于測試時的隨機性，或根本無法使用）來提供對強對抗攻擊的表觀魯棒性。具體來說，在分析 ICLR 2018 聲稱具有白盒魯棒性的未認證防御時，發現 9 個中有 7 個依賴于這種現象[3]。研究還表明，基于 FGSM 的對抗訓練通過使梯度指向錯誤的方向來學習成功[30]。

一種依賴梯度混淆的防御是利用不可微分的輸入變換（non-differentiable input transformations），例如位深度縮減（bit-depth reduction）、JPEG 壓縮和總方差最小化（total variance minimization）[13]。在**白盒（white-box）情況下，這種防御可以通過在反向傳播過程中用恒等函數替換不可微分的變換，成功地被基于梯度的技術攻擊[3]。雖然有效，但這種方法不適用于黑盒（black-box）情況，因為攻擊者需要了解不可微分組件的信息。我們在實驗結果中證明，GenAttack 由于是無梯度的，因此不受所述梯度操縱的影響，可以自然地在黑盒（black-box）**情況下處理此類過程。請注意，許多需要梯度估計的黑盒攻擊（包括[9, 14, 31]）在存在不可微分輸入變換時無法直接應用。

3. 威脅模型

我們考慮以下攻擊場景。攻擊者不了解網絡架構、參數或訓練數據。攻擊者只能將目標模型作為黑盒函數進行查詢：

$$f:{\mathbb{R}}^d\to [0,1{]}^K$$

其中 $d$ 是輸入特征的數量，$K$ 是類別數量。函數 $f$ 的輸出是模型預測分數的集合。請注意，攻擊者無法訪問在網絡隱藏層（包括 logits）中計算的中間值。

攻擊者的目標是執行 有目標（targeted） 攻擊。正式地說，給定一個被模型正確分類的良性輸入樣本 $\mathbf{x}$，攻擊者試圖找到一個擾動樣本${\mathbf{x}}_{adv}$，使得網絡將產生攻擊者從標簽集 {1..K}\{1..K\}{1..K} 中選擇的期望目標預測$t$。此外，攻擊者還試圖最小化 $L_p$距離，以保持 ${\mathbf{x}}_{orig}$ 和${\mathbf{x}}_{adv}$ 之間的感知相似性。即：

arg?max?c∈{1..K}f(xadv)c=t滿足?∣∣x?xadv∣∣p≤δ\operatorname*{arg\,max}_{c\in\{1..K\}}f(\mathbf{x}_{adv})_{c}=t\quad\text{滿足 }||\mathbf{x}-\mathbf{x}_{adv}||_{p}\leq\deltac∈{1..K}argmax?f(xadv?)c?=t滿足?∣∣x?xadv?∣∣p?≤δ

其中距離范數函數 $L_p$ 通常選擇為 $L_2$ 或 $L_{\infty }$。

此威脅模型等同于先前黑盒攻擊工作[9, 22]中的模型，類似于密碼學中的選擇明文攻擊（CPA），即攻擊者向受害者提供任何選定的明文消息并觀察其加密密碼輸出。

4. GenAttack 算法

GenAttack 依賴于遺傳算法（genetic algorithms），這是一種基于種群的無梯度優化策略。遺傳算法受自然選擇過程的啟發，迭代地進化候選解的種群 $\mathcal{P}$ 以趨向更好的解。每次迭代中的種群稱為一代（generation）。在每一代中，使用**適應度（fitness）函數評估種群成員的質量。“適應度更高”的解更有可能被選擇用于繁殖下一代。下一代通過交叉（crossover）和變異（mutation）的組合產生。交叉是取多個父代解并從中產生子代解的過程；它類似于生物繁殖和交叉。變異根據用戶定義的小概率變異概率（mutation probability）**對種群成員施加小的隨機擾動。
這樣做是為了增加種群成員的多樣性，并更好地探索搜索空間。

算法 1 描述了 GenAttack 的操作。算法輸入是原始樣本 ${\mathbf{x}}_{orig}$ 和攻擊者選擇的目標分類標簽 $t$。算法計算一個對抗樣本 ${\mathbf{x}}_{adv}$，使得模型將 ${\mathbf{x}}_{adv}$ 分類為 $t$ 且 $||{\mathbf{x}}_{orig}?{\mathbf{x}}_{adv}|{|}_{\infty }\le {\delta }_{max}$。我們定義種群大小為 $N$，“變異概率” 為$\rho$， “變異范圍” 為 $\alpha$。

GenAttack 通過在原始樣本 ${\mathbf{x}}_{orig}$ 為中心的球體（半徑 $={\delta }_{max}$）上定義的均勻分布中隨機選取樣本來初始化圍繞給定輸入樣本 ${\mathbf{x}}_{orig}$ 的種群。這是通過向輸入向量 ${\mathbf{x}}_{orig}$ 的每個維度添加范圍在（$?{\delta }_{max},{\delta }_{max}$) 內的隨機噪聲來實現的。然后，重復以下步驟直到找到成功的樣本：評估每個種群成員的適應度，選擇父代，執行交叉和變異以形成下一代。

• 適應度函數（Fitness function）：子程序 ComputeFitness 評估每個種群成員的適應度（即質量）。由于適應度函數應反映優化目標，一個合理的選擇是直接使用分配給目標類別標簽的輸出分數。然而，我們發現同時激勵其他類別概率的降低會更有效。我們還發現使用對數（log）有助于避免數值不穩定性問題。因此，我們選擇以下函數：
  $$ComputeFitness(\mathbf{x})=\log f(\mathbf{x}{)}_t?\log \sum _{j=0,j\ne t}^{j=k}f(\mathbf{x}{)}_c$$

• 選擇（Selection）：每次迭代中的種群成員根據其適應度值進行排序。適應度較高的成員更有可能成為下一代的一部分，而適應度較低的成員更有可能被替換。我們通過計算適應度值的 Softmax 將其轉換為概率分布，從而計算每個種群成員的選擇概率。然后，我們根據該分布獨立地在種群成員中隨機選擇父代對。我們還發現應用 精英保留（elitism） 技術[5]很重要，即當前代的 精英（elite） 成員（適應度最高的成員）保證成為下一代的一員。

• 交叉操作（Crossover operation）：選擇后，父代進行交配以產生下一代成員。子代通過根據選擇概率 ((p,1-p)) 從 $paren{t}_1$ 或$paren{t}_2$ 中選擇每個特征值來生成，其中 $p$ 定義為：
  $$p=\frac{fitness(parent\_1)}{fitness(parent\_1)+fitness(parent\_2)}$$

• 變異操作（Mutation operation）：為了促進種群成員之間的多樣性和對搜索空間的探索，在每次迭代結束時，種群成員可以根據概率 $\rho$ 進行變異。將從范圍（$?\alpha {\delta }_{\max },\alpha {\delta }_{\max }$) 均勻采樣的隨機噪聲應用于交叉操作結果的各個特征。最后，執行裁剪算子 ${\Pi }_{{\delta }_{max}}$ 以確保像素值在距離良性樣本${\mathbf{x}}_{orig}$ 允許的 $L_{\infty }$ 距離范圍內。

4.1 提高查詢效率

在本節中，我們介紹了在 GenAttack 算法中采用的幾個優化措施，這些措施顯著提高了查詢效率。

4.1.1 降維（Dimensionality Reduction）

一方面，擴展遺傳算法以高效探索高維搜索空間（如 ImageNet 模型）需要在每一代使用較大的種群規模。另一方面，評估每個成員的適應度意味著以新查詢的形式增加成本。因此，我們將 GenAttack 限制為使用相對較小的（例如，小于 10）種群規模。我們在第 5.3 節中提供了關于種群規模與查詢次數之間權衡的更多討論。

此外，受[31]工作的啟發，我們試圖通過執行搜索空間的降維并在低維空間中定義對抗噪聲來解決擴展遺傳算法（進而擴展 GenAttack）的挑戰。為了計算對抗樣本，我們應用雙線性調整大小（bilinear resizing）（這是
確定性的），將噪聲縮放到與輸入相同的大小。因此，

$${\mathbf{x}}_{orig}\in [0,1{]}^d,e_{adv}\in [0,1{]}^{d^{\prime }},{\mathbf{x}}_{adv}=S(e_{adv})+{\mathbf{x}}_{orig}$$

其中 $e_{adv}$ 是學習到的對抗噪聲，$S$ 是雙線性調整大小操作，$d^{\prime }$ 的選擇使得 $d^{\prime }<d$。實際上，這導致了一個壓縮的對抗噪聲向量，其中 $e_{adv}$ 的一個值用于擾動 ${\mathbf{x}}_{orig}$ 的多個相鄰像素以產生${\mathbf{x}}_{adv}$。我們注意到，這種方法顯著提高了 GenAttack 針對高維模型（如 ImageNet 模型）的查詢效率，同時在 $L_{\infty }$ 約束下保持了攻擊成功率。

4.1.2 自適應參數縮放（Adaptive Parameter Scaling）

為了減輕遺傳算法對超參數值（例如變異率、種群大小、變異范圍）的敏感性，我們使用了一種退火方案（annealing scheme）：如果檢測到搜索算法在連續多次迭代中停滯而沒有進一步改善目標函數，則逐漸減小算法參數（即變異率 $\rho$ 和變異范圍 $\alpha$）。自適應縮放緩解了這種情況：過高的變異率可能允許目標函數值初始快速下降，之后算法可能陷入停滯而無法取得進一步進展。

我們采用指數衰減來更新參數值：

$$\rho =\max ({\rho }_{\min },0.5\times (0.9{)}^{\text{num\_plateaus}})(1)$$
$$\alpha =\max ({\alpha }_{\min },0.4\times (0.9{)}^{\text{num\_plateaus}})(2)$$
其中 ${\rho }_{\min }$ 和 ${\alpha }_{\min }$ 分別選擇為 0.1 和 0.15，num_plateaus 是一個計數器，每當算法連續 100 步未能改善種群精英成員（最高適應度）的適應度時遞增。

5. 結果

我們通過攻擊最先進的 MNIST、CIFAR-10 和 ImageNet 圖像分類模型來評估 GenAttack。對于每個數據集，我們使用與 ZOO 工作[9]中相同的模型。對于 MNIST 和 CIFAR-10，模型準確率分別為 99.5% 和 80%。讀者可以參考[7]了解這些模型架構的更多細節。對于 ImageNet，我們使用 Inception-v3[28]，其 top-5 準確率為 94.4%，top-1 準確率為 78.8%。我們比較了 GenAttack 與 ZOO 在這些模型上的有效性，比較指標包括攻擊成功率（ASR）、運行時間以及成功所需的中位數查詢次數。運行時間和查詢計數統計僅基于成功的攻擊計算。一次查詢意味著對單個輸入圖像評估一次目標模型輸出。使用作者的代碼2，我們根據作者用于生成實驗結果[9]的實現為每個數據集配置 ZOO。我們還評估了最先進的白盒 C&W 攻擊[7]，假設直接訪問模型，以提供攻擊成功率的參考。
(腳注2: https://github.com/huanzhang12/ZOO-Attack)

此外，我們使用作者在以下鏈接3發布的模型評估了 GenAttack 對集成對抗訓練[30]的有效性。集成對抗訓練被認為是針對黑盒攻擊的最先進 ImageNet 防御方法，被證明在托管競賽中能有效提供對遷移攻擊的魯棒性[17, 26, 30]。最后，我們評估了最近提出的隨機化、不可微分的輸入變換防御[13]，以測試 GenAttack 對梯度混淆的性能。我們發現，由于其無梯度的特性，GenAttack 可以原樣處理此類防御。
(腳注3: 原文鏈接缺失，此處保留占位符)

圖 1： GenAttack 生成的 MNIST 對抗樣本。行標簽是真實標簽，列標簽是目標標簽。

圖 2： GenAttack 生成的 CIFAR-10 對抗樣本。行標簽是真實標簽，列標簽是目標標簽。

超參數（Hyperparameters）。 對于我們所有的 MNIST 和 CIFAR-10 實驗，我們將 GenAttack 的最大查詢次數限制為 100,000 次，并將超參數固定為以下值：變異概率 $\rho =5\text{e}?2$(0.05)，種群大小 $N=6$，步長 $\alpha =1.0$。對于我們所有的 ImageNet 實驗，由于圖像尺寸幾乎是 CIFAR-10 的 100 倍，我們使用最大 1,000,000 次查詢，并根據第 4 節前面的討論自適應更新 $\rho$ 和 $\alpha$ 參數。此外，我們實驗了帶降維和不帶降維的情況（$d^{\prime }=96$）。為了匹配 ZOO 成功樣本計算的平均 $L_{\infty }$ 失真，我們分別為 MNIST、CIFAR-10 和 ImageNet 實驗設置 δmax={0.3,0.05,0.05}\delta_{max}=\{0.3,0.05,0.05\}δmax?={0.3,0.05,0.05}。由于遺傳算法有各種調整參數，我們在第 5.3 節進行了參數敏感性研究。

5.1 查詢量比較

我們通過成功所需的查詢次數比較 GenAttack 和 ZOO，并提供 C&W 白盒結果以全面看待攻擊成功率（ASR）。對于 MNIST、CIFAR-10 和 ImageNet，我們分別從測試集中隨機選擇 1000、1000 和 100 個正確分類的圖像。對于每個圖像，我們選擇一個隨機的目標標簽。

5.1.1 MNIST 和 CIFAR-10

表 1 顯示了我們實驗的結果。結果表明，ZOO 和 GenAttack 都可以在 MNIST 和 CIFAR-10 數據集上成功，但 GenAttack 的效率在各自數據集上分別高出 2126 倍 和 2568 倍。隨機選擇的一組 MNIST 和 CIFAR-10 測試圖像及其針對其他標簽生成的對抗樣本分別顯示在圖 1 和圖 2 中。

• ImageNet：表 2 顯示了我們對正常訓練的 (InceptionV3) 和集成對抗訓練的 (Ens4AdvInceptionV3) ImageNet 模型的實驗結果。為了展示降維和自適應參數縮放的效果，我們將沒有這些技巧的 GenAttack 表示為 “GA baseline”。在 ImageNet 上，ZOO 在有目標攻擊中無法持續成功，這很重要，因為它表明 GenAttack 足夠高效，可以有效地擴展到 ImageNet。此外，GenAttack 的查詢效率比 ZOO 高出約 237 倍，比 GA baseline 高出 9 倍。針對 Inception-v3 測試圖像及其相關對抗樣本的一個隨機示例如圖 3所示。

5.1.2 與并行工作的查詢高效攻擊比較

在準備本稿件時，我們注意到一些并行工作也被開發出來以解決查詢高效的對抗攻擊問題。為了完整性，我們也展示了我們的方法與其他貢獻的比較。與執行無梯度優化的 GenAttack 不同，[31] 和 [14] 提出了比 ZOO 更高效的梯度估計程序。表 3 顯示了三種方法結果的比較。我們注意到，雖然這三種方法都比之前最先進的方法（ZOO）查詢效率顯著提高，但在相同的 $L_{\infty }$ 距離約束下，GenAttack 比 [14] 的工作少需要 25% 的查詢，代價是 $L_2$ 距離略有增加，這主要是由于使用了降維。此外，即使 [31] 在 $L_{\infty }$ 和 $L_2$ 失真上都更高，GenAttack 所需的查詢量也比 [31] 少 15%。值得注意的是，[31] 有額外的后處理步驟來減少失真量，但這顯著增加了查詢成本。因此，我們報告了所有攻擊在首次成功時的查詢次數和失真距離。

5.2 攻擊防御機制

在接下來的部分，我們展示 GenAttack 如何成功突破一組旨在提高模型對抗攻擊魯棒性的最先進防御方法。

5.2.1 攻擊集成對抗訓練（Ensemble Adversarial Training）

集成對抗訓練將其他已訓練模型上生成的對抗輸入納入模型的訓練數據中，以提高其對對抗樣本的魯棒性[30]。這已被證明是在 NIPS 2017 競賽期間提供對基于遷移的黑盒攻擊魯棒性的最有效方法。

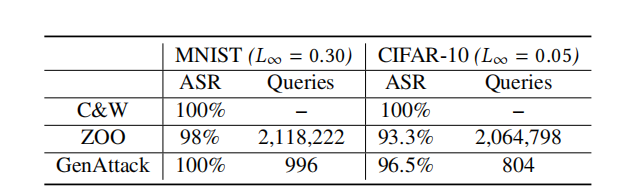
表 1： C&W（白盒）攻擊、ZOO 和 GenAttack 在等效 $L_{\infty }$失真下的攻擊成功率（ASR）和中位數查詢次數。查詢次數的中位數基于成功樣本計算。白盒攻擊不關心查詢次數。

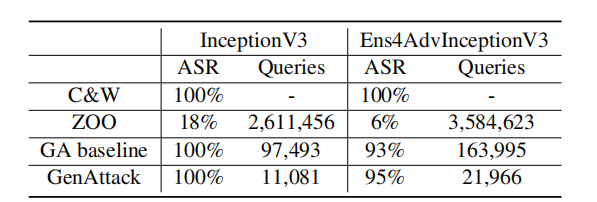
表 2： C&W（白盒）攻擊、ZOO 和 GenAttack 在等效 $L_{\infty }$ 失真 (0.05) 下的攻擊成功率（ASR）和中位數查詢次數。查詢次數的中位數基于成功樣本計算。GA baseline 是不使用降維和自適應參數縮放技巧的 GenAttack。

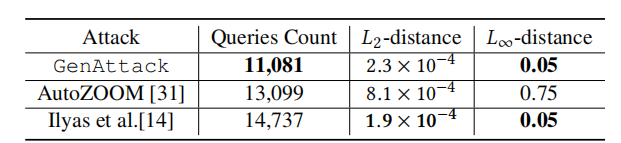
表 3： 與并行工作對抗 ImageNet Inception V3 模型的比較，包括查詢次數的中位數以及原始圖像與對抗圖像之間的每像素 $L_2$ 和 $L_{\infty }$ 距離。

我們證明該防御對查詢高效的黑盒攻擊（如 GenAttack）的魯棒性要低得多。

我們進行了一項實驗來評估 GenAttack 對作者[30]發布的集成對抗訓練模型（即 Ens4AdvInceptionV3）的有效性。我們使用了之前 ImageNet 實驗中相同的 100 個隨機采樣的測試圖像和目標。我們發現 GenAttack 能夠對這個防御強大的模型實現 95% 的成功率，顯著優于 ZOO。如表 2 所示，我們比較了集成對抗訓練模型和原始 Inception-v3 模型之間的成功率和查詢次數的中位數。我們的比較表明，這些積極的結果僅以查詢量有限的增加為代價。我們還注意到，在 NIPS 2017 競賽中用于評估的最大 $L_{\infty }$ 失真范圍在 4 到 16 之間（在 0-255 尺度上），歸一化后分別等于 0.02 和 0.06。我們的 ${\delta }_{max}$ (0.05) 落在此范圍內。

5.2.2 攻擊不可微分、隨機化的輸入變換（Non-Differentiable, Randomized Input Transformations）

不可微分的輸入變換執行梯度混淆，依賴于操縱梯度來成功對抗基于梯度的攻擊者[3]。此外，隨機化的變換增加了攻擊者保證成功的難度。可以通過修改執行梯度混淆的核心防御模塊來規避此類方法，但這顯然不適用于黑盒情況。

在[13]中，探索了幾種輸入變換，包括位深度縮減、JPEG 壓縮和總方差最小化（TVM）。位深度縮減和 JPEG 壓縮是不可微分的，而 TVM 引入了額外的隨機化并且速度相當慢，使得難以迭代。我們證明，由于其無梯度（gradient-free）和多模態（multi-modal）的基于種群特性，GenAttack 可以在黑盒情況下成功對抗這些輸入變換，使其不受梯度混淆的影響。據我們所知，我們是第一個展示能夠繞過此類防御的黑盒算法的工作。我們的結果總結在表 4 中。

對于位深度縮減，減少了 3 位；對于 JPEG 壓縮，質量級別設置為 75，如[13]中所述。GenAttack 能夠在 CIFAR-10 和 ImageNet 數據集上對這兩種不可微分變換都實現高成功率。我們針對 JPEG 壓縮防御的結果的視覺示例如圖 4 所示。

總方差最小化（TVM）帶來了額外的挑戰，因為它不僅不可微分，還引入了隨機化，并且是一個非常緩慢的過程。TVM 隨機丟棄原始圖像中的許多像素（丟棄率為 50%，如[13]），并通過解決去噪優化問題從剩余像素重建輸入圖像。由于隨機化，分類器對同一輸入在每次運行中返回不同的分數，從而迷惑攻擊者。要成功對抗隨機化需要更多迭代，但由于 TVM 處理速度慢，在該防御上進行迭代很困難。

在存在隨機化的設置中，ComputeFitness 函數可以推廣為：

$$ComputeFitness(x)={\mathbb{E}}_r\left[\log f(\mathbf{x},r{)}_t?\log \underset{c\ne t}{\max }f(\mathbf{x},r{)}_c\right]$$

其中 $f(\mathbf{x},r)$ 是帶隨機化防御的模型查詢函數，$r$ 是 TVM 函數的噪聲輸入，GenAttack 仍然可以在黑盒情況下處理這種防御。期望值是通過為每個種群成員查詢模型 $t$ 次（我們使用 $t=32$）來計算的，以在增加查詢數量的代價下獲得魯棒的適應度分數。由于對每個查詢應用 TVM 的計算復雜性，我們僅使用 CIFAR-10 數據集進行了 TVM 實驗，并在 $L_{\infty }=0.15$ 下實現了 70% 的成功率。由于 TVM 引入了較大的隨機化，我們僅當對抗樣本連續三次被分類為目標標簽時才將其計為成功。值得注意的是，除非模型使用變換后的樣本重新訓練[13]，否則 TVM 會顯著降低模型在干凈輸入上的準確率（例如，在我們的 CIFAR-10實驗中，準確率從 80% 下降到 40%）。

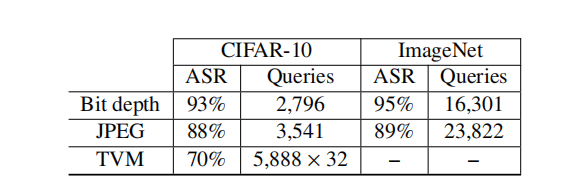
表 4： GenAttack 對不可微分和隨機化輸入變換防御的評估。我們使用 $L_{\infty }=0.05$ 進行位深度實驗，使用 $L_{\infty }=0.15$ 進行 JPEG 和 TVM 實驗。對于 TVM，我們通過進行 $t=32$ 次查詢來計算適應度函數的期望值。

圖 3： GenAttack 針對 InceptionV3 模型 ($L_{\infty }=0.05$) 生成的對抗樣本。左圖：原始圖像，右圖：對抗樣本。

圖 4： GenAttack 針對 JPEG 壓縮防御 ($L_{\infty }=0.15$) 生成的對抗樣本。左圖：原始圖像，右圖：對抗樣本。

• 與 ZOO 和 C&W 的比較：由于輸入變換的不可微分性質，基于梯度的攻擊（如 C&W）在不操縱不可微分組件的情況下無法成功，如[3]所討論。在**白盒（white-box）情況下，可以應用這種方法實現高成功率，但在更受限的黑盒（black-box）**情況下不適用。在黑盒設置中，ZOO 針對 ImageNet 上的不可微分位深度縮減和 JPEG 壓縮防御僅實現了 8% 和 0% 的成功率，再次證明了其實用性不足。

5.3 超參數值選擇

由于遺傳算法傳統上對超參數值的選擇（例如種群大小、變異率等）敏感，我們在查詢效率的背景下討論了這種影響，這導致了我們在第 5 節列出的超參數值的選擇。

• 種群大小（Population size）：較大的種群大小允許增加種群多樣性，從而在更少的迭代次數內改進對搜索空間的探索。然而，由于評估每個種群成員的成本是一次查詢，在選擇大種群大小以加速算法成功（就迭代次數而言）與花費的總查詢次數之間存在權衡。圖 5 展示了這種權衡。在一組 20 張圖像上，我們記錄了在不同種群大小選擇下成功所需的平均查詢次數以及迭代次數。從這個實驗中，我們得出結論，相對較小的種群大小（6）是平衡收斂速度和查詢次數的一個合理選擇。
• 變異率（Mutation rate）：對于變異率 $\rho$，我們發現如果使用根據第 4 節公式 (1) 和 (2) 逐漸衰減的自適應變異率，可以獲得最佳結果。如圖 6 所示，該方法優于固定值的變異率。實際上，自適應變異率通過在初始階段鼓勵探索，然后在算法接近最優解收斂時逐漸增加利用（exploitation）率，從而在探索（exploration）和利用（exploitation）之間取得平衡。
  

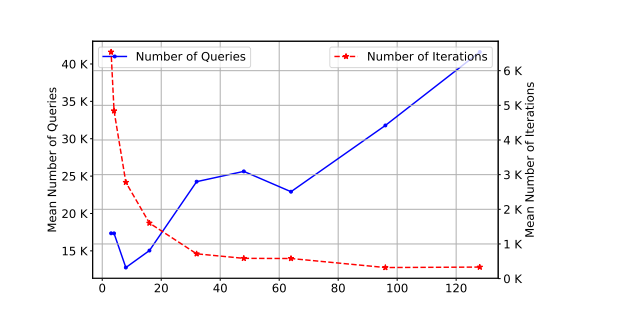
圖 5： 種群大小選擇對收斂速度和查詢次數的影響。

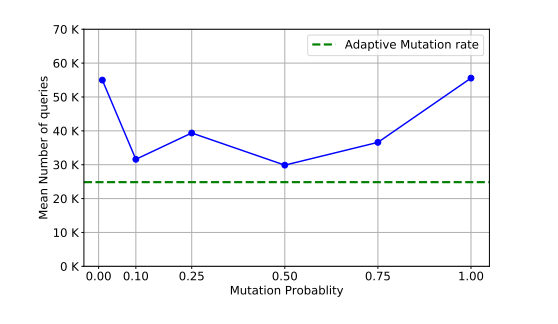
圖 6： 變異概率對成功所需查詢次數的影響。

6. 結論

GenAttack 是一種強大且高效的黑盒攻擊方法，它通過采用基于種群的遺傳算法，實現了無梯度優化方案。我們通過攻擊訓練良好的 MNIST、CIFAR-10 和 ImageNet 模型來評估 GenAttack，發現 GenAttack 能夠以比先前最先進方法顯著更少的查詢量成功地對這些模型執行有目標的黑盒攻擊，并且能夠在 ImageNet 上實現高成功率（這是先前方法無法擴展到的）。此外，我們證明 GenAttack 可以成功地攻擊集成對抗訓練（最先進的 ImageNet 防御），且查詢量的增加有限。最后，我們表明，由于其無梯度的特性，GenAttack 可以成功對抗梯度混淆，具體通過評估其對不可微分輸入變換的有效性來證明，并且甚至可以通過將適應度函數推廣為計算變換的期望來成功對抗隨機化的防御。據我們所知，這是首次展示能夠成功對抗這些最先進防御的黑盒攻擊。我們的結果表明，基于種群的優化為研究有效的無梯度黑盒攻擊開辟了一個有前景的研究方向。

致謝

本研究部分由美國陸軍研究實驗室（U.S. Army Research Laboratory）和英國國防部（UK Ministry of Defence）在協議號 W911NF-16-3-0001 下支持，由美國國家科學基金會（National Science Foundation）在獎項 # CNS-1705135、IIS-1719097 和 OAC-1640813 下支持，以及由美國國立衛生研究院移動傳感器數據到知識中心（NIH Center of Excellence for Mobile Sensor Data-to-Knowledge, MD2K）在獎項 1-U54EB020404-01 下支持。本材料中的任何發現均為作者的觀點，并不反映上述任何資助機構的觀點。盡管此處有版權標記，美國和英國政府仍被授權為政府目的復制和分發再版。

參考文獻

• [1] Moustafa Alzantot, Bharathan Balaji, and Mani Srivastava. 2017. Did you hear that? adversarial examples against automatic speech recognition. Machine Deception Workshop, Neural Information Processing Systems (NIPS) 2017 (2017).
• [2] Moustafa Alzantot, Yash Sharma, Ahmed Elgohary, Bo-Jhang Ho, Mani Srivastava, and Kai-Wei Chang. 2018. Generating Natural Language Adversarial Examples. EMNLP: Conference on Empirical Methods in Natural Language Processing (2018)
• [3] A. Athalye, N. Carlini, and D. Wagner. 2018. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. arXiv preprint arXiv:1802.00420 (2018).
• [4] A. Athalye, L. Engstrom, A. Ilyas, and K. Kwok. 2017. Synthesizing robust adversarial examples. arXiv preprint arXiv:1707.07397 (2017).
• [5] Dinabandhu Bhandari, CA Murthy, and Sankat K Pal. 1996. Genetic algorithm with elitist model and its convergence. International journal of pattern recognition and artificial intelligence 10, 06 (1996), 731-747.
• [6] Wichard Brendel, Jonas Raubert, and Matthias Bethge. 2018. Decision-based adversarial attacks: Reliable attacks against black-box machine learning models. International Conference on Learning Representations (ICLR) (2018).
• [7] N. Carlini and D. Wagner. 2017. Towards evaluating the robustness of neural networks. arXiv preprint arXiv:1608.04644 (2017).
• [8] P. Y. Chen, Y. Sharma, H. Zhang, J. Yi, and C. Hsieh. 2017. EAD: Elastic-net attacks to deep neural networks via adversarial examples. arXiv preprint arXiv:1709.04114 (2017).
• [9] P. Y. Chen, H. Zhang, Y. Sharma, J. Yi, and C. Hsieh. 2017. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training sub-stitute models. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security. ACM, 15-26.
• [10] J. Deng, W. Dong, R. Socher, J. Li, K. Li, and L. Fei-Fei. 2009. Imagenet: A large-scale hierarchical image database. In Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference on. IEEE, 248-255.
• [11] I. Goodfellow, J. Shlens, and C. Szegedy. 2014. Explaining and harnessing adversarial examples. arXiv preprint arXiv:1412.6572 (2014).
• [12] S. Gu and L. Rigazio. 2014. Towards deep neural network architectures robust to adversarial examples. arXiv preprint arXiv:1412.5068 (2014).
• [13] C. Guo, M. Rana, and L. van der Maaten. 2017. Countering adversarial images using input transformations. arXiv preprint arXiv:1711.00117 (2017).
• [14] A. Ilyas, L. Engstrom, A. Athalye, and J. Lin. 2018. Black-box Adversarial Attacks with Limited Queries and Information. arXiv preprint arXiv:1804.08598 (2018).
• [15] D. Kingma and J. Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
• [16] A. Kurathri, I. Goodfellow, and S. Bengio. 2016. Adversarial examples in the physical world. arXiv preprint arXiv:1607.02535 (2016).
• [17] A. Kurathri, I. Goodfellow, S. Bengio, Y. Dong, F. Liao, M. Liang, T. Pang, J. Zhu, X. Hu, C. Xie, J. Wang, Z. Zhang, Z. Ren, A. Vidal, S. Huang, Y. Zhao, Y. Zhao, Z. Han, X. Long, Y. Berthelotzky, T. Akiba, S. Tokui, and M. Abe. 2018. Adversarial attacks and defences competition. arXiv preprint arXiv:1804.00097 (2018).
• [18] Yanpei Liu, Xinyun Chen, Chang Liu, and Dawn Song. 2018. Delving into transferable adversarial examples and black-box attacks. International Conference on Learning Representations (ICLR) (2018).
• [19] P. H. Lu, P. Y. Chen, K. C. Chen, and C. M. Yu. 2018. On the limitation of MagNet defense against L1-based adversarial examples. arXiv preprint arXiv:1805.00310 (2018).
• [20] A. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu. 2017. Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083 (2017).
• [21] S. Moosavi-Dezfooli, A. Fawzi, and P. Frossard. 2016. Deepfool: a simple and accurate method to fool deep neural networks. In Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).
• [22] N. Papernot, P. McDaniel, I. Goodfellow, S. Jin, Z. B. Celik, and A. Swami. 2017. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security. ACM, 506-519.
• [23] Lukas Schott, Jonas Rauber, Matthias Bethge, and Wichard Brendel. 2019. Towards the first adversarially robust neural network model on MNIST. International Conference on Learning Representations (ICLR) (2019).
• [24] Y. Sharma and P. Y. Chen. 2017. Attacking the Madry defense model with L1-based adversarial examples. arXiv preprint arXiv:1710.10733 (2017).
• [25] Y. Sharma and P. Y. Chen. 2018. Pypassing feature squeezing by increasing adversary strength. arXiv preprint arXiv:1803.06968 (2018).
• [26] Y. Sharma, T. Le, and M. Alzantot. 2018. CAD2.018: Generating Transferable Adversarial Examples. arXiv preprint arXiv:1810.01268 (2018).
• [27] Dong Su, Huan Zhang, Hongse Chen, Jurheng Yi, Pin-Yu Chen, and Yupeng Gao. 2018. Is Robustness the Cost of Accuracy?: A Comprehensive Study on the Robustness of 18 Deep Image Classification Models. In Proceedings of the European Conference on Computer Vision (ECCV). 631-648.
• [28] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich. 2015. Going deeper with convolutions. CVPR.
• [29] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, and I. Goodfellow. 2013. Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199 (2013).
• [30] F. Tramer, A. Kurathri, N. Papernot, D. Boneh, and P. McDaniel. 2017. Ensemble adversarial training: Attacks and Defenses. arXiv preprint arXiv:1705.07204 (2017).
• [31] Chun-Chen Tu, Paishun Ting, Pin-Yu Chen, Sijia Liu, Huan Zhang, Jurfeng Yi, Cho-Jui Hsieh, and Shin-Ming Cheng. 2018. AutoZOOM: Autoencoder-based Zeroth Order Optimization Method for Attacking Black-box Neural Networks. arXiv preprint arXiv:1805.11770 (2018).
• [32] Huan Zhang, Hongse Chen, Zhao Song, Duane Boning, Inderjit S Dhillon, and Cho-Jui Hsieh. 2019. The Limitations of Adversarial Training and the Blind-Spot Attack. International Conference on Learning Representations (ICLR) (2019).