當描述 相對變化量 比 絕對量 更容易時,微分方程就經常用到了。
比如,描述為什么種群數量增加or減少【相對】,比描述為什么它在某個時間點是某個特定值【絕對】更容易。
物理學中,運動經常用力來描述,力–>代表變化狀態的加速度。
常微分方程(ODE):函數有一個自變量;
偏微分方程(PDE):函數有多個自變量。
Nabla算子(也稱為梯度算子,符號為 ?)是一種微分算子(一個向量),其作用于不同的對象有不同的名稱(梯度,散度,旋度)。最早有哈密頓引進,也可叫哈密頓算子。
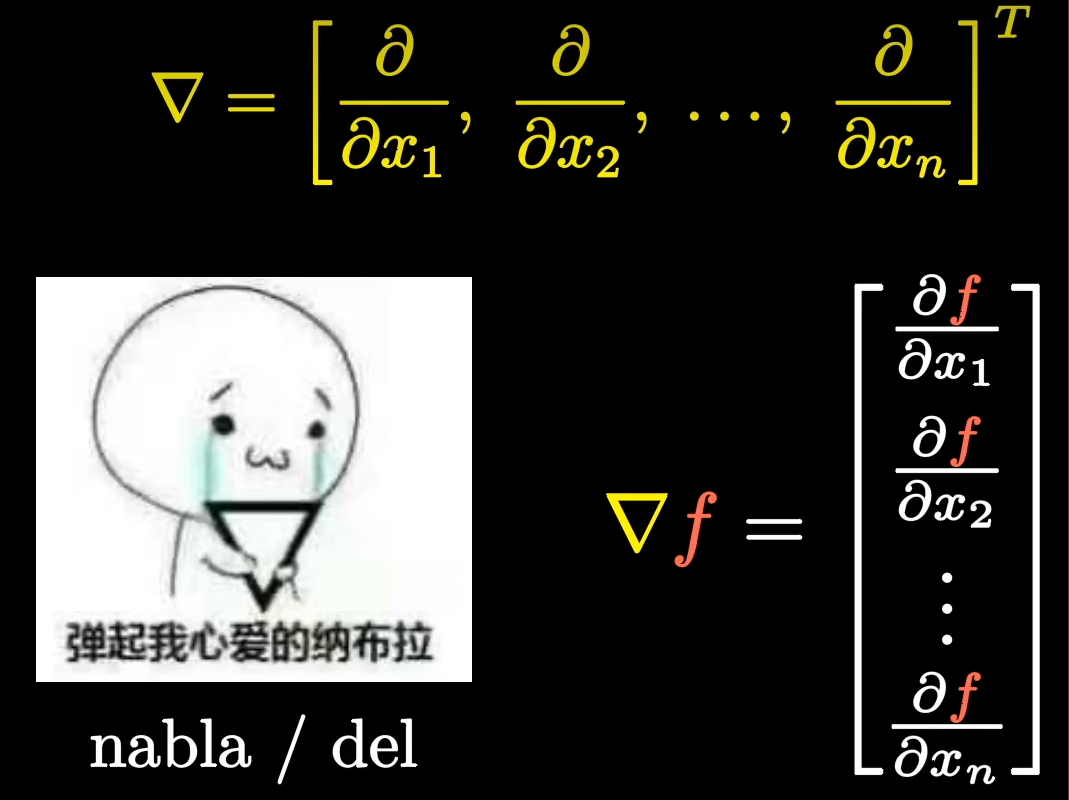
- 梯度:??(表示標量場的梯度,結果是一個向量)。數量場–>向量場,可以看做向量的數量乘法。
- 散度:??A(表示向量場的散度,結果是一個標量)。向量場–>數量場,可以看做向量的內積or點乘。
比如在一個梯度場中,每個方向都是指向函數變化最快的方向:
散度為正,說明它是這個向量場對“源”,有很多點正在遠離此處,那么可以理解為此處是一個“山谷”or最低點;
散度為負,說明它是這個向量場對“匯”,有很多點向它聚集,可以理解為此處是一個“山頂”or最高點。
散度為零,流入與流出相等。- 旋度:?×A(表示向量場的旋度,結果是一個向量),旋渦的方向滿足右手定則。
視頻見nabla算子
拉普拉斯算子,二階微分算子,通常用符號 ?2 表示。求梯度的散度。
有點類似標量值的多變量函數的二階導數,因為 二階導>0,說明是極小值點;二階導<0,說明是極大值點。

視頻見拉普拉斯算子直觀化


)















)

