M2IV: Towards Efficient and Fine-grained Multimodal In Context Learning in Large Vision-Language Models
COLM 2025
why
新興的研究方向:上下文學習(ICL)的效果“向量化”,其核心思想是用transformer內部的向量來替代演示示例。然而,之前的方法(如Task Vector, Function Vector, I2CL等)雖然在一些簡單文本任務上取得了成功,但在處理復雜的多模態任務(如視覺問答VQA)時,普遍存在以下深層次的局限性:
-
無法有效實現跨模態交互:
- 現有的方法,如從最終Token的隱藏狀態提取向量(Hendel et al., 2023),或平均關鍵注意力頭的輸出來計算向量(Todd et al., 2024),在本質上是一種“靜態”的提取-注入模式。例如:對于同一類任務(比如VQA),無論新的查詢QnewQ_{new}Qnew?問的是什么,注入的都是同一個VtaskV_{task}Vtask?
- 這種模式(最終Token提取向量)對于純文本任務(如國家-首都映射)尚可(a),但對于VQA圖像和文本深度融合的復雜任務則效果很差(b)。
- 最終token向量->上下文效果:自回歸語言模型,逐詞預測下一個詞,當處理完一個完整的句子或段落后,最后一個Token的隱藏狀態hlasth_{\text{last}}hlast?聚合和編碼了整個輸入序列的全部信息。它可以被看作是模型對整個句子的“最終思考總結”。
![![[image-164.png|523x250]]](https://i-blog.csdnimg.cn/direct/27e6887bbc044fc781fc369af8f464f8.png)
-
忽略了模型內部不同計算模塊的功能差異:
-
此前的研究普遍將Transformer層視為一個“黑箱”,或者只關注其最終輸出(LIVE)。它們沒有充分利用一個關鍵的洞察:在一個Transformer層中,多頭注意力(MHA)和多層感知器(MLP)扮演著截然不同的角色。MHA更側重于全局信息整合與高級語義關聯,而MLP則負責進行更精細的特征提煉與非線性變換。
![* ![[image-177.png|380x206]]](https://i-blog.csdnimg.cn/direct/a5ef989a83be43ce9d85a2c76d3c4bbe.png)
-
因此,用一個單一的向量或一種單一的注入策略去同等地影響這兩個功能迥異的模塊,是一種粗粒度的干預,限制了模型引導的精度和效果。
-
-
信息蒸餾不足,導致性能隨復雜度增加而快速下降:
- 由于上述兩個理論上的粗糙,現有方法實際訓練中,從演示示例中“蒸餾”出的偏移向量不夠精細和全面。Peng et al. (2024) 提出的LIVE方法雖然開始嘗試通過訓練來優化向量,但論文指出,它仍然忽略了對精細化語義的蒸餾。
- 這導致了一個普遍現象:當任務的復雜性增加時(例如,需要更深層次的邏輯推理或對噪聲更大的視覺信息進行處理),這些方法的性能會迅速下降,甚至不如傳統ICL。
what
為了解決上述問題,論文提出了一個名為 M2IV (Multimodal In-context Vectors) 的框架。
M2IV的工作:進一步細化了任務向量表示,提升多模態上下文的引導能力。
這個框架主要包含兩個部分:
-
M2IV 向量:這是一種經過特殊訓練的、高信息密度的向量。它不是輸入數據,而是一種模型的“行為引導器”。在模型進行推理時,這些向量被直接“注入”到模型內部的網絡層中,像一個“插件”一樣,精確地調整模型的思考和計算過程,使其按照特定任務的邏輯來運作。這種注入是雙分支的,分別針對transformer層中負責不同功能的多頭注意力(MHA)和多層感知器(MLP)模塊,以實現更精細的控制。
![![[image-167.png|1000x352]]](https://i-blog.csdnimg.cn/direct/78e5ee3d885847cbb33c9ecc9e69218d.png)
-
VLibrary (向量庫):這是一個配套的“能力庫”。研究者可以為各種不同的任務(如視覺問答、安全審核、代碼生成等)預先訓練好各自的M2IV向量,并將它們存儲在這個庫中。當需要執行某個特定任務時,只需從庫中取出對應的向量并插入,就可增強模型相關能力。
how
3.1 理論推導
在設計M2IV之前,必須從數學上證明其核心思想——分離并向量化上下文效應——是可行的。論文通過兩個定理的推導來完成這一論證。
1. Transformer中的殘差流
![![[image-162.png|212x258]]](https://i-blog.csdnimg.cn/direct/63a11c4ef2724b43a9ed39785ab98c62.png)
信息在標準Transformer層中是如何流動的。其核心是殘差流,模型內部的主要信息流動。
在一個網絡層lll中,對于輸入序列的第iii個位置:
- MHA計算: 首先,該層的多頭注意力(MHA)模塊以來自上一層的殘差流hl?1ih_{l-1}^ihl?1i?作為輸入,計算出注意力輸出alia_l^iali?。
- ali=MHA(hl?1i;θl)a_l^i = MHA(h_{l-1}^i; θ_l)ali?=MHA(hl?1i?;θl?) (公式2)
- MLP計算: 接著,將原始的殘差流hl?1ih_{l-1}^ihl?1i?與MHA的輸出alia_l^iali?相加,然后將結果送入多層感知器(MLP)模塊,得到MLP的輸出mlim_l^imli?。
- mli=MLP(hl?1i+ali;Wl)m_l^i = MLP(h_{l-1}^i + a_l^i; W_l)mli?=MLP(hl?1i?+ali?;Wl?) (公式3)
- 更新殘差流: 最后,將MHA的輸出alia_l^iali?和MLP的輸出mlim_l^imli?同時加回到原始的殘差流hl?1ih_{l-1}^ihl?1i?上,形成該層最終的輸出hlih_l^ihli?,它將作為下一層的輸入。
- hli=hl?1i+ali+mlih_l^i = h_{l-1}^i + a_l^i + m_l^ihli?=hl?1i?+ali?+mli? (公式4)
這個“加法”結構是關鍵。后續的理論證明,這個加法過程中的alia_l^iali?和mlim_l^imli?(當有上下文時)是可以被分解的。
2. MHA計算可分離性
定理1: Attn(hi,[CTQT]T,[CTQT]T)=ζi?Ψ(hi,C,C)+ηi?Attn(hi,Q,Q)Attn(h^i, [C? Q?]?, [C? Q?]?) = ζ^i ? Ψ(h^i, C, C) + η^i ? Attn(h^i, Q, Q)Attn(hi,[CTQT]T,[CTQT]T)=ζi?Ψ(hi,C,C)+ηi?Attn(hi,Q,Q)
意義:自注意力機制分解為兩部分:僅查詢組件 Attn(hi,Q,Q)(h^{i}, Q, Q)(hi,Q,Q)和上下文增強組件Ψ(hi,C,C)\Psi(h^{i}, C, C)Ψ(hi,C,C)。這種分解突出了 MHA 在動態分配注意力方面的作用,在 ICL 中整合查詢特定的焦點和來自演示的上下文見解。
![![[image-165.png|623x532]]](https://i-blog.csdnimg.cn/direct/5ebac37a574b4690ba15e4356115e01a.png)
- Step 1: 寫出注意力機制的初始公式 (公式14)
對于一個查詢向量hih^ihi和由上下文CCC與查詢QQQ拼接而成的鍵值對,其注意力機制的計算如下:
Attn(hi,[CTQT]T,[CTQT]T)=softmax([dM?1/2hiCT,dM?1/2hiQT])[CQ]Attn(h^i, [C? Q?]?, [C? Q?]?) = softmax([d_M^{-1/2}h^iC?, d_M^{-1/2}h^iQ?]) \begin{bmatrix} C \\ Q \end{bmatrix}Attn(hi,[CTQT]T,[CTQT]T)=softmax([dM?1/2?hiCT,dM?1/2?hiQT])[CQ?]
這里,softmax(?)softmax(?)softmax(?)函數將輸入歸一化為概率分布,dM?1/2d_M^{-1/2}dM?1/2?是用于穩定訓練的縮放因子。 - Step 2: 展開計算 (公式15)
為了展開計算,我們首先定義兩個和項,它們分別代表了對上下文CCC與查詢QQQ部分的指數化注意力分數之和:
sC=∑j=1Cexp(dM?1/2hiCjT)s_C = \sum_{j=1}^{C} exp(d_M^{-1/2}h^iC_j?)sC?=∑j=1C?exp(dM?1/2?hiCjT?)
sQ=∑j=1Iexp(dM?1/2hiQjT)s_Q = \sum_{j=1}^{I} exp(d_M^{-1/2}h^iQ_j?)sQ?=∑j=1I?exp(dM?1/2?hiQjT?)
其中,CjC_jCj?和QjQ_jQj?分別是CCC和QQQ矩陣的第j行。 - Step 3: 注意力輸出的分解 (公式16)
基于上述定義,注意力機制的輸出可以被寫為:
Attn(hi,[CTQT]T,[CTQT]T)=(sC+sQ)?1(exp(dM?1/2hiCT)C+exp(dM?1/2hiQT)Q)Attn(h^i, [C? Q?]?, [C? Q?]?) = (s_C + s_Q)^{-1} (exp(d_M^{-1/2}h^iC?)C + exp(d_M^{-1/2}h^iQ?)Q)Attn(hi,[CTQT]T,[CTQT]T)=(sC?+sQ?)?1(exp(dM?1/2?hiCT)C+exp(dM?1/2?hiQT)Q)
通過引入sCs_CsC?和sQs_QsQ?,我們可以將上式重新組合和分解,得到一個更清晰的結構:
=sC(sC+sQ)?1softmax(dM?1/2hiCT)C+sQ(sC+sQ)?1softmax(dM?1/2hiQT)Q= s_C(s_C + s_Q)^{-1} softmax(d_M^{-1/2}h^iC?)C + s_Q(s_C + s_Q)^{-1} softmax(d_M^{-1/2}h^iQ?)Q=sC?(sC?+sQ?)?1softmax(dM?1/2?hiCT)C+sQ?(sC?+sQ?)?1softmax(dM?1/2?hiQT)Q - Step 4: 最終定義與證明完成 (公式17, 18)
根據上述分析,我們可以定義函數ΨΨΨ以及系數ζiζ^iζi和ηiη^iηi如下:- Ψ(ρq,ρk,ρv):=softmax(dM?1/2ρqρkT)ρv,?(ρq,ρk,ρv)Ψ(ρ_q, ρ_k, ρ_v) := softmax(d_M^{-1/2}ρ_qρ_k?)ρ_v, \quad ?(ρ_q, ρ_k, ρ_v)Ψ(ρq?,ρk?,ρv?):=softmax(dM?1/2?ρq?ρkT?)ρv?,?(ρq?,ρk?,ρv?) (公式17)
- ζi:=sC(sC+sQ)?1,ηi:=sQ(sC+sQ)?1ζ^i := s_C(s_C + s_Q)^{-1}, \quad η^i := s_Q(s_C + s_Q)^{-1}ζi:=sC?(sC?+sQ?)?1,ηi:=sQ?(sC?+sQ?)?1 (公式18)
將這些定義代入分解后的表達式,我們就得到了Theorem 1所要證明的結論。至此,定理證明完畢。
3. MLP計算可分離性
定理2:MLP(aC,Qi)=ζi?ψW(aCi)+ηi?MLP(aQi)MLP(a_{C,Q}^i) = ζ^i ? ψ_W(a_C^i) + η^i ? MLP(a_Q^i)MLP(aC,Qi?)=ζi?ψW?(aCi?)+ηi?MLP(aQi?)
意義:定理 2 表明,MLP 機制分解為兩部分:僅查詢組件 MLP(aQi)(a_{Q}^{i})(aQi?)和上下文增強組件ψW(aCi)\psi_{W}(a_{C}^{i})ψW?(aCi?)。通過加權組合,MLP 從查詢和上下文中提取并保留關鍵特征,使 LVLM 能夠在 ICL 中傳達更聚合細致的表征。

- 前提 (公式19): 基于已經證明的Theorem 1,我們知道存在兩個實數系數ζiζ^iζi和ηiη^iηi,使得MHA的輸出滿足以下關系:
aC,Qi=ζi?aCi+ηi?aQia_{C,Q}^i = ζ^i ? a_C^i + η^i ? a_Q^iaC,Qi?=ζi?aCi?+ηi?aQi?
這里,aC,Qia_{C,Q}^iaC,Qi?是同時考慮上下文和查詢時的MHA輸出,aCia_C^iaCi?和aQia_Q^iaQi?分別是只考慮上下文和只考慮查詢時的MHA輸出。 - 矩陣乘法 (公式20):
我們將等式(19)的兩邊同時在右側乘以MLP層的權重矩陣W,假設MLP層就是一個簡單的線性變換,其作用就是將輸入向量xxx乘以一個權重矩陣WWW
得到以下等式:
aC,QiW=ζi?aCiW+ηi?aQiWa_{C,Q}^iW = ζ^i ? a_C^iW + η^i ? a_Q^iWaC,Qi?W=ζi?aCi?W+ηi?aQi?W - 定義新函數與最終證明 (公式21):
我們定義一個新函數ψW(x):=xWψ_W(x) := xWψW?(x):=xW。通過這個定義,我們可以將等式(20)重寫為:
MLP(aC,Qi)=ζi?ψW(aCi)+ηi?MLP(aQi)MLP(a_{C,Q}^i) = ζ^i ? ψ_W(a_C^i) + η^i ? MLP(a_Q^i)MLP(aC,Qi?)=ζi?ψW?(aCi?)+ηi?MLP(aQi?)
這正是Theorem 2所要證明的形式。至此,定理證明完畢。
4. 最終ICL表示
基于上述分析,本文提出 M2IV 用于多模態 ICL 的細粒度表征。M2IV 為 LVLM 每一層transformer的 MHA 和 MLP 分支分配一個可學習的向量和一個權重因子。具體來說,我們定義:
MHA:Va={v1a,v2a,…,vLa},αa={α1a,α2a,…,αLa};(7)MHA: V^{a}=\left\{v_{1}^{a}, v_{2}^{a}, \ldots, v_{L}^{a}\right\}, \alpha^{a}=\left\{\alpha_{1}^{a}, \alpha_{2}^{a}, \ldots, \alpha_{L}^{a}\right\} ; \quad (7)MHA:Va={v1a?,v2a?,…,vLa?},αa={α1a?,α2a?,…,αLa?};(7)
MLP:Vm={v1m,v2m,…,vLm},αm={α1m,α2m,…,αLm},(8)MLP: V^{m}=\left\{v_{1}^{m}, v_{2}^{m}, \ldots, v_{L}^{m}\right\}, \alpha^{m}=\left\{\alpha_{1}^{m}, \alpha_{2}^{m}, \ldots, \alpha_{L}^{m}\right\}, \quad (8)MLP:Vm={v1m?,v2m?,…,vLm?},αm={α1m?,α2m?,…,αLm?},(8)
其中vla,vlm∈RdMv_{l}^{a}, v_{l}^{m} \in \mathbb{R}^{d_{M}}vla?,vlm?∈RdM?是可學習向量,αla,αlm∈R\alpha_{l}^{a}, \alpha_{l}^{m} \in \mathbb{R}αla?,αlm?∈R是相應的權重因子。M2IV 的完整集合表示為Θ={Va,αa,Vm,αm}\Theta=\left\{V^{a}, \alpha^{a}, V^{m}, \alpha^{m}\right\}Θ={Va,αa,Vm,αm},可以直接注入 LVLM 的殘差流中。更新后的殘差流遞歸定義為對于l=1,…,Ll=1, \ldots, Ll=1,…,L和i=1,…,Ii=1, \ldots, Ii=1,…,I:
hli=hl?1i+(ali+αla?vla)+(mli+αlm?vlm)h_{l}^{i}=h_{l-1}^{i}+\left(a_{l}^{i}+\alpha_{l}^{a} \cdot v_{l}^{a}\right)+\left(m_{l}^{i}+\alpha_{l}^{m} \cdot v_{l}^{m}\right)hli?=hl?1i?+(ali?+αla??vla?)+(mli?+αlm??vlm?)
3.2 訓練實現
M2IV的訓練通過構建在一個自蒸餾框架,該框架由一個教師模型、一個學生模型(兩個模型相中)以及一組損失函數共同構成。
![![[image-167.png|1000x352]]](https://i-blog.csdnimg.cn/direct/7f0546123a254046a2016ca5fd373e2a.png)
1. 自蒸餾框架:教師與學生模型
- 教師模型:
- 輸入: 接收完整的查詢樣本QQQ和nnn個演示示例CCC。執行傳統的Vanilla ICL。
- 作用: 其輸出的概率分布PM(C,Q)P_M(C, Q)PM?(C,Q)被視為“軟標簽”,是學生模型需要模仿的目標。
- 學生模型:
- 輸入: 只接收一個查詢樣本QQQ。
- 工作機制: 在其內部的每一層,通過公式 hli=hl?1i+(ali+αla?vla)+(mli+αlm?vlm)h_l^i = h_{l-1}^i + (a_l^i + α_l^a ? v_l^a) + (m_l^i + α_l^m ? v_l^m)hli?=hl?1i?+(ali?+αla??vla?)+(mli?+αlm??vlm?)進行向量注入。
- 目標: 通過不斷優化M2IV向量ΘΘΘ,使其輸出PM(Q;Θ)P_M(Q; Θ)PM?(Q;Θ)能無限逼近教師模型的輸出PM(C,Q)P_M(C, Q)PM?(C,Q)。
2. 損失函數
蒸餾訓練由三個損失函數共同驅動,它們從不同維度對學生模型進行約束。
- 損失函數: L=λmim?Lmim+λsyn?Lsyn+λsup?LsupL = λ_{mim} ? L_{mim} + λ_{syn} ? L_{syn} + λ_{sup} ? L_{sup}L=λmim??Lmim?+λsyn??Lsyn?+λsup??Lsup?
a. 模仿損失
- 公式: Lmim=T2?DKL(PMT(C,Q)∥PM(Q;Θ)),C∈DC,Q∈DQ\mathcal{L}_{mim }=\mathcal{T}^{2} \cdot \mathbb{D}_{K L}\left(P_{\mathcal{M}}^{\mathcal{T}}(C, Q) \| P_{\mathcal{M}}(Q ; \Theta)\right), C \in \mathcal{D}_{C}, Q \in \mathcal{D}_{Q}Lmim?=T2?DKL?(PMT?(C,Q)∥PM?(Q;Θ)),C∈DC?,Q∈DQ?
- 含義詳解: 減小教師和學生模型的輸出分布
- DKLD_{KL}DKL?: KL散度,衡量兩個概率分布的差異。目標是最小化這個差異。
- PM(C,Q)P_M(C, Q)PM?(C,Q): 教師模型的輸出分布。
- PM(Q;Θ)P_M(Q; Θ)PM?(Q;Θ): 學生模型的輸出分布。
- TTT: 溫度系數。對PM(C,Q)P_{M}(C, Q)PM?(C,Q)做溫度縮放,以促進平滑的知識蒸餾并減輕過度自信,是知識蒸餾的標準技巧。
b. 協同損失
- 公式: Lsyn=∑l=1L(∑i=j(1?Mijl)2+γ?∑i≠jMijl2)\mathcal{L}_{syn }=\sum_{l=1}^{L}\left(\sum_{i=j}\left(1-M_{i j}^{l}\right)^{2}+\gamma \cdot \sum_{i \neq j} M_{i j}^{l^{2}}\right)Lsyn?=∑l=1L?(∑i=j?(1?Mijl?)2+γ?∑i=j?Mijl2?)
- 含義詳解: 增強 MHA 和 MLP 分支之間的一致性和互補性
- 其中Ml=(Zla(Θ))?Zlm(Θ)∈RdM×dMM^{l}=(Z_{l}^{a}(\Theta))^{\top} Z_{l}^{m}(\Theta) \in \mathbb{R}^{d_{M} \times d_{M}}Ml=(Zla?(Θ))?Zlm?(Θ)∈RdM?×dM?是跨視圖相關矩陣,由MHA和MLP分支的輸出計算而來。
- 對角線項 MiiM_{ii}Mii?: 迫使MiiM_{ii}Mii?趨近于1,代表MHA和MLP兩個分支在對應維度上必須目標一致、高度協同。
- 非對角線項 MijM_{ij}Mij?: 迫使MijM_{ij}Mij?趨近于0,代表不同維度之間應該是正交的、不相關的,鼓勵兩個分支學習功能互補,信息不冗余。
- γγγ: 平衡超參數,權衡“協同”與“互補”的重要性。
c. 監督損失
- 公式: Lsup=?∑t=1Tlog?PM(At∣Q,A:<t;Θ),Q∈DQ\mathcal{L}_{sup }=-\sum_{t=1}^{T} \log P_{\mathcal{M}}\left(A_{t} | Q, A_{:<t} ; \Theta\right), Q \in \mathcal{D}_{Q}Lsup?=?∑t=1T?logPM?(At?∣Q,A:<t?;Θ),Q∈DQ?
- 含義詳解: 標準的交叉熵損失,微調必備,使輸出逼近真實的正確答案。
- AtA_tAt?: 真實的正確答案token。
- 目標: 確保學生模型學習模仿絕對正確的答案,不只是模仿教師輸出。
權重設置: 論文在Table 7 中給出了針對每個測試數據集的詳細超參數設置,包括學習率以及所有損失函數的權重λmim,λsyn,λsupλ_{mim}, λ_{syn}, λ_{sup}λmim?,λsyn?,λsup?和協同損失內部的γγγ。較高的λmimλ_{mim}λmim?和λsynλ_{syn}λsyn?表明,在訓練中,學習教師的思考模式和保證內部組件的協同工作,比學習真實的正確回答更重要
權重如何得到:用網格搜索或隨機搜索,試驗出來
![![[截屏2025-07-23 23.07.54.png]]](https://i-blog.csdnimg.cn/direct/e9e0a334704c407b93b3f5ed6bd337c1.png)
3.3 實驗
| 模型 | LLM主干 (大腦) | 連接模塊 (橋梁) | 上下文窗口 (短期記憶) | 核心特點 |
|---|---|---|---|---|
| OpenFlamingov2 | MPT-7B | Perceiver Resampler | 2048 | 高效的信息壓縮,非LLaMA家族 |
| IDEFICS2 | Mistral-7B | MLP + 序列化 | 32768 (32K) | 極強的長上下文能力,靈活的圖文交錯處理 |
| LLaVa-Next | Vicuna-7B | 簡單的MLP | 4096 | 卓越的對話與指令遵循能力,極簡的連接設計 |
1. 性能對比
- 實驗設計:
- 模型: 三種主流LVLM:OpenFlamingov2(9B), IDEFICS2(8B) , LLaVa-Next(7B),這些模型在其 LLM 主干、連接模塊和上下文窗口方面有所不同。
- 訓練方法:采用隨機抽樣作為檢索策略R,將樣本數量shot固定為 16,使用 AdamW 作為優化器。
- 基準數據集: 使用了7個覆蓋不同難度和場景的VQA及ICL基準,如VQAv2, GQA, CVQA, VL-ICL bench等。
- 對比方法:
- Zero-shot: 完全不給任何示例。
- Vanilla ICL (16-shot): 論文的主要對比基線,代表傳統ICL方法。
- 其他向量化方法: 包括非訓練的TV, FV, ICV, I2CL和訓練的LIVE(關鍵同類比較)
- 關鍵結論:
-
1.1 平均性能對比
- 數據解讀: 此表展示了所有方法在三個LVLM上跨七個基準的平均準確率。M2IV的得分在所有任務上均顯著領先。
- 結論1: M2IV比 16-shot 常規 ICL 平均高出 3.74%。
- 結論2: 在 LIVE 落后的基準數據集上分別超過 LIVE 3.52%、4.11% 和 3.72%。
- 超長shot:傳統ICL出現遺忘問題,但M2IV克服遺忘,呈現出持續且顯著的增長。
![![[image-178.png|741x292]]](https://i-blog.csdnimg.cn/direct/d3e2b390b9154d31acaa6a8e7730d31a.png)
-
1.2 分模型性能對比
- 數據解讀: 此表將表1的結果拆分到每個具體的LVLM上。數據顯示,M2IV在總共21組(3個模型 × 7個基準)實驗中,有18組取得了第一名的成績。(2個第二1個第三)
- 關鍵結論: M2IV的優越性不依賴于特定的模型架構。無論是在OpenFlamingo、IDEFICS2還是LLaVa-Next上,它都能穩定地帶來性能提升,證明了其方法的普適性。
![![[image-171.png|698x527]]](https://i-blog.csdnimg.cn/direct/9273a881086c4877b5d436482381f4be.png)
-
2. 效率對比實驗
- 關鍵實驗:
-
2.1 推理開銷對比
- 數據解讀: 該圖比較了不同方法的計算量(FLOPs)和推理時間。M2IV的計算開銷幾乎與Zero-shot設置完全相同(僅為Zero-shot的0.95x)。相比之下,16-shot ICL的計算量是其17.25倍,推理時間是其8.57倍。
- 關鍵結論: M2IV幾乎完全消除了ICL在推理階段的效率瓶頸,使其應用成本大幅降低,恢復到了接近零樣本的水平。
![![[image-172.png|548x332]]](https://i-blog.csdnimg.cn/direct/ef915cd8e9b84a50926adfe2be78eded.png)
-
2.2 總體成本效益分析
- 數據解讀: 該圖比較了兩種方法的總GPU小時消耗。紅色條是Vanilla ICL進行所有評估所需的總推理時間。橙色和黃色是M2IV的一次性訓練時間加上所有評估的推理時間。
- 關鍵結論: M2IV的總成本(訓練+推理)低于Vanilla ICL僅推理的成本。這意味著M2IV在推理端節省的巨大開銷,完全可以抵消甚至超過其一次性的訓練成本。在需要被反復調用的實際應用場景中,M2IV的成本效益優勢會隨著使用次數的增加而愈發明顯。
![![[image-173.png|526x312]]](https://i-blog.csdnimg.cn/direct/d31ef89fc4ea44a9b575e561283180ec.png)
-
3. 消融實驗
- 關鍵結論:
- 不同組件的貢獻
- 數據解讀: 該表展示了移除M2IV不同組件(如數據處理步驟或損失函數)后的性能變化。其中,abcd是訓練集的檢索策略,主要關注(e), (f), (g)三行。
- 關鍵結論: 協同損失(LsynL_{syn}Lsyn?)是M2IV的靈魂。
- 移除模仿損失(LmimL_{mim}Lmim?)或監督損失(LsupL_{sup}Lsup?)后,性能有所下降,但尚可接受。
- 然而,一旦移除協同損失(LsynL_{syn}Lsyn?),模型性能出現了斷崖式下跌,平均準確率暴跌了13.00%
- 這個結果證明,強制MHA和MLP兩個分支協同工作(對角線最大化)且分工互補(非對角線最小化)的設計,是M2I![[image-170.png]]V能夠實現精細化語義蒸餾、超越所有同類方法的關鍵所在。
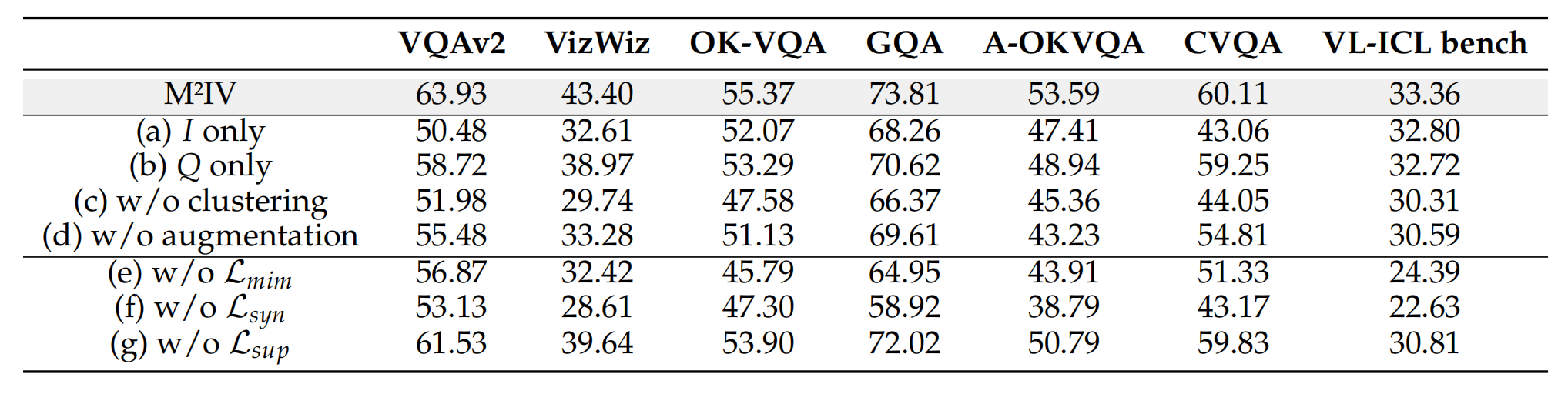
- 不同組件的貢獻
4. 魯棒性與泛化能力實驗
- 關鍵證據與結論:
-
4.1 對不同Shot數的魯棒性
- 數據解讀: 該圖展示了在不同shot數(2, 4, …, 256)下,M2IV相比基線的性能提升值(GAP)。
- 關鍵結論: M2IV在所有shot數下都表現更優(GAP始終為正)。特別是在2-shot和4-shot的少樣本場景下,性能提升最為顯著。這表明M2IV能更有效地從極少量的信息中提煉出任務的本質,適合現實世界數據稀疏的場景。
![![[image-174.png|528x342]]](https://i-blog.csdnimg.cn/direct/da8ec4ddbd9e42bdaf8fed536163e69e.png)
-
4.2 對不同檢索策略的魯棒性
- 數據解讀: 該圖展示了在使用不同檢索方法(如隨機采樣RS、圖像相似度I2I)為Vanilla ICL挑選演示示例時,M2IV帶來的性能增益(淺色部分)。
- 關鍵結論: M2IV在所有策略下都帶來了顯著提升,并且在最差的策略(如I2I,橙色)下,其性能增益是最大的。這說明M2IV具有強大的糾錯和抗干擾能力。即使給它的“教師”(Vanilla ICL)提供的是有偏差或有誤導性的示例,M2IV的訓練過程依然能從中過濾噪聲,學習到正確的任務邏輯。
![![[image-175.png|495x335]]](https://i-blog.csdnimg.cn/direct/f145a2ac479a47e4834364b2c6c8758f.png)
-
5. 靈活性與應用潛力實驗
- 關鍵證據與結論:
- 層級化精確注入
- 數據解讀: 在一個需要關注圖像細節的VQA任務中,研究者們嘗試將M2IV只注入到模型的部分層。結果發現,只注入模型的前10層(通常負責提取基礎視覺特征的淺層網絡)時,性能甚至超過了對所有層進行注入。
- 關鍵結論: 證明了M2IV是一個可以精確引導的工具。我們可以根據任務需求,選擇性地增強模型在特定處理階段(如早期視覺感知、中期語義融合或晚期邏輯推理)的能力。這極大地拓展了M2IV的應用想象空間。
![![[image-176.png|635x241]]](https://i-blog.csdnimg.cn/direct/de2dc9ccaf5449d5bc6c857ed5bef5d2.png)
- 層級化精確注入













)



)
