LeetCode11~30題解

LeetCode11.盛水最多的容器：

題目描述：

給定一個長度為 n 的整數數組 height 。有 n 條垂線，第 i 條線的兩個端點是 (i, 0) 和 (i, height[i]) 。

找出其中的兩條線，使得它們與 x 軸共同構成的容器可以容納最多的水。

返回容器可以儲存的最大水量。

說明：你不能傾斜容器。

示例 1：
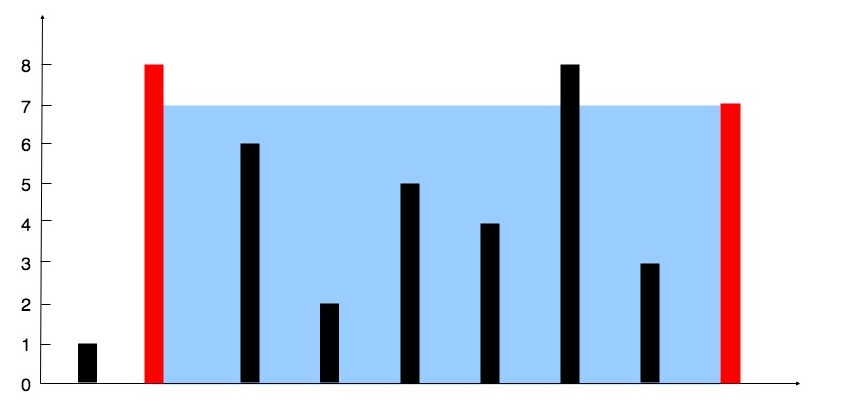
微信截圖_20241028194434.png
輸入：[1,8,6,2,5,4,8,3,7]
輸出：49
解釋：圖中垂直線代表輸入數組 [1,8,6,2,5,4,8,3,7]。在此情況下，容器能夠容納水（表示為藍色部分）的最大值為 49。

示例 2：
輸入：height = [1,1]
輸出：1

提示：
n == height.length
2 <= n <= 10^5
0 <= height[i] <= 10^4

思路：

貪心思想：使用雙指針分別從頭和尾開始，每次計算比較兩個指針的高度，將較小的往中間移一個位置，每次保留最大的裝水體積

證明：

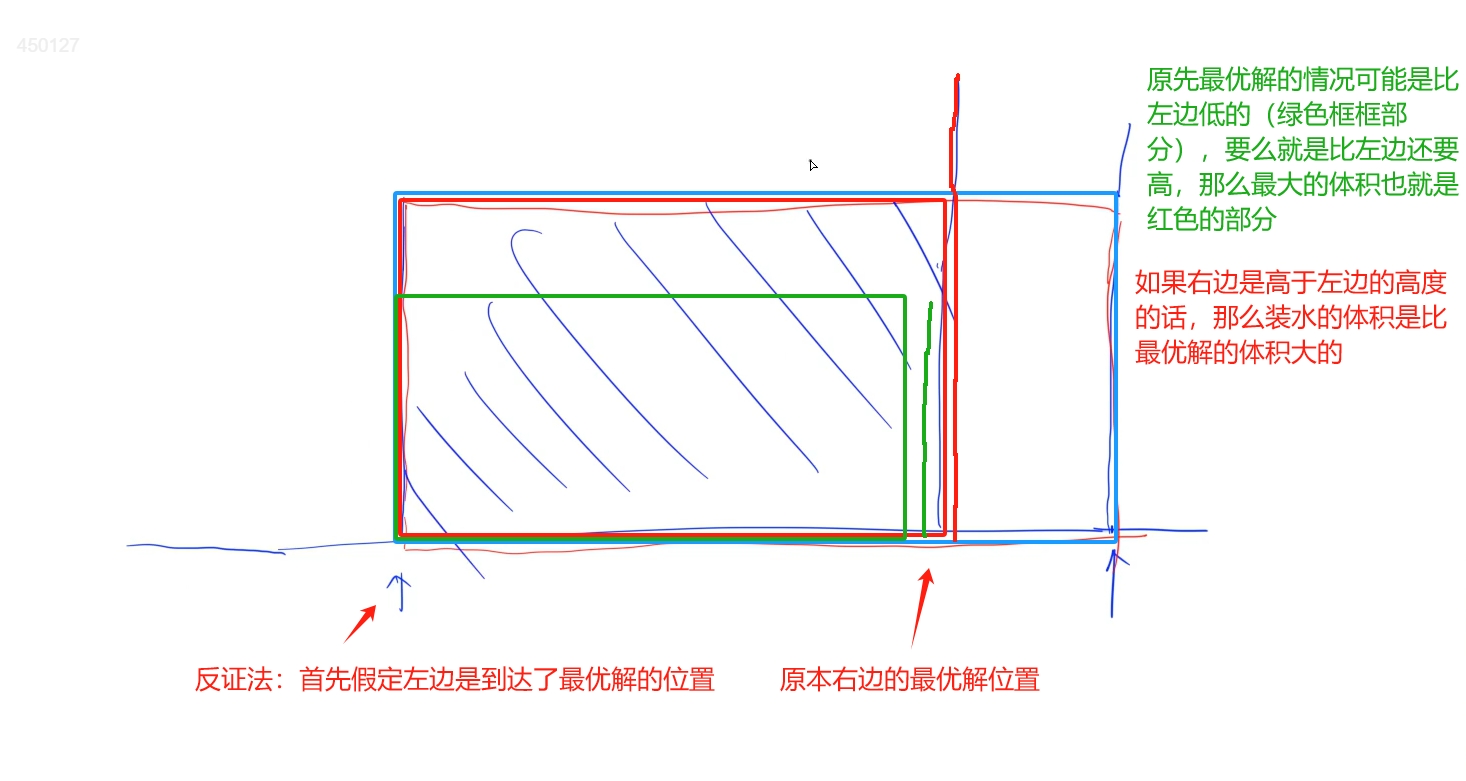
微信圖片編輯_20241028194220.jpg

代碼：

class Solution {
public:int maxArea(vector<int>& height) {int res = 0;for(int i = 0, j = height.size() - 1; i < j; ){res = max(res, min(height[i], height[j]) * (j - i));if(height[i] > height[j]) j--;else i++;}return res;}
};

LeetCode12.整數轉羅馬數字：

題目描述：

七個不同的符號代表羅馬數字，其值如下：

符號:值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
羅馬數字是通過添加從最高到最低的小數位值的轉換而形成的。將小數位值轉換為羅馬數字有以下規則：

如果該值不是以 4 或 9 開頭，請選擇可以從輸入中減去的最大值的符號，將該符號附加到結果，減去其值，然后將其余部分轉換為羅馬數字。
如果該值以 4 或 9 開頭，使用減法形式，表示從以下符號中減去一個符號，例如 4 是 5 (V) 減 1 (I): IV ，9 是 10 (X) 減 1 (I)：IX。僅使用以下減法形式：4 (IV)，9 (IX)，40 (XL)，90 (XC)，400 (CD) 和 900 (CM)。
只有 10 的次方（I, X, C, M）最多可以連續附加 3 次以代表 10 的倍數。你不能多次附加 5 (V)，50 (L) 或 500 (D)。如果需要將符號附加4次，請使用減法形式。

給定一個整數，將其轉換為羅馬數字。

示例 1：
輸入：num = 3749
輸出： “MMMDCCXLIX”
解釋：
3000 = MMM 由于 1000 (M) + 1000 (M) + 1000 (M)
700 = DCC 由于 500 (D) + 100 ? + 100 ?
40 = XL 由于 50 (L) 減 10 (X)
9 = IX 由于 10 (X) 減 1 (I)
注意：49 不是 50 (L) 減 1 (I) 因為轉換是基于小數位

示例 2：
輸入：num = 58
輸出：“LVIII”
解釋：
50 = L
8 = VIII

示例 3：
輸入：num = 1994
輸出：“MCMXCIV”
解釋：
1000 = M
900 = CM
90 = XC
4 = IV

提示：
1 <= num <= 3999

思路：找規律：

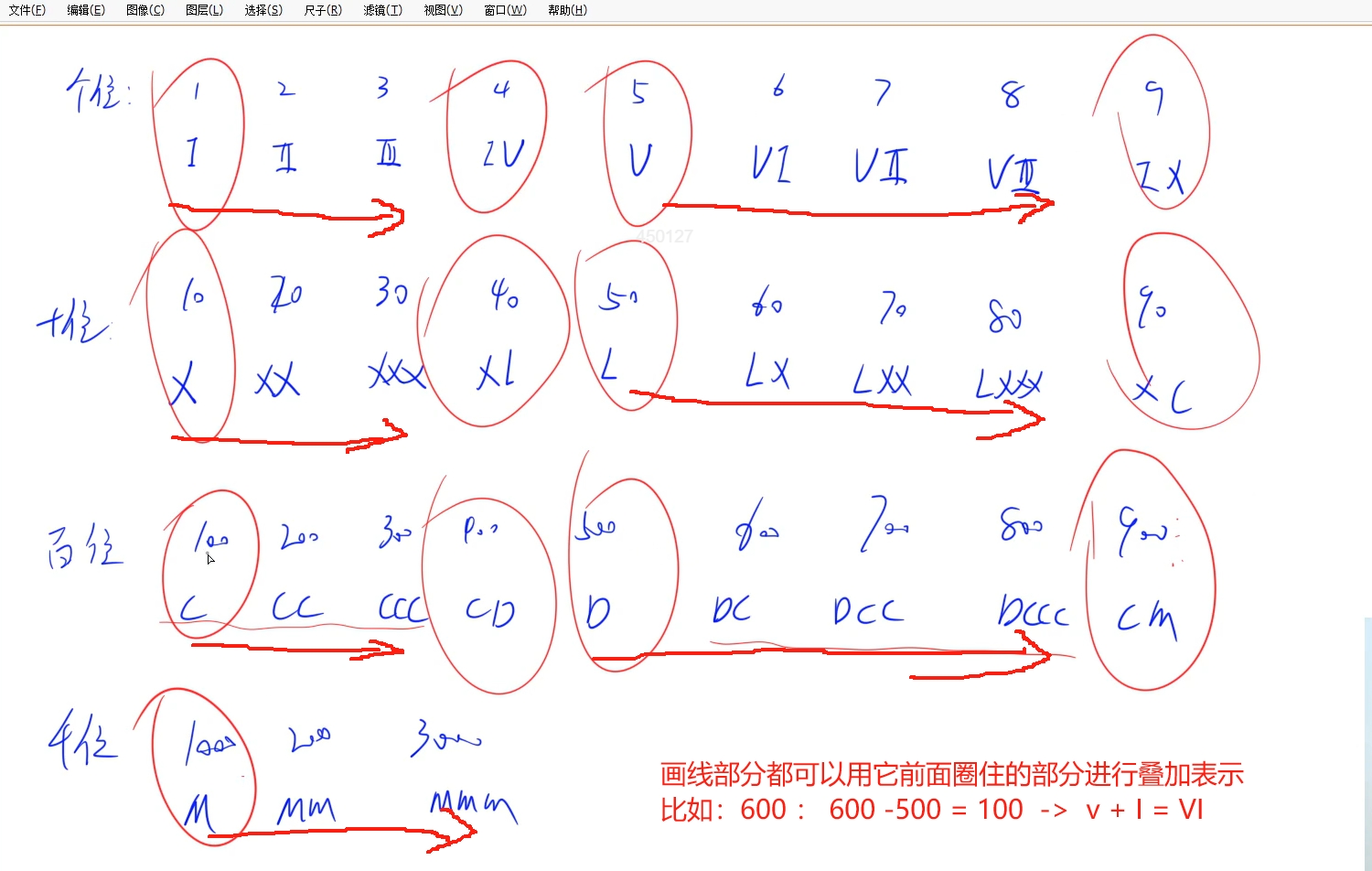
微信圖片編輯_20241028203353.jpg

這樣的話從高位往下依次減，只要將圈住的部分用數組存起來，每次找到對應的數值轉換成字符串之后，再原有基礎上減去當前數值，然后繼續往下找能減的部分繼續減并轉換。

代碼：

class Solution {
public:string intToRoman(int num) {int values[] = {1000,900, 500, 400, 100,90, 50, 40, 10,9, 5, 4, 1};string reps[] = {"M","CM", "D", "CD", "C","XC", "L", "XL", "X","IX", "V", "IV", "I"};string res;for(int i = 0; i < 13; i++){while(num >= values[i]){num -= values[i];res += reps[i];}}return res;}
};

LeetCode13. 羅馬數字轉整數：

題目描述：

羅馬數字包含以下七種字符: I， V， X， L，C，D 和 M。

字符數值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如，羅馬數字 2 寫做 II ，即為兩個并列的 1 。12 寫做 XII ，即為 X + II 。 27 寫做 XXVII, 即為 XX + V + II 。

通常情況下，羅馬數字中小的數字在大的數字的右邊。但也存在特例，例如 4 不寫做 IIII，而是 IV。數字 1 在數字 5 的左邊，所表示的數等于大數 5 減小數 1 得到的數值 4 。同樣地，數字 9 表示為 IX。這個特殊的規則只適用于以下六種情況：

I 可以放在 V (5) 和 X (10) 的左邊，來表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左邊，來表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左邊，來表示 400 和 900。
給定一個羅馬數字，將其轉換成整數。

示例 1:
輸入: s = “III”
輸出: 3

示例 2:
輸入: s = “IV”
輸出: 4

示例 3:
輸入: s = “IX”
輸出: 9

示例 4:
輸入: s = “LVIII”
輸出: 58
解釋: L = 50, V= 5, III = 3.

示例 5:
輸入: s = “MCMXCIV”
輸出: 1994
解釋: M = 1000, CM = 900, XC = 90, IV = 4.

提示：

1 <= s.length <= 15
s 僅含字符 (‘I’, ‘V’, ‘X’, ‘L’, ‘C’, ‘D’, ‘M’)
題目數據保證 s 是一個有效的羅馬數字，且表示整數在范圍 [1, 3999] 內
題目所給測試用例皆符合羅馬數字書寫規則，不會出現跨位等情況。
IL 和 IM 這樣的例子并不符合題目要求，49 應該寫作 XLIX，999 應該寫作 CMXCIX 。
關于羅馬數字的詳盡書寫規則，可以參考羅馬數字 - 百度百科。

思路：

找潛在規律可以發現：在I， V，X， L，C， D， M這些基本的羅馬數字之間
只要前面的羅馬字符代表的數值大于當前代表的數值，就可以直接將當前字符代表的數值加到后面，而 IV， IX， XL， XC， CD， CM這幾個羅馬數字可以發現，前面的單獨字符都比后面的字符所代表的數值小，而后者代表數值減去前者代表數值剛好為它本身代表的數值，所以總結發現，我們只需要判斷前后兩個字符單獨代表的數值大小，就能直接對每個字符進行加減運算

實現方式：將單獨的羅馬字符以及它表示的數值映射到hash表中，依次遍歷羅馬數字的每個字符，找到hash表中對應的數值，對比前后兩個字符表示的數值，進行加減即可。

微信圖片_20241030184753.png

代碼：

class Solution {
public:int romanToInt(string s) {unordered_map<char, int> hash;hash['I'] = 1, hash['V'] = 5;hash['X'] = 10, hash['L'] = 50;hash['C'] = 100, hash['D'] = 500;hash['M'] = 1000;int res = 0;for(int i = 0; i < s.size(); i++){//如果i的后面有字符，并且代表的數值小于后面的字符代表數值if(i + 1 < s.size() && hash[s[i]] < hash[s[i + 1]]){//那么減去代表數值res -= hash[s[i]];}//否則加上代表數值else  res += hash[s[i]];}return res;}
};

純享版：

class Solution {
public:int romanToInt(string s) {unordered_map<char, int> hash;hash['I'] = 1, hash['V'] = 5;hash['X'] = 10, hash['L'] = 50;hash['C'] = 100, hash['D'] = 500;hash['M'] = 1000;int ans = 0;for(int i = 0; i < s.size(); i++){if(i + 1 < s.size() && hash[s[i]] < hash[s[i + 1]]){ans -= hash[s[i]];}else ans += hash[s[i]];}return ans;}
};

LeetCode14.最長公共前綴：

題目描述：

編寫一個函數來查找字符串數組中的最長公共前綴。

如果不存在公共前綴，返回空字符串 “”。

示例 1：
輸入：strs = [“flower”,“flow”,“flight”]
輸出：“fl”

示例 2：
輸入：strs = [“dog”,“racecar”,“car”]
輸出：“”
解釋：輸入不存在公共前綴。

提示：

1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 僅由小寫英文字母組成

思路：

從第一個字符開始依次對比每個字符串的每個字符，全能比對上就將當前字符加入答案子串中

注意：

這里加&符是為了減少時間消耗，否則的話每次循環復制一遍整個數組，時間復雜度會上升

代碼：

class Solution {
public:string longestCommonPrefix(vector<string>& strs) {string res;if(strs.empty()) return res;//從第一個字符開始遍歷for(int i = 0; i <= 200; i++){//如果i大于第一個字符串的長度了，那么后面也就沒必要繼續了if(i >= strs[0].size()) return res;//每次取第一個字符串的第i個字符char c = strs[0][i];for(auto& str : strs){//跟每一個字符串進行比對，如果字符串長度小于i那么肯定不用繼續了，或者說第i個字符匹配不上if(str.size() <= i || str[i] != c){return res;}}//能比對上就在答案子串里將當前字符加上res += c;}return res;}
};

純享版：

class Solution {
public:string longestCommonPrefix(vector<string>& strs) {string res;if(strs.empty()) return res;for(int i = 0; i <= 200; i++){if(i >= strs[0].size()) return res;char c = strs[0][i];for(auto& str : strs){if(str.size() <= i || str[i] != c){return res;}}res += c;}return res;}

LeetCode15.三數之和：

題目描述：

給你一個整數數組 nums ，判斷是否存在三元組 [nums[i], nums[j], nums[k]] 滿足 i != j、i != k 且 j != k ，同時還滿足 nums[i] + nums[j] + nums[k] == 0 。請你返回所有和為 0 且不重復的三元組。

注意：答案中不可以包含重復的三元組。

示例 1：
輸入：nums = [-1,0,1,2,-1,-4]
輸出：[[-1,-1,2],[-1,0,1]]
解釋：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元組是 [-1,0,1] 和 [-1,-1,2] 。
注意，輸出的順序和三元組的順序并不重要。

示例 2：
輸入：nums = [0,1,1]
輸出：[]
解釋：唯一可能的三元組和不為 0 。

示例 3：
輸入：nums = [0,0,0]
輸出：[[0,0,0]]
解釋：唯一可能的三元組和為 0 。

提示：

3 <= nums.length <= 3000
-105 <= nums[i] <= 105

思路：

先從小到大排序，然后先固定最小的那個數nums[i]，再使用雙指針將后面的兩個數確定下來，第二個數nums[j]從第一個數nums[i]后面開始，第三個數nums[k]從最后面開始，每次找到能滿足nums[i] + nums[j] + nums[k] >= 0最小的nums[k]三個數的組合，過程中會發現當nums[j]往后遍歷時，滿足條件的nums[k]會往前挪，兩者(j ,k)都具有單調性，使用雙指針算法可以極大優化時間復雜度，將原本O(n ^2)變為O(2n)時間復雜度。

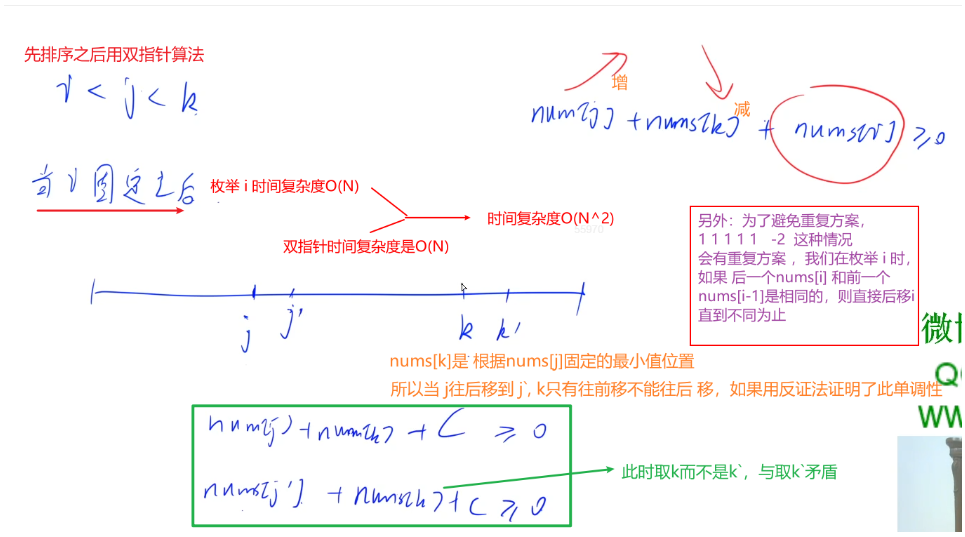
微信圖片_20241031184743.png

代碼：

class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> res;//先進行排序sort(nums.begin(), nums.end());//先將第一個數固定下來for(int i = 0; i < nums.size(); i++){//避免找到重復的方案， 因為已經排序了，nums[i]也固定了， 后面兩個數肯定比nums[i]大//而且nums[i]的方案后面已經全部考慮了if(i && nums[i] == nums[i - 1]) continue;//雙指針算法：  可以發現，j 從i開始的話，只會逐漸增大， 而k從后往前開始會逐漸減小，具有單調性，使用雙指針算法可以極大優化時間復雜度，將原本O(N ^2)變為O(2n)//j：表示第二個數， 從i后面開始找//k: 表示第三個數，從最后面往前找//j < k : 兩個指針不能重疊for(int j = i + 1, k = nums.size() - 1; j < k; j++){//這里的j和i一樣需要排除重復方案if(j > i + 1 && nums[j] == nums[j - 1]) continue;//找到三個數相加大于零的最小的k//如果k的下一個數沒有和j重疊，并且三個數之和大于零就往前挪一位，//因為從小到大排序了，所以越往前挪越接近0while(j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= 0) k--;//看三個數之和是否滿足條件，滿足就將三個數存到容器中if(nums[i] + nums[j] + nums[k] == 0){res.push_back({nums[i], nums[j], nums[k]});}}}return res;}
};

純享版：


class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> res;sort(nums.begin(), nums.end());for(int i = 0; i < nums.size(); i++){if(i && nums[i] == nums[i - 1]) continue;for(int j = i + 1, k = nums.size() - 1; j < k; j++){if(j > i + 1 && nums[j] == nums[j - 1]) continue;while(j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= 0) k--;if(nums[i] + nums[j] + nums[k] == 0){res.push_back({nums[i], nums[j], nums[k]});}}}return res;}
};

###LeetCode16.最接近的三數之和：
##題目描述：

給你一個長度為 n 的整數數組 nums 和一個目標值 target。請你從 nums 中選出三個整數，使它們的和與 target 最接近。
返回這三個數的和。
假定每組輸入只存在恰好一個解。

示例 1：
輸入：nums = [-1,2,1,-4], target = 1
輸出：2
解釋：與 target 最接近的和是 2 (-1 + 2 + 1 = 2)。

示例 2：
輸入：nums = [0,0,0], target = 1
輸出：0
解釋：與 target 最接近的和是 0（0 + 0 + 0 = 0）。

提示：

3 <= nums.length <= 1000
-1000 <= nums[i] <= 1000
-10^4 <= target <= 10^4

##思路：這里跟LeetCode15題思路一致，不過要注意細節方面處理，要考慮最接近target的和，那么有可能是小于target也有可能是大于target，因此要將三數之和與target的差值進行比較，留下最小差的和，

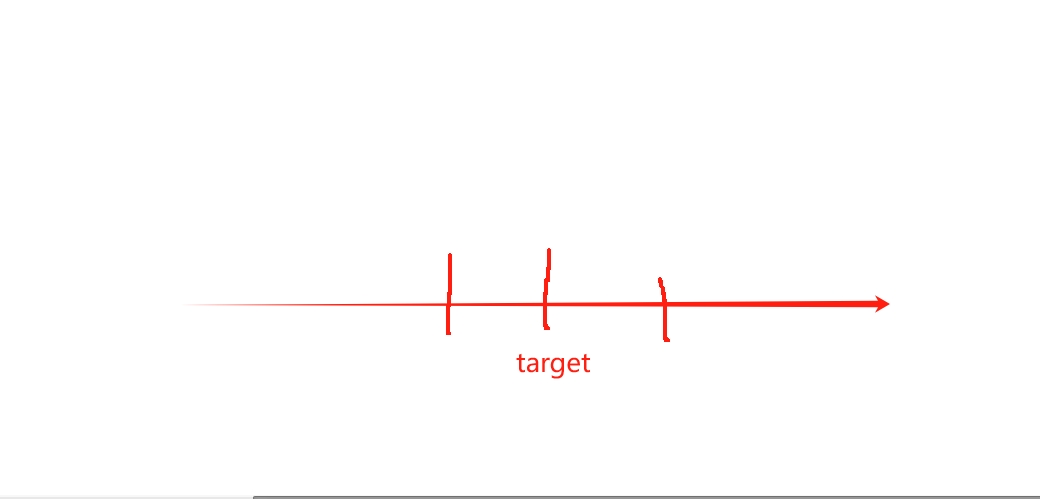
微信截圖_20241031203233.png

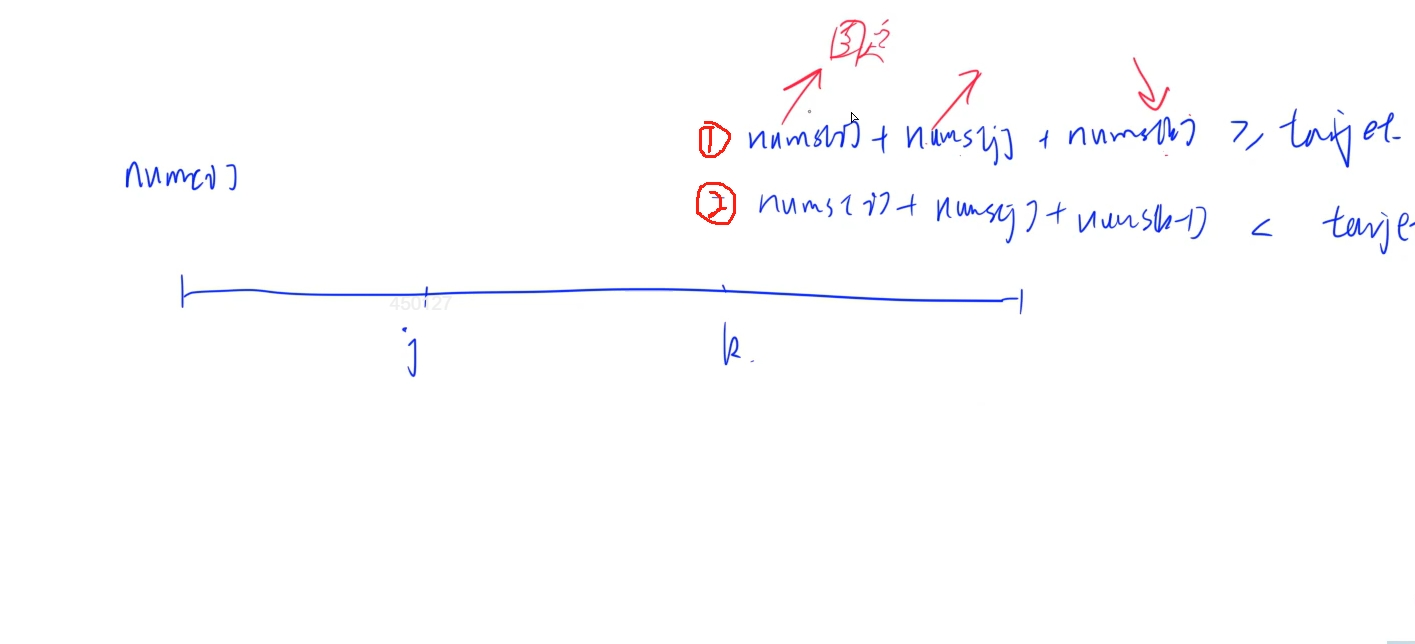
微信圖片編輯_20241031203121.jpg

##代碼：

class Solution {
public:int threeSumClosest(vector<int>& nums, int target) {sort(nums.begin(), nums.end());pair<int, int> res(INT_MAX, INT_MAX);for(int i = 0; i < nums.size(); i++){for(int j = i + 1, k = nums.size() - 1; j < k; j++){while(k - 1 > j && nums[i] + nums[j] + nums[k - 1] >= target) k--;//第一種是nums[i] + nums[j] + nums[k] >= target 的情況int s = nums[i] + nums[j] + nums[k];//記錄最接近target的和，這里有可能會出現所有和都小于target的情況，所以使用absres = min(res, make_pair(abs(s - target), s));//nums[i] + nums[j] + nums[k] < target 的情況//因為第一種情況將nums[k] 逼到三個數最靠近target的情況，//如果nums[k] + nums[i] + nums[j] 是最接近大于等于target的，那么nums[k - 1] + nums[i] + nums[j] 肯定是小于target的if(k - 1 > j){s = nums[i]  + nums[j] + nums[k - 1];res = min(res, make_pair(target - s, s));}}}return res.second;}
};

##純享版：

class Solution {
public:int threeSumClosest(vector<int>& nums, int target) {sort(nums.begin(), nums.end());pair<int, int> res(INT_MAX, INT_MAX);for(int i = 0; i < nums.size(); i++){for(int j = i + 1, k = nums.size() - 1; j < k; j++){while(j < k - 1 && nums[i] + nums[j] + nums[k - 1] >= target) k--;int s = nums[i] + nums[j] + nums[k];res = min(res, make_pair(abs(s - target), s));if(j < k - 1){int s = nums[i] + nums[j] + nums[k - 1];res = min(res, make_pair(target - s, s));}}}return res.second;}
};

LeetCode17.電話號碼的數字組合：

題目描述：

給定一個僅包含數字 2-9 的字符串，返回所有它能表示的字母組合。答案可以按任意順序返回。
給出數字到字母的映射如下（與電話按鍵相同）。注意 1 不對應任何字母。
微信截圖_20241102200052.png

示例 1：
輸入：digits = “23”
輸出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

示例 2：
輸入：digits = “”
輸出：[]

示例 3：
輸入：digits = “2”
輸出：[“a”,“b”,“c”]

提示：
0 <= digits.length <= 4
digits[i] 是范圍 [‘2’, ‘9’] 的一個數字。

思路

根據題目描述，將每位數字對應的字母排列起來，也就是依次找到每位數字對應的字母，分別取一個字符進行排列(排列組合問題)，有點類似全排列，用dfs算法：深度優先遍歷
##注意：只要是涉及到排列組合問題，只要能找到對應的排列數，先考慮dfs能不能做。
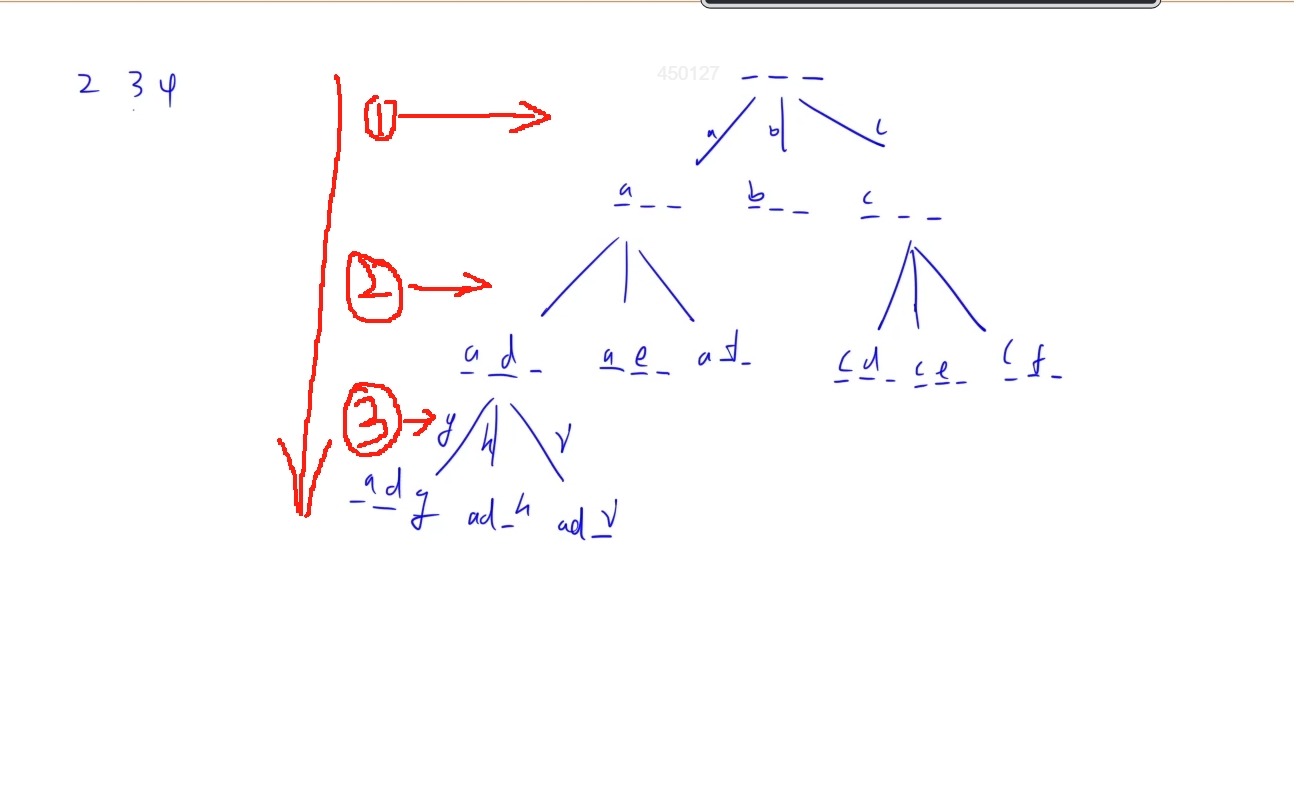
微信圖片編輯_20241102200219.jpg

代碼：

class Solution {
public:
vector<string> ans;
string strs[10] = {"", "", "abc", "def", "ghi", "jkl", "mno","pqrs", "tuv", "wxyz"
};vector<string> letterCombinations(string digits) {if(digits.empty()) return ans;dfs(digits, 0, "");return ans;       }void dfs(string&digits, int u, string path){//path存方案：表示每次的路徑//u表示當前是第幾位//如果u == digits.size() 說明已經排列好了， 將當前走的路徑放入ans里if(u == digits.size()) ans.push_back(path);else{//取出當前位代表的每一個字符， 分別遞歸下去，直到將所有位全部排完for(auto c : strs[digits[u] - '0']){dfs(digits, u + 1, path + c);}}}
};

純享版：

class Solution {
public:vector<string> res;string strs[10] = {"", "", "abc",  "def","ghi", "jkl", "mno","pqrs", "tuv", "wxyz"};vector<string> letterCombinations(string digits) {if(digits.empty()) return res;dfs(digits, 0, "");return res;}void dfs(string& digits, int u, string path){if(u == digits.size()) res.push_back(path);else{for(auto c : strs[digits[u] - '0']){dfs(digits, u + 1, path + c);}}}
};

LeetCode18.四數之和：

題目描述：

給你一個由 n 個整數組成的數組 nums ，和一個目標值 target 。請你找出并返回滿足下述全部條件且不重復的四元組 [nums[a], nums[b], nums[c], nums[d]] （若兩個四元組元素一一對應，則認為兩個四元組重復）：

0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按任意順序返回答案。

示例 1：
輸入：nums = [1,0,-1,0,-2,2], target = 0
輸出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：
輸入：nums = [2,2,2,2,2], target = 8
輸出：[[2,2,2,2]]

提示：

1 <= nums.length <= 200
-10^9 <= nums[i] <= 10^9
-10^9 <= target <= 10^9

思路：

這里思路跟三數之和一模一樣，只不過使用三層循環，同樣使用雙指針優化，時間復雜度為O(n^2 * 2n)

注意：

這里數值范圍會超過int的取值范圍，所以要使用long long 進行存儲

代碼：

class Solution {
public:typedef long long LL;vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int> >  res;sort(nums.begin(), nums.end());LL num = target;for(int i = 0; i < nums.size(); i++){//cout<<i<<endl;if(i && nums[i] == nums[i - 1])  continue;for(int j = i + 1; j < nums.size(); j++){//cout<<j<<endl;if(j > i + 1 && nums[j] == nums[j - 1]) continue;for(int k = j + 1, u = nums.size() - 1; k < u; k++){if(k > j + 1 && nums[k] == nums[k - 1]) continue;while(k < u - 1 && (LL)(nums[i] + nums[j]) + (LL)(nums[k] + nums[u - 1]) >= num) u--;if((LL)(nums[i] + nums[j]) + (LL)(nums[k] + nums[u]) == num){res.push_back({nums[i], nums[j], nums[k], nums[u]});}}}}return res;}
};

純享版：

LeetCode19.刪除鏈表的倒數第N個節點：

題目描述：

給你一個鏈表，刪除鏈表的倒數第 n 個結點，并且返回鏈表的頭結點。

示例 1：
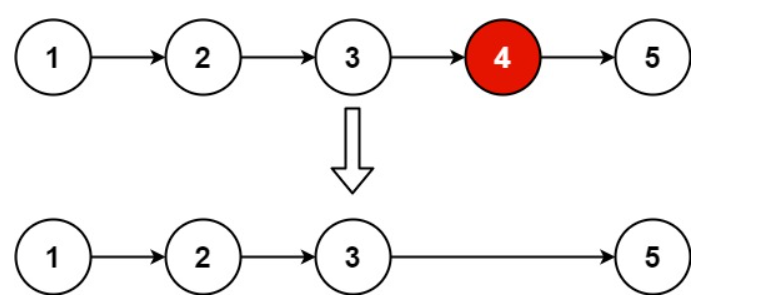
微信圖片_20241103184538.png
輸入：head = [1,2,3,4,5], n = 2
輸出：[1,2,3,5]

示例 2：
輸入：head = [1], n = 1
輸出：[]

示例 3：
輸入：head = [1,2], n = 1
輸出：[1]

提示：
鏈表中結點的數目為 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz

##思路：找到鏈表的倒數第N+1個數，將指針直接指向倒數第N個數的后面，也就是倒數第N+1 個數的next的next
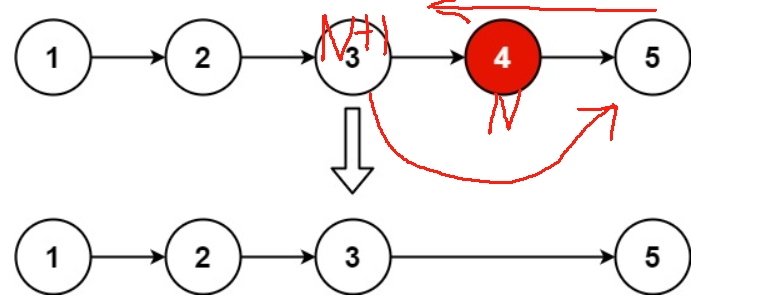
微信圖片編輯_20241103184739.jpg

注意：

一般情況下可以直接跳過倒數第N個數，但有些時候需要刪除第N個節點

注釋代碼：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {//定義虛擬頭節點auto dummy = new ListNode(-1);//將虛擬頭節點連接在原本頭節點前dummy ->next = head;int num = 0;//計算鏈表長度for(auto p = dummy; p; p = p->next) num++;auto p = dummy;//從虛擬頭節點開始，跳到倒數 n + 1個數的位置for(int i = 0; i < num - n - 1; i++) p = p -> next;//讓倒數第n + 1個數直接指向后面的后面， 就能直接跳過倒數第 n個數p -> next = p -> next -> next;//返回鏈表return dummy -> next;}
};

純享版：


/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {auto dummy = new ListNode(-1);dummy -> next = head;int num = 0;for(auto p = dummy; p; p = p -> next) num++;auto p = dummy;for(int i = 0; i < num - n - 1; i++) p = p -> next;p -> next = p -> next -> next;return dummy -> next;}
};

LeetCode20.有效的括號：

題目描述：

給定一個只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判斷字符串是否有效。
有效字符串需滿足：
左括號必須用相同類型的右括號閉合。
左括號必須以正確的順序閉合。
每個右括號都有一個對應的相同類型的左括號。

示例 1：
輸入：s = “()”
輸出：true

示例 2：
輸入：s = “()[]{}”
輸出：true

示例 3：
輸入：s = “(]”
輸出：false

示例 4：
輸入：s = “([])”
輸出：true

提示：
1 <= s.length <= 10^4
s 僅由括號 ‘()[]{}’ 組成

思路：

總思路使用棧，每次將左括號入棧，而右括號則進行匹對，如果每個右括號都能在棧頂找到對應的左括號，每次將匹配的棧頂彈出，最后如果棧中沒有元素那么說明是有效的。這里的算法1是使用取巧方法，查ASCII碼值發現，每對括號的差值都不超過2，如果超過說明是不匹配的，那么直接return false 就行。算法2則是枚舉每種右括號的情況，在棧不為空的情況下進行棧頂比對，匹配上則直接將棧頂彈出

算法1：(取巧)代碼：

class Solution {
public:bool isValid(string s) {stack<char> stk;for(auto c : s){   //如果是右括號，那么將它存入棧中if(c == '{' || c == '[' || c == '(') stk.push(c);else {//如果是左括號，那么根據當前字符與棧頂元素的ASCII碼值是否小于等于2來判斷是否匹配//匹配的話將當前棧頂去除if(stk.size() && abs(stk.top() - c) <= 2) stk.pop();else return false;}}//如果全部能夠匹配上，那么棧為空return stk.empty();}
};

算法2：枚舉情況：

class Solution {
public:bool isValid(string s) {stack<int> stk;for(auto c : s){if(c == '[' || c == '{' || c == '(') stk.push(c);else{if(stk.size() && c == ']' && stk.top() == '[') stk.pop();else if(stk.size() && c == '}' && stk.top() == '{') stk.pop();else if(stk.size() && c == ')' && stk.top() == '(') stk.pop();else return false;}}return stk.empty();}
};

LeetCode21.合并兩個有序鏈表：

題目描述：

將兩個升序鏈表合并為一個新的升序鏈表并返回。新鏈表是通過拼接給定的兩個鏈表的所有節點組成的。

示例 1：
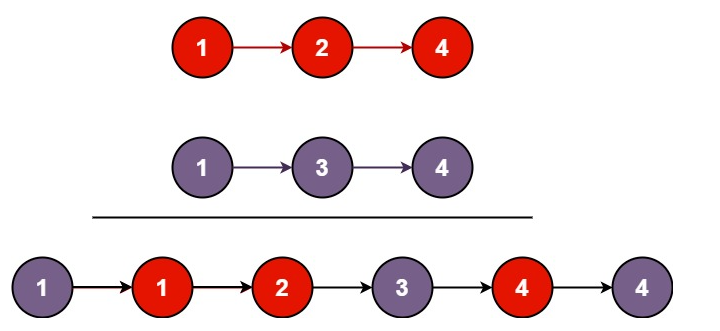
微信圖片_20241104193342.png

輸入：l1 = [1,2,4], l2 = [1,3,4]
輸出：[1,1,2,3,4,4]

示例 2：
輸入：l1 = [], l2 = []
輸出：[]

示例 3：
輸入：l1 = [], l2 = [0]
輸出：[0]

提示：

兩個鏈表的節點數目范圍是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按非遞減順序排列

##注釋代碼：

方法1：

每次將歸并的新鏈表的下一個節點直接指向較小的鏈表節點

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {//定義虛擬頭節點auto dummy = new ListNode(-1);//當前尾節點auto tail = dummy;//每次將最小值歸并到新建鏈表中while(l1 && l2){if(l1 -> val > l2 -> val){tail -> next = l2;tail = tail -> next;l2 = l2 -> next;} else {tail -> next = l1;tail = tail -> next;l1 = l1 -> next;}   }//這里是將l1和l2剩余部分直接拼接到歸并后的鏈表后面，所以不需要指針再一步一步移動if(l1) tail -> next = l1;if(l2) tail -> next = l2;return dummy -> next;}
};

寫法2：

每次將較小的鏈表節點值賦予歸并的新鏈表

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {//定義虛擬頭節點auto dummy = new ListNode(-1);//當前尾節點auto tail = dummy;//每次將最小值歸并到新建鏈表中while(l1 && l2){if(l1 -> val > l2 -> val){tail -> next = new ListNode(l2 -> val);tail = tail -> next;l2 = l2 -> next;} else {tail -> next = new ListNode(l1 -> val);tail = tail -> next;l1 = l1 -> next;}   }//這里是將l1和l2剩余部分直接拼接到歸并后的鏈表后面，所以不需要指針再一步一步移動if(l1) tail -> next = l1;if(l2) tail -> next = l2;return dummy -> next;}
};

純享版：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {auto dummy = new ListNode(-1);auto tail = dummy;while(l1 && l2){if(l1 -> val > l2 -> val){tail -> next = l2;tail = tail -> next;l2 = l2 -> next;}else{tail -> next = l1;tail = tail -> next;l1 = l1 -> next;}}if(l1) tail -> next = l1;if(l2) tail -> next = l2;return dummy -> next;}
};

LeetCode22.括號生成：

題目描述：

數字 n 代表生成括號的對數，請你設計一個函數，用于能夠生成所有可能的并且有效的括號組合。

示例 1：
輸入：n = 3
輸出：[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]

示例 2：
輸入：n = 1
輸出：[“()”]

提示：

1 <= n <= 8

思路：

這里重要的有兩步，一是最后看左右括號數量是否相等，二是每次要看左括號的數量是否大于等于右括號的數量，因為在限制條件下，只要左括號的數量小于右括號，就可以通過添加右括號去合法化方案，但是如果有一個地方右括號數量比左括號多就無法在后面進行補齊

微信截圖_20241104195208.png

代碼：

class Solution {
public:vector<string> res;vector<string> generateParenthesis(int n) {dfs(n, 0, 0, "");return res;}void dfs(int& n, int lc, int rc, string path){if(lc == n && rc == n) res.push_back(path);else{if(rc < n && lc > rc) dfs(n, lc, rc + 1, path + ')');if(lc < n) dfs(n, lc + 1, rc, path + '(');}}
};

LeetCode23.合并K個排序鏈表：

題目描述：

給你一個鏈表數組，每個鏈表都已經按升序排列。

請你將所有鏈表合并到一個升序鏈表中，返回合并后的鏈表。

示例 1：
輸入：lists = [[1,4,5],[1,3,4],[2,6]]
輸出：[1,1,2,3,4,4,5,6]
解釋：鏈表數組如下：
[
1->4->5,
1->3->4,
2->6
]
將它們合并到一個有序鏈表中得到。
1->1->2->3->4->4->5->6

示例 2：
輸入：lists = []
輸出：[]

示例 3：
輸入：lists = [[]]
輸出：[]

提示：

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按升序排列
lists[i].length 的總和不超過 10^4

思路：

跟 LeetCode21.合并兩個有序鏈表一樣，每次將最小的節點值歸并到新的鏈表中，正常做法是枚舉對比每個鏈表的節點值，依次將最小的歸并到新的鏈表中，這樣的話找最小值的時間復雜度是k * n的，但是這里使用優先隊列(小根堆)維護最小值，每次插入和刪除的時間復雜度為log(k)的，那么n個鏈表就是n* log(k)

注意：

這里涉及的優先隊列（默認大根堆）進行重載成小根堆不懂的參考 Acwing839.模擬堆和關于優先隊列大小根堆重載操作符的說明

注釋代碼：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public://對STL容器的比較運算符"()"進行重載//因為STL容器在比較的時候用的是結構體的小括號運算符struct Cmp{//這里一般來說默認是大根堆，默認小的在下面//大根堆的排序判斷是傳入less,也就是比較父子節點的值，如果父節點的值小于子節點那么進行交換//每次將大的值移到上面，所以最后形成大根堆//我們要使用小根堆每次維護最小的節點值，所以要對它的默認判斷進行重載//重載為greater，每次比較父子節點的值，將小的傳到上面，形成小根堆bool operator() (ListNode* a, ListNode* b){return a -> val > b -> val;}};ListNode* mergeKLists(vector<ListNode*>& lists) {priority_queue<ListNode*, vector<ListNode*>, Cmp> heap;auto dummy = new ListNode(-1);auto tail = dummy;//防止傳入空鏈表//這里傳入的是每個鏈表頭節點的地址for(auto l : lists) if(l) heap.push(l);while(heap.size()){//每次取出并去除小根堆的堆頂元素auto t = heap.top();heap.pop();//讓當前新鏈表的尾節點往后移動tail -> next = t;tail = tail -> next;//如果之前堆頂元素的后面還有元素（也就是將堆頂元素所在的鏈表的下一個節點放入到堆中，重新排序，找出最小元素的鏈表的頭節點）if(t -> next) heap.push(t -> next);}return dummy -> next;}
};

純享版：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:struct Cmp{bool operator() (ListNode* a, ListNode* b){return a -> val > b -> val;}};ListNode* mergeKLists(vector<ListNode*>& lists) {priority_queue<ListNode*, vector<ListNode*>, Cmp> h;auto dummy = new ListNode(-1);auto tail = dummy;for(auto l : lists) if(l) h.push(l);while(h.size()){auto temp = h.top();h.pop();tail -> next = temp;tail = tail -> next;if(temp -> next) h.push(temp -> next);}return dummy -> next;}
};

LeetCode24.兩兩交換鏈表中的節點：

題目描述：

給你一個鏈表，兩兩交換其中相鄰的節點，并返回交換后鏈表的頭節點。你必須在不修改節點內部的值的情況下完成本題（即，只能進行節點交換）。

示例 1：
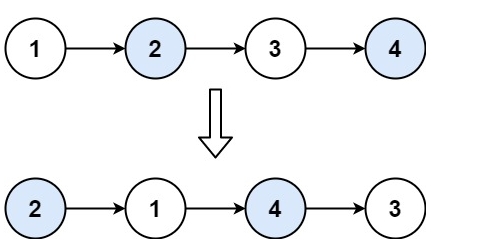
微信截圖_20241105191735.png

輸入：head = [1,2,3,4]
輸出：[2,1,4,3]

示例 2：
輸入：head = []
輸出：[]

示例 3：
輸入：head = [1]
輸出：[1]

提示：

鏈表中節點的數目在范圍 [0, 100] 內
0 <= Node.val <= 100

思路：

鏈表問題慣例定義虛擬頭節點，然后接在鏈表的前面，設立三個指針，維護虛擬頭節點和交換的兩個節點，虛擬頭節點每次移動到要交換的兩個節點前面，只要虛擬頭節點后面兩個節點都存在就進行交換并進行指針移動，這里特別注意的是三個指針之間的移動關系，防止丟失
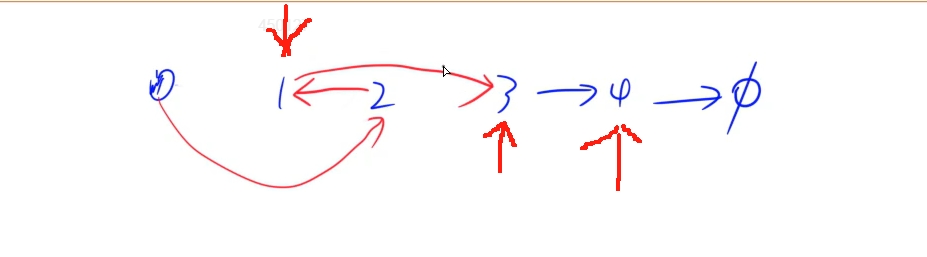
微信截圖_20241105192005.png

代碼：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {auto dummy = new ListNode(-1);dummy -> next = head;for(auto p = dummy; p -> next && p -> next -> next;){auto a = p -> next, b = a -> next;p -> next = b;a -> next = b -> next;b -> next = a;p = a;}return dummy -> next;}
};

純享版：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {auto dummy = new ListNode(-1);dummy -> next = head;auto p = dummy;while(p -> next && p -> next -> next){auto a = p -> next, b = a -> next;a -> next = b -> next;p -> next = b;b -> next = a;p = a;}return dummy -> next;}
};

###LeetCode25.K個一組翻轉鏈表：
##題目描述：

給你鏈表的頭節點 head ，每 k 個節點一組進行翻轉，請你返回修改后的鏈表。

k 是一個正整數，它的值小于或等于鏈表的長度。如果節點總數不是 k 的整數倍，那么請將最后剩余的節點保持原有順序。

你不能只是單純的改變節點內部的值，而是需要實際進行節點交換。

示例 1：

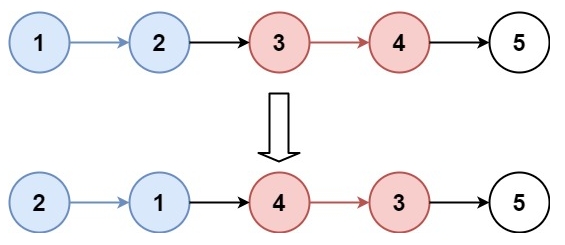
微信截圖_20241105201448.png
輸入：head = [1,2,3,4,5], k = 2
輸出：[2,1,4,3,5]

示例 2：
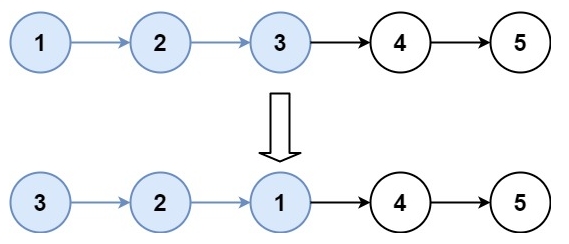
微信截圖_20241105201458.png

輸入：head = [1,2,3,4,5], k = 3
輸出：[3,2,1,4,5]

提示：
鏈表中的節點數目為 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

##思路：題目看起來比較復雜，涉及翻轉又要循環，那么為了將復雜事情簡單化，思路一般為分步：
##第一步：每次循環看當前位置的后面夠不夠k個節點，不足之間跳出
##第二步：對于k個節點內部進行k-1條鏈表邊進行循環翻轉，每兩個點之間翻轉，依次迭代
##第三步：將翻轉后的頭尾重新進行節點銜接

微信圖片編輯_20241105202432.jpg

注意：

處理鏈表問題時，一定要時刻注意存取下一個節點的位置，否則的話無法銜接到正確的位置

注釋代碼：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseKGroup(ListNode* head, int k) {auto dummy = new ListNode(-1);dummy -> next = head;for(auto p = dummy;;){auto q = p;//先判斷p后面夠不夠k個元素： p往后面跳k步后的元素是否為空//保證q不是空節點才往后跳for(int i = 0; i < k && q; i++)  q = q -> next;if(!q) break;//處理內部翻轉//k個節點總共k-1條邊auto a = p -> next, b = a -> next;for(int i = 0; i < k - 1; i++){auto c = b -> next;b -> next = a;  //內部反轉，將后面的指針指向前面//指針錯位（迭代）a = b, b = c;}//每次的頭尾連接auto c = p -> next;p -> next = a;c -> next = b;//將p指針移動到下一次的前一個位置p = c;}return dummy -> next;}
};

純享版：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseKGroup(ListNode* head, int k) {auto dummy = new ListNode(-1);dummy -> next = head;for(auto p = dummy;;){auto temp = p;for(int i = 0; i < k && temp; i++) temp = temp -> next;if(!temp) break;auto a = p -> next, b = a -> next;for(int i = 0; i < k - 1; i++){auto c = b -> next;b -> next = a;a = b, b = c;}auto c = p -> next;p -> next = a;c -> next = b;p = c;}return dummy -> next;}
};

LeetCode26.刪除排序數組中的重復項：

題目描述：

給你一個非嚴格遞增排列的數組 nums ，請你原地刪除重復出現的元素，使每個元素只出現一次，返回刪除后數組的新長度。元素的相對順序應該保持一致。然后返回 nums 中唯一元素的個數。

考慮 nums 的唯一元素的數量為 k ，你需要做以下事情確保你的題解可以被通過：

更改數組 nums ，使 nums 的前 k 個元素包含唯一元素，并按照它們最初在 nums 中出現的順序排列。nums 的其余元素與 nums 的大小不重要。
返回 k 。
判題標準:

系統會用下面的代碼來測試你的題解:

int[] nums = […]; // 輸入數組
int[] expectedNums = […]; // 長度正確的期望答案

int k = removeDuplicates(nums); // 調用

assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有斷言都通過，那么您的題解將被通過。

示例 1：
輸入：nums = [1,1,2]
輸出：2, nums = [1,2,_]
解釋：函數應該返回新的長度 2 ，并且原數組 nums 的前兩個元素被修改為 1, 2 。不需要考慮數組中超出新長度后面的元素。

示例 2：
輸入：nums = [0,0,1,1,1,2,2,3,3,4]
輸出：5, nums = [0,1,2,3,4]
解釋：函數應該返回新的長度 5 ，并且原數組 nums 的前五個元素被修改為 0, 1, 2, 3, 4 。不需要考慮數組中超出新長度后面的元素。

提示：

1 <= nums.length <= 3 * 10^4
-10^4 <= nums[i] <= 10^4
nums 已按非嚴格遞增排列

思路：

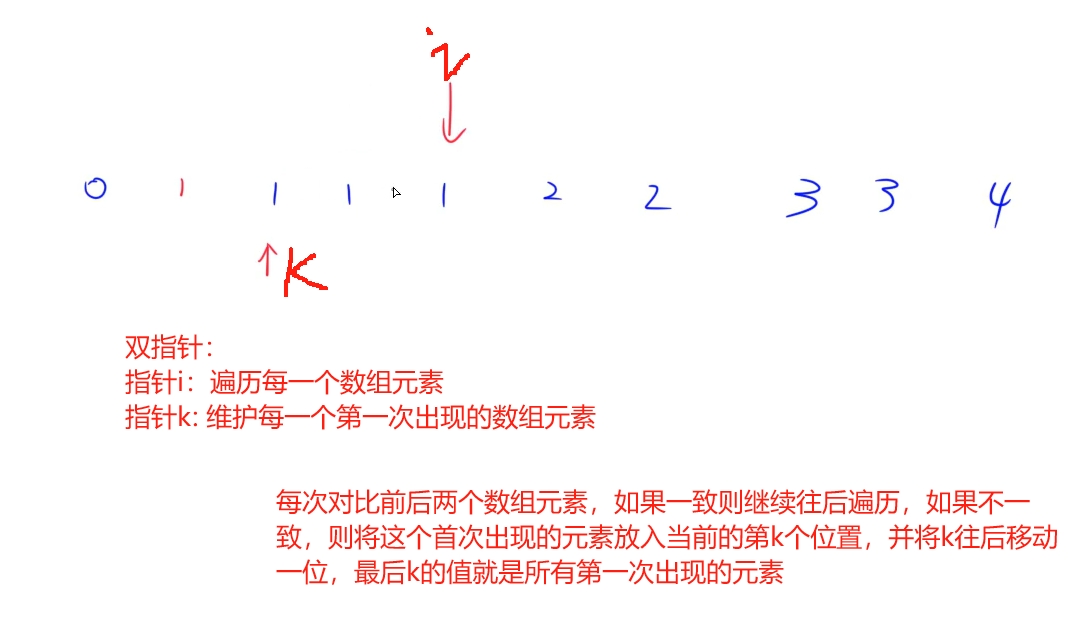
微信截圖_20241105205721.png

代碼：

class Solution {
public:int removeDuplicates(vector<int>& nums) {int k = 0;//k維護每個第一次出現的數組元素for(int i = 0 ; i < nums.size(); i++){//如果i 不為0且當前元素跟上一個元素不一樣if(!i || nums[i] != nums[i - 1]){//將第k個位置替換為當前元素，并且往后移動一位nums[k++] = nums[i];}}//最后k的大小就是數組中第一次出現的所有元素個數return k;}
};

純享版：

class Solution {
public:int removeDuplicates(vector<int>& nums) {int k = 0;for(int i = 0; i < nums.size(); i++){if(!i || nums[i] != nums[i - 1]){nums[k++] = nums[i];}}return k;}
};

LeetCode27.移除元素：

題目描述：

給你一個數組 nums 和一個值 val，你需要原地移除所有數值等于 val 的元素。元素的順序可能發生改變。然后返回 nums 中與 val 不同的元素的數量。

假設 nums 中不等于 val 的元素數量為 k，要通過此題，您需要執行以下操作：

更改 nums 數組，使 nums 的前 k 個元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。
用戶評測：

評測機將使用以下代碼測試您的解決方案：

int[] nums = […]; // 輸入數組
int val = …; // 要移除的值
int[] expectedNums = […]; // 長度正確的預期答案。
// 它以不等于 val 的值排序。

int k = removeElement(nums, val); // 調用你的實現

assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 個元素
for (int i = 0; i < actualLength; i++) {
assert nums[i] == expectedNums[i];
}
如果所有的斷言都通過，你的解決方案將會通過。

示例 1：
輸入：nums = [3,2,2,3], val = 3
輸出：2, nums = [2,2,,]
解釋：你的函數函數應該返回 k = 2, 并且 nums 中的前兩個元素均為 2。
你在返回的 k 個元素之外留下了什么并不重要（因此它們并不計入評測）。

示例 2：
輸入：nums = [0,1,2,2,3,0,4,2], val = 2
輸出：5, nums = [0,1,4,0,3,,,_]
解釋：你的函數應該返回 k = 5，并且 nums 中的前五個元素為 0,0,1,3,4。
注意這五個元素可以任意順序返回。
你在返回的 k 個元素之外留下了什么并不重要（因此它們并不計入評測）。

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

思路：

跟 LeetCode26.刪除有序數組中的重復項思路一樣

代碼：

class Solution {
public:int removeElement(vector<int>& nums, int val) {int k = 0; for(int i = 0; i < nums.size(); i++){if(nums[i] != val){nums[k++] = nums[i];}}return k;}
};

LeetCode28.實現strStr():

題目描述：

給你兩個字符串 haystack 和 needle ，請你在 haystack 字符串中找出 needle 字符串的第一個匹配項的下標（下標從 0 開始）。如果 needle 不是 haystack 的一部分，則返回 -1 。

示例 1：
輸入：haystack = “sadbutsad”, needle = “sad”
輸出：0
解釋：“sad” 在下標 0 和 6 處匹配。
第一個匹配項的下標是 0 ，所以返回 0 。

示例 2：
輸入：haystack = “leetcode”, needle = “leeto”
輸出：-1
解釋：“leeto” 沒有在 “leetcode” 中出現，所以返回 -1 。

提示：

1 <= haystack.length, needle.length <= 10^4
haystack 和 needle 僅由小寫英文字符組成

算法1：

思路：暴力枚舉O(NM)

直接按照定義，從長串的每一個字符開始暴力匹配子串
##時間復雜度：兩重循環，O(nm)

class Solution {
public:int strStr(string s, string p) {int n = s.size(), m = p.size();for(int i = 0; i < n - m + 1; i++){bool st = true;for(int j = 0; j < m; j++){if(s[i + j] != p[j]){st = false;break;}}if(st) return i;}return -1;}
};

算法2：

思路：

創建子串的next數組，當前匹配不上時，下一個可以直接開始比較的位置（前綴和后綴相等的最大長度）
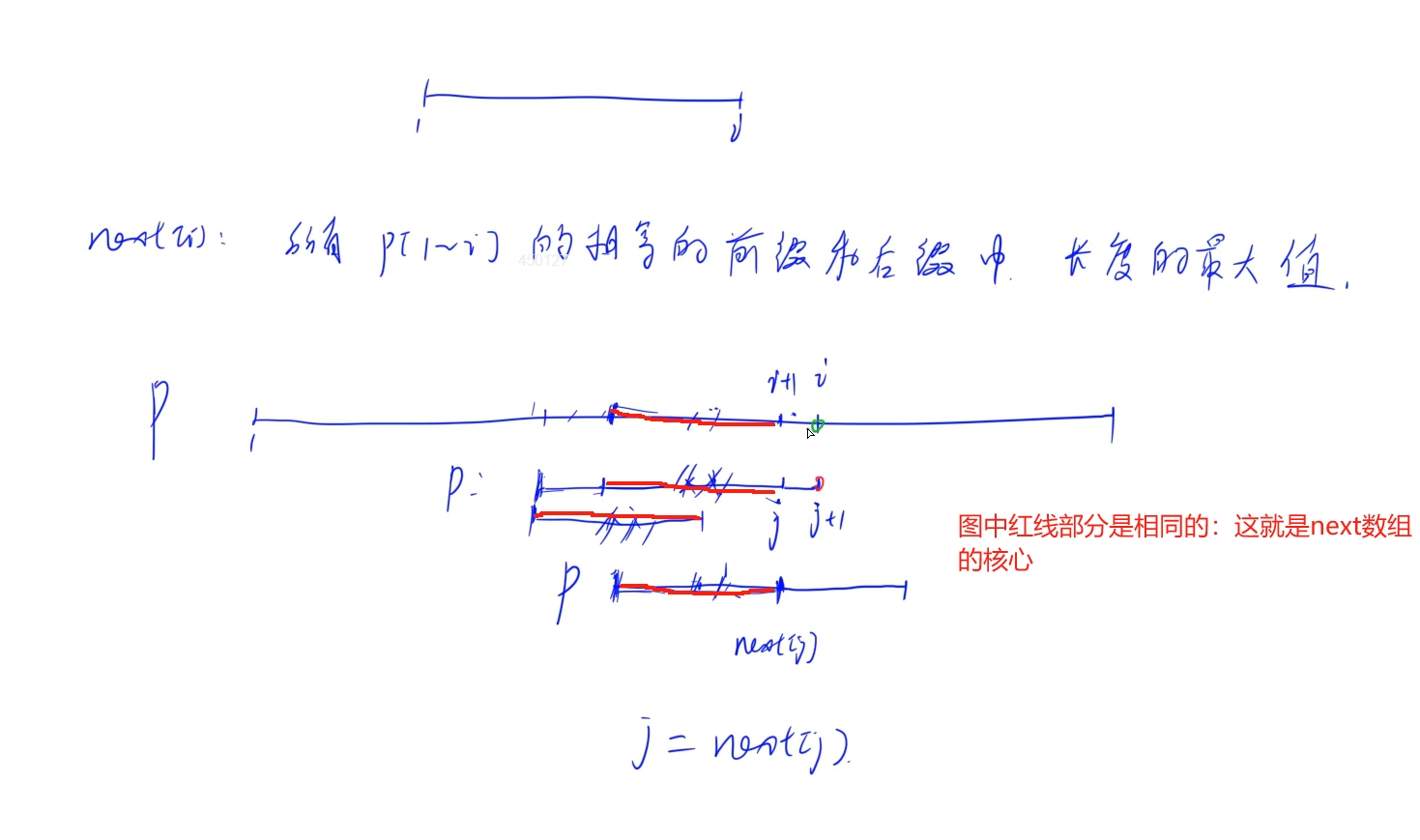
微信截圖_20241106210647.png

KMP：

時間復雜度： O(n + m)

class Solution {
public:int strStr(string s, string p) {if(p.empty()) return 0;int n = s.size(), m = p.size();s = ' ' + s, p = ' ' + p;vector<int> next(m + 1);//求next數組//其實是自身進行匹配的過程//一直循環往復for(int i = 2, j = 0; i <= m; i++){while(j && p[i] != p[j + 1]) j = next[j];//如果此時j的后面一位（前綴：j + 1）跟它原本相同的后綴的后面一位相同，說明此時可以擴展一位if(p[i] == p[j + 1]) j++;//將最長的前綴和后綴長度放入next數組next[i] = j;}//KMP匹配過程for(int i = 1, j = 0; i <= n; i++){//如果不匹配了， 將j跳轉到next[j]的位置//也就是p[1~j]中前綴和后綴相同的最大長度的位置，節省前面next[j]個字符的匹配//或者是j退無可退的情況下，從頭開始匹配while(j && s[i] != p[j + 1]) j = next[j];//當后面的一個字符能繼續匹配，j往后移動if(s[i] == p[j + 1]) j++;//如果能完全匹配 m個字符，那么返回第一個匹配字符的下標//這里 返回i- m 是因為原本是 i - m + 1, 但是由于把字符串增加了一位，所以變成i -mif(j == m) return i - m;}return -1;}
};

純享版：

class Solution {
public:int strStr(string s, string p) {int n = s.size(), m = p.size();if(m == 0) return 0;s = ' ' + s, p = ' ' + p;vector<int> next(m + 1);for(int i = 2, j = 0; i <=  m; i++){while(j && p[i] != p[j + 1]) j = next[j];if(p[i] == p[j + 1]) j++;next[i] = j;}for(int i = 1, j = 0; i <= n; i++){while(j && s[i] != p[j + 1]) j = next[j];if(s[i] == p[j + 1]) j++;if(j == m) return i - m;}return -1;}
};

LeetCode29.兩數相除：

題目描述：

給你兩個整數，被除數 dividend 和除數 divisor。將兩數相除，要求不使用乘法、除法和取余運算。

整數除法應該向零截斷，也就是截去（truncate）其小數部分。例如，8.345 將被截斷為 8 ，-2.7335 將被截斷至 -2 。

返回被除數 dividend 除以除數 divisor 得到的商。

注意：假設我們的環境只能存儲 32 位有符號整數，其數值范圍是 [?2^31, 2^31 ? 1] 。本題中，如果商嚴格大于 2^31 ? 1 ，則返回 2^31 ? 1 ；如果商嚴格小于 -2^31 ，則返回 -2^31 。

示例 1:
輸入: dividend = 10, divisor = 3
輸出: 3
解釋: 10/3 = 3.33333… ，向零截斷后得到 3 。

示例 2:
輸入: dividend = 7, divisor = -3
輸出: -2
解釋: 7/-3 = -2.33333… ，向零截斷后得到 -2 。

提示：

-2^31 <= dividend, divisor <= 2^31 - 1
divisor != 0

思路：

正常暴力做的話就是每次被除數減去除數，但是當被除數為2^31 -1，除數為1時，需要執行2^{31-1(大約10}19)次，肯定超時,所以這里使用類似于快速冪的思想，將商轉換成二進制表示，從高往低判斷商的當前位是否為1，如果為1就減去當前位，繼續判斷，這樣只要減不超過30次，就能很快確定商的值

注釋代碼：

class Solution {
public:int divide(int x, int y) {typedef long long LL;//exp存指數項vector<LL> exp;//確定符號， false 表示結果是正數bool is_minus = false;//如果x, y符號不相同，那么，令符號標記為trueif(x < 0 && y > 0 || x > 0 && y < 0) is_minus = true;//取 x, y 的絕對值，方便計算LL a = abs((LL)x), b = abs((LL) y);//將b的指數項依次存入exp中for(LL i = b; i <= a; i = i + i) exp.push_back(i);LL res = 0;for(int i = exp.size() - 1; i >= 0; i--){if(a >= exp[i]){//說明商的當前位上應該是1a -= exp[i];//答案加上當前商res += 1ll << i;}}//最后加上符號if(is_minus)  res = -res;if(res > INT_MAX ||res < INT_MIN) return INT_MAX;return res;}
};

純享版：

class Solution {
public:int divide(int x, int y) {typedef long long LL;vector<LL> exp;bool is_minus = false;if(x > 0 && y < 0 || x < 0 && y > 0) is_minus = true;LL a = abs((LL)x), b = abs((LL)y);for(LL i = b; i <= a; i = i + i)  exp.push_back(i);LL res = 0;for(int i = exp.size() - 1; i >= 0; i--){if(a >= exp[i]){a -= exp[i];res += 1ll << i;}}if(is_minus) res = -res;if(res > INT_MAX || res < INT_MIN) return INT_MAX;return res;}
};

LeetCode30.串聯所有單詞的子串：

題目描述：

給定一個字符串 s 和一個字符串數組 words。 words 中所有字符串長度相同。
s 中的串聯子串是指一個包含 words 中所有字符串以任意順序排列連接起來的子串。

例如，如果 words = [“ab”,“cd”,“ef”]，那么 “abcdef”， “abefcd”，“cdabef”， “cdefab”，“efabcd”，和 “efcdab” 都是串聯子串。 “acdbef” 不是串聯子串，因為他不是任何 words 排列的連接。
返回所有串聯子串在 s 中的開始索引。你可以以任意順序返回答案。

示例 1：

輸入：s = “barfoothefoobarman”, words = [“foo”,“bar”]
輸出：[0,9]
解釋：因為 words.length == 2 同時 words[i].length == 3，連接的子字符串的長度必須為 6。
子串 “barfoo” 開始位置是 0。它是 words 中以 [“bar”,“foo”] 順序排列的連接。
子串 “foobar” 開始位置是 9。它是 words 中以 [“foo”,“bar”] 順序排列的連接。
輸出順序無關緊要。返回 [9,0] 也是可以的。

示例 2：

輸入：s = “wordgoodgoodgoodbestword”, words = [“word”,“good”,“best”,“word”]
輸出：[]
解釋：因為 words.length == 4 并且 words[i].length == 4，所以串聯子串的長度必須為 16。
s 中沒有子串長度為 16 并且等于 words 的任何順序排列的連接。
所以我們返回一個空數組。
示例 3：

輸入：s = “barfoofoobarthefoobarman”, words = [“bar”,“foo”,“the”]
輸出：[6,9,12]
解釋：因為 words.length == 3 并且 words[i].length == 3，所以串聯子串的長度必須為 9。
子串 “foobarthe” 開始位置是 6。它是 words 中以 [“foo”,“bar”,“the”] 順序排列的連接。
子串 “barthefoo” 開始位置是 9。它是 words 中以 [“bar”,“the”,“foo”] 順序排列的連接。
子串 “thefoobar” 開始位置是 12。它是 words 中以 [“the”,“foo”,“bar”] 順序排列的連接。

提示：

1 <= s.length <= 10^4
1 <= words.length <= 5000
1 <= words[i].length <= 30
words[i] 和 s 由小寫英文字母組成

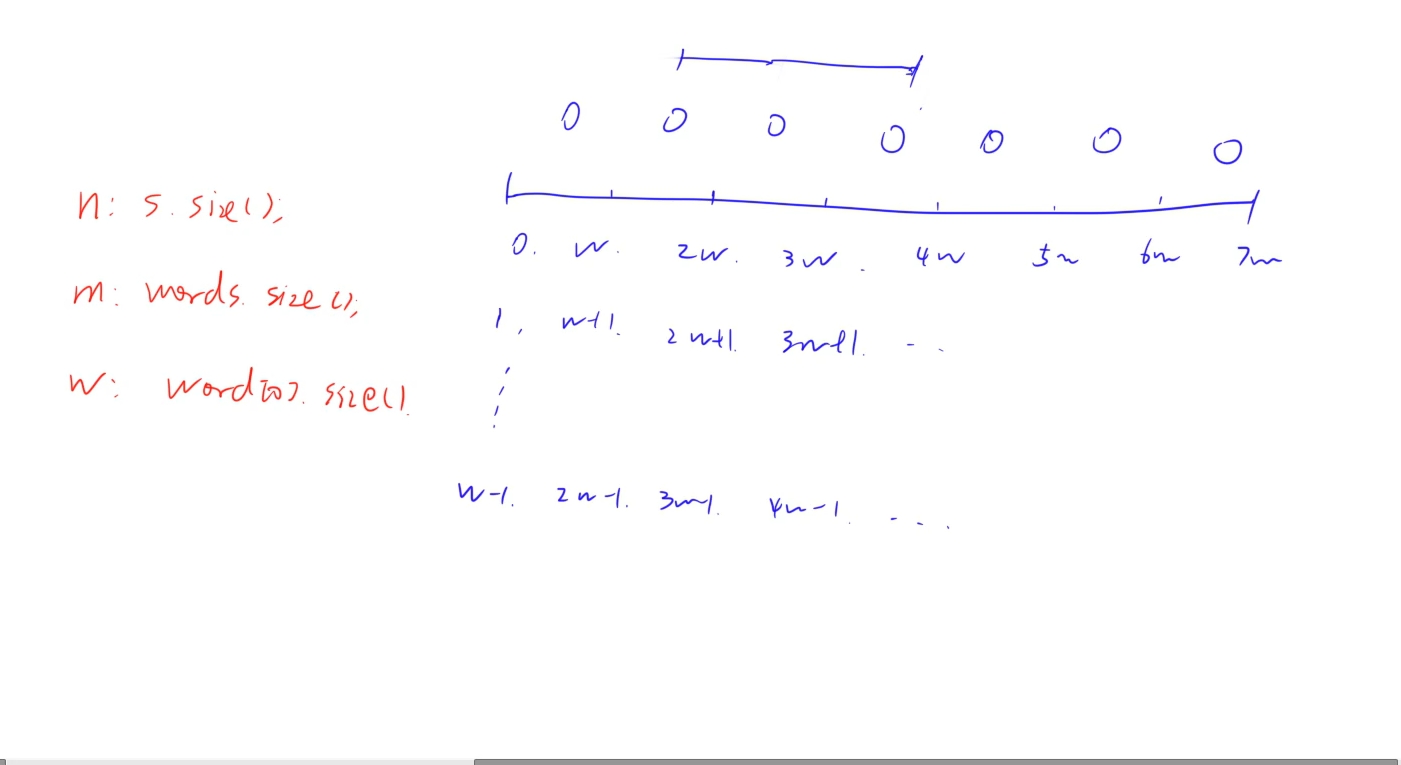
思路：

這里的思路是將s字符串按照words的單詞長度w進行區間劃分，從0 ~ w-1為起止位置，每次劃分w的長度，這樣做相當于每一個槽位剛好是單個單詞，可以直接將s字符串的所有單詞通過巧妙的方式列舉出來，然后對于words的單詞匹配則使用滑動窗口進行匹配，同時使用cnt記錄有效單詞的個數，這里的cnt主要作用是記錄在當前窗口維護的有效單詞，如果有效單詞個數等于words單詞個數，那么說明這是一種匹配方案

注意：

這里的cnt是有效單詞的個數，進入滑動窗口時會根據窗口中的次數跟tot中words單詞出現的次數進行判斷

微信截圖_20241107212437.png

注釋代碼：

class Solution {
public:vector<int> findSubstring(string s, vector<string>& words) {vector<int>res;if(words.empty()) return res;int n = s.size(), m = words.size(), w = words[0].size();//單詞池的每個單詞出現的次數unordered_map<string, int> tot;//將每個單詞對應出現的次數+1for(auto&word : words) tot[word]++;//從0 ~w-1 開始按w固定長度劃分整個區間for(int i = 0; i < w; i++){//當前窗口維護的單詞unordered_map<string, int> wd;//cnt : 確定有多少個單詞是給定tot集合中的//cnt 維護的是有效的單詞，如果沒有在tot集合中出現過，或者出現次數大于tot集合次數都是被排除在外的   int cnt = 0;//將整個字符串按固定長度w劃分，起始位置從0 ~ w，每次一個槽位剛好對應一個單詞for(int j = i; j + w <= n; j += w){//窗口大小滿足m個單詞的話if(j >= i + m * w){//將最前面放入的單詞找出來auto word = s.substr(j - m * w, w);//每次窗口移動到刪除最前面放入的單詞wd[word]--;//如果刪除該單詞之后，小于tot中對應出現的次數//說明刪除的是有效單詞，從cnt中減去一個有效單詞//這里的wd無論出現哪個單詞，對應出現的次數都是1，最壞的情況都是1//但是，對于tot來說，如果不是有效的單詞，那么它出現的次數為0//所以這里只要刪除當前單詞使得wd的次數小于tot中的次數了，說明刪除的是一個有效單詞if(wd[word] < tot[word]) cnt--;}//通過槽位找到下一個單詞auto word = s.substr(j, w);//將該單詞加入到到當前窗口wd[word]++;//如果該單詞加入之后，滿足tot中應該出現的次數，說明是有效單詞if(wd[word] <= tot[word]) cnt++;//通過這種方式，每次將有效單詞計入cnt，當cnt == words中的單詞數量，說明能夠匹配到相同的字符串//將當前的起始位置存入答案if(cnt == m) res.push_back(j - (m -1) * w);}}return res;}
};

純享版：

class Solution {
public:vector<int> findSubstring(string s, vector<string>& words) {vector<int> res;if(words.empty()) return res;int n = s.size(), m = words.size(), w = words[0].size();unordered_map<string, int> tot;for(auto word : words) tot[word]++;for(int i = 0; i < w; i++){unordered_map<string, int> wd;int cnt = 0;for(int j = i; j + w <= n; j += w){if(j >= i + m * w){auto word = s.substr(j - m * w,w);wd[word]--;if(wd[word] < tot[word]) cnt--;}auto word = s.substr(j, w);wd[word]++;if(wd[word] <= tot[word]) cnt++;if(cnt == m) res.push_back(j - (m - 1) * w);}}return res;}
};