在上篇文章中我們主要講了關于實現二叉樹的內容,包括遍歷二叉樹,以及統計二叉樹等內容。而
在這篇文章中我們將詳細講解一下利用隊列的知識實現層序遍歷二叉樹。
那么層序遍歷是什么?以及利用隊列遍歷二叉樹又是怎么遍歷的?下面讓我們一起帶著這些問題深
入研究:
1. 什么是層序遍歷?
我們仍然以之前使用過的二叉樹為例。
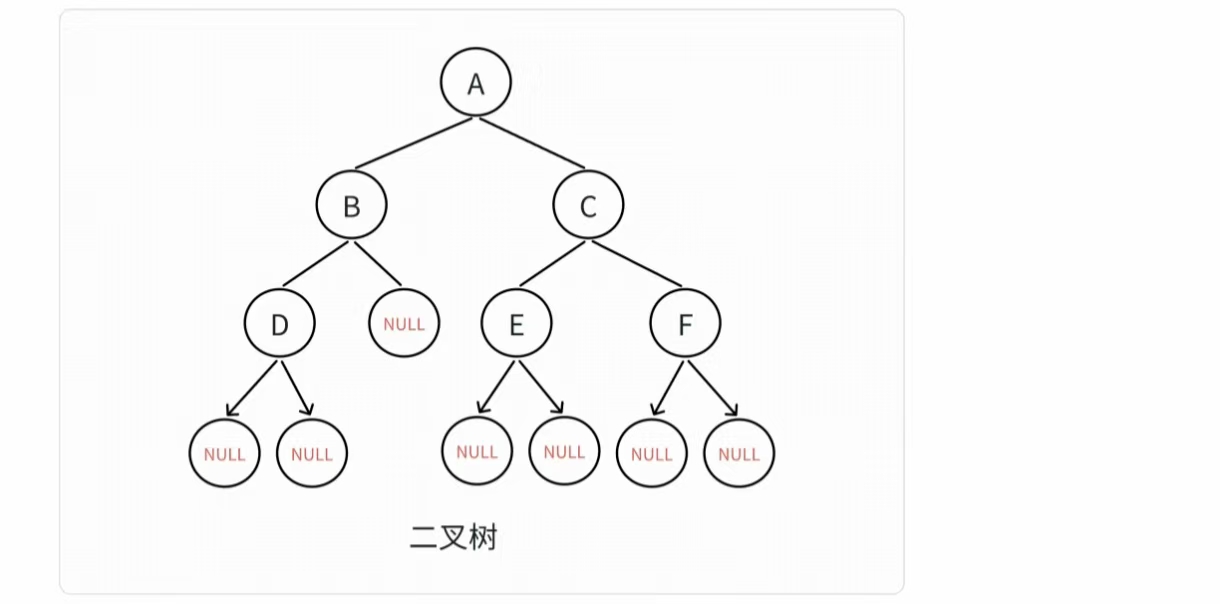
對于二叉樹而言 : 層序遍歷二叉樹,簡單說就是按“層次”訪問節點:從根節點開始,先訪問第1層
(根),再訪問第2層(根的左右孩子),接著第3層……逐層從左到右訪問每個節點,直到所有節
點都被訪問。所以對于這棵二叉樹而言,我們可以簡單的推論出這棵二叉樹的層序遍歷就是 :?A? B
C? D? NULL? E? F? NULL? NULL? NULL? NULL? NULL? NULL
2. 為什么要使用隊列實現層序遍歷二叉樹?
用隊列實現這棵二叉樹的層序遍歷,核心就是利用了隊列“先進先出”的特性,剛好匹配層序遍歷
“一層一層、從左到右”的需求。
3.怎樣使用隊列實現層序遍歷二叉樹呢?
利用隊列實現二叉樹層序遍歷,核心是用隊列存儲節點和借助隊列 “先進先出” 的特性,讓二叉樹
節點按 “一層一層、從左到右” 的順序被訪問,具體邏輯可拆解為 3 步:
1. 核心原理:隊列如何適配層序需求
二叉樹層序遍歷要 “按層訪問”,但二叉樹節點靠指針(?left?/?right?)關聯,本身無 “層” 的顯式順
序。隊列的 “先進先出” 特性,能把二叉樹的 “層次順序” 轉化為隊列的 “線性順序”:
- 處理當前層節點時,把下一層節點(左右子節點)按順序入隊 → 保證下一層節點會 “排隊等
待”,按入隊順序被處理(契合層序 “從左到右、一層一層” 的規則)。
2. 隊列的 “先進先出” 完美匹配層序遍歷需求:
- “先進”:處理當前層節點時,優先把下一層的左子節點入隊(保證層序 “從左到右”)。
- “先出”:隊列頭部始終是 “當前層最早入隊的節點”,處理完彈出 → 保證層序 “一層一層” 推進。
對比其他結構(如棧):若用棧(后進先出),節點處理順序會混亂,無法實現 “按層訪問”。因
此,隊列是層序遍歷的 “最佳搭檔”,用其特性彌補了二叉樹層次順序的隱式問題。
簡單說,隊列是層序遍歷的 “工具”:用它的 “排隊邏輯”,把二叉樹的層次關系轉化為可順序處理的
線性結構,讓層序遍歷從抽象需求落地成代碼邏輯?。
4. 代碼的實現
層序遍歷函數(?levelOrder?):
void levelOrder(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){//取隊頭,出對頭BTNode* top = QueueFront(&q);QueuePop(&q);printf("%c ", top->data);//將對頭非空左右孩子入隊列if (top->left){QueuePush(&q, top->left);}if (top->right){QueuePush(&q, top->right);}}QueueDestroy(&q);
}以下從層序遍歷邏輯和隊列與二叉樹的關系兩方面詳細講解:
層序遍歷核心是按“一層一層”的順序訪問二叉樹節點,借助隊列實現,步驟如下:
1.?初始化隊列
Queue q;
QueueInit(&q);
QueuePush(&q, root);?- 先創建隊列 ?q??并初始化,再把二叉樹根節點?root?入隊。此時隊列里只有根節點,是層序遍歷的
起點。
2.?循環處理隊列(核心邏輯)
while (!QueueEmpty(&q))?
{BTNode* top = QueueFront(&q); // 取隊頭(當前層節點)QueuePop(&q); ? ? ? ? ? ? ? ? // 彈出隊頭(處理完當前節點,出隊)printf("%c ", top->data); ? ? // 訪問節點數據(打印,也可做其他操作)// 非空左右孩子入隊(為下一層遍歷做準備)if (top->left) ?QueuePush(&q, top->left); ?if (top->right) QueuePush(&q, top->right);?
}
- 循環條件:隊列非空時,持續處理節點(隊列空說明所有層遍歷完畢)。
- 取節點 & 出隊:?QueueFront??拿到當前層的節點(隊頭),?QueuePop??把它移出隊列(因為要
處理該節點的邏輯了)。
- 訪問節點:通過 ?top->data??訪問當前節點數據(比如打印)。
- 子節點入隊:若當前節點的左、右孩子非空,依次入隊——這是層序遍歷的關鍵!保證下一層節
點按順序排隊,后續循環會按“先入先出”處理,自然實現“一層一層”遍歷。
3. 隊列與二叉樹的關系
層序遍歷中,隊列是“橋梁”,用“先入先出”特性適配二叉樹“一層一層訪問”的需求,具體關系體現
在:
1.?隊列的作用:“暫存 + 順序控制”
- 暫存節點:遍歷某一層時,把當前層節點的非空左右孩子入隊,這些孩子屬于“下一層節點”。
- 順序控制:隊列保證節點“先進先出”,契合層序遍歷“從左到右、一層一層”的順序。比如根節點先
入隊,處理根節點時,左、右孩子入隊;后續先處理左孩子(隊頭),再處理右孩子(隊列里排隊
的),完美匹配層序遍歷邏輯。
2.?二叉樹結構對隊列的依賴
二叉樹節點是“分散”的(通過指針關聯左右孩子),無法直接按“層”遍歷。隊列通過“入隊(記錄
下一層節點)→ 出隊(處理當前層節點)”的流程,把二叉樹“分層”的邏輯,轉化為隊列的“線性順
序”操作,讓層序遍歷可實現。
4. 總結:
層序遍歷函數用隊列實現“分層訪問”,隊列的“先入先出”特性,完美匹配二叉樹“一層一層遍歷”的需
求:
- 隊列暫存“下一層節點”,保證遍歷順序;
- 二叉樹的“分層邏輯”,通過隊列轉化為簡單的“入隊 → 出隊 → 處理”流程
4. 函數中用到的隊列相關函數及其作用
假設隊列的底層實現為“鏈式隊列”,以下是各函數的功能說明:
1.??QueueInit(&q)?
- 作用:初始化隊列 ?q?,通常包括設置隊頭/隊尾指針為 ?NULL?、初始化節點數量等,確保隊列可
正常使用。
2.??QueuePush(&q, root)?
- 作用:將節點 ?root??插入隊列尾部(入隊操作),保持“先進先出”的順序。
- 層序遍歷中,用于將當前節點的左右子節點加入隊列,作為下一層的待處理節點。
3.??QueueEmpty(&q)?
- 作用:判斷隊列是否為空(返回 ?true??或 ?false?)。
- 作為循環終止條件:當隊列為空時,說明所有節點已遍歷完畢。
4.??QueueFront(&q)?
- 作用:獲取隊列的隊頭節點(不刪除節點),返回節點指針。
- 層序遍歷中,用于獲取當前層的待訪問節點。
5.??QueuePop(&q)?
- 作用:刪除隊列的隊頭節點(出隊操作)。
- 層序遍歷中,處理完隊頭節點后將其移除,避免重復訪問。
6.??QueueDestroy(&q)?
- 作用:銷毀隊列,釋放隊列占用的所有內存(包括所有節點)。
- 必須在遍歷結束后調用(原代碼放在循環內是錯誤的,會導致第一次循環后隊列被銷毀,后續操
作失敗)。
注意 : 上面關于隊列的函數小編均在之前的文章中都有講過。想深入了解的小伙伴可以去看一看。
并且上面的代碼都是基于隊列和二叉樹的代碼基礎上實現。
5. 總結:
levelOrder??函數通過隊列實現二叉樹層序遍歷,核心總結如下:
1.?初始化隊列并將根節點入隊,作為遍歷起點;
2.?循環處理隊列(隊列非空時):
- 取出隊頭節點,訪問其數據(打印);
- 將該節點的非空左右子節點依次入隊(為下一層遍歷做準備);
3.?遍歷結束后銷毀隊列
簡言之,隊列的“先進先出”特性保證了節點按“一層一層、從左到右”的順序被訪問,是層序遍歷的
關鍵工具。
以上便是關于隊列實現層序遍歷二叉樹的全部內容。最后感謝大家的觀看!
)

對北半球光伏數據進行時間序列預測)
















