dfs二叉樹中的深搜(回溯、剪枝)--力扣129、814、230、257

1.1題目鏈接：129.求根節點到葉結點數字之和

1.2題目描述：給你一個二叉樹的根節點?root?，樹中每個節點都存放有一個?0?到?9?之間的數字。

1.3解法(dfs-前序遍歷)：

2.1題目鏈接：814.二叉樹剪枝

2.2題目描述：

2.3解法(dfs-后序遍歷)：

3.1題目鏈接：98.驗證二叉搜索樹

3.2題目描述：

3.3解法(利用中序遍歷)

4.1題目鏈接：230.二叉搜索樹中第K小的元素

4.2題目描述：

4.3解法(中序遍歷+計數器剪枝)

5.1題目鏈接：257.二叉樹的所有路徑

5.2題目描述：

5.3解法(回溯)：

本文提供了四道關于二叉樹的問題及它們的解法：

求根節點到葉結點數字之和：給定一個二叉樹，樹中每個節點存放一個0到9之間的數字，求從根節點到葉節點生成的所有數字之和。解法使用深度優先搜索（DFS）的前序遍歷，整合父節點信息與當前節點信息計算當前節點數字，并遞歸向下傳遞，在葉子節點處返回結果。
二叉樹剪枝：給定一個二叉樹，節點值為0或1，返回移除所有不包含1的子樹的原二叉樹。解法使用DFS的后序遍歷，逐步刪除葉子節點，保證刪除后節點仍滿足條件。
驗證二叉搜索樹：判斷給定二叉樹是否是有效的二叉搜索樹。解法利用中序遍歷，遞歸判斷左子樹是否為BST，當前節點是否滿足BST條件，以及右子樹是否為BST。
二叉搜索樹中第K小的元素：在二叉搜索樹中查找第K小的元素。解法使用中序遍歷配合計數器進行剪枝，當計數器等于0時找到第K小的元素。

此外，還提供了第5道題目二叉樹的所有路徑，返回所有從根節點到葉子節點的路徑的解法，使用回溯法將路徑存儲在結果中。

1.1題目鏈接：129.求根節點到葉結點數字之和

1.2題目描述：
給你一個二叉樹的根節點?`root`?，樹中每個節點都存放有一個?`0`?到?`9`?之間的數字。

每條從根節點到葉節點的路徑都代表一個數字：

例如，從根節點到葉節點的路徑?1 -> 2 -> 3?表示數字?123?。

計算從根節點到葉節點生成的?所有數字之和?。

葉節點?是指沒有子節點的節點。

示例 1：

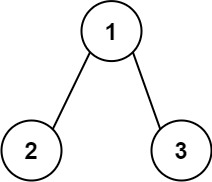
輸入：root = [1,2,3]
輸出：25
解釋：
從根到葉子節點路徑 1->2 代表數字 12
從根到葉子節點路徑 1->3 代表數字 13
因此，數字總和 = 12 + 13 = 25

示例 2：

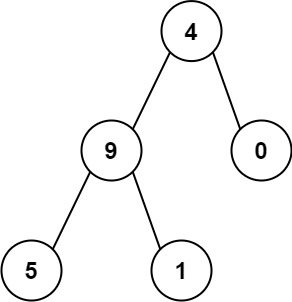
輸入：root = [4,9,0,5,1]
輸出：1026
解釋：
從根到葉子節點路徑 4->9->5 代表數字 495
從根到葉子節點路徑 4->9->1 代表數字 491
從根到葉子節點路徑 4->0 代表數字 40
因此，數字總和 = 495 + 491 + 40 = 1026

提示：

樹中節點的數目在范圍?[1, 1000]?內
0 <= Node.val <= 9
樹的深度不超過?10

1.3解法(dfs-前序遍歷)：

前序遍歷按照根結點、左子樹、右子樹的順序遍歷二叉樹的所有結點，通常用于子節點的狀態依賴于父節點狀態的題目。

算法思路：

在前序遍歷的過程中，我們可以往左右子樹傳遞信息，并且在回溯時得到左右子樹的返回值。遞歸函數可以幫我們完成兩件事：

將父節點的數字與當前結點的信息整合到一起，計算出當前結點的數字，然后傳遞到下一層進行遞歸；
當遇到葉子結點的時候，就不再向下傳遞信息，而是將整合的結果向上一直回溯到根節點。

當遞歸結束時，根結點需要返回的值也就被更新為了整棵數的數字和。

算法流程：
遞歸函數設計：int dfs(TreeNode* root, int num)

返回值：當前子樹計算的結果(數字和)；
參數num：遞歸過程中往下傳遞的信息(父結點的數字)
函數作用：整合父節點的信息與當前結點的信息計算當前結點數字，并向下傳遞，在回溯時返回當前子樹(當前結點作為子樹根結點)數字和

遞歸函數流程：

當遇到空節點的時候，說明這條路從根節點開始沒有分支，返回0
結合父節點傳下的信息以及當前節點的val，計算出當前節點數字sum
如果當前節點是葉子節點，直接返回整合后的結果sum
如果當前節點不是葉子節點，將sum傳到左右子樹中去，得到左右子樹中節點路徑的數字和，然后相加返回結果。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumNumbers(TreeNode* root) {return dfs(root,0);}int dfs(TreeNode* root, int sum){sum = sum*10 + root->val;if(root->left == nullptr && root->right == nullptr){return sum;}int ret = 0;if(root->left)ret += dfs(root->left, sum);if(root->right)ret += dfs(root->right, sum);return ret;}
};

2.1題目鏈接：814.二叉樹剪枝

2.2題目描述：

給你二叉樹的根結點?root?，此外樹的每個結點的值要么是?0?，要么是?1?。

返回移除了所有不包含?1?的子樹的原二叉樹。

節點?node?的子樹為?node?本身加上所有?node?的后代。

示例 1：

輸入：root = [1,null,0,0,1]
輸出：[1,null,0,null,1]
解釋：
只有紅色節點滿足條件“所有不包含 1 的子樹”。 右圖為返回的答案。

示例 2：

輸入：root = [1,0,1,0,0,0,1]
輸出：[1,null,1,null,1]

示例 3：

輸入：root = [1,1,0,1,1,0,1,0]
輸出：[1,1,0,1,1,null,1]

提示：

樹中節點的數目在范圍?[1, 200]?內
Node.val?為?0?或?1

2.3解法(dfs-后序遍歷)：

后序遍歷按照左子樹、右子樹、根節點的順序遍歷二叉樹的所有結點，通常用于父節點的狀態依賴于子結點狀態的題目。

算法思路：

如果我們選擇從上往下刪除，我們需要收集左右子樹的信息，這可能導致代碼編寫相對困難。然而，通過觀察我們可以發現，如果我們先刪除最底部的葉子結點，然后再處理刪除后的結點，最終的結果并不會受到影響。

因此，我們可以采用后序遍歷的方式來解決這個問題。在后序遍歷中，我們先處理左子樹，然后處理右子樹，最后再處理當前節點。在處理當前節點時，我們可以判斷其是否為葉子節點且其值是否為0，如果滿足條件，我們可以刪除當前節點。

需要注意的是，在刪除葉子節點時，其父節點很可能會成為新的葉子節點。因此，在處理完子節點后，我們仍然需要處理當前節點。這也是為什么選擇后序遍歷的原因（后序遍歷首先遍歷到的一定是葉子節點）。
通過使用后序遍歷，我們可以逐步刪除葉子節點，并且保證刪除后的節點仍然滿足刪除操作的要求。這樣，我們可以較為方便地實現刪除操作，而不會影響最終的結果。
若在處理結束后所有葉子節點的值均為1，則所有子樹均包含1，此時可以返回。

算法流程：

遞歸函數設計：void dfs(TreeNode* root)

返回值：無；
參數：當前需要處理的節點
函數作用：判斷當前節點是否需要刪除，若需要刪除，則刪除當前節點。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root == nullptr) return nullptr;root->left = pruneTree(root->left);root->right = pruneTree(root->right);if(root->left == nullptr && root->right == nullptr && root->val == 0){delete root;//防止內存泄漏root = nullptr;}return root;}
};

3.1題目鏈接：98.驗證二叉搜索樹

3.2題目描述：

給你一個二叉樹的根節點?root?，判斷其是否是一個有效的二叉搜索樹。

有效?二叉搜索樹定義如下：

節點的左子樹只包含?小于?當前節點的數。
節點的右子樹只包含?大于?當前節點的數。
所有左子樹和右子樹自身必須也是二叉搜索樹。

示例 1：

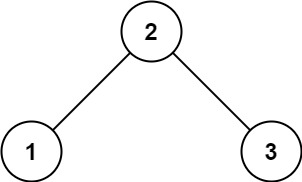
輸入：root = [2,1,3]
輸出：true

示例 2：

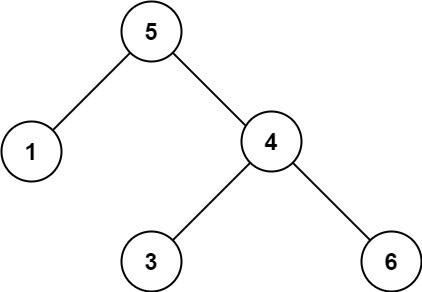
輸入：root = [5,1,4,null,null,3,6]
輸出：false
解釋：根節點的值是 5 ，但是右子節點的值是 4 。

提示：

樹中節點數目范圍在[1, 10^4]?內
-2^31 <= Node.val <= 2^31 - 1

3.3解法(利用中序遍歷)

后序遍歷按照左子樹、根節點、右子樹的順序遍歷二叉樹的所有節點，通常用于二叉搜索樹相關題目。
算法思路：
如果一棵樹是二叉搜索樹，那么它的中序遍歷的結果一定是一個嚴格遞增的序列。
因此，我們可以初始化一個無窮小的全區變量，用來記錄中序遍歷過程中的前驅結點。那么就可以在中序遍歷的過程中，先判斷是否和前驅結點構成遞增序列，然后修改前驅結點為當前結點，傳入下一層的遞歸中。
算法流程：
1. 初始化一個全局的變量 prev，用來記錄中序遍歷過程中的前驅結點的val；
2. 中序遍歷的遞歸函數中：

設置遞歸出口：root == nullptr的時候，返回true；
先遞歸判斷左子樹是否是二叉搜索樹，用left標記
然后判斷當前節點是否滿足二叉搜索樹，用cur標記? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?如果當前節點的val大于prev，說明滿足條件，cur改為true? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?如果當前節點的val小于等于prev，說明不滿足條件，cur改為false? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
最后遞歸判斷右子樹是否是二叉搜索樹，用right標記

3.只有當left，cur，right都是true的時候，才返回true

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int prev;bool isValidBST(TreeNode* root) {if(root == nullptr)return true;bool left = isValidBST(root->left);//剪枝if(left == false)return false;bool cur = false;if(root->val > prev)cur = true;//剪枝if(cur == false)return false;prev = root->val; bool right = isValidBST(root->right);return left&&right&&cur;}
};

4.1題目鏈接：230.二叉搜索樹中第K小的元素

4.2題目描述：

給定一個二叉搜索樹的根節點?root?，和一個整數?k?，請你設計一個算法查找其中第?k?小的元素（從 1 開始計數）。

示例 1：

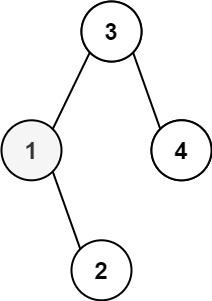
輸入：root = [3,1,4,null,2], k = 1
輸出：1

示例 2：

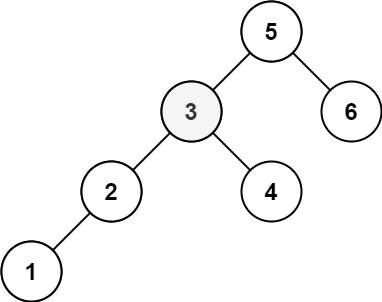
輸入：root = [5,3,6,2,4,null,null,1], k = 3
輸出：3

提示：

樹中的節點數為?n?。
1 <= k <= n <= 10^4
0 <= Node.val <= 10^4

4.3解法(中序遍歷+計數器剪枝)

算法思路：
我們可以根據中序遍歷的過程，只需掃描前k個結點即可。因此，我們可以創建一個全局的計數器count，將其初始化為k，每遍歷一個節點就將count--。直到某次遞歸的時候，count 的值等于 1，說明此時的結點就是我們要找的結果。

算法流程：
1. 定義一個全局的變量count，在主函數中初始化為k的值（不用全局也可以，當成參數傳入遞歸過程中）；

遞歸函數的設計：int dfs(TreeNode* root):
? 返回值為第k個結點；

遞歸函數流程(中序遍歷):
1. 遞歸出口：空節點直接返回-1，說明沒有找到；
2. 去左子樹上查找結果，記為 left：
????????a. 如果 left == -1，說明沒找到，繼續執行下面邏輯；
????????b. 如果 left ！= -1，說明找到了，直接返回結果，無需執行下面代碼（剪枝）
3. 如果左子樹沒找到，判斷當前結點是否符合：
????????a. 如果符合，直接返回結果
4.如果當前結點不符合，去右子樹上尋找結果

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int count;int ret = 1;int kthSmallest(TreeNode* root, int k) {count = k;dfs(root);return ret;}void dfs(TreeNode* root){if(root == nullptr||count == 0)return;dfs(root->left);count--;if(count==0)ret = root->val;dfs(root->right);}
};

5.1題目鏈接：257.二叉樹的所有路徑

5.2題目描述：

給你一個二叉樹的根節點?root?，按?任意順序?，返回所有從根節點到葉子節點的路徑。

葉子節點?是指沒有子節點的節點。

示例 1：

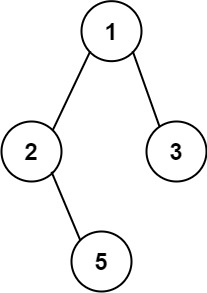
輸入：root = [1,2,3,null,5]
輸出：["1->2->5","1->3"]

示例 2：

輸入：root = [1]
輸出：["1"]

提示：

樹中節點的數目在范圍?[1, 100]?內
-100 <= Node.val <= 100

5.3解法(回溯)：

算法思路：
使用深度優先遍歷（DFS）求解。
路徑以字符串形式存儲，從根節點開始遍歷，每次遍歷時將當前節點的值加入到路徑中，如果該節點為葉子節點，將路徑存儲到結果中。否則，將"->”加入到路徑中并遞歸遍歷該節點的左右子樹。
定義一個結果數組，進行遞歸。遞歸具體實現方法如下：
????????1. 如果當前節點不為空，就將當前節點的值加入路徑 path 中，否則直接返回；
????????2. 判斷當前節點是否為葉子節點，如果是，則將當前路徑加入到所有路徑的存儲數組 paths 中；
????????3. 否則，將當前節點值加上“->"作為路徑的分隔符，繼續遞歸遍歷當前節點的左右子節點。
????????4. 返回結果數組。

?????????特別地，我們可以只使用一個字符串存儲每個狀態的字符串，在遞歸回溯的過程中，需要將路徑中的當前節點移除，以回到上一個節點。

具體實現方法如下：
1.定義一個結果數組和一個路徑數組。
2. 從根節點開始遞歸，遞歸函數的參數為當前節點、結果數組和路徑數組。
????????a. 如果當前節點為空，返回
????????b. 將當前節點的值加入到路徑數組中。
????????c.如果當前節點為葉子節點，將路徑數組中的所有元素拼接成字符串，并將該字符串存儲到結果數組中。
????????d. 遞歸遍歷當前節點的左子樹。
????????e. 遞歸遍歷當前節點的右子樹。
????????f.回溯，將路徑數組中的最后一個元素移除。以返回到上一個節點

3.返回結果數組

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> ret;vector<string> binaryTreePaths(TreeNode* root) {dfs(root,"");return ret;}void dfs(TreeNode* root, string path){path += to_string(root->val);if(root->left == nullptr&&root->right == nullptr){ret.push_back(path);return;}path += "->";if(root->left)dfs(root->left,path);if(root->right)dfs(root->right,path);}
};