圖像增強方法

• 目的：改善視覺效果，例如增強對比度
• 定義：為了改善視覺效果、便于人或計算機對圖像的分析理解，針對圖像的特點或存在的問題，采取的改善方法或加強特征的措施。
• 本質：有選擇地加強圖像中的某些信息，抑制另一些信息，產生一幅新的圖像
• 增強方法的分類：空間與方法，頻域方法，混合域方法
• 空間域方法：直方圖，回復直方圖是灰度的概率密度，橫坐標為灰度，縱坐標為每種灰度的像素頻率
  • 通常情況下，若一幅圖像的像素傾向于占據整個可能的灰度級并且分布均勻，則該圖像會有高對比度的外觀$\to$直方圖均衡化：找到一種變換使得變換后的概率密度函數均勻分布。$$s_k^{\prime }=T(r_k)=\sum _{j=0}^{k}P(r_j)$$
  • 直方圖均衡化的實質：占有較少像素的灰度變換后被歸并；直方圖均衡化的缺點：由于灰度歸并，可能損失一些圖像細節；處理后的圖像顯得粗獷。
• 頻域方法
  • 二維傅里葉變換
    $$F(u,v)=\frac{1}{MN}\sum _{x=0}^{M?1}\sum _{y=0}^{M?1}f(x,y)exp[?j2\pi (\frac{ux}{M}+\frac{vy}{N})]u=0,1,\dots ,M?1,v=0,1,\dots ,N?1$$
  • 二維傅里葉變換的物理意義：
    類比一維傅里葉變化，二維傅里葉變化的本質在于將圖像分解成若干個平面正弦波之和。
  • 二維正弦波的確定需要四個參數：幅值、頻率、相位、方向。
  • 高頻分量代表圖像中的邊緣、細節等內容；低頻分量代表圖像中緩慢變化的內容。
  • 同態濾波：目的：改善圖像中偏暗的區域。 模型：建立圖像的反射成像模型為：$$f(x,y)=i(x,y)r(x,y)$$
    $i(x,y)$:照度分量，緩慢變化，對應于低頻部分；$r(x,y)$:反射分量，快速變化，對應于高頻部分。 方法：為增強較暗部分的細節，將圖像轉到頻域，設計頻域濾波函數，減弱圖像的低頻分量，加強高頻分量。
• 同態濾波步驟：
  • 根據反射成像模型，有：$f(x,y)=i(x,y)r(x,y)$；
  • 兩邊取對數：$lnf(x,y)=lni(x,y)+lnr(x,y)$
  • 兩邊取傅氏變換：$F(u,v)=I(u,v)+R(u,v)$
  • 用同態濾波函數$H(u,v)$處理$F(u,v)$：$$H(u,v)F(u,v)=H(u,v)I(u,v)+H(u,v)R(u,v)$$
  • 兩邊取反傅氏變換：$f^{\prime }(x,y)=i^{\prime }(x,y)+r^{\prime }(x,y)$
  • 兩邊取指數：$g(x,y)=exp|f^{\prime }(x,y)|$
• 為什么叫同態濾波？同態系統：通過非線性變換將非線性組合信號變換為線性組合信號，以便于進行線性處理的一類系統的總稱。

圖像復原方法

• 圖像復原的目的：恢復出最接近原始圖像的輸出圖像

• 圖像復原的概念

  • 圖像退化：圖像獲取過程可能出現模糊、畸變、噪聲，使圖像降質的現象。
  • 圖像復原：根據退化模型和先驗信息，按照某種準則，從退化圖像恢復出最接近原始圖像的輸出圖像。
  • 與圖像增強的區別：圖像復原會用到先驗信息。

• 圖像退化的原因：

  • 相機與景物之間存在相對運動，造成運動模糊
  • 圖像在成像、采集、處理過程中，引入噪聲
  • 光學系統的像差、鏡頭畸變、帶寬有限，造成圖像失真
  • 相機掃描機構的非線性，引起幾何失真
  • 光學系統或探測器特性不均勻，造成相同亮度的景物表現出不同灰度（灰度失真）
  • 傳輸介質（如大氣湍流、大氣成分變化）引起輻射失真

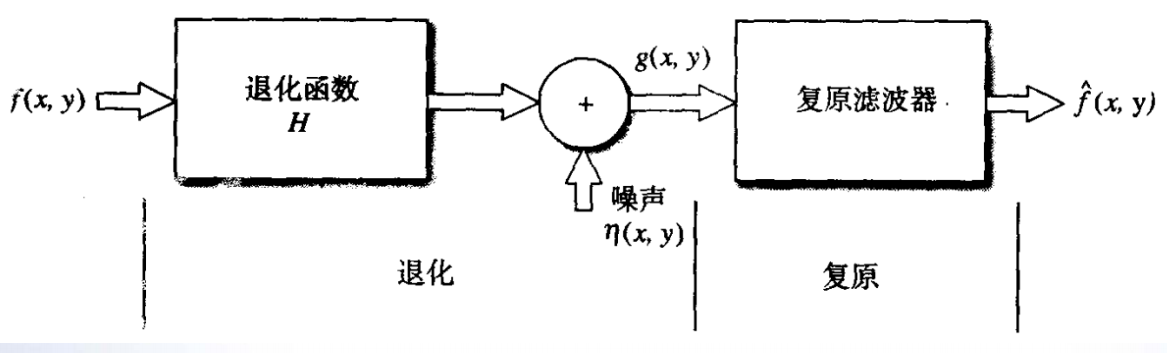
• 圖像退化和復原的過程建模：

  • $$\begin{gathered} g(x,y)=H[f(x,y)]+n(x,y) \\ f(x,y)=P[g(x,y)] \end{gathered}$$

• 圖像去噪：噪聲：在成像、數字化、采集和處理過程中產生的；會擾亂圖像的可觀測信息。噪聲的描述與建模：噪聲類型由產生噪聲的物理過程決定，通常用特定的概率密度函數(PDF)建模。 高斯噪聲：高溫引起的傳感器噪聲（熱噪聲）脈沖噪聲：電磁干擾以及通信系統的故障和缺陷（雪花噪聲）瑞利噪聲。指數噪聲。

  • 圖像去噪的分類： 空域濾波方法：均值濾波器；統計排序濾波器； 頻域濾波方法：帶阻濾波器、帶通濾波器、陷波濾波器
  • 空域濾波：使用空域模板進行的圖像處理。模板又被稱為空域濾波器。$$g(x,y)=\sum _{s=?a}^a\sum _{t=?b}^{b}w(s,t)f(x+s,y+t)$$
  • 均值濾波的作用 減小圖像灰度的“尖銳”變化，減小噪聲；由于圖像邊緣是由圖像灰度尖銳變化引起的，所以也存在邊緣模糊的問題。
  • 統計排序濾波器：以目標像素鄰域的像素值排序結果代替中心像素的值。最大值濾波器：用像素領域內的最大值代替該像素（去除胡椒噪聲）；最小值濾波器：用像素領域內的最小值代替該像素（去除鹽噪聲）；中值濾波器：用像素領域內的中間值代替該像素（去除脈沖噪聲）

• 退化模型估計：在退化函數H滿足線性性、位置不變性的條件下，圖像退化過程可以表示為：一個空域濾波器 h(x,y) 在圖像 f(x,y) 上的卷積。

  • 圖像觀察估計：只有退化圖像的信息，沒有任何關于退化函數的信息。
  • 試驗估計：在具有相同的裝置，且能夠進行重復試驗的情況下
  • 建模估計：知道引起圖像退化的物理特性/機理，且能夠使用數學模型進行表示時可使用該方法。
  • 以運動模糊為例：正常拍照情況下，如果畫面是f(x,y)，假設曝光時間為T，則成像g(x,y)的表達式如下：$$g(x,y)={\int }_0^{T}f(x,y)dt=Tf(x,y)$$ 傳感器上成的像，是畫面在曝光時間下累積在傳感器上的能量。

• 逆濾波復原
  

• 維納濾波復原：使復原圖像與原始圖像的均方誤差最小，即：$$\min ({\epsilon }^2)=\min (E\left\{{\left[f(x,y)?\hat{f}(x,y)\right]}^2\right\})$$

• 維納濾波 v.s.逆濾波 無噪聲時，$S_{nn}(u,v)=0$，維納濾波即為逆濾波。有噪聲時，維納濾波用噪信功率比對恢復過程進行修正。

圖像分割方法

• 圖像分割的目的：將目標從背景中分離出來。
• 圖像分割與圖像語義分割的區別：圖像分割的結果不需要提供區域的語義類別信息。
• 根據灰度、顏色、紋理、形狀等特征，將圖像分成若干個區域｛S1, S2 … Sn｝，讓區域間顯差異性，區域內呈相似性。
• 正確的區域分割必須滿足以下條件：
  • 圖像分割的完整性：圖像中的像素無一漏網：
  • 區域之間互不相交
  • 同一區域內特征一致
  • 相鄰區域特征不一致
  • $$\begin{array}{c}X={?}_{i=1}^{n}S,\\ S_i\cap S_j=\Phi ,\\ P(S_i)=True,\\ P(S_1\cup S_2)=False\end{array}$$
• 圖像分割的輸出：一般為二值圖像
• 區域：在數字圖像中，每個像素周圍有8個鄰接像素，常見的鄰接關系有3種：4鄰接、8鄰接、混合鄰接。若兩個像素之間有一條通路能通過鄰接關系把它們連接
  起來，那么這兩個像素就是連通的。彼此連通的點形成了的集合稱為連通區域。
• 圖像分割的實質：對圖像的特征空間進行劃分
• 以灰度特征為例，圖像分割的基本思路：①、以尋找區域間的不一致性為出發點 基于邊緣的分割方法。②、以尋找區域內的一致性為出發點 基于閾值的分割方法 基于區域的分割方法 基于聚類的分割方法
• 基于邊緣的分割方法：邊緣意味著一個區域的終結，和另一個區域的開始。
• 基于閾值的分割方法：確定灰度閾值，并將圖像中每個像素的灰度值與閾值進行比較，根據比較結果將像素分配到合適的類別中。關鍵問題在于灰度閾值的確定。單閾值分割：針對圖像中只有目標和背景的情況。
  • 單閾值分割：針對圖像中只有目標和背景的情況。
  • 確定閾值的三種方法：手動閾值分割；直方圖雙峰法；自適應閾值圖像分割。
    • 直方圖雙峰法：已知圖象僅包含具有明顯灰度差別的目標和背景，此時灰度直方圖通常為雙峰單谷型，取谷底點為閾值即可完成分割。
    • 自適應閾值圖像分割：定義一種準則，自動求解閾值，使得分割結果滿足上述準則。迭代法和大津法
• 基于區域的分割方法
  • 區域生長：將每個像素與鄰域中足夠相似的像素連接，完成圖像分割。關鍵：確定生長準則 or 相似性度量。灰度差；相對灰度差（像素間灰度差/鄰域標準差）
  • 區域分割與聚合：按照特定的準則將圖像分割成一系列任意不相關的區域，然后將它們合并以滿足限制條件。
  • 分水嶺分割算法：地形圖(topographic map)：地表起伏形態和地理位置、形狀在水平面上的投影圖。 每幅圖像都是一幅“地形圖”，以圖像長寬為x，y軸，以像素亮度為z軸。模擬自底向上逐漸淹沒地形過程。當兩個山谷的水將要匯合時，在匯合處建立堤壩，直到整個
    地形都被淹沒，從而就得到了各個堤壩(分水嶺)和一個個被堤壩分開的盆地(目標物體)。
• 基于聚類的分割方法：尋找不同“類別”的中心點
• 拓展：基于圖理論的分割方法

形態學處理

• 以形態為基礎對圖像進行分析。簡化圖像數據，保持它們基本的形狀特性，并除去不相干的結構。
• 形態學處理的數學基礎是集合論
• 集合運算：映像、位移
• 形態學處理的基本思想：采用一定形態的結構元素B，去度量和提取圖像A中物體的形狀。
• 形態學處理的基本運算：膨脹、腐蝕、開操作、閉操作。
  • 膨脹運算定義為集合 $A$ 與結構元素 $B$ 的平移并集：
    A⊕B={z∣(B^)z∩A≠?}A \oplus B = \{ z | (\hat{B})_z \cap A \neq \emptyset \} A⊕B={z∣(B^)z?∩A=?}
    其中 $\hat{B}$ 表示 $B$ 的反射（對稱集），$(\hat{B}{)}_z$ 表示 $B$ 平移 $z$ 后的集合。
    膨脹的目的是將二值化圖像的邊界向外擴張，擴張的方式由結構元素
    決定。
  • 腐蝕運算定義為結構元素 $B$ 完全包含在集合 $A$ 中的所有平移點：
    A?B={z∣Bz?A}A \ominus B = \{ z | B_z \subseteq A \} A?B={z∣Bz??A}
    其中 $B_z$ 表示 $B$ 平移 $z$ 后的集合。
    目的：將二值圖像中物體的邊界向內收縮，使其“腐蝕”。
  • 開操作是先腐蝕后膨脹的復合運算：
    $$A°B=(A?B)\oplus B$$
    目的為斷開圖像中狹窄的連接和消除細的突出物。
  • 閉操作是先膨脹后腐蝕的復合運算：
    $$A?B=(A\oplus B)?B$$
    目的：消除圖像中小的孔洞，并填補輪廓線中的斷裂。
• 基本運算的應用：邊界提取、區域填充、連通分量的提取、細化、粗化
• 形態學應用中，結構元素的形狀由具體任務確定
• 形態學可以拓展至灰度圖像：二值形態學中用到的和并運算在灰度形態學中分別用最大極值和最小極值運算代替。