數據結構 | 超詳細講解七大排序（C語言實現，含動圖，多方法！）

目錄

?編輯

排序的概念

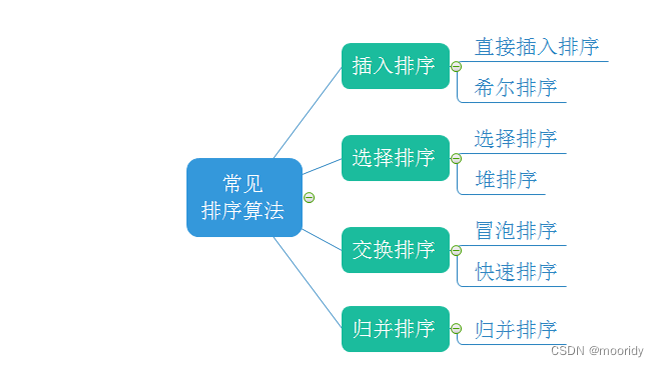
常見排序算法

?編輯

1.冒泡排序

🍹圖解

🥳代碼實現

🤔時間復雜度

2.插入排序

🍹圖解

🌴深度剖析

🍎代碼思路

🥳代碼實現

🤔時間復雜度

3.希爾排序

🌴深度剖析

🍎代碼思路

🍋思考：關于gap的取值問題

🥳代碼實現

🤔時間復雜度

4.堆排序

??請看我的另一篇文章：詳解堆排序

5.選擇排序

🍹圖解

🌴深度剖析

🥳代碼實現

🤔時間復雜度

6.快速排序

🍹圖解1：霍爾法

🌴深度剖析

🍎代碼思路

🍎優化1：改變選key策略，采用三數選中法

🍎優化2：小區間優化，采用其它排序方法，減少遞歸次數

🍋思考：如何保證相遇位置比key小？

🥳代碼實現

🍹圖解2：前后指針法

?🌴深度剖析

🍎代碼思路

🍎優化：避免自己和自己交換

🥳代碼實現

🍹非遞歸實現

🍎代碼思路

🥳代碼實現

7.歸并排序

🍹圖解

🌴深度剖析

🍹遞歸版

🍎代碼思路

🥳代碼實現

🍹非遞歸版

🍎代碼思路

🍋思考：上面的思路只能解決數組大小為的數組，其余數組則會存在越界問題，如何解決？

🥳代碼實現

🤔時間復雜度

排序的概念

排序 ：所謂排序，就是使一串記錄，按照其中的某個或某些關鍵字的大小，遞增或遞減的排列起來的操作。
穩定性 ：假定在待排序的記錄序列中，存在多個具有相同的關鍵字的記錄，若經過排序，這些記錄的相對次
序保持不變，即在原序列中， r[i]=r[j] ，且 r[i] 在 r[j] 之前，而在排序后的序列中， r[i] 仍在 r[j] 之前，則稱這種排
序算法是穩定的；否則稱為不穩定的。
內部排序 ：數據元素全部放在內存中的排序。
外部排序 ：數據元素太多不能同時放在內存中，根據排序過程的要求不斷地在內外存之間移動數據的排序。

常見排序算法

下文將會細細介紹上圖中七種排序，觀看前，可以點一個免費的贊與收藏支持作者~希望本篇博客能幫助到你！

1.冒泡排序

相鄰兩個數進行比較，大的數向后移，每次循環都能冒出一個大的數到數組最后，直至最后全部冒出。

🍹圖解

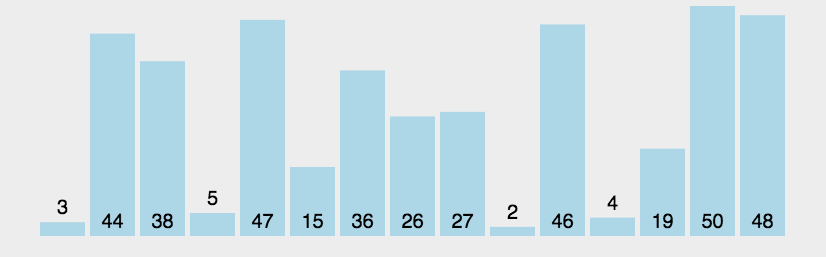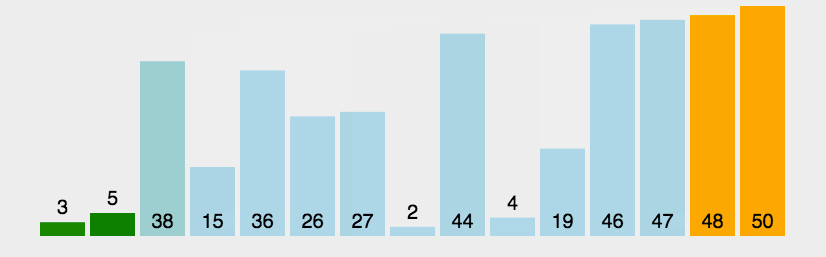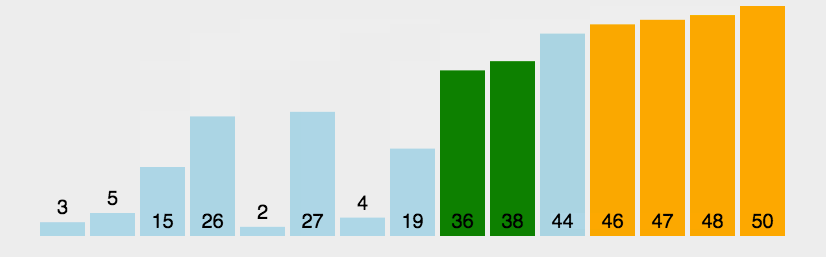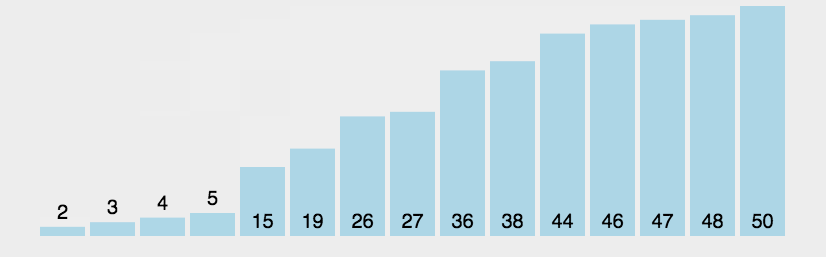
🥳代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>void bubble_sort(int arr[],int sz)
{int flag = 1;//優化int i = 0;for (i = 0; i < sz - 1; i++) {int j = 0;for (j = 0; j < sz - 1 - i; j++) {if (arr[j] > arr[j + 1]) {flag = 0;int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;}}if (flag == 1) {break;}}
}int main() {int n = 0;int arr[] = {2,6,9,3,6,9,1};int sz = sizeof(arr) / sizeof(arr[0]);bubble_sort(arr, sz);for (n = 0; n < sz - 1; n++) {printf("%d", arr[n]);}return 0;
}

🤔時間復雜度

O(N^2)

2.插入排序

🍹圖解

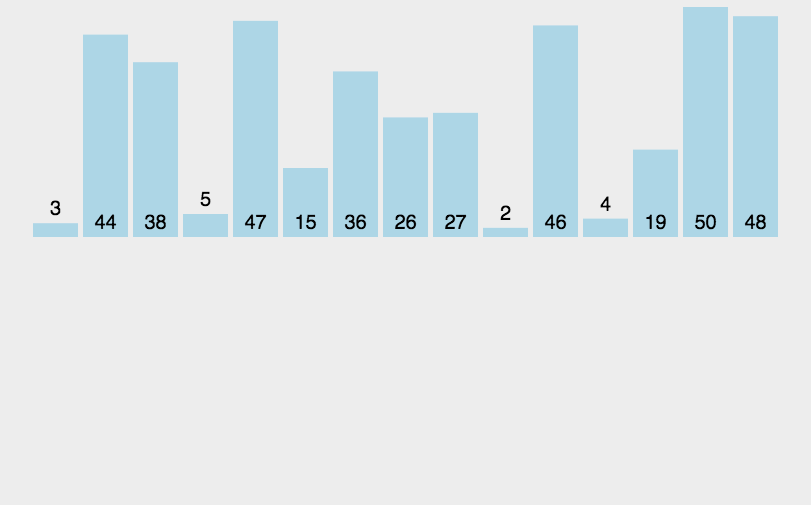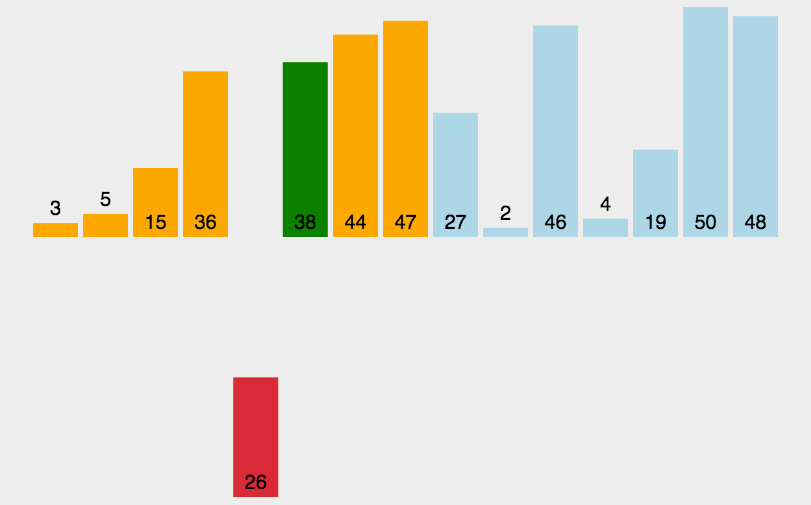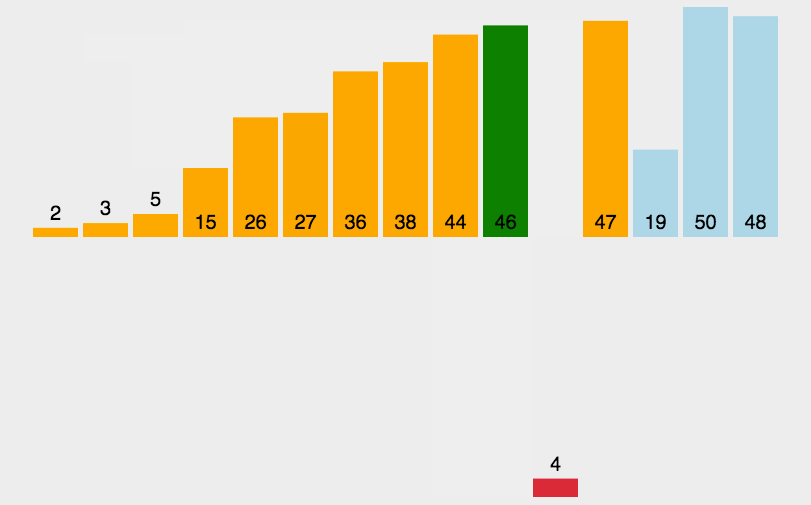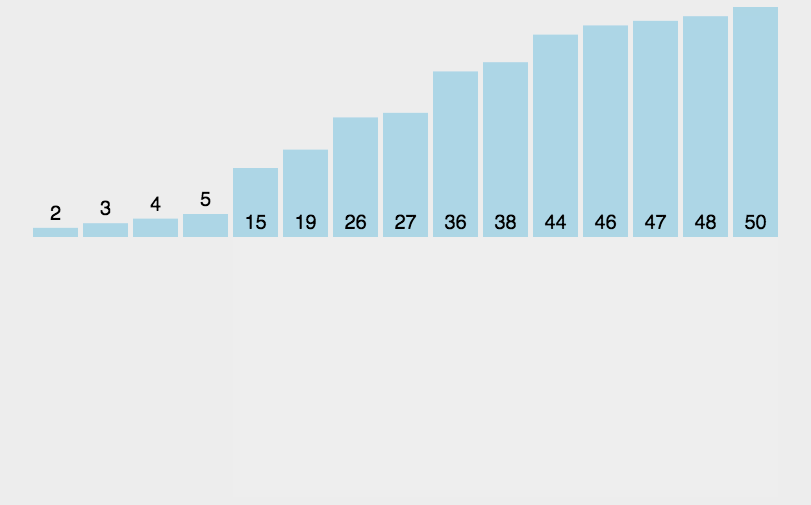
🌴深度剖析

🍎代碼思路

上圖為基本的插入排序，可對其進行優化：依次遍歷找出最大值和最小值索引。

代碼思路：1.設變量mini，maxi分別為最小值和最大值索引

? ? ? ? ? ? ? ? ? ? ?設begin，end分別無序部分的首尾索引。

? ? ? ? ? ? ? ? ? 2.遍歷無序部分，找出最小值和最大值的索引mini，maxi

? ? ? ? ? ? ? ? ? 3.將a[begin]和a[mini]進行交換，將a[end]和a[maxi]進行交換

? ? ? ? ? ? ? ? ? ? ?注意：兩次交換的中間需要進行依次判斷，判斷maxi是否仍然等于begin，因為經過第一個交換后原begin位置的值已經交換到mini位置去了，如果判斷成立，maxi也應該跟隨原begin的值的移動移動到mini位置。

? ? ? ? ? ? ? ? ? 4.此時begin、end處已經屬于有序部分，begin++,end--，，更新無序部分的范圍。

? ? ? ? ? ? ? ? ?5.對剩余無序部分重復上述步驟，直到begin==end。

🥳代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}void selectsort(int* a, int n) {int begin = 0;int end = n - 1;while (begin < end) {int mini = begin;int maxi = begin;//找最大值最小值的索引for (int i = begin + 1; i <= end; i++) {if (a[i] < a[mini]) {mini = i;}if (a[i] > a[maxi]) {maxi = i;}}//進行交換swap(&a[mini], &a[begin]);if (maxi == begin)//begin此時被mini換走了maxi = mini;swap(&a[maxi], &a[end]);begin++;end--;}}int main() {int a1[8] = { 9,1,2,5,7,4,6,3};selectsort(a1,8);//int a2[5] = { 3,2,5,6,7 };//selectsort(a2, 5);for (int i = 0; i < 8; i++) {printf("%d ", a1[i]);}return 0;
}

🤔時間復雜度

O（N^2)

3.希爾排序

🌴深度剖析

🍎代碼思路

希爾排序是在插入排序的基礎上進行優化的。

1.預排序：將數組分為gap組，進行預排序（讓數組接近有序）

2.插入排序（此時，數組近乎有序，使用插入排序效率極高）

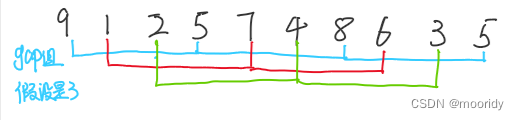
即藍色的為一組，紅色的為一組，綠色為一組，對每組進行插入排序

以下是預排序的代碼：

//預排序過程，假設gap=3
//第一種寫法：依次對三組進行預排序
for(int j=0;j<gap;j++){   //依次對三組進行預排序
for (int i = gap; i < n; i+=gap) {  //對一組進行預排序的過程，由于一組內部元素之間相距gap，所以應該是i+=gapint end = i;int tmp = a[end];while (end >= gap) {if (tmp < a[end - gap]) {a[end] = a[end - gap];a[end - gap] = tmp;end -= gap;}else {break;}} }
//第二種寫法：同時進行三組的預排序（但效率相較上一種寫法其實沒有改變）
for (int i = gap; i < n; i++) {//先對藍組排1下，再對紅組排1下，再對綠組排1下，如此循環int end = i;int tmp = a[end];while (end >= gap) {if (tmp < a[end - gap]) {a[end] = a[end - gap];a[end - gap] = tmp;end -= gap;}else {break;}}

🍋思考：關于gap的取值問題

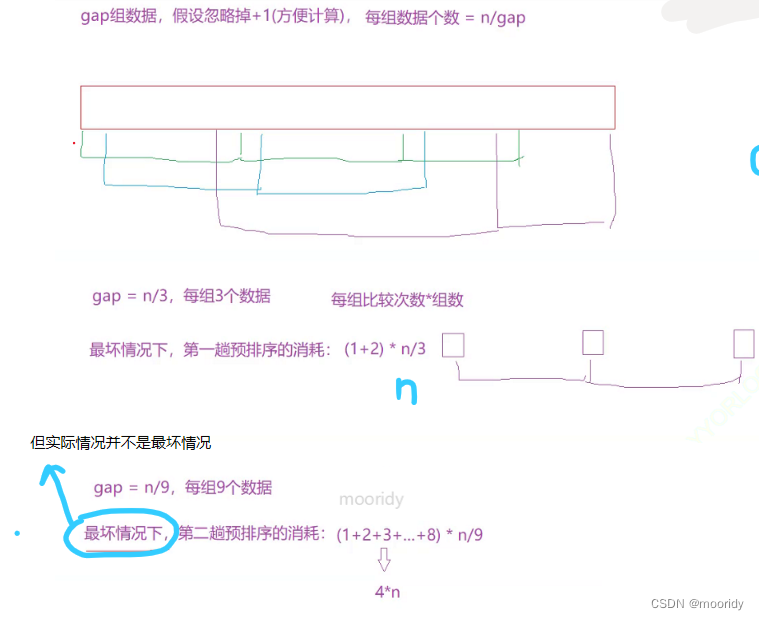
gap越大：大的數字越快跳到后面，小的數字越快跳到前面，結果越不接近有序。

gap越小：跳得越慢，但結果越接近有序（gap==1時，相當于插入排序)

解決方案：走多組gap，gap>1時就是預排序

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? gap==1時就是插入排序

gap我們通常設置為gap=gap/3+1

這里＋1是為了保證gap>=1。

🥳代碼實現

//1.預排序，分成gap組進行//2.插入排序void ShellSort(int* a, int n) {int gap = n;while (gap>1) {gap = gap / 3 + 1;//保證gap>=1for (int i = gap; i < n; i++) {int end = i;int tmp = a[end];while (end >= gap) {if (tmp < a[end - gap]) {a[end] = a[end - gap];a[end - gap] = tmp;end -= gap;}else {break;}}}}}

🤔時間復雜度

4.堆排序

??

請看我的另一篇文章：詳解堆排序

5.選擇排序

🍹圖解

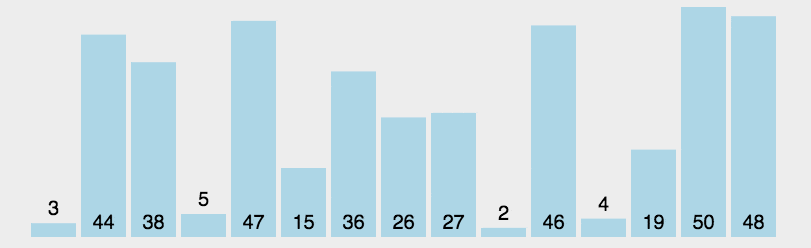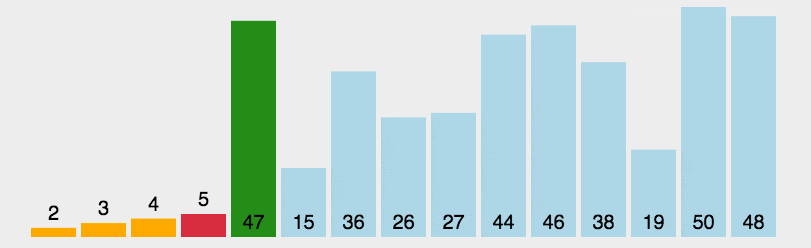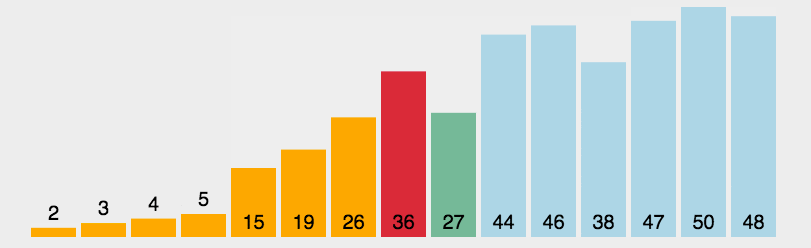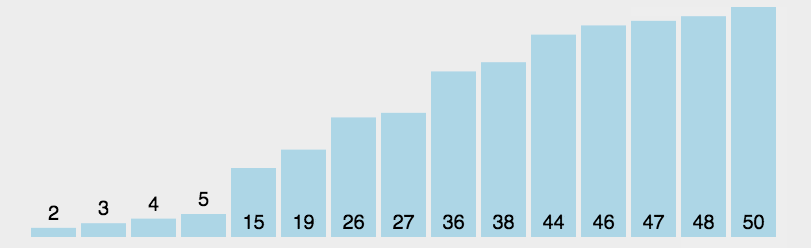
🌴深度剖析

基本思路：遍歷一遍，選擇最小的插到最左邊

優化思路：遍歷一遍，選出最小的最大的分別插到最左最右

一個小坑：將最大值放到最后后，可能破壞了原本的

🥳代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}void selectsort(int* a, int n) {int begin = 0;int end = n-1 ;while (begin < end) {int mini = a[begin];int maxi = a[end];for (int i = begin; i <= end; i++) {if (a[i] < mini) {mini = a[i];swap(&a[i], &a[begin]);}if(a[i]>maxi) {maxi = a[i];swap(&a[i], &a[end]);}//驗證if (a[i] <= mini) {mini = a[i];swap(&a[i], &a[begin]);}}begin++;end--;}}int main() {int a1[8] = { 9,1,2,5,7,4,6,3};selectsort(a1,8);//int a2[5] = { 3,2,5,6,7 };//selectsort(a2, 5);for (int i = 0; i < 8; i++) {printf("%d ", a1[i]);}return 0;
}

🤔時間復雜度

O（N^2)

6.快速排序

🍹圖解1：霍爾法

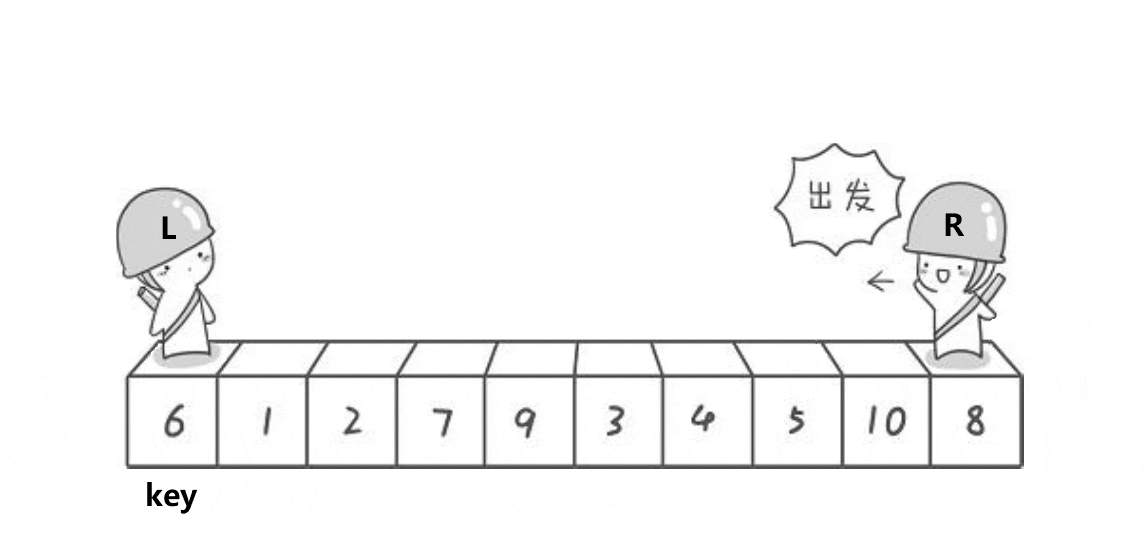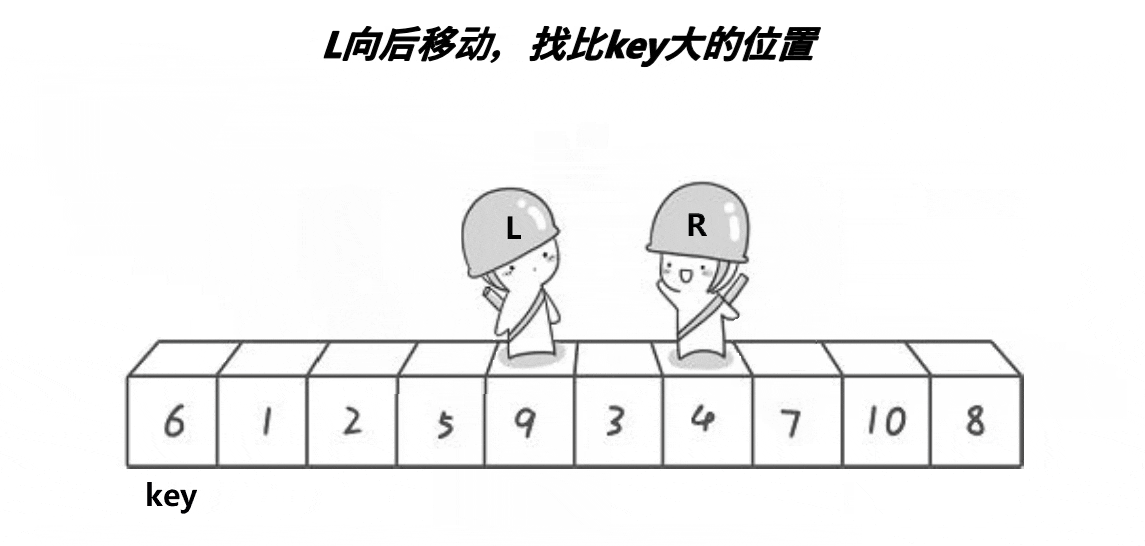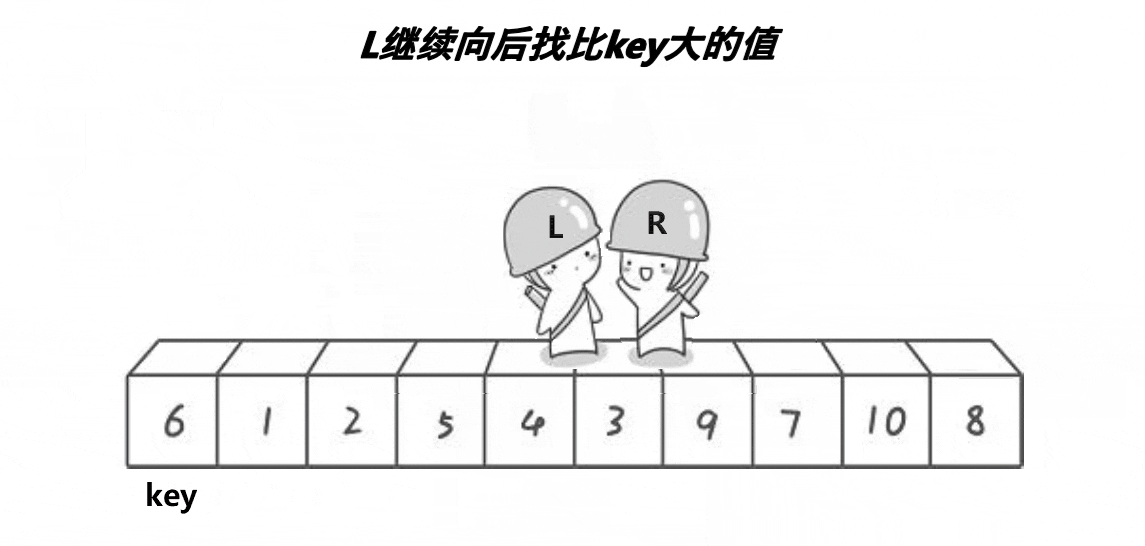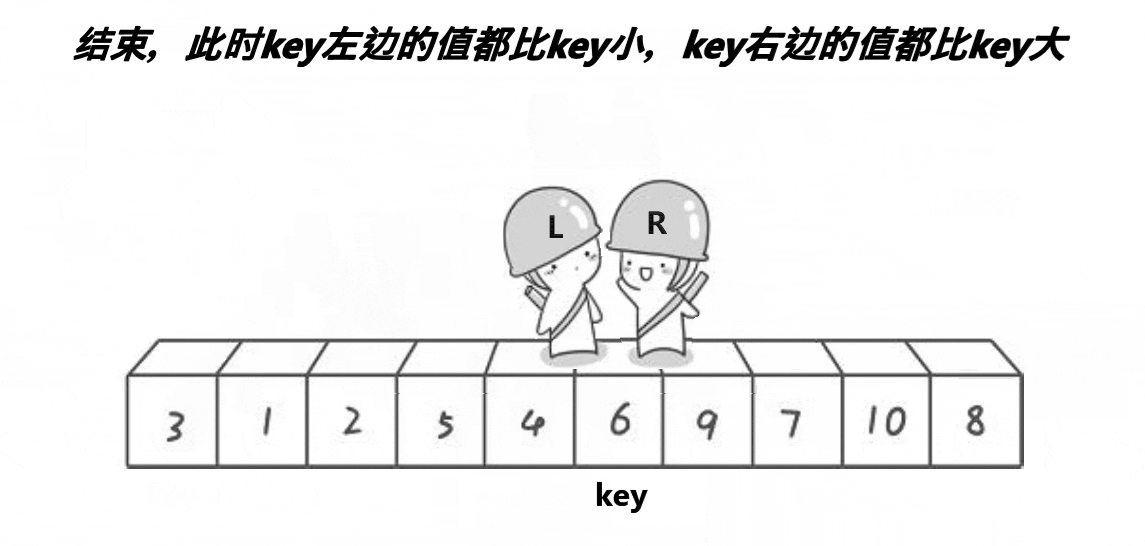
🌴深度剖析

🍎代碼思路

我們先考慮單趟：
?? ?end,begin相遇前：end向前走找比key小的值，begin向后走找比key大的值，都找到后兩者進行交換
?? ?end,begin相遇時：循環停止，交換begin和key

??單趟過后的結果：

key所在位置一定是正確的位置，[left,key-1]中的值一定小于key，[key+1,right]中的值一定大于key

//單趟（一定先走end,再走begin）
int begin = left;int end = right;int key = left;while (begin < end) {while (a[end] >= a[key] && begin < end) {end--;}while(a[begin] <= a[key]&&begin<end) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[key]);
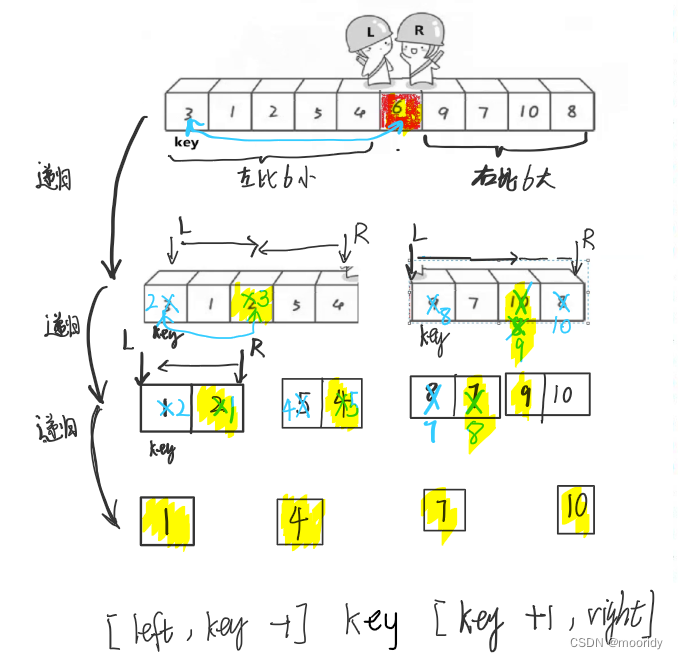
key = begin;

此時整個數組可以劃分為三個部分：[left,key-1]，key,? ?[key+1,right]

遞歸：接著就用遞歸思想對[left,key-1]，[key+1,right]中的值進行排序
??遞歸結束條件：數組不存在或者只有1個元素

🍎優化1：改變選key策略，采用三數選中法

當數組有序排列時，且數據量較大時，基礎版快排可能出現棧溢出問題。

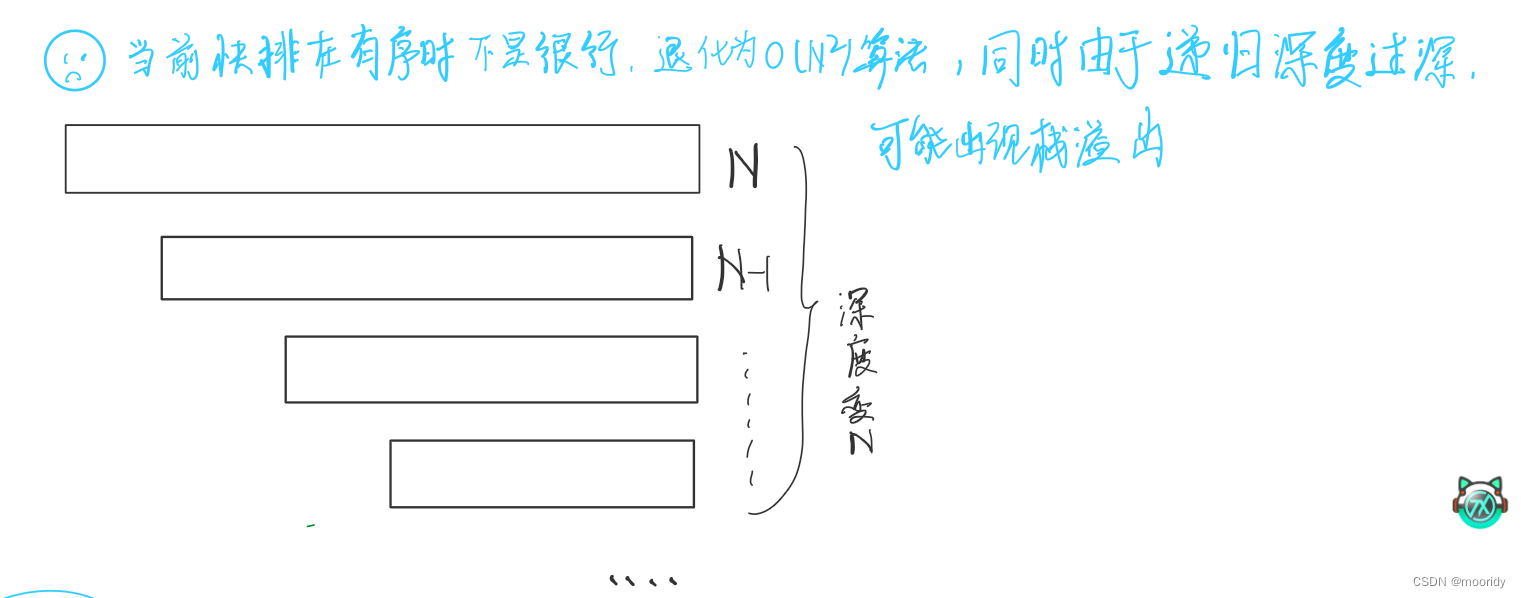
解決辦法:改變選key的策略，采用三數選中的方法，使key不要老是為最小值，而盡量趨于中值。

即確定出三個索引，如left，right, (right-left)/2，選出三個索引對應的值為中值的索引。

//優化1：改變選key的策略，采用三數選中法
int FindMid(int* a, int left, int right) {int mid = (left + right) / 2;if (a[left] < a[right]) {if (a[left] < a[mid]) {if (a[mid] < a[right]) {//a[left]<a[mid]<a[right]return mid;}else {//a[left]<a[right]<a[mid]return right;}}else {//a[mid]<a[left]<a[right]return left;}}else {//a[left] > a[right]if (a[mid] > a[right]) {if (a[mid] > a[left]) {//a[mid] > a[left]> a[right]return left;}else {return mid;}}else {//a[left] > a[right]>a[mid]return right;}}
}

🍎優化2：小區間優化，采用其它排序方法，減少遞歸次數

冒泡排序、選擇排序效率太一般，希爾排序更適合處理數據量更大的數據，此時的數據已經較為接近有序，此處采用插入排序。

	//優化：小數區間，采取選擇排序if (left + 5 >= right) {InsertSort(a+left, right - left + 1);return;}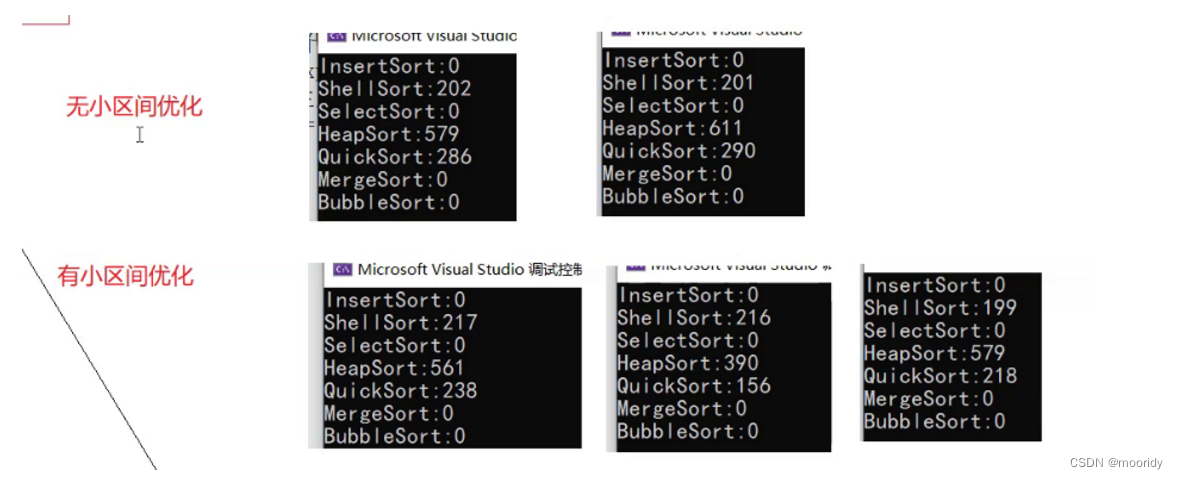

🍋思考：如何保證相遇位置比key小？

左邊做key，右邊先走，可以保證相遇位置比key小。

相遇場景分析：

begin遇end：end先走，停下來，一定是因為遇到了比key小的值。

? ? ? ? ? ? ? ? ? ? ? begin再走，begin沒有找到大的遇到end就停下了。

end遇begin：end走，end沒有找到小的遇到begin就停下了。

? ? ? ? ? ? ? ? ? ? ? 而begin的位置此時還是上一輪交換的位置，而上一輪交換，把比key小的值換到了begin的位置。

🥳代碼實現

1.基礎版（遞歸）

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
//遞歸版
void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}
void QuickSort(int* a, int left, int right) {//先考慮單趟//end找比key小，begin找比key大，都找到后交換//end,begin相遇時停止，交換begin和key//單趟過后的結果：key所在位置一定是正確的位置，a[left,key-1]一定小于key，a[key+1,right]一定大于key//接著就用遞歸思想處理：a[left,key-1]，a[key+1,right]//遞歸結束條件：數組不存在或者只有1個元素if (left >= right) {return;}int begin = left;int end = right;int key = left;while (begin < end) {while (a[end] >= a[key] && begin < end) {end--;}while(a[begin] <= a[key]&&begin<end) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[key]);key = begin;//此時key需要改變QuickSort(a, left, key-1);QuickSort(a, key + 1,  right);
}int main() {int a[10]={ 6, 1, 2, 7, 9, 3, 4, 5, 10,8 };QuickSort(a, 0, 9);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}return 0;
}

2.優化版（遞歸）

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
//遞歸版
void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}
//優化1：改變選key的策略，采用三數選中法
int FindMid(int* a, int left, int right) {int mid = (left + right) / 2;if (a[left] < a[right]) {if (a[left] < a[mid]) {if (a[mid] < a[right]) {//a[left]<a[mid]<a[right]return mid;}else {//a[left]<a[right]<a[mid]return right;}}else {//a[mid]<a[left]<a[right]return left;}}else {//a[left] > a[right]if (a[mid] > a[right]) {if (a[mid] > a[left]) {//a[mid] > a[left]> a[right]return left;}else {return mid;}}else {//a[left] > a[right]>a[mid]return right;}}
}void InsertSort(int* a, int n) {for (int i = 1; i < n ; i++) {int end = i;int tmp = a[end];while (end > 0) {if (tmp < a[end - 1]) {a[end] = a[end - 1];a[end - 1] = tmp;end--;}else {break;}}}
}void QuickSort(int* a, int left, int right){//先考慮單趟//end找比key小，begin找比key大，都找到后交換//end,begin相遇時停止，交換begin和key//單趟過后的結果：key所在位置一定是正確的位置，a[left,key-1]一定小于key，a[key+1,right]一定大于key//接著就用遞歸思想處理：a[left,key-1]，a[key+1,right]//遞歸結束條件：數組不存在或者只有1個元素/*if (left >= right) {return;}*///優化：小數區間，采取選擇排序if (left + 5 >= right) {InsertSort(a+left, right - left + 1);return;}int begin = left;int end = right;//優化：改變選key的策略，采用三數選中法int key = FindMid(a+left, left, right);Swap(&a[begin], &a[key]);key = begin;//int key = begin;while (begin < end) {while (a[end] >= a[key] && begin < end) {end--;}while(a[begin] <= a[key]&&begin<end) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[key]);key = begin;//此時key需要改變QuickSort(a, left, key-1);QuickSort(a, key + 1,  right);
}int main(){int a[10]={ 6, 1, 2, 7, 9, 3, 4, 5, 10,8 };QuickSort(a, 0, 9);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}return 0;
}

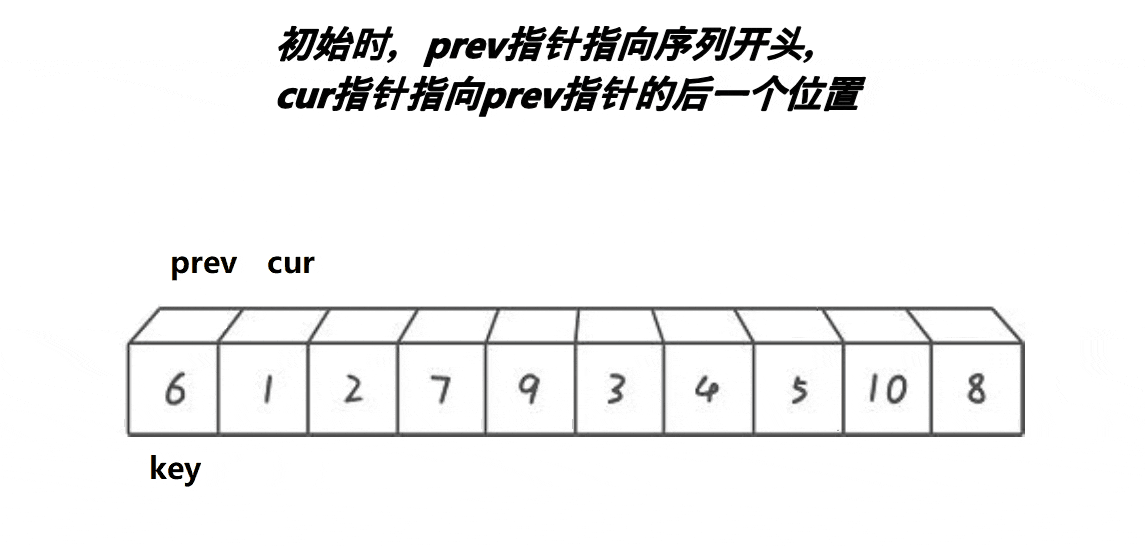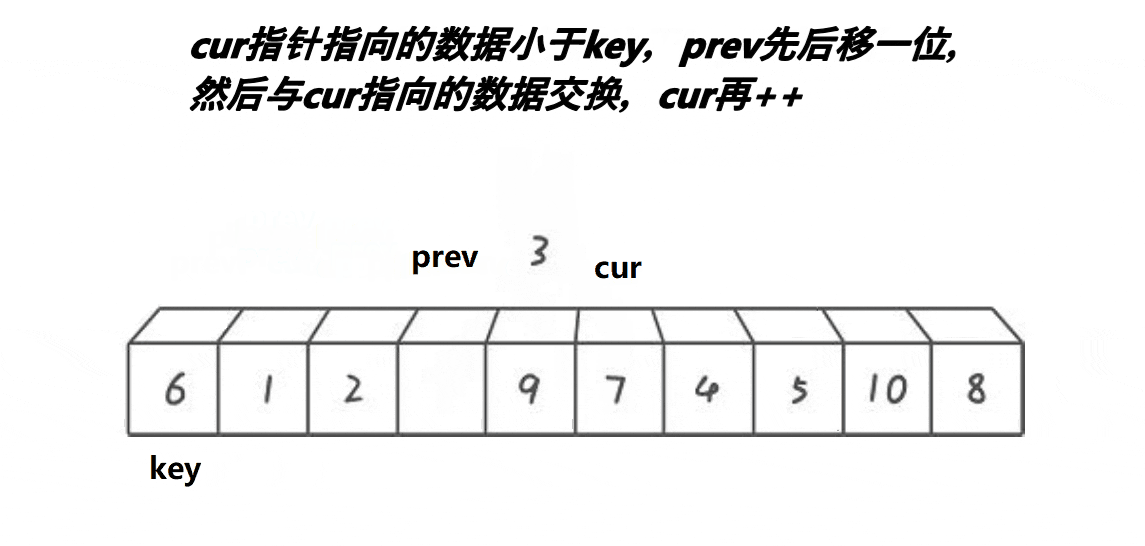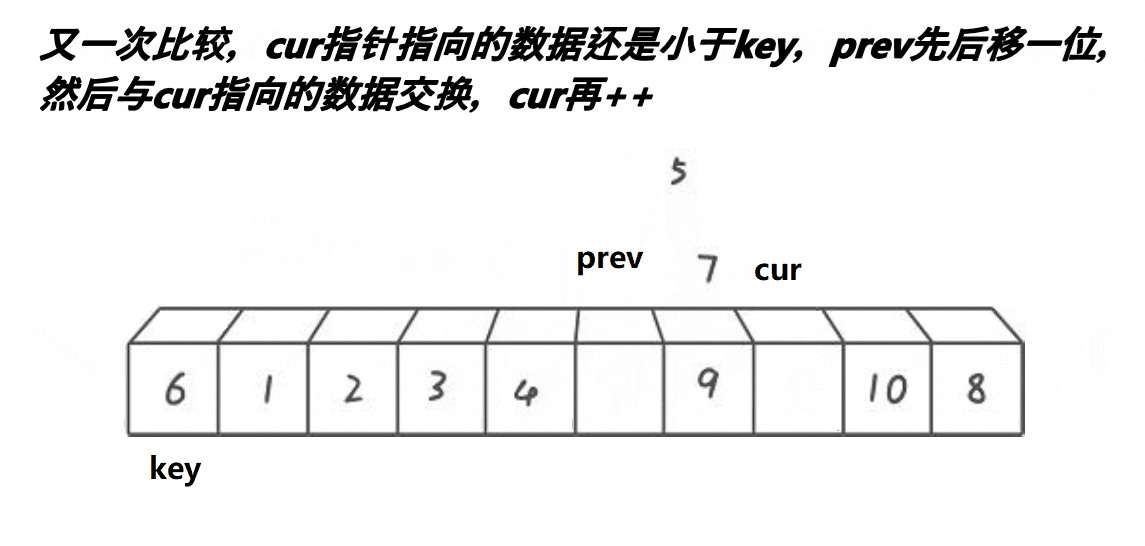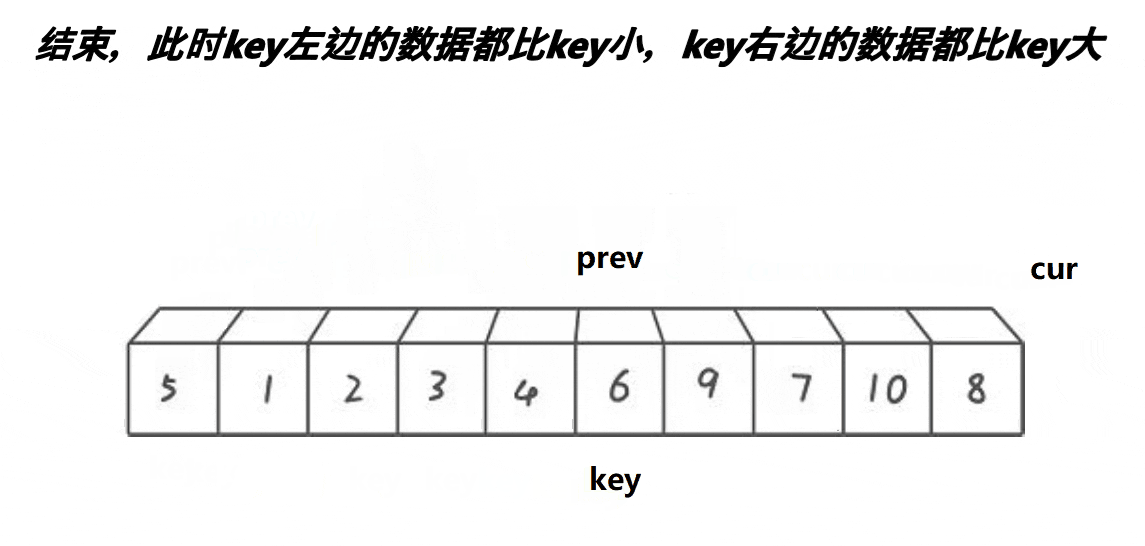
🍹圖解2：前后指針法

?🌴深度剖析

🍎代碼思路

仍然從單趟開始分析：

1.

2.判斷cur指針指向的數據是否小于key：

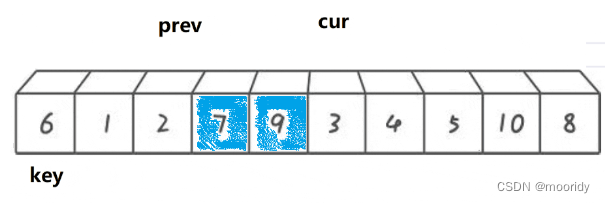
? 小于——prev后移一位，交換cur和prev指向的內容，cur指針后移一位

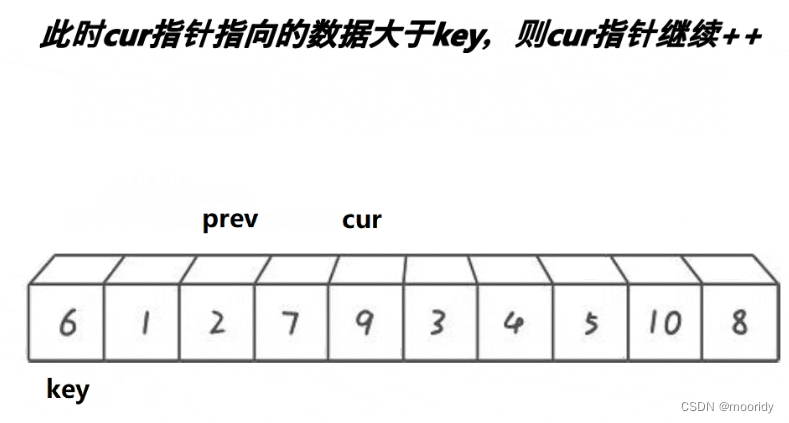
大于——cur后移一位，效果：使得prev和cur之間的值全是大于key的值

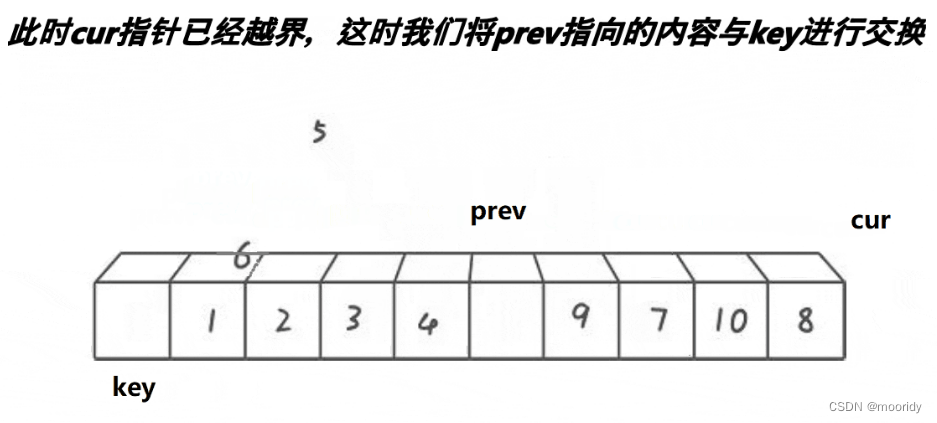
3.當cur越界，將prev指向的內容與key進行呼喚

效果：key左邊的數據都比key小，key右邊的數據都比key大

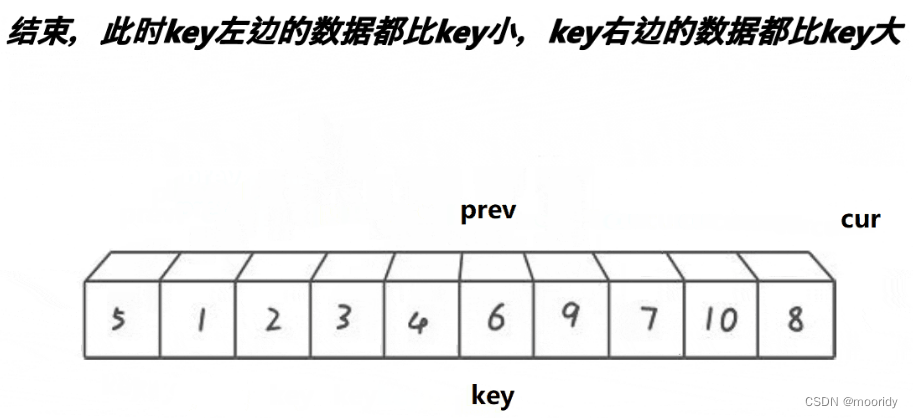
由于快慢指針法單趟后的效果和霍爾法其實是一致的，后續步驟就和霍爾法的步驟一模一樣。

🍎優化：避免自己和自己交換

if (a[cur] < a[key] && ++prev != cur) {//優化：當++prev與cur重疊時，就不進行交換Swap(&a[cur], &a[prev]);}

🥳代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}
//優化1：改變選key的策略，采用三數選中法
int FindMid(int* a, int left, int right) {int mid = (left + right) / 2;if (a[left] < a[right]) {if (a[left] < a[mid]) {if (a[mid] < a[right]) {//a[left]<a[mid]<a[right]return mid;}else {//a[left]<a[right]<a[mid]return right;}}else {//a[mid]<a[left]<a[right]return left;}}else {//a[left] > a[right]if (a[mid] > a[right]) {if (a[mid] > a[left]) {//a[mid] > a[left]> a[right]return left;}else {return mid;}}else {//a[left] > a[right]>a[mid]return right;}}
}void InsertSort(int* a, int n) {for (int i = 1; i < n; i++) {int end = i;int tmp = a[end];while (end > 0) {if (tmp < a[end - 1]) {a[end] = a[end - 1];a[end - 1] = tmp;end--;}else {break;}}}
}void QuickSort2(int* a, int left, int right) {if (left + 5 >= right) {InsertSort(a + left, right - left + 1);return;}//優化：改變選key的策略，采用三數選中法int key = FindMid(a + left, left, right);Swap(&a[left], &a[key]);key = left;int prev = left;int cur = left + 1;while (cur <= right) {if (a[cur] < a[key] && ++prev != cur) {//優化：當++prev與cur重疊時，就不進行交換Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[key], &a[prev]);key = prev;//此時key需要改變QuickSort2(a, left, key - 1);QuickSort2(a, key + 1, right);
}int main(){int a[10] = { 6, 1, 2, 7, 9, 3, 4, 5, 10,8 };QuickSort2(a, 0, 9);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}return 0;
}

🍹非遞歸實現

🍎代碼思路

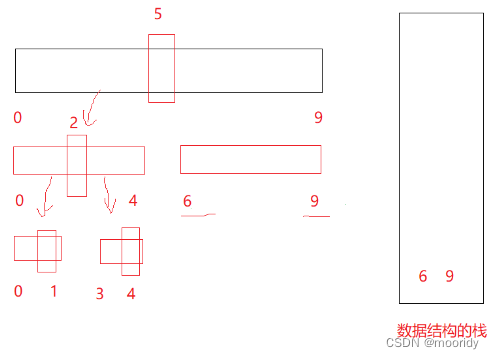
利用棧來模擬遞歸的過程，假設每次key值都剛好二分。

1.初始化一個棧，將right和left壓入棧中

1.對數組進行單趟快速排序，得到[left,key-1],key,[key+1,right]

2.設begin1=left，end1=key-1

? ?設begin2=key+1，end2=right

3.若begin2<end2,將end2，begin2壓入棧中

若begin1<end1,將end1，begin1壓入棧中

4.取并刪除棧頂元素兩次，得到begin1，end1，對[begin1,end1]數組進行單趟快速排序

5.重復步驟2，3,4,棧為空時循環結束

.

🥳代碼實現

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include "stack.h"void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}void QuickSort(int* a, int left, int right) {Stack st;StackInit(&st);StackPush(&st, right);StackPush(&st, left);while (!StackEmpty(&st)) {left = StackTop(&st);StackPop(&st);right = StackTop(&st);StackPop(&st);int begin = left;int end = right;int key = begin;while (begin < end) {while (a[end] >= a[key] && begin < end) {end--;}while (a[begin] <= a[key] && begin < end) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[key]);key = begin;//此時key需要改變int begin1 = left;int end1 = key - 1;int begin2 = key + 1;int end2 = right;if (begin2 < end2) {StackPush(&st, end2);StackPush(&st, begin2);}if (begin1 <end1) {StackPush(&st, end1);StackPush(&st, begin1);}}StackDestroy(&st);return;
}int main() {int a[10] = { 6, 1, 2, 7, 9, 3, 4, 5, 10,8 };QuickSort(a, 0, 9);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}return 0;
}

7.歸并排序

🍹圖解

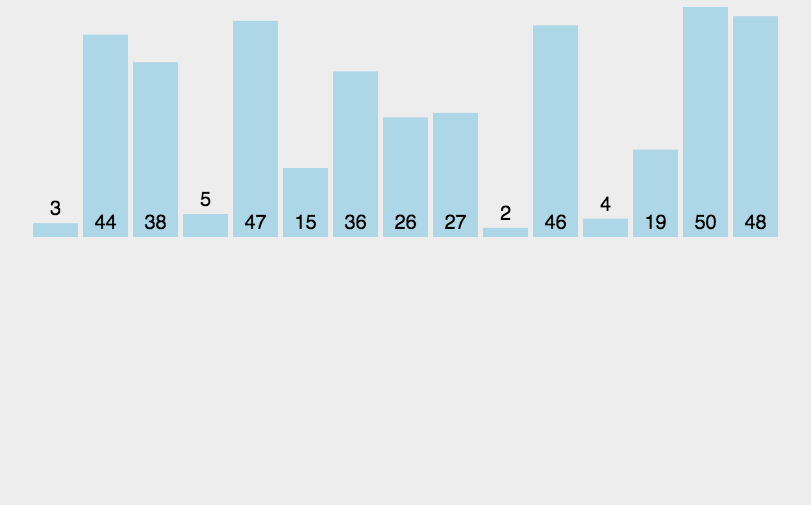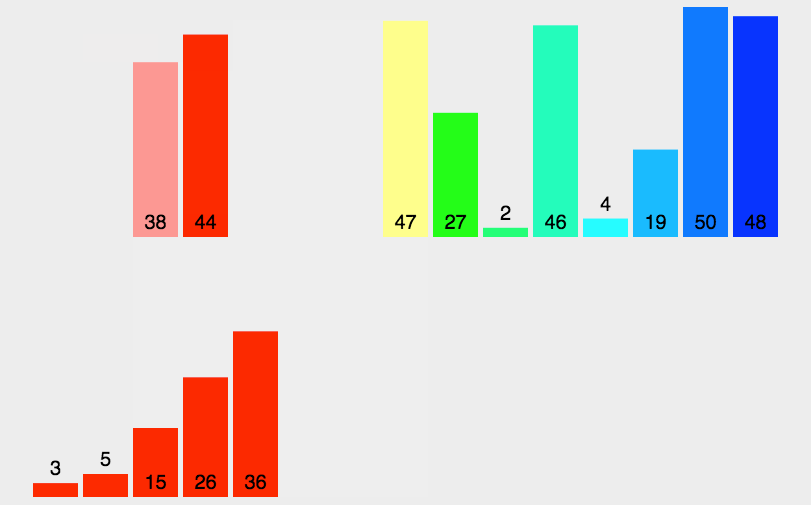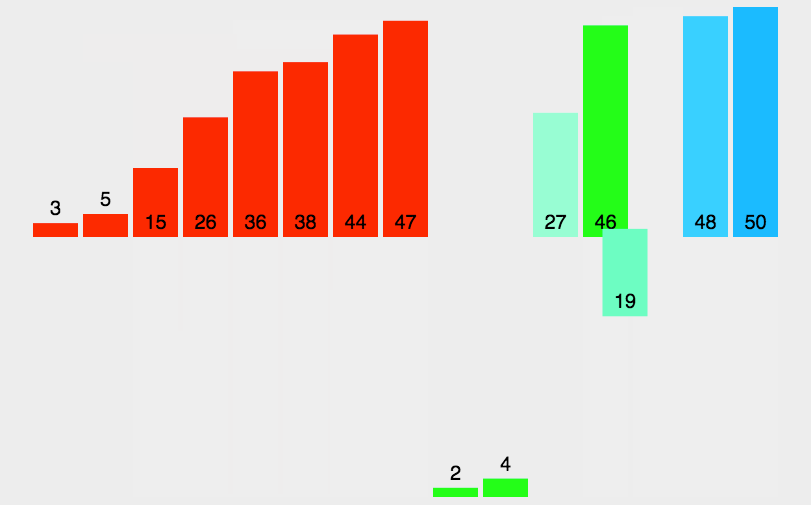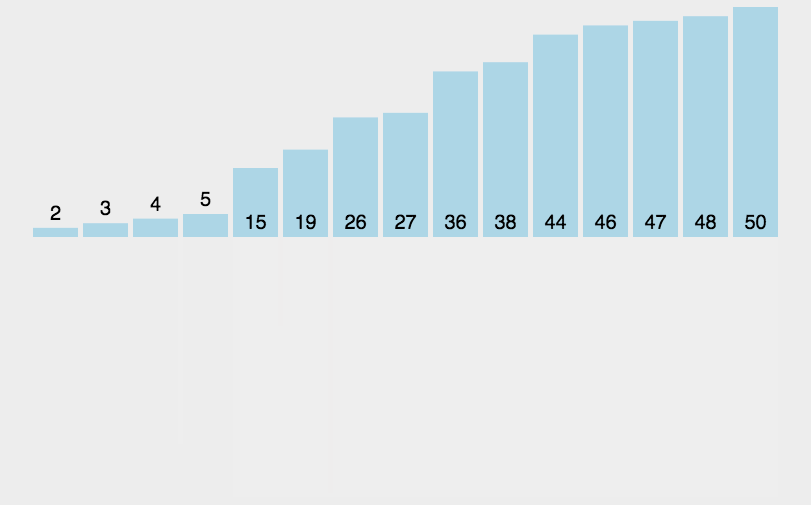
🌴深度剖析

基本思想：
歸并排序（ MERGE-SORT ）是建立在歸并操作上的一種有效的排序算法 , 該算法是采用分治法 。
將已有序的子序列合并，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合并成一個有序表，稱為二路歸并。
歸并排序核心步驟：

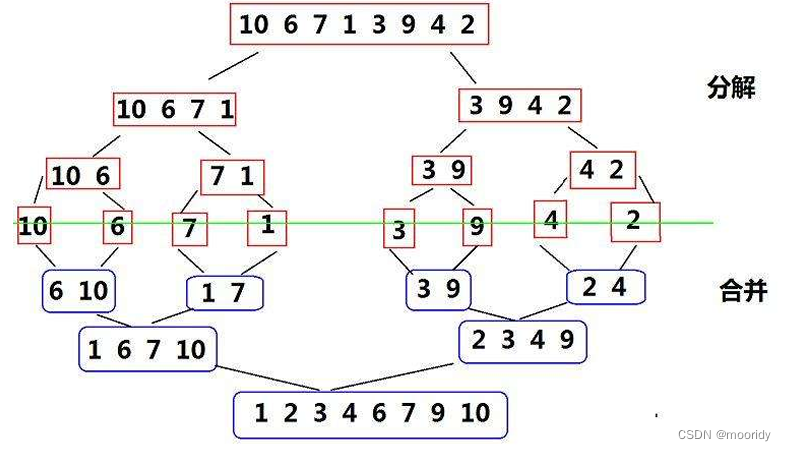
🍹遞歸版

🍎代碼思路

假設數組可以被拆分成兩個子數組：

比較begin1和begin2位置的值，

取小尾插到tmp，

被取指針向前移動

未被取指針，不動

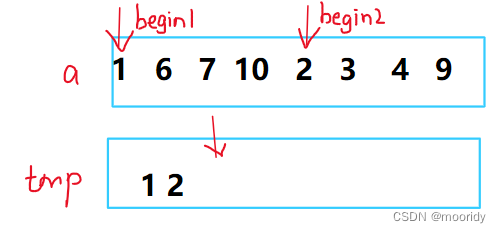
但問題是：數組往往不能直接被拆成兩個有序數組

因此，考慮繼續細分數組直到有序（比如只有1個數時必定有序）

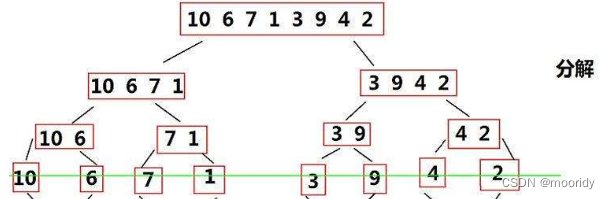
然后將有序子數組一層層的合并回去，每次合并完將結果拷貝回原數組。

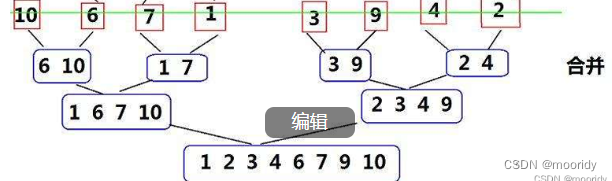
這個過程有點類似后序遍歷。

🥳代碼實現

void MergeSort1(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL) {perror("tmp malloc fail!");return;}if (n <= 1) {//當數組被拆分成單個數，或無法繼續拆分，返回return;}int mid = (n+1)/ 2;//假設數組3個數，mid==2,MergeSort1(a, mid);//[0,mid-1]有序MergeSort1(a+mid, n-mid);//[mid,n-1]有序//合并兩個有序數組int begin1 = 0;int end1 = mid - 1;int begin2 = mid;int end2 = n - 1;int tmp1 = 0;while (begin1 <=end1 && begin2 <= end2) {if (a[begin1] < a[begin2]) {//begin1的數比begin2小，尾插begin1tmp[tmp1] = a[begin1];begin1++;tmp1++;}else {tmp[tmp1] = a[begin2];begin2++;tmp1++;}}//循環結束，說明有一方指針已經走完//將另一方未走完指針走完while (begin1 <=end1) {tmp[tmp1] = a[begin1];begin1++;tmp1++;}while (begin2 <=end2) {tmp[tmp1] = a[begin2];begin2++;tmp1++;}//此時的tmp數組為有序數組//拷貝回原數組memcpy(a, tmp, sizeof(int) * n);
}

🍹非遞歸版

🍎代碼思路

1.首先設一個變量gap代表每組需要歸并的個數。

2.劃分兩個大小為gap的子數組[begin1,end1],[begin2,end2]，這兩個數組應當是有序的，對其進行歸并，歸并完后，繼續向后劃分兩個大小為gap的子數組，繼續歸并，直到整個數組被遍歷完。

3.遍歷完一次數組意味著以gap*2為大小的子數組已經有序，因此gap*=2，以新gap數，繼續完成新一輪對數組的歸并遍歷。直到gap>=2,結束。

🍋思考：上面的思路只能解決數組大小為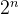2^n的數組，其余數組則會存在越界問題，如何解決？

這是一個數據個數為10的數組：

打印每輪的合并情況，可發現，有些位置發生了越界：

將圖示越界的位置抽象出來，即為：

解決方案：

判斷begin2是否存在，若不存在，則結束歸并，若存在則修正end2，使其不越界。

🥳代碼實現

void MergeSort2(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL) {perror("tmp malloc fail!");return;}if (n <= 1) {//當數組被拆分成單個數，或無法繼續拆分，返回return;}//后序遍歷//合并兩個有序數組int gap = 1;//每組需要歸并的個數while(gap<n){//層序遍歷for(int i=0;i<n;i+=2*gap){int begin1 = i;int end1 = i+gap-1;int begin2 = i+gap;int end2 = i+2*gap-1;int j = i;if (begin2 >= n) {break;}if (end2 >= n) {end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2]) {//begin1的數比begin2小，尾插begin1tmp[j++] = a[begin1];begin1++;}else {tmp[j++] = a[begin2];begin2++;}}//循環結束，說明有一方指針已經走完//將另一方未走完指針走完while (begin1 <= end1) {tmp[j++] = a[begin1];begin1++;}while (begin2 <= end2) {tmp[j++] = a[begin2];begin2++;}//此時的tmp數組為有序數組//拷貝回原數組memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1));//易錯點：(end2-begin1+1)是錯的，因為begin1這個時候已經不再是子數組起點位置}gap *= 2;}}int main() {int a1[8] = { 10,6,7,1,3,9,4,2 };int a2[16] = { 16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1 };int a3[12] = { 12,11,10,9,8,7,6,5,4,3,2,1 };MergeSort2(a1, 8);for (int i = 0; i < 8; i++) {printf("%d ", a1[i]);}printf("\n");MergeSort2(a2, 16);for (int i = 0; i < 16; i++) {printf("%d ", a2[i]);}MergeSort2(a3, 12);printf("\n");for (int i = 0; i < 12; i++) {printf("%d ", a3[i]);}}

🤔時間復雜度

O（N*logN)

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/23323.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/23323.shtml
英文地址，請注明出處：http://en.pswp.cn/web/23323.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

2024 年適用于 Linux 的 5 個微軟 Word 替代品

2024 年適用于 Linux 的 5 個微軟 Word 替代品

對于那些最近由于隱私問題或其他原因而轉向 Linux 的用戶來說&#xff0c;可能很難替換他們最喜歡的、不在 Linux 操作系統上運行的應用程序。 尋找流行程序的合適替代品可能會成為一項挑戰&#xff0c;而且并不是每個人都準備好花費大量時間來嘗試弄清楚什么可以與他們在 Win…
閱讀更多...
讀書筆記|《把自己變成稀缺資產》：我們都擁有100分的欲望，卻只有1分的耐心。

讀書筆記|《把自己變成稀缺資產》：我們都擁有100分的欲望，卻只有1分的耐心。

哈嘍&#xff0c;你好啊&#xff0c;我是雷工&#xff01; 最近在讀一本書《把自己變成稀缺資產》&#xff0c;其中一章講到耐心的重要性&#xff0c;很有共鳴。 當今社會&#xff0c;生活節奏越來越快&#xff0c;我們都在急于求成的追求結果&#xff0c;對過程越來越缺乏耐…
閱讀更多...
C++核心編程友元的應用

C++核心編程友元的應用

文章目錄 1.友元1.什么是友元2.全局函數做友元2.類做友元3.成員函數做友元 1.友元 1.什么是友元 在C中&#xff0c;友元&#xff08;friend&#xff09;是一種允許一個類或函數訪問另一個類的非公有&#xff08;private 或 protected&#xff09;成員的機制。這種機制打破了類…
閱讀更多...
系統研發安全漏洞

系統研發安全漏洞

軟件安全漏洞指的是軟件中存在的具體缺陷或疏忽&#xff0c;這些缺陷或疏忽能夠被攻擊者利用并執行一些惡意行為。這些行為包括但不限于泄露或修改敏感信息、干擾或銷毀系統、接管計算機系統或程序權限等。與大眾熟悉的軟件缺陷&#xff08;Bug&#xff09;相比&#xff0c;安全…
閱讀更多...
Mysql中表的常用約束

Mysql中表的常用約束

在MySQL表中常用的約束有以下幾種&#xff1a; 1. 主鍵約束&#xff08;Primary Key Constraint&#xff09;&#xff1a;用于標識表中的唯一記錄。一個表只能有一個主鍵&#xff0c;主鍵列不能有重復值&#xff0c;也不能為NULL。 2. 唯一約束&#xff08;Unique Constraint…
閱讀更多...
2024050402-重學 Java 設計模式《實戰責任鏈模式》

2024050402-重學 Java 設計模式《實戰責任鏈模式》

重學 Java 設計模式&#xff1a;實戰責任鏈模式「模擬618電商大促期間&#xff0c;項目上線流程多級負責人審批場景」 一、前言 場地和場景的重要性 射擊&#x1f3f9;需要去靶場學習、滑雪&#x1f3c2;需要去雪場體驗、開車&#x1f697;需要能上路實踐&#xff0c;而編程…
閱讀更多...
Scanpy（4）用與數據整合和批次處理

Scanpy（4）用與數據整合和批次處理

Scanpy包，用與數據整合和批次處理，包含批次效應的BBKNN算法和用于對比的ingest基礎算法比較，及其原理簡介。 1. 依賴： （1）數據集（全部需要掛VPN）： PBMC：pbmc3k_processed()（需要下載）；pbmc68k_reduced()（scanpy自帶）Pancreas（需要下載）（2）Python包：Scanp…
閱讀更多...
【Python】把xmind轉換為指定格式txt文本

【Python】把xmind轉換為指定格式txt文本

人工智能訓練通常需要使用文本格式&#xff0c;xmind作為一種常規格式不好進行解析&#xff0c;那如何把xmind轉換為txt格式呢&#xff1f; 軟件信息 python python -v Python 3.9.13 (tags/v3.9.13:6de2ca5, May 17 2022, 16:36:42) [MSC v.1929 64 bit (AMD64)] on win32…
閱讀更多...
Python 包安裝及常用命令【python 入門】

Python 包安裝及常用命令【python 入門】

背景&#xff1a; 近期看到一個項目&#xff0c;做微信只能機器人&#xff0c;服務是使用python搭建的&#xff0c;于是拷貝下來自己打算跑一跑&#xff0c;部署一下&#xff0c;可是自己又沒有python的經驗&#xff0c;于是各種查資料學習&#xff0c;跟著敲一敲&#xff0c;順…
閱讀更多...
Go 1.19.4 切片與子切片-Day 05

Go 1.19.4 切片與子切片-Day 05

1. 切片 1.1 介紹 切片在Go中是一個引用類型&#xff0c;它包含三個組成部分&#xff1a;指向底層數組的指針&#xff08;pointer&#xff09;、切片的長度&#xff08;length&#xff09;以及切片的容量&#xff08;capacity&#xff09;&#xff0c;這些信息共同構成了切片的…
閱讀更多...
單片機排水泵高壓方案

單片機排水泵高壓方案

靈動微多顆算力高、高可靠性的通用系列和電機專用系列MCU&#xff0c;配合成熟的控制算法&#xff0c;覆蓋了包括洗衣機在內的各種大小家電市場。 RAMSUN提供的MM32 MCU種類較多&#xff0c;例如洗衣機內部的排水泵系統&#xff0c;排水泵控制首選電控高性價比產品MM32SPIN023…
閱讀更多...
JavaWeb_SpringBootWeb案例

JavaWeb_SpringBootWeb案例

環境搭建&#xff1a; 開發規范 接口風格-Restful&#xff1a; 統一響應結果-Result&#xff1a; 開發流程&#xff1a; 第一步應該根據需求定義表結構和定義接口文檔 注意&#xff1a; 本文代碼從上往下一直添加功能&#xff0c;后面的模塊下的代碼包括前面的模塊&#xff0c…
閱讀更多...
Xmind Pro 2024 專業版激活碼（附下載鏈接）

Xmind Pro 2024 專業版激活碼（附下載鏈接）

說到思維導圖&#xff0c;就不能不提 Xmind。這是一款優秀的思維導圖工具&#xff0c;擁有著豐富的導圖模板&#xff0c;漂亮的界面和配色&#xff0c;以及各種各樣的創意工具。 新架構速度更快 采用全新 Snowdancer 引擎&#xff0c;一種堪稱「黑科技」的先進圖形渲染技術。…
閱讀更多...
翹首以盼的抗鋸齒

翹首以盼的抗鋸齒

Antialiasing 實際的圖形學中是怎么實現反走樣的呢&#xff1f; 我們不希望實際產出的圖形有鋸齒效果&#xff0c;那怎么辦呢&#xff1f; 從采樣的理論開始談起吧 Simpling theory 照片也是一種采樣&#xff0c;把景象打散成像素放到屏幕上的過程&#xff1a; 還可以在不…
閱讀更多...
14、企業數據資源相關會計處理暫行規定

14、企業數據資源相關會計處理暫行規定

為規范企業數據資源相關會計處理， 強化相關會計信息披露， 根據《中華人民共和國會計法》 和企業會計準則等相關規定， 現對企業數據資源的相關會計處理規定如下： 一、 關于適用范圍 本規定適用于企業按照企業會計準則相關規定確認為無形資產或存貨等資產類別的數據資源，以…
閱讀更多...
21 - 即時食物配送 II（高頻 SQL 50 題基礎版)

21 - 即時食物配送 II（高頻 SQL 50 題基礎版)

21 - 即時食物配送 II -- sum(if(order_datecustomer_pref_delivery_date,1,0))/count(*)sum(order_datecustomer_pref_delivery_date)/count(*) -- count(*),表示數據的行數&#xff0c;如果有分組&#xff0c;為分組后數據的行數select round(100*sum(if(order_datecustomer_…
閱讀更多...
【名詞解釋】Unity的Button組件及其使用示例

【名詞解釋】Unity的Button組件及其使用示例

Unity的Button組件是Unity引擎中UI系統的一部分&#xff0c;它允許用戶創建可交互的按鈕&#xff0c;用戶可以點擊這些按鈕來觸發事件。Button組件通常用于游戲界面中&#xff0c;比如開始游戲、暫停游戲、選擇選項等。 Button組件的主要屬性包括&#xff1a; interactable: …
閱讀更多...
原來Stable Diffusion是這樣工作的

原來Stable Diffusion是這樣工作的

stable diffusion是一種潛在擴散模型&#xff0c;可以從文本生成人工智能圖像。為什么叫做潛在擴散模型呢&#xff1f;這是因為與在高維圖像空間中操作不同&#xff0c;它首先將圖像壓縮到潛在空間中&#xff0c;然后再進行操作。 在這篇文章中&#xff0c;我們將深入了解它到…
閱讀更多...
達摩院重大“遺產”！fluxonium量子比特初始化300納秒且保真度超過99%

達摩院重大“遺產”！fluxonium量子比特初始化300納秒且保真度超過99%

通用量子計算機開發的主要挑戰之一是制備量子比特。十多年來&#xff0c;研究人員在構建量子計算機的過程中主要使用了transmon量子比特&#xff0c;這也是迄今為止商業上最成功的超導量子比特。 但與業界多數選擇transmon量子比特不同&#xff0c;&#xff08;前&#xff09;…
閱讀更多...
npm運行報錯：無法加載文件 C:\Program Files\nodejs\npm.ps1，因為在此系統上禁止運行腳本問題解決

npm運行報錯：無法加載文件 C:\Program Files\nodejs\npm.ps1，因為在此系統上禁止運行腳本問題解決

問題其實已經顯而易見了 系統禁止運行腳本 以管理員身份運行 PowerShell&#xff1a; 右鍵點擊“開始”按鈕或按 Win X&#xff0c;然后選擇“Windows PowerShell(管理員)”。 查看當前執行策略&#xff1a; 在 PowerShell 中輸入以下命令來查看當前的執行策略&#xff1a; G…
閱讀更多...
最新文章

Copyright @ 2022~2023