論文地址:https://arxiv.org/pdf/2405.04434
相關博客
【自然語言處理】【大模型】DeepSeek-V2論文解析
【自然語言處理】【大模型】BitNet:用1-bit Transformer訓練LLM
【自然語言處理】BitNet b1.58:1bit LLM時代
【自然語言處理】【長文本處理】RMT:能處理長度超過一百萬token的Transformer
【自然語言處理】【大模型】MPT模型結構源碼解析(單機版)
【自然語言處理】【大模型】ChatGLM-6B模型結構代碼解析(單機版)
【自然語言處理】【大模型】BLOOM模型結構源碼解析(單機版)
一、簡介
- DeepSeek-V2是一個總參數為236B的MoE模型,每個token僅激活21B的參數,并支持128K的上下文長度。
- 提出了Multi-head Latent Attention(MLA),通過壓縮kv cache至隱向量,從而保證高效推理。
- 相比于DeepSeek 67B,DeepSeek-V2實現了更好的表現,節約了42.5%的訓練成本,降低了93.3%的kv cache,提升最大吞吐5.76倍。
- 預訓練語料包含了8.1T tokens并進一步進行SFT和RL。
二、模型結構
1. MLA(Multi-Head Latent Attention)
? 傳統Transformer采用MHA(Multi-Head Attention),但是kv cache會成為推理瓶頸。MQA(Multi-Query Attention)和GQA(Grouped-Query Attention)可以一定程度減少kv cache,但效果上不如MHA。DeepSeek-V2設計了一種稱為MLA(Multi-Head Latent Attention)的注意力機制。MLA通過低秩key-value聯合壓縮,實現了比MHA更好的效果并且需要的kv cache要小很多。
1.1 標準MHA
? 令 d d d為embedding維度, n h n_h nh?是注意力頭的數量, d h d_h dh?是每個頭的維度, h t ∈ R d \textbf{h}_t\in\mathbb{R}^d ht?∈Rd是注意力層中第 t t t個token的輸入。標準MHA通過三個矩陣 W Q , W K , W V ∈ R d h n h × d W^Q,W^K,W^V\in\mathbb{R}^{d_h n_h\times d} WQ,WK,WV∈Rdh?nh?×d來產生 q t , k t , v t ∈ R d h n h \textbf{q}_t,\textbf{k}_t,\textbf{v}_t\in\mathbb{R}^{d_h n_h} qt?,kt?,vt?∈Rdh?nh?。
q t = W Q h t k t = W K h t v t = W V h t \begin{align} \textbf{q}_t&=W^Q\textbf{h}_t \tag{1}\\ \textbf{k}_t&=W^K\textbf{h}_t \tag{2}\\ \textbf{v}_t&=W^V\textbf{h}_t \tag{3}\\ \end{align} \\ qt?kt?vt??=WQht?=WKht?=WVht??(1)(2)(3)?
在MHA中 q t , k t , v t \textbf{q}_t,\textbf{k}_t,\textbf{v}_t qt?,kt?,vt?會被劃分為 n h n_h nh?個頭:
[ q t , 1 ; q t , 2 ; … , q t , n h ] = q t [ k t , 1 ; k t , 2 ; … , k t , n h ] = k t [ v t , 1 ; v t , 2 ; … , v t , n h ] = v t o t , i = ∑ j = 1 t Softmax ( q t , i ? k j , i d h ) v j , i u t = W O [ o t , 1 ; o t , 2 ; … , o t , n h ] \begin{align} &[\textbf{q}_{t,1};\textbf{q}_{t,2};\dots,\textbf{q}_{t,n_h}]=\textbf{q}_t \tag{4}\\ &[\textbf{k}_{t,1};\textbf{k}_{t,2};\dots,\textbf{k}_{t,n_h}]=\textbf{k}_t \tag{5}\\ &[\textbf{v}_{t,1};\textbf{v}_{t,2};\dots,\textbf{v}_{t,n_h}]=\textbf{v}_t \tag{6}\\ &\textbf{o}_{t,i}=\sum_{j=1}^t\text{Softmax}(\frac{\textbf{q}_{t,i}^\top\textbf{k}_{j,i}}{\sqrt{d_h}})\textbf{v}_{j,i} \tag{7}\\ &\textbf{u}_t=W^O[\textbf{o}_{t,1};\textbf{o}_{t,2};\dots,\textbf{o}_{t,n_h}] \tag{8}\\ \end{align} \\ ?[qt,1?;qt,2?;…,qt,nh??]=qt?[kt,1?;kt,2?;…,kt,nh??]=kt?[vt,1?;vt,2?;…,vt,nh??]=vt?ot,i?=j=1∑t?Softmax(dh??qt,i??kj,i??)vj,i?ut?=WO[ot,1?;ot,2?;…,ot,nh??]?(4)(5)(6)(7)(8)?
其中 q t , i , k t , i , v t , i ∈ R d h \textbf{q}_{t,i},\textbf{k}_{t,i},\textbf{v}_{t,i}\in\mathbb{R}^{d_h} qt,i?,kt,i?,vt,i?∈Rdh?是第 i i i個注意力頭的query、key和value, W O ∈ R d × d h n h W^O\in\mathbb{R}^{d\times d_h n_h} WO∈Rd×dh?nh?是輸出投影矩陣。在推理時,所有的key和value都會被緩存來加速推理。對于每個token,MHA需要緩存 2 n h d h l 2n_h d_h l 2nh?dh?l個元素。
1.2 低秩Key-Value聯合壓縮

? MLA通過低秩聯合壓縮key和value來減少kv cache:
c t K V = W D K V h t k t C = W U K c t K V v t C = W U V c t K V \begin{align} \textbf{c}_t^{KV}&=W^{DKV}\textbf{h}_t \tag{9}\\ \textbf{k}_t^C&=W^{UK}\textbf{c}_t^{KV} \tag{10}\\ \textbf{v}_t^C&=W^{UV}\textbf{c}_t^{KV} \tag{11}\\ \end{align} \\ ctKV?ktC?vtC??=WDKVht?=WUKctKV?=WUVctKV??(9)(10)(11)?
其中 c t K V ∈ R d c \textbf{c}_t^{KV}\in\mathbb{R}^{d_c} ctKV?∈Rdc?是用于壓縮key和value的隱向量; d c ( ? d h n h ) d_c(\ll d_h n_h) dc?(?dh?nh?)表示KV壓縮的維度; W D K V ∈ R d c × d W^{DKV}\in\mathbb{R}^{d_c\times d} WDKV∈Rdc?×d是下投影矩陣, W U K , W U V ∈ R d h n h × d c W^{UK},W^{UV}\in\mathbb{R}^{d_h n_h\times d_c} WUK,WUV∈Rdh?nh?×dc?表示上投影矩陣。在推理時,MLA僅需要緩存 c t K V \textbf{c}_t^{KV} ctKV?,因此kv cache僅需要緩存 d c l d_c l dc?l個元素。此外,在推理時可以把 W U K W^{UK} WUK吸收到 W Q W^Q WQ, W U V W^{UV} WUV吸收到 W O W^O WO中,這樣甚至都不需要計算key和value。
關于推理時權重融合的理解:
? 這里不考慮具體注意力頭,僅就單個頭進行分析。先來分析 q t ? k j C \textbf{q}_t^\top\textbf{k}_j^C qt??kjC?,
q t ? k j C = ( W Q h t ) ? W U K c j K V = h t ? W Q ? W U K c j K V = h t ? W Q U K c j K V \begin{align} \textbf{q}_t^\top\textbf{k}_j^C&=(W^Q\textbf{h}_t)^\top W^{UK}\textbf{c}_j^{KV} \\ &=\textbf{h}_t^\top {W^Q}^\top W^{UK} \textbf{c}_j^{KV} \\ &=\textbf{h}_t^\top W^{QUK} \textbf{c}_j^{KV} \\ \end{align} \\ qt??kjC??=(WQht?)?WUKcjKV?=ht??WQ?WUKcjKV?=ht??WQUKcjKV???
推理時可以將 W Q ? W U K {W^Q}^\top W^{UK} WQ?WUK預先計算出來,記為 W Q U K W^{QUK} WQUK。再來看整個注意力輸出值的計算過程
u t = W O o t = W O ∑ j = 1 t Softmax j ( q t ? k j d h ) v j = W O ∑ j = 1 t Softmax j ( q t ? k j d h ) W U V c j K V = W O W U V ∑ j = 1 t Softmax j ( q t ? k j d h ) c j K V = W O U V ∑ j = 1 t Softmax j ( q t ? k j d h ) c j K V \begin{align} \textbf{u}_t&=W^O\textbf{o}_t \\ &=W^O\sum_{j=1}^t\text{Softmax}_j(\frac{\textbf{q}_t^\top\textbf{k}_j}{\sqrt{d_h}})\textbf{v}_j \\ &=W^O\sum_{j=1}^t\text{Softmax}_j(\frac{\textbf{q}_t^\top\textbf{k}_j}{\sqrt{d_h}})W^{UV}\textbf{c}_j^{KV} \\ &=W^OW^{UV}\sum_{j=1}^t\text{Softmax}_j(\frac{\textbf{q}_t^\top\textbf{k}_j}{\sqrt{d_h}})\textbf{c}_j^{KV} \\ &=W^{OUV}\sum_{j=1}^t\text{Softmax}_j(\frac{\textbf{q}_t^\top\textbf{k}_j}{\sqrt{d_h}})\textbf{c}_j^{KV} \\ \end{align} \\ ut??=WOot?=WOj=1∑t?Softmaxj?(dh??qt??kj??)vj?=WOj=1∑t?Softmaxj?(dh??qt??kj??)WUVcjKV?=WOWUVj=1∑t?Softmaxj?(dh??qt??kj??)cjKV?=WOUVj=1∑t?Softmaxj?(dh??qt??kj??)cjKV???
W O W U V W^O W^{UV} WOWUV的結果記為 W O U V W^{OUV} WOUV。通過這樣的方式就不需要顯式計算key和value。
? 此外,為了在訓練時降低激活的顯存占用,對query也進行低秩壓縮,即使其不能降低kv cache。具體來說,
c t Q = W D Q h t q t C = W U Q c t Q \begin{align} \textbf{c}_t^Q&=W^{DQ}\textbf{h}_t \tag{12}\\ \textbf{q}_t^C&=W^{UQ}\textbf{c}_t^Q \tag{13} \\ \end{align} \\ ctQ?qtC??=WDQht?=WUQctQ??(12)(13)?
其中 c t Q ∈ R d c ′ \textbf{c}_t^Q\in\mathbb{R}^{d_c'} ctQ?∈Rdc′?是query的壓縮后隱向量; d c ′ ( ? d h n h ) d_c'(\ll d_h n_h) dc′?(?dh?nh?)表示query的壓縮維度; W D Q ∈ R d c ′ × d , W U Q ∈ R d h n h × d c ′ W^{DQ}\in\mathbb{R}^{d_c'\times d},W^{UQ}\in\mathbb{R}^{d_h n_h\times d_c'} WDQ∈Rdc′?×d,WUQ∈Rdh?nh?×dc′?是下投影矩陣和上投影矩陣。
1.3 解耦RoPE
? RoPE與低秩KV壓縮并不兼容。具體來說,RoPE對于query和key是位置敏感的。若將RoPE應用在 k t C \textbf{k}_t^C ktC?上,等式10中的 W U K W^{UK} WUK將與位置敏感RoPE矩陣耦合。但是在推理時, W U K W^{UK} WUK就無法被吸收到 W Q W^Q WQ中,因為對當前生成token相關的RoPE矩陣將位于 W Q W^Q WQ和 W U K W^{UK} WUK之間,而矩陣乘法不滿足交換律。因此,推理時必須重新計算前面token的key,這會顯著影響推理效率。
關于RoPE與抵秩KV壓縮不兼容的理解。
RoPE向 k t C \textbf{k}_t^C ktC?注入位置信息的方式為 f ( k t C , t ) = R t k t C f(\textbf{k}_t^C,t)=R_t\textbf{k}_t^C f(ktC?,t)=Rt?ktC?,其中 R t R_t Rt?是一個位置敏感的矩陣。那么有
q t ? f ( k j C , j ) = ( W Q h t ) ? R j W U K c j K V = h t ? W Q ? R j W U K c j K V \begin{align} \textbf{q}_t^\top f(\textbf{k}_j^C,j)&=(W^Q\textbf{h}_t)^\top R_j W^{UK}\textbf{c}_j^{KV} \\ &=\textbf{h}_t^\top {W^Q}^\top R_j W^{UK} \textbf{c}_j^{KV} \\ \end{align} \\ qt??f(kjC?,j)?=(WQht?)?Rj?WUKcjKV?=ht??WQ?Rj?WUKcjKV???
由于 R j R_j Rj?是未知敏感的,導致 W Q ? R j W U K {W^Q}^\top R_j W^{UK} WQ?Rj?WUK針對不同的token,取值不一樣。無法像先前那樣直接融合為 W Q U K W^{QUK} WQUK。
? 為了解決這個問題,提出使用額外的多頭query q t , i R ∈ R d h R \textbf{q}_{t,i}^R\in\mathbb{R}^{d_h^R} qt,iR?∈RdhR?和共享key k t R ∈ R d h R \textbf{k}_t^R\in\mathbb{R}^{d_h^R} ktR?∈RdhR?來攜帶RoPE,其中 d h R d_h^R dhR?表示解耦query和key的每個頭的維度。在MLA中使用解耦RoPE策略的方式為:
q t R = [ q t , 1 R ; q t , 2 R ; … ; q t , n h R ] = RoPE ( W Q R c t Q ) k t R = RoPE ( W K R h t ) q t , i = [ q t , i C ; q t , i R ] k t , i = [ k t , i C ; k t R ] o t , i = ∑ j = 1 t Softmax j ( q t , i ? k j , i d h + d h R ) v j , i C u t = W O [ o t , 1 ; o t , 2 ; … ; o t , n h ] \begin{align} \textbf{q}_t^R&=[\textbf{q}_{t,1}^R;\textbf{q}_{t,2}^R;\dots;\textbf{q}_{t,n_h}^R]=\text{RoPE}(W^{QR}\textbf{c}_t^Q) \tag{14}\\ \textbf{k}_t^R&=\text{RoPE}(W^{KR}\textbf{h}_t) \tag{15}\\ \textbf{q}_{t,i}&=[\textbf{q}_{t,i}^C;\textbf{q}_{t,i}^R] \tag{16}\\ \textbf{k}_{t,i}&=[\textbf{k}_{t,i}^C;\textbf{k}_t^R] \tag{17} \\ \textbf{o}_{t,i}&=\sum_{j=1}^t\text{Softmax}_j(\frac{\textbf{q}_{t,i}^\top\textbf{k}_{j,i}}{\sqrt{d_h+d_h^R}})\textbf{v}_{j,i}^C \tag{18} \\ \textbf{u}_t&=W^O[\textbf{o}_{t,1};\textbf{o}_{t,2};\dots;\textbf{o}_{t,n_h}] \tag{19}\\ \end{align} \\ qtR?ktR?qt,i?kt,i?ot,i?ut??=[qt,1R?;qt,2R?;…;qt,nh?R?]=RoPE(WQRctQ?)=RoPE(WKRht?)=[qt,iC?;qt,iR?]=[kt,iC?;ktR?]=j=1∑t?Softmaxj?(dh?+dhR??qt,i??kj,i??)vj,iC?=WO[ot,1?;ot,2?;…;ot,nh??]?(14)(15)(16)(17)(18)(19)?
其中 W Q R ∈ R d h R n h × d c ′ W^{QR}\in\mathbb{R}^{d_h^R n_h\times d_c'} WQR∈RdhR?nh?×dc′?和 W K R ∈ R d h R × d W^{KR}\in\mathbb{R}^{d_h^R\times d} WKR∈RdhR?×d是用于產生解耦query和key的矩陣; RoPE ( ? ) \text{RoPE}(\cdot) RoPE(?)表示應用RoPE的操作; [ ? ; ? ] [\cdot;\cdot] [?;?]表示拼接操作。在推理時,解耦的key也需要被緩存。因此,DeekSeek-V2需要的總kv cache包含 ( d c + d h R ) l (d_c+d_h^R)l (dc?+dhR?)l個元素。
1.4 結論
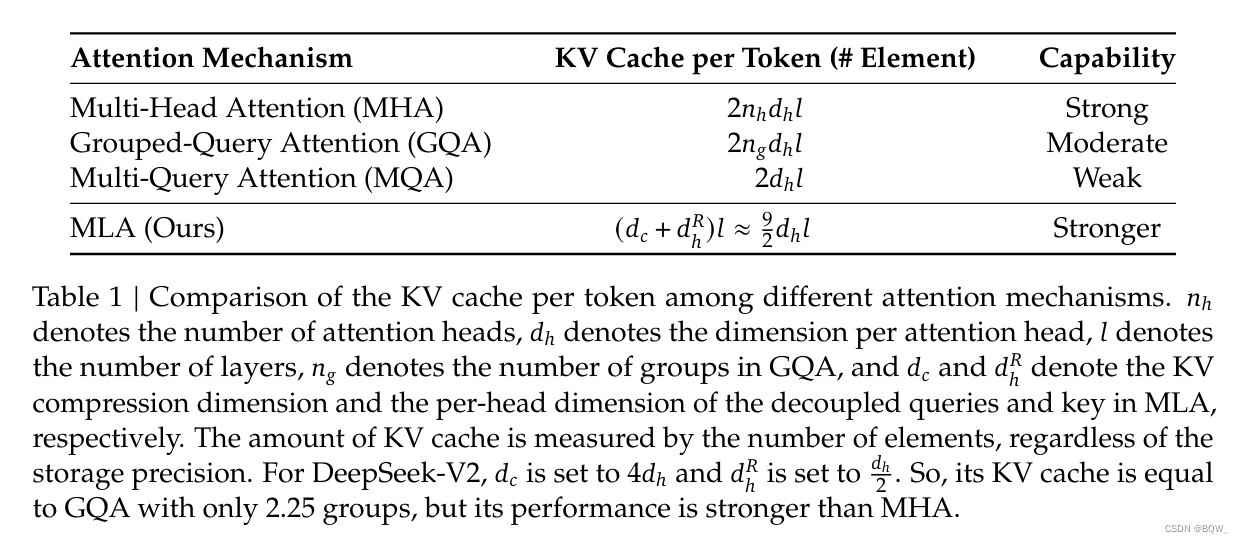
? MLA能夠通過更少的kv cache實現比MHA更好的效果。
2. 整體結構
2.1 基礎結構
? 對于FFN層,利用DeepSeekMoE架構,即將專家劃分為更細粒度,從而獲得更專業化的專家以及獲取更準確的知識。在具有相同激活和總專家參數的情況下,DeepSeekMoE能夠大幅度超越傳統MoE架構。
? 令 u t \textbf{u}_t ut?是第t個token對FFN的輸入,那么計算FFN的輸出 h t ′ \textbf{h}_t' ht′?為:
h t ′ = u t + ∑ i = 1 N s FFN i ( s ) ( u t ) + ∑ i = 1 N r g i , t FFN i ( r ) ( u t ) g i , t = { s i , t , s i , t ∈ Topk ( { s j , t ∣ 1 ≤ j ≤ N r } , K r ) 0 , otherwise s i , t = Softmax i ( u t ? e i ) \begin{align} \textbf{h}_t'&=\textbf{u}_t+\sum_{i=1}^{N_s}\text{FFN}_i^{(s)}(\textbf{u}_t)+\sum_{i=1}^{N_r}g_{i,t}\text{FFN}_{i}^{(r)}(\textbf{u}_t) \tag{20}\\ g_{i,t}&=\begin{cases} s_{i,t},& s_{i,t}\in\text{Topk}(\{s_{j,t}|1\leq j\leq N_r\},K_r)\\ 0,&\text{otherwise} \end{cases}\tag{21}\\ s_{i,t}&=\text{Softmax}_i(\textbf{u}_t^\top \textbf{e}_i) \tag{22}\\ \end{align} \\ ht′?gi,t?si,t??=ut?+i=1∑Ns??FFNi(s)?(ut?)+i=1∑Nr??gi,t?FFNi(r)?(ut?)={si,t?,0,?si,t?∈Topk({sj,t?∣1≤j≤Nr?},Kr?)otherwise?=Softmaxi?(ut??ei?)?(20)(21)(22)?
其中 N s N_s Ns?和 N r N_r Nr?表示共享專家和路由專家的數量; FFN i ( s ) ( ? ) \text{FFN}_i^{(s)}(\cdot) FFNi(s)?(?)和 FFN i ( r ) ( ? ) \text{FFN}_i^{(r)}(\cdot) FFNi(r)?(?)表示第i個共享專家和第i個路由專家; K r K_r Kr?表示激活路由專家的數量; g i , t g_{i,t} gi,t?是第i個專家的門限值; e i \textbf{e}_i ei?是當前層第i個路由專家的中心。
2.2 設備受限路由
? 設計了一種設備受限路由機制來控制MoE相關的通信成本。當采用專家并行時,路由專家將分布在多個設備上。對于每個token,MoE相關的通信頻率與目標專家覆蓋的設備數量成正比。由于在DeepSeekMoE中細粒度專家劃分,激活專家的數量會很大,因此應用專家并行時,與MoE相關的通信將更加昂貴。
? 對于DeepSeek-V2,除了路由專家會選擇top-K個以外,還會確保每個token的目標專家最多分布在M個設備上。具體來說,對于每個token,先選擇包含最高分數專家的M個設備。然后在這M個設備上執行top-K選擇。在實踐中,當 M ≥ 3 M\geq 3 M≥3時,設備受限路由能夠實現與不受限top-K路由大致一致的良好性能。
2.3 用于負載均衡的輔助loss
? 不平衡的負載會增加路由坍縮的風險,使一些專家無法得到充分的訓練和利用。此外,當使用專家并行時,不平衡的負載降低計算效率。在DeepSeek-V2訓練時,設計了三種輔助損失函數用于控制專家級別負載均衡 ( L ExpBal ) (\mathcal{L}_{\text{ExpBal}}) (LExpBal?)、設備級別負載均衡 ( L DevBal ) (\mathcal{L}_{\text{DevBal}}) (LDevBal?)和通信均衡 L CommBal \mathcal{L}_{\text{CommBal}} LCommBal?。
? 專家級均衡loss。專家級均衡loss用于緩解路由坍縮問題:
L ExpBal = α 1 ∑ i = 1 N r f i P i , f i = N r K r T ∑ t = 1 T 1 (Token?t?selects?Expert?i) P i = 1 T ∑ t = 1 T s i , t \begin{align} \mathcal{L}_{\text{ExpBal}}&=\alpha_1\sum_{i=1}^{N_r}f_iP_i, \tag{23} \\ f_i&=\frac{N_r}{K_r T}\sum_{t=1}^T\mathbb{1}\text{(Token t selects Expert i)} \tag{24} \\ P_i&=\frac{1}{T}\sum_{t=1}^T s_{i,t} \tag{25} \\ \end{align} \\ LExpBal?fi?Pi??=α1?i=1∑Nr??fi?Pi?,=Kr?TNr??t=1∑T?1(Token?t?selects?Expert?i)=T1?t=1∑T?si,t??(23)(24)(25)?
其中 α 1 \alpha_1 α1?是稱為專家級均衡因子的超參數; 1 ( ? ) \mathbb{1}(\cdot) 1(?)是指示函數; T T T是序列中token的數量。
? 設備級均衡loss。除了專家級均衡loss以外,也設計了設備級別均衡loss來確保跨設備均衡計算。在DeepSeek-V2訓練過程中,將所有的專家劃分至 D D D組 { E 1 , E 2 , … , E D } \{\mathcal{E}_1,\mathcal{E}_2,\dots,\mathcal{E}_D\} {E1?,E2?,…,ED?}并在單個設備上部署每個組。設備級均衡loss計算如下:
L DevBal = α 2 ∑ i = 1 D f i ′ P i ′ f i ′ = 1 E i ∑ j ∈ E i f j P i ′ = ∑ j ∈ E i P j \begin{align} \mathcal{L}_{\text{DevBal}}&=\alpha_2\sum_{i=1}^D f_i' P_i'\tag{26} \\ f_i'&=\frac{1}{\mathcal{E}_i}\sum_{j\in\mathcal{E}_i}f_j \tag{27} \\ P_i'&=\sum_{j\in\mathcal{E}_i}P_j \tag{28} \\ \end{align} \\ LDevBal?fi′?Pi′??=α2?i=1∑D?fi′?Pi′?=Ei?1?j∈Ei?∑?fj?=j∈Ei?∑?Pj??(26)(27)(28)?
其中 α 2 \alpha_2 α2?是稱為設備級均衡因子的超參數。
? 通信均衡loss。通信均衡loss能夠確保每個設備通信的均衡。雖然設備限制路由機制能夠確保每個設備發送信息有上限,但是當某個設備比其他設備接收更多的tokens,那么實際通信效率將會有影響。為了緩解這個問題,設計了一種通信均衡loss如下:
L CommBal = α 3 ∑ t = 1 D f i ′ ′ P i ′ ′ f i ′ ′ = D M T ∑ t = 1 T 1 (Token?t?is?sent?to?Device?i) P i ′ ′ = ∑ j ∈ E i P j \begin{align} \mathcal{L}_{\text{CommBal}}&=\alpha_3\sum_{t=1}^D f_i''P_i''\tag{29} \\ f_i''&=\frac{D}{MT}\sum_{t=1}^T\mathbb{1}\text{(Token t is sent to Device i)}\tag{30} \\ P_i''&=\sum_{j\in\mathcal{E}_i}P_j\tag{31} \\ \end{align} \\ LCommBal?fi′′?Pi′′??=α3?t=1∑D?fi′′?Pi′′?=MTD?t=1∑T?1(Token?t?is?sent?to?Device?i)=j∈Ei?∑?Pj??(29)(30)(31)?
其中 α 3 \alpha_3 α3?是稱為通信均衡因子的超參數。設備受限路由機制操作主要確保每個設備至多向其他設備傳輸MT個hidden states。同時,通信均衡loss用來鼓勵每個設備從其他設備接受MT個hidden states。通信均衡loss確保設備間信息均衡交換,實現高效通信。
2.4 Token-Dropping策略
? 雖然均衡loss的目標是確保均衡負載,但是其并不能嚴格確保負載均衡。為了進一步緩解由于不均衡導致的計算浪費,在訓練時引入了設備級別的token-dropping策略。該方法會先計算每個設備的平均計算預算,這意味著每個設備的容量因子等于1.0。然而,在每個設備上drop具有最低affinity分數的token,直到達到計算預算。此外,確保大約10%的訓練序列的token永遠不會被drop。這樣,可以根據效率要求靈活地決定是否在推理過程中drop token,并確保訓練和推理的一致性。
三、預訓練
1. 實驗設置
1.1 數據構造
? 數據處理過程同DeepSeek 67B,并進一步擴展數據量和質量。采用與DeepSeek 67B相同的tokenizer。預訓練語料包含8.1T tokens,中文token比英文多12%。
1.2 超參數
? 略
1.3 Infrastructures
? DeepSeek-V2訓練基于HAI-LLM框架。利用16路0氣泡流水并行、8路專家并行和ZeRO-1數據并行。考慮到DeepSeek-V2具有相對較少的激活參數,并且對一部分操作進行重計算來節約激活顯存,因此可以不使用張量并行,從而降低通信開銷。此外,為了進一步提高訓練效率,使用專家并行all-to-all通信來重疊共享專家的計算。使用定制化的CUDA核來改善通信、路由算法和不同專家之間融合線性計算。此外,MLA基于改善版本的FlashAttention-2進行優化。
1.4 長上下文擴展
? 使用YaRN將上下文窗口尺寸從4K擴展至128K。
2. 評估
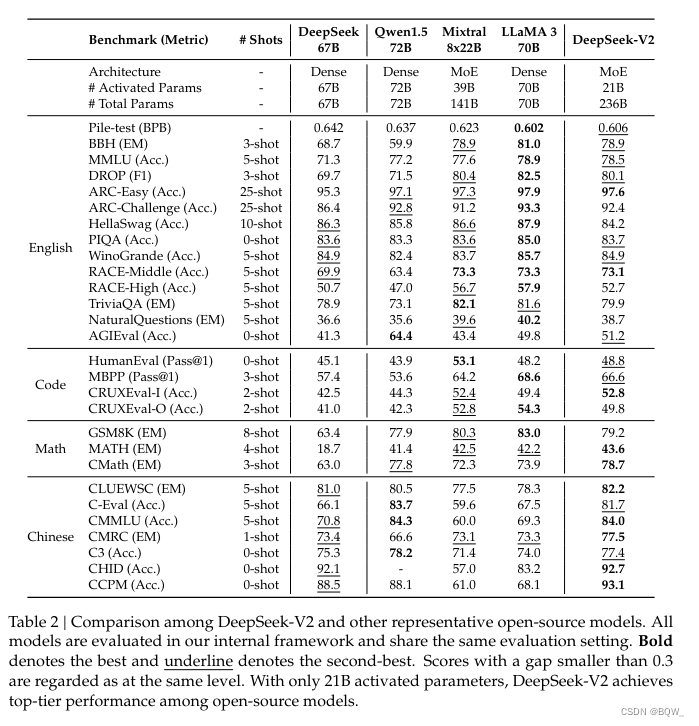
四、對齊
? SFT。 使用了150萬樣本的微調數據,其中120萬是用于有用性,30萬則用于安全性。
? 強化學習。仍然采用GRPO。
? 結果。
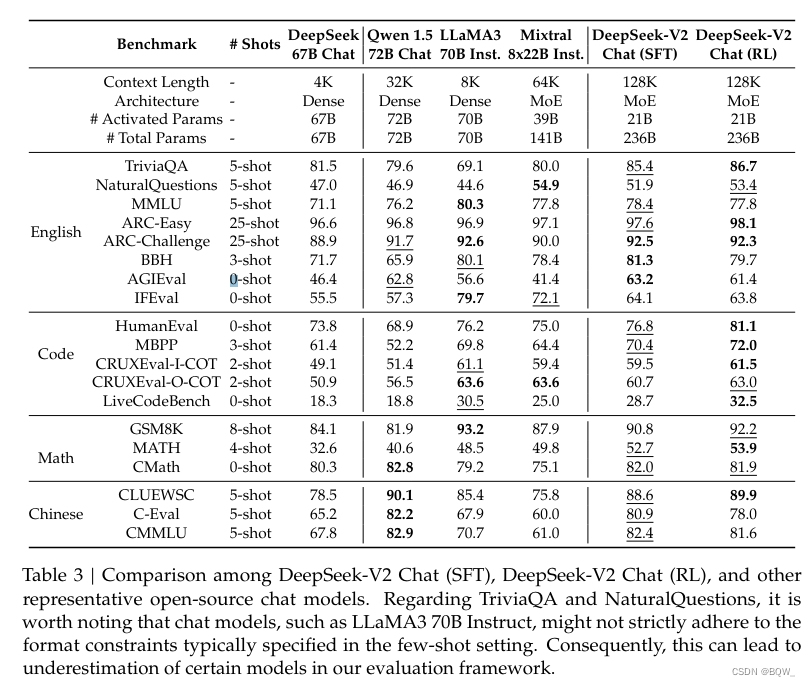



表達式語言(EL)的隱式對象及其作用)


如何學習OMXNodeInstance)
)

:區間DP)




)


 - 用 C 語言自定義命令)
