動態規劃----股票買賣問題（詳解）

目錄

一.買賣股票的最佳時機：

二.買賣股票的最佳時機含冷凍期：

三.買賣股票的最佳時期含?續費：

四.買賣股票的最佳時機III:?

五.買賣股票的最佳時機IV:

買賣股票的最佳時機問題介紹：動態規劃買賣股票的最佳時機是一個經典的算法問題。該問題的目標是在給定的股票價格數組中，找到最大的利潤，即最佳的買入和賣出時間，使得買入時間早于賣出時間。

下面我們通過一些例題，來解決這一類動態規劃的問題：

一.買賣股票的最佳時機：

  • 題目鏈接：121. 買賣股票的最佳時機 - 力扣（LeetCode）
  • 題目描述：

    給定一個數組?prices?，它的第?i?個元素?prices[i]?表示一支給定股票第?i?天的價格。

    你只能選擇?某一天?買入這只股票，并選擇在?未來的某一個不同的日子?賣出該股票。設計一個算法來計算你所能獲取的最大利潤。

    返回你可以從這筆交易中獲取的最大利潤。如果你不能獲取任何利潤，返回?0?。

①.動態規劃解法：

  • 一.狀態表示dp[ i ][ j ]：下標為?i?這一天結束的時候，手上持股狀態為?j?時，我們持有的最大利潤。這里我們定義狀態 j （兩種情況）分別為：
  • 0?買入狀態
  • 1?可交易狀態
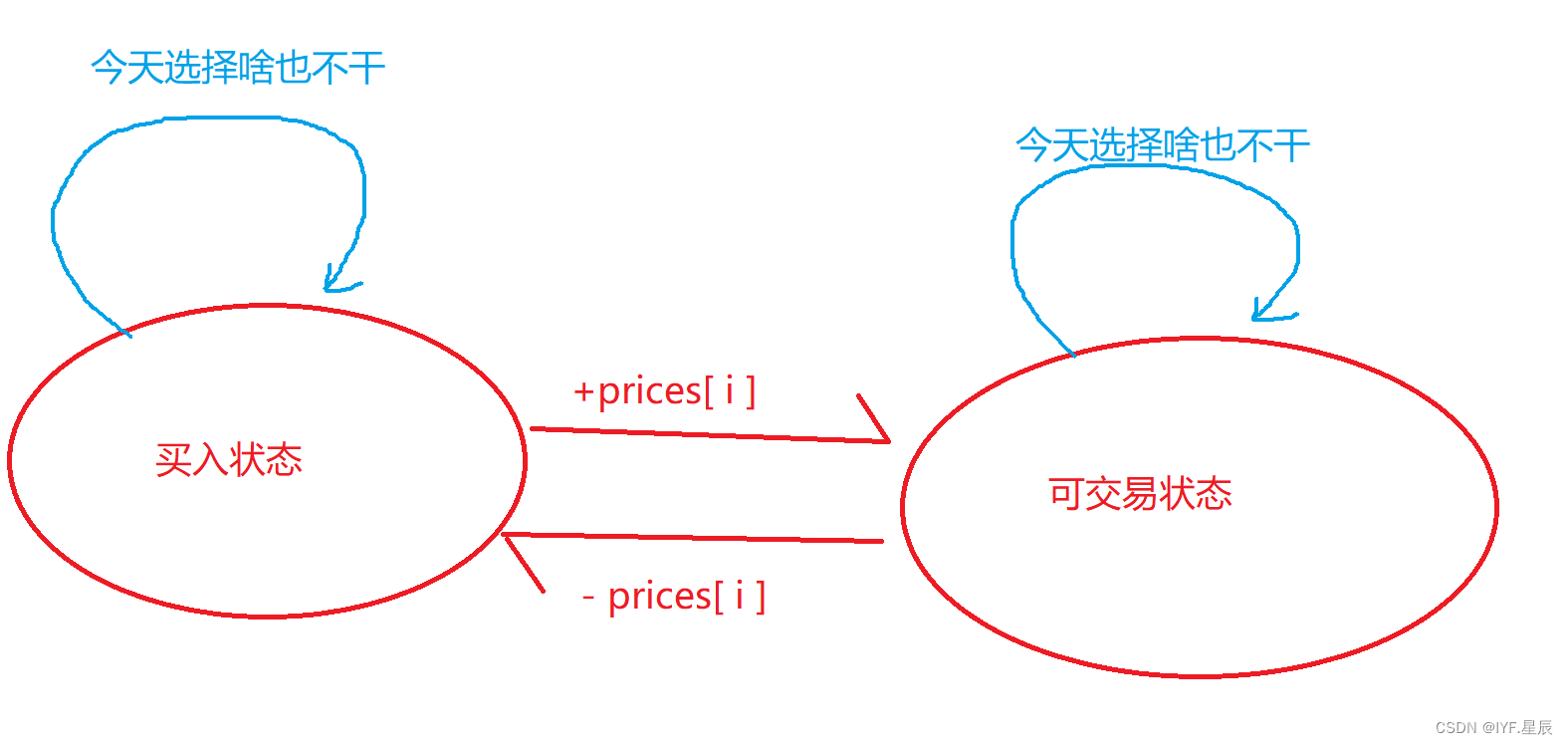
  • 二.狀態轉移方程：
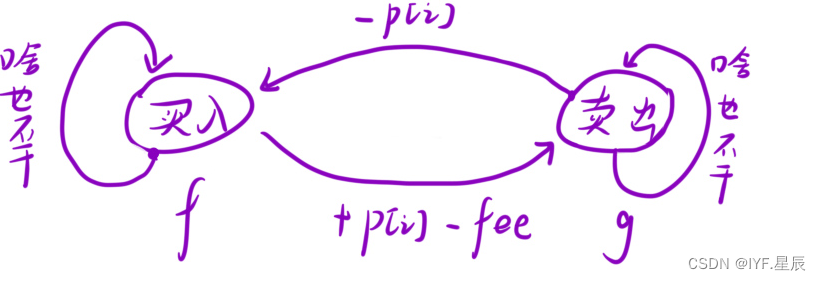
  • dp[ i ][ 0 ] = Math.max( dp[ i - 1 ][ 0 ], -prices[ i ]) ; ①.在前面一天已經是買入狀態，今天選擇什么也不干，今天結束后，是買入狀態。②.前面是可交易狀態，今天選擇買入，則今天結束后是買入狀態，這里注意不是dp[ i - 1][ 1 ] - prices[ i ];因為只能交易一次，如果今天選擇買入，那后面一定要賣出（這算一次交易),此時才可能有最大利潤。則前面不能有交易，利潤為0.
  • dp[ i ][ 1 ] = Math.max( dp[ i - 1][ 1 ],dp[ i - 1][ 0 ] + prices[ i ]);①.前面一天是可交易狀態，今天選擇什么也不干，今天結束后是可交易狀態。②.前面一天是買入狀態，今天選擇賣出，今天結束后是可交易狀態。
  • 三.初始化：根據狀態表示：
  • dp[ 0 ][ 0 ] = - prices[ 0 ];第一天選擇買入，此時利潤為 - prices[ 0 ]
  • dp[ 0 ][ 1 ] = 0;第一天選擇什么也不干或則交易一次，此時的利潤為0;
  • 四.填表順序：根據狀態轉移方程，從左往右，從上往下填寫.
  • 五.返回值：dp[ n - 1 ][ 1 ];n為prices數組的長度,最后一天結束后，是可交易狀態，此時為最大利潤.

各個狀態關系圖：

代碼詳解：

class Solution {// 1. 創建 dp 表// 2. 初始化// 3. 填表// 4. 返回值public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][2];//初始化dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1;i < n;i++){//注意這里不是dp[i - 1][1] - prices[i];dp[i][0] = Math.max(dp[i - 1][0], - prices[i]);dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] + prices[i]);}//返回值return dp[n - 1][1];}
}

②.暴力解法（相對簡單這里給出解題過程）：?

代碼詳解：

class Solution {public int maxProfit(int[] prices) {int cost = Integer.MAX_VALUE;int profit = 0;for(int price : prices){cost = Math.min(cost,price);profit = Math.max(profit,price - cost);}return profit;}
}

運行結果：

?

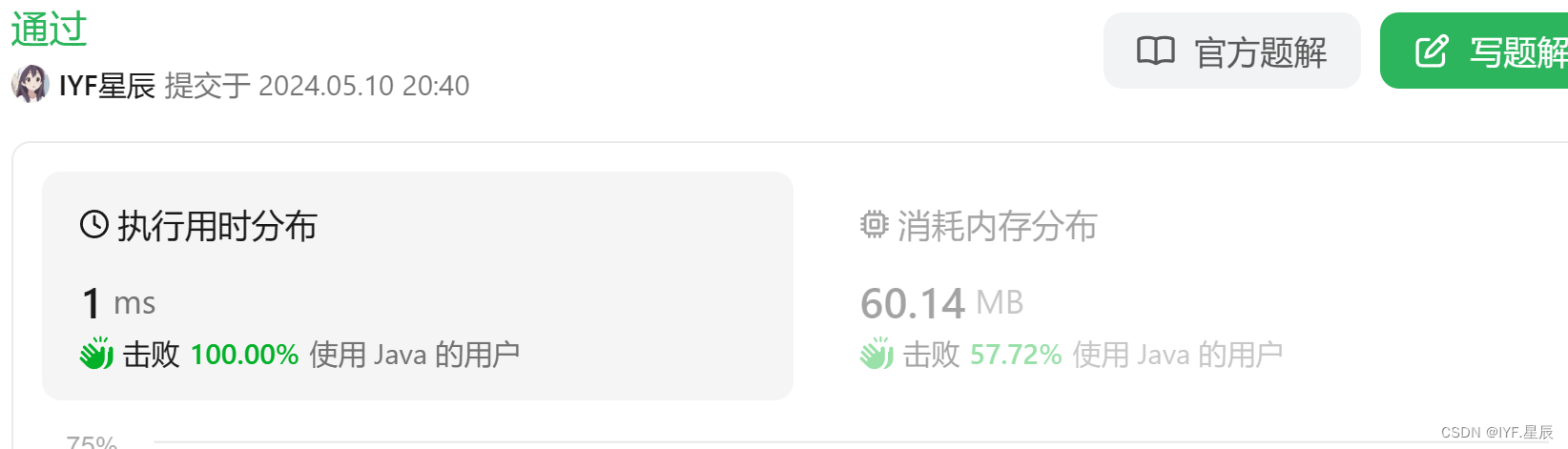二.買賣股票的最佳時機含冷凍期：

  • 題目鏈接：309. 買賣股票的最佳時機含冷凍期 - 力扣（LeetCode）
  • 問題描述：

    給定一個整數數組prices，其中第??prices[i]?表示第?i?天的股票價格 。?

    設計一個算法計算出最大利潤。在滿足以下約束條件下，你可以盡可能地完成更多的交易（多次買賣一支股票）:

  • 賣出股票后，你無法在第二天買入股票 (即冷凍期為 1 天)。

  • 注意：你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。

動態規劃解法：

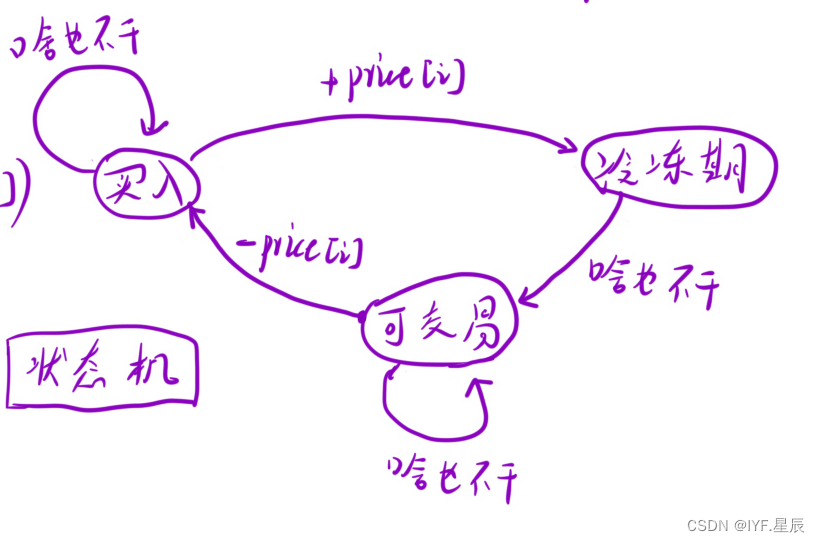
一.狀態表示：dp[ i ][ j ]:由于有「買?」「可交易」「冷凍期」三個狀態，因此我們可以選擇?三個數組，其中：

  • dp[i][0] 表?：第 i 天結束后，處于「買?」狀態，此時的最?利潤；
  • dp[i][1] 表?：第 i 天結束后，處于「可交易」狀態，此時的最?利潤；
  • dp[i][2] 表?：第 i 天結束后，處于「冷凍期」狀態，此時的最?利潤

二.狀態轉移方程：

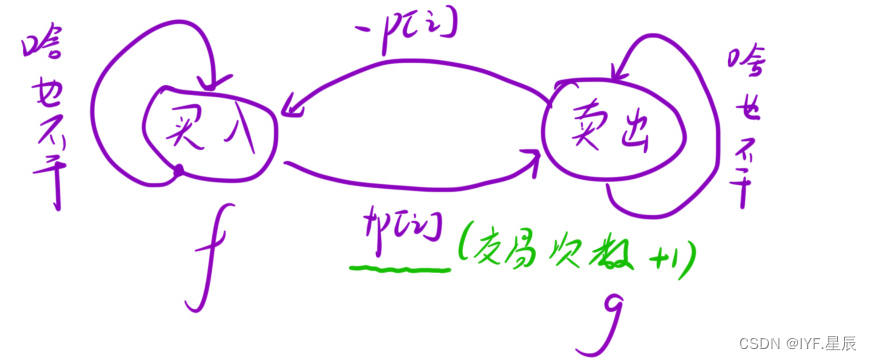
  • dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); ①.前一天是買入狀態，今天啥也不做，今天結束后是買入狀態②.前面一天是可交易狀態，今天選擇買入，今天結束后是買入狀態。
  • dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]); ①.前面一天是可交易狀態，今天啥也不干，今天結束后是可交易狀態②.前面一天是冷凍期，今天啥也不干，今天過后是可交易狀態
  • dp[i][2] = dp[i - 1][0] + prices[i]；前面一天是買入狀態，今天選擇賣出，今天過后是冷凍期

三.初始化：

dp[0][0] = - prices[0] ；? ?dp[0][1] = 0 ；? ? dp[0][2] = 0;

四.填表順序：從左往右，從上往下，依次填寫三個表

五.返回值：狀態轉移方程三者的最大值：

?max(dp[n - 1][1], dp[n - 1] [2]);dp[n - 1][0]不可能是最大值，這里不用考慮進去（如果考慮進去了也沒關系）

各個狀態關系圖：

代碼詳解：

class Solution {// 1. 創建 dp 表// 2. 初始化// 3. 填表// 4. 返回值public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][3];dp[0][0] = -prices[0];for(int i = 1;i < n;i++){dp[i][0] = Math.max(dp[i - 1][0],dp[i - 1][1] - prices[i]);dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}return Math.max(dp[n - 1][1],dp[n - 1][2]);}
}

運行結果：?

三.買賣股票的最佳時期含?續費：

題目鏈接：714. 買賣股票的最佳時機含手續費 - 力扣（LeetCode）

題目描述：

給定一個整數數組?prices，其中?prices[i]表示第?i?天的股票價格 ；整數?fee?代表了交易股票的手續費用。

你可以無限次地完成交易，但是你每筆交易都需要付手續費。如果你已經購買了一個股票，在賣出它之前你就不能再繼續購買股票了。

返回獲得利潤的最大值。

注意：這里的一筆交易指買入持有并賣出股票的整個過程，每筆交易你只需要為支付一次手續費。

?動態規劃解法：

一.狀態表示：由于有「買?」「可交易」兩個狀態，因此我們可以選擇?兩個數組來定義我們的狀態（或則一個二維數組也行），其中：

  • f[i] 表?：第 i 天結束后，處于「買?」狀態，此時的最?利潤；
  • g[i] 表?：第 i 天結束后，處于「賣出」狀態，此時的最?利潤.

二.狀態轉移方程 ：我們選擇在「賣出」的時候，?付這個?續費，那么在「買?」的時候，就不?再考慮?續費的問題（完成一次交易支付手續費）：

  • f[i] = max(f[i - 1], g[i - 1] - prices[i]) ；①.在 i - 1 天「持有」股票，第 i 天啥也不?。此時最?收益為 f[i - 1] ；②.在 i - 1 天的時候「沒有」股票，在第 i 天買?股票。此時最?收益為 g[i - 1] - prices[i]) ；
  • g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee);①.在 i - 1 天「持有」股票，但是在第 i 天將股票賣出。此時最?收益為： f[i - 1] + prices[i] - fee) ，記得?續費；②.在 i - 1 天「沒有」股票，然后第 i 天啥也不?。此時最?收益為： g[i - 1]

三.初始化：由于需要?到前?的狀態，因此需要初始化第?個位置:

  • 對于 f[0] ，此時處于「買?」狀態，因此 f[0] = -prices[0]
  • 對于 g[0] ，此時處于「沒有股票」狀態，啥也不?即可獲得最?收益，因此 g[0] = 0?

四.填表順序：從左到右兩個表一起填

五.返回值：應該返回「賣出」狀態下，最后?天的最?值收益： g[n - 1]?

代碼詳解：

class Solution {public int maxProfit(int[] prices, int fee) {int n = prices.length;int[] f = new int[n];int[] g = new int[n];f[0] = -prices[0];for(int i = 1;i < n;i++){f[i] = Math.max(f[i - 1],g[i - 1] - prices[i]);g[i] = Math.max(g[i - 1],f[i - 1] + prices[i] - fee);}return Math.max(f[n - 1],g[n - 1]);}
}

運行結果：

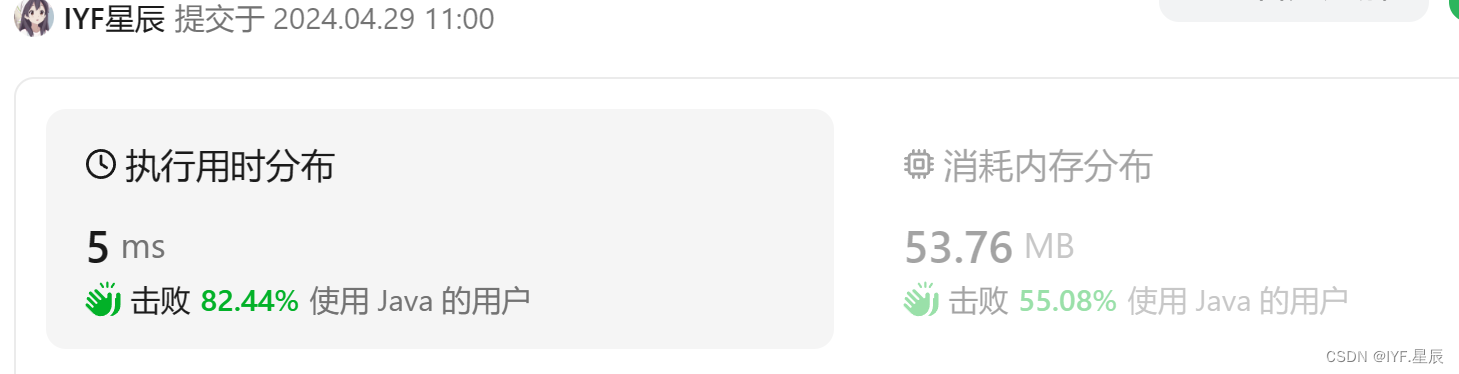
四.買賣股票的最佳時機III:?

題目鏈接：123. 買賣股票的最佳時機 III - 力扣（LeetCode）

題目描述：

給定一個數組，它的第?i?個元素是一支給定的股票在第?i?天的價格。

設計一個算法來計算你所能獲取的最大利潤。你最多可以完成?兩筆?交易。

注意：你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。

動態規劃解法：

一.狀態表示：由于有「買?」「可交易」兩個狀態，因此我們可以選擇?兩個數組。但是這道題??還有交易次 數的限制，因此我們還需要再加上?維，?來表?交易次數。其中：

  • f[i][j] 表?：第 i 天結束后，完成了 j 次交易，處于「買?」狀態，此時的最?利 潤；
  • g[i][j] 表?：第 i 天結束后，完成了 j 次交易，處于「賣出」狀態，此時的最?利 潤。

二.狀態轉移方程：

  • f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);①.在 i - 1 天的時候，交易了 j 次，處于「買?」狀態，第 i 天啥也不?即可。此時最 ?利潤為： f[i - 1][j] ；②.在 i - 1 天的時候，交易了 j 次，處于「賣出」狀態，第 i 天的時候把股票買了。此 時的最?利潤為： g[i - 1][j] - prices[i] 。
  • g[i][j] = g[i - 1][j];

? ? ? if(j >?0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);??

? ? ?①.在 i - 1 天的時候，交易了 j 次，處于「賣出」狀態，第 i 天啥也不?即可。此時的 最? ? ? ? ? ? ??利潤為： g[i - 1][j] ；

? ? ②.在 i - 1 天的時候，交易了 j - 1 次，處于「買?」狀態，第 i 天把股票賣了，然 后就完? ? ? ? ? 成了 j ?交易。此時的最?利潤為： f[i - 1][j - 1] + prices[i] 。但 是這個狀態不?定存? ? ? ? ? ? ? 在，要先判斷?下。

三.初始化：

  • 當處于第 0 天的時候，只能處于「買?過?次」的狀態，此時的收益為 -prices[0] ，因 此 f[0][0] = - prices[0] 。
  • 為了取 max 的時候，?些不存在的狀態「起不到?擾」的作?，我們統統將它們初始化為 - INF （? INT_MIN 在計算過程中會有「溢出」的?險，這? INF 折半取 0x3f3f3f3f ，?夠?即可）

四.填表順序：從「上往下填」每??，每??「從左往右」，兩個表「?起填」。

五.返回值：返回處于「賣出狀態」的最?值，但是我們也「不知道是交易了?次」，因此返回 g 表最后?? 的最?值。

代碼詳解：

class Solution {static int INF = -0x3f3f3f3f;public int maxProfit(int[] prices) {int n = prices.length;int[][] f = new int[n][3];int[][] g = new int[n][3];//1.f[0][0] = -prices[0];for(int i = 1;i < f[0].length;i++){f[0][i] = INF;}for(int j = 1;j < g[0].length;j++){g[0][j] = INF;//Integer.MIN_VALUE/2}//2.for(int i = 1;i < n;i++){for(int j = 0;j < 3;j++){f[i][j] = Math.max(f[i - 1][j],g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j > 0){g[i][j] = Math.max(g[i][j],f[i - 1][j - 1] + prices[i]);}}}int res = Integer.MIN_VALUE;for(int j = 0;j < 3;j++){ res = Math.max(res,g[n - 1][j]);}return res;}
}

運行結果：

五.買賣股票的最佳時機IV:

題目鏈接：188. 買賣股票的最佳時機 IV - 力扣（LeetCode）

題目描述：

給你一個整數數組?prices?和一個整數?k?，其中?prices[i]?是某支給定的股票在第?i?天的價格。

設計一個算法來計算你所能獲取的最大利潤。你最多可以完成?k?筆交易。也就是說，你最多可以買?k?次，賣?k?次。

注意：你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。

動態規劃解法：

一.狀態表示：為了更加清晰的區分「買?」和「賣出」，我們換成「有股票」和「?股票」兩個狀態：

  • f[i][j] 表?：第 i 天結束后，完成了 j 筆交易，此時處于「有股票」狀態的最?收益；
  • g[i][j] 表?：第 i 天結束后，完成了 j 筆交易，此時處于「?股票」狀態的最?收益

二.狀態轉移方程：

  • f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);①.在 i - 1 天的時候，??「有股票」，并且交易了 j 次。在第 i 天的時候，啥也不?。 此時的收益為 f[i - 1][j] ；②.在 i - 1 天的時候，??「沒有股票」，并且交易了 j 次。在第 i 天的時候，買了股 票。那么 i 天結束之后，我們就有股票了。此時的收益為 g[i - 1][j] - prices[i];
  • g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);①.在 i - 1 天的時候，??「沒有股票」，并且交易了 j 次。在第 i 天的時候，啥也不 ?。此時的收益為 g[i - 1][j] ；②.在 i - 1 天的時候，??「有股票」，并且交易了 j - 1 次。在第 i 天的時候，把 股票賣了。那么 i 天結束之后，我們就交易了 j 次。此時的收益為 f[i - 1][j - 1] + prices[i] ；

三.初始化：

  • 當處于第 0 天的時候，只能處于「買?過?次」的狀態，此時的收益為 -prices[0] ，因 此 f[0][0] = - prices[0]
  • 為了取 max 的時候，?些不存在的狀態「起不到?擾」的作?，我們統統將它們初始化為 - INF （? INT_MIN 在計算過程中會有「溢出」的?險，這? INF 折半取 0x3f3f3f3f ，?夠?即可）

四.填表順序：從上往下填每??，每??從左往右，兩個表?起填。

五.返回值：返回處于賣出狀態的最?值，但是我們也不知道是交易了?次，因此返回 g 表最后??的最? 值

代碼詳解：

class Solution {static int INF = -0x3f3f3f3f;public int maxProfit(int k, int[] prices) {int n = prices.length;int[][] f = new int[n][k + 1];int[][] g = new int[n][k + 1];//1.f[0][0] = -prices[0];for(int i = 1;i < f[0].length;i++){f[0][i] = INF;//->防止越界g[i - 1][j] - prices[i];}for(int j = 1;j < g[0].length;j++){g[0][j] = INF;//Integer.MIN_VALUE/2}//2.for(int i = 1;i < n;i++){for(int j = 0;j < k + 1;j++){f[i][j] = Math.max(f[i - 1][j],g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j > 0){g[i][j] = Math.max(g[i][j],f[i - 1][j - 1] + prices[i]);}}}int res = Integer.MIN_VALUE;for(int j = 0;j < k + 1;j++){ res = Math.max(res,g[n - 1][j]);}return res;}
}

運行結果：

?結語：?寫博客不僅僅是為了分享學習經歷，同時這也有利于我鞏固知識點，總結該知識點，由于作者水平有限，對文章有任何問題的還請指出，接受大家的批評，讓我改進。同時也希望讀者們不吝嗇你們的點贊+收藏+關注，你們的鼓勵是我創作的最大動力！

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/10732.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/10732.shtml
英文地址，請注明出處：http://en.pswp.cn/web/10732.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

windows使用Docker-Desktop部署lobe-chat

windows使用Docker-Desktop部署lobe-chat

文章目錄 window安裝docker-desktop下載和啟動lobe-chatAI大語言模型的選擇lobe-chat設置大模型連接 window安裝docker-desktop docker-desktop下載地址 正常安裝應用&#xff0c;然后啟動應用&#xff0c;注意啟動docker引擎 打開右上角的設置&#xff0c;進入Docker Engine設…
閱讀更多...
算法學習系列（六十）：區間DP

算法學習系列（六十）：區間DP

目錄 引言區間合并模板一、石子合并二、環形石子合并三、能量項鏈 引言 關于這個區間 D P DP DP &#xff0c;其實是有套路和模板的&#xff0c;題型的話也是變化不多&#xff0c;感覺就那幾種&#xff0c;只不過有些題會用到高精度或者是要記錄方案&#xff0c;所以整體來說…
閱讀更多...
Unity編輯器如何多開同一個項目？

Unity編輯器如何多開同一個項目？

在聯網游戲的開發過程中&#xff0c;多開客戶端進行聯調是再常見不過的需求。但是Unity并不支持編輯器多開同一個項目&#xff0c;每次都得項目打個包(耗時2分鐘以上)&#xff0c;然后編輯器開一個進程&#xff0c;exe 再開一個&#xff0c;真的有夠XX的。o(╥﹏╥)o沒錯&#…
閱讀更多...
Hive 與 SQL 標準和主流 SQL DB 的語法區別

Hive 與 SQL 標準和主流 SQL DB 的語法區別

文章目錄 1.Hive 簡介2.Hive 與 SQL 標準和主流 SQL DB 的語法區別參考文獻 1.Hive 簡介 Hive是一種基于Hadoop的數據倉庫軟件&#xff0c;可以將結構化數據文件映射為一張數據庫表&#xff0c;并提供了類SQL查詢接口&#xff0c;使得用戶可以使用SQL類語言來查詢數據。Hive可…
閱讀更多...
7-117 死亡隧道

7-117 死亡隧道

小毛驢要回家了，憑借著剛從老毛驢處學到的閃爍魔法，小毛驢信心滿滿地出發了。這一次它來到了另一條死亡隧道口，但是，小毛驢不知道死亡威脅隨時存在，因為它所打算穿過的這條死亡隧道即將于T秒時間后坍塌。 已知小毛驢行走的速度是每秒17米，而小毛驢擁有的閃爍法術可以使它…
閱讀更多...
返回類型后置，一個用途是為了邏輯上的體現？

返回類型后置，一個用途是為了邏輯上的體現？

大家一般都是先關心參數&#xff0c;然后最后再看返回的是什么類型。 在這里把返回類型后置&#xff0c;可能就是一種邏輯上的體現吧 fmt的一個函數。 \fmt\core.h 這個函數的意義&#xff0c;應該就是用變長參數初始化成一個format_arg_store類型的變量&#xff0c;并返回。…
閱讀更多...
Rust學習筆記（上）

Rust學習筆記（上）

前言 筆記的內容主要參考與《Rust 程序設計語言》&#xff0c;一些也參考了《通過例子學 Rust》和《Rust語言圣經》。 Rust學習筆記分為上中下&#xff0c;其它兩個地址在Rust學習筆記&#xff08;中&#xff09;和Rust學習筆記&#xff08;下&#xff09;。 編譯與運行 Ru…
閱讀更多...
成功解決No module named ‘huggingface_hub.inference._text_generation‘

成功解決No module named ‘huggingface_hub.inference._text_generation‘

成功解決No module named huggingface_hub.inference._text_generation 目錄 解決問題 解決思路 解決方法 解決問題 No module named huggingface_hub.inferen
閱讀更多...
python使用yaml文件以及元組樣式字符串使用eval的類型轉換

python使用yaml文件以及元組樣式字符串使用eval的類型轉換

編程中&#xff0c;對于可變內容&#xff0c;最好是將其放入配置文件中&#xff0c;經過這段時間的學習&#xff0c;感覺使用yaml文件很方便。我的環境&#xff1a;win10&#xff0c;python3.8.10。 python使用yaml文件&#xff0c;首先要安裝庫。 pip38 install pyyaml 安裝…
閱讀更多...
AWTK 開源串口屏開發(18) - 用 C 語言自定義命令

AWTK 開源串口屏開發(18) - 用 C 語言自定義命令

AWTK-HMI 內置了不少模型&#xff0c;利用這些模型開發應用程序&#xff0c;不需要編寫代碼即可實現常見的應用。但是&#xff0c;有時候我們需要自定義一些命令&#xff0c;以實現一些特殊的功能。 本文檔介紹如何使用 C 語言自定義命令。 1. 實現 hmi_model_cmd_t 接口 1.1…
閱讀更多...
實現二叉樹的基本操作

實現二叉樹的基本操作

博主主頁: 碼農派大星. 關注博主帶你了解更多數據結構知識 1我們先來模擬創建一個二叉樹 public class TestBinaryTreee {static class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val val;}}public TreeNode …
閱讀更多...
交叉編譯u-boot,qemu啟動測試

交叉編譯u-boot,qemu啟動測試

交叉編譯u-boot 1 配置交叉編譯工具鏈&#xff1a; 下載地址 https://releases.linaro.org/components/toolchain/binaries/ ### CROSS-COMPILE export AARCH64_LINUX_GNU_TOOLS/media/wmx/cross_compile_tools/aarch64-linux-gun/gcc-x86_64_aarch64-linux-gnu/bin export …
閱讀更多...
linux 安裝 mangodb 并設置服務開機自啟

linux 安裝 mangodb 并設置服務開機自啟

1、下載 wget http://mosquitto.org/files/source/mosquitto-1.6.8.tar.gz 2、解壓 tar -zxvf mosquitto-1.6.8.tar.gz 3、編譯安裝cd mosquitto-1.6.8 make sudo make install4、在當前目錄。進入mosquitto服務文件存放的文件夾 cd service/systemd可以看到3個文件 點擊read…
閱讀更多...
【C/C++】設計模式——工廠模式：簡單工廠、工廠方法、抽象工廠

【C/C++】設計模式——工廠模式：簡單工廠、工廠方法、抽象工廠

創作不易&#xff0c;本篇文章如果幫助到了你&#xff0c;還請點贊 關注支持一下?>&#x16966;<)!! 主頁專欄有更多知識&#xff0c;如有疑問歡迎大家指正討論&#xff0c;共同進步&#xff01; &#x1f525;c系列專欄&#xff1a;C/C零基礎到精通 &#x1f525; 給大…
閱讀更多...
二.基礎篇: 面向對象進階

二.基礎篇: 面向對象進階

1. 基礎篇語法篇&#xff1a;一.基礎篇&#xff1a;基礎語法-CSDN博客 面向對象進階 本章主要學習內容&#xff1a; static繼承包&#xff0c;final&#xff0c;權限修飾符&#xff0c;代碼塊抽象類接口多態內部類 1. static static翻譯過來就是靜態的意思static表示靜態&am…
閱讀更多...
AI語音模型PaddleSpeech踩坑（安裝）指南

AI語音模型PaddleSpeech踩坑（安裝）指南

PaddleSpeech簡介 PaddleSpeech 是基于飛槳 PaddlePaddle 的語音方向的開源模型庫&#xff0c;用于語音和音頻中的各種關鍵任務的開發&#xff0c;包含大量基于深度學習前沿和有影響力的模型。 PaddleSpeech安裝步驟 提示&#xff1a;要找到一個合適的PaddleSpeech版本與pad…
閱讀更多...
STM32開發學習——使用 Cortex-M3M4M7 故障異常原因與定位

STM32開發學習——使用 Cortex-M3M4M7 故障異常原因與定位

STM32開發學習——使用 Cortex-M3/M4/M7 故障異常原因與定位 文章目錄 STM32開發學習——使用 Cortex-M3/M4/M7 故障異常原因與定位文檔說明&#xff1a;官方參考文檔線上鏈接&#xff08;可在線閱讀與下載&#xff09;&#xff1a;故障異常處理程序HardFault優先級升級說明故障…
閱讀更多...
java項目之相親網站的設計與實現源碼（springboot+mysql+vue）

java項目之相親網站的設計與實現源碼（springboot+mysql+vue）

風定落花生&#xff0c;歌聲逐流水&#xff0c;大家好我是風歌&#xff0c;混跡在java圈的辛苦碼農。今天要和大家聊的是一款基于springboot的相親網站的設計與實現。項目源碼以及部署相關請聯系風歌&#xff0c;文末附上聯系信息 。 項目簡介&#xff1a; 相親網站的設計與實…
閱讀更多...
連升三級！openGauss單機版從2.1.0經停3.0.0升級至5.0.0

連升三級！openGauss單機版從2.1.0經停3.0.0升級至5.0.0

前言 如前文所述&#xff0c;我們的小demo項目起初安裝了openGauss的2.1.0版本&#xff0c;由于2.1.0不是長期維護&#xff08;LTS&#xff09;版本&#xff0c;所以要升級到5.0.0LTS。考慮到雖然是DEMO項目&#xff0c;但也有些體驗用戶&#xff0c;所以為了保障業務連續性&a…
閱讀更多...
2023版brupsuite專業破解安裝

2023版brupsuite專業破解安裝

安裝教程&#xff0c;分兩部分&#xff1a; 1、安裝java環境、參考鏈接JAVA安裝配置----最詳細的教程&#xff08;測試木頭人&#xff09;_java安裝教程詳細-CSDN博客 2、安裝2023.4版本brupsuite&#xff1a;參考鏈接 2023最新版—Brup_Suite安裝配置----最詳細的教程&…
閱讀更多...
最新文章

Copyright @ 2022~2023