排序在生活中應用很多，對數據排序有按成績，商品價格，評論數量等標準來排序。

數據結構中有八大排序，插入、選擇、快速、歸并四類排序。

目錄

插入排序

直接插入排序

希爾排序?

?選擇排序

?堆排序

冒泡排序?

快速排序?

hoare版本快排

挖坑法

前后指針法?

歸并排序?

---

插入排序

什么是插入排序呢？插入排序就是把一個待排的值插入到已經有序的序列中，直到所有待排的值全部插入到序列中，得到一個新的有序序列。

插入排序有直接插入和希爾排序

直接插入排序

當插入到 i 個數據時，前i個數據已經有序，排第i個數據需要與前 i 個數據依次比較，將第 i 個數據放到合適的位置，根據下面的動圖可以幫助更好的理解

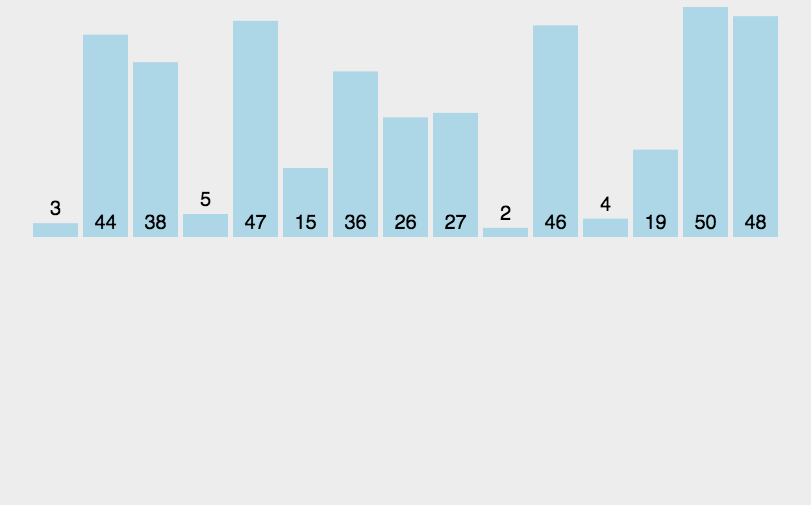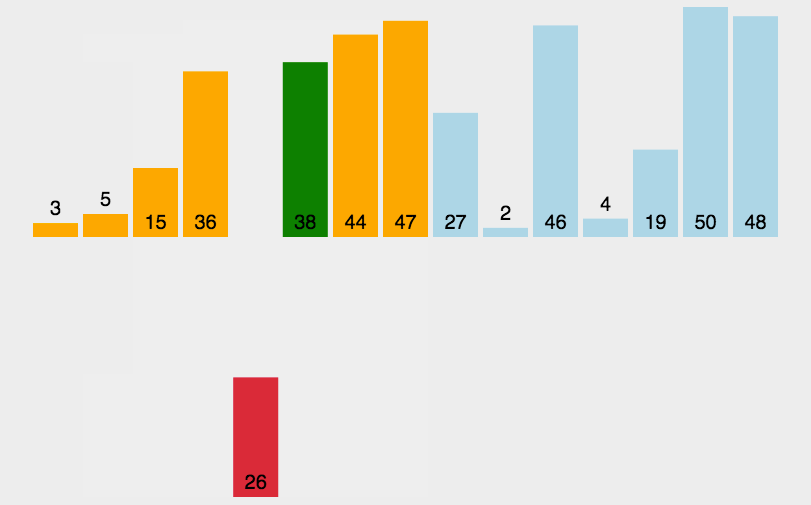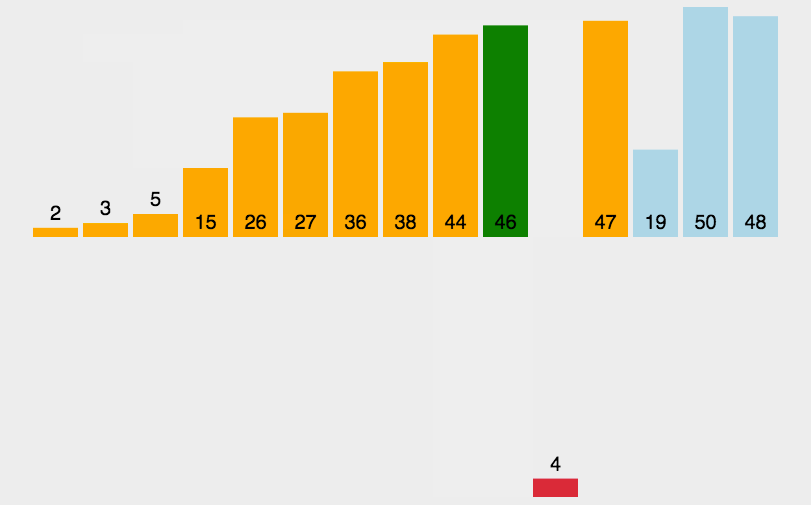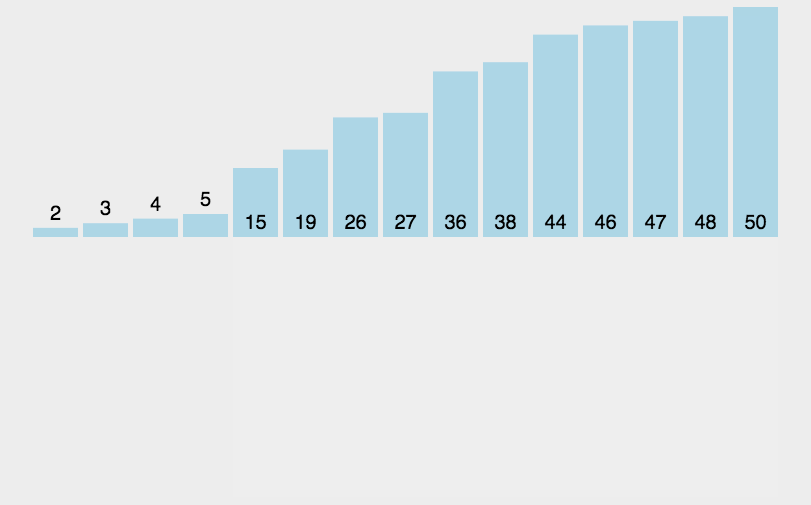
?代碼實現：

void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){int end = i-1;int tmp = a[i];while (end >= 0){if (tmp < a[end]){a[end+1] = a[end];end -= 1;}else{break;}}a[end+1] = tmp;}
}

tmp來存儲需要排序的值，end為需要排序值的前一個位置，tmp從后往前依次比較，當tmp小于end位置的值，就將這個值往后挪動，end往前移動一步?，直到tmp大于或者end不滿足進入循環的條件就把end+1下標的值改為tmp，就把前i個數據排好序了。

時間復雜度：最好情況：O(N) （數據全部有序）

? ? ? ? ? ? ? ? ? ? ? 平均情況：O(N^2)

? ? ? ? ? ? ? ? ? ? ?最壞情況：O(N^2)（數據與我們要排的順序逆序）

空間復雜度：O(1)

穩定性：穩定（判斷穩定性的方法，在這組數據中有兩個相同的數據，在把這組數據排好序后，在未排好時在后的數據不會在排好序后跑到未排好時在前的數據的前面）

在插入排序中如果有兩個數據相同，在排序過程中，相同不會挪動該數據。

希爾排序?

相比與直接插入排序希爾排序多了一個預排序，因為在直接插入排序中，這組數據越有序效率就越快，所以在希爾排序中就先對這組數據預排序，再使用直接插入排序。

那么怎么樣進行預排序呢？如下

?上圖是gap=3的單趟排序。

距離為gap的為一組，按以上數據就可以分為三組，就這三組排序就可以達到預排序的效果，gap越大就分的組就越多，當gap=1時就是直接插入排序，所以我們可以先讓gap為一個比較大的值，為數據個數的二分之一，一直減小直到為1，就排好序了。

代碼展示：

void ShellSort(int* a, int n)
{int gap = n;while (gap>1){gap = gap / 2;//gap == 1 就是插入排序//gap > 1 預排序for (int j = 0; j < gap; j++){for (int i = gap + j; i < n; i += gap){int end = i - gap;int tmp = a[i];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}

?為什么這樣效率會更快呢？，gap = 2^2^2^2^2……2^2,循環次數為logN，內循環為N，所以希爾排序的時間復雜度為NlogN（底為2）。

時間復雜度：最好情況：O(N^1.3)

? ? ? ? ? ? ? ? ? ? ?平均情況：O(NlogN~N^2)

? ? ? ? ? ? ? ? ? ? ? 最壞情況：O(N^2)

空間復雜度：O(1)

穩定性：不穩定（因為在預排序時可能會把兩個相同的數的相對前后位置改變）

?選擇排序

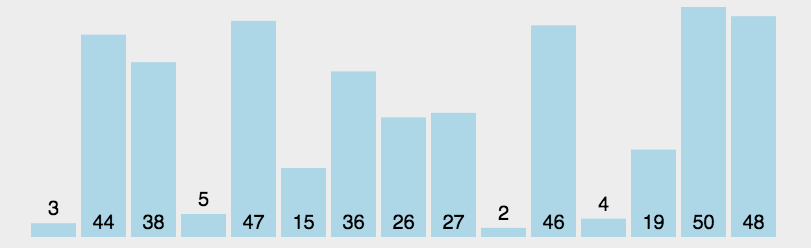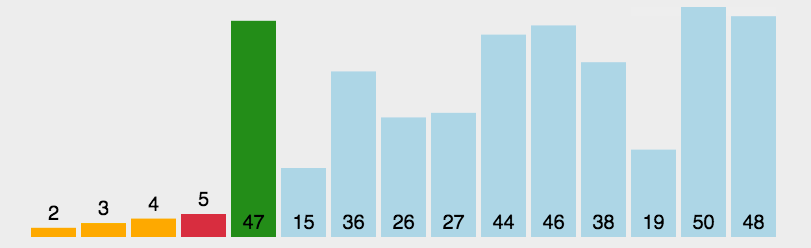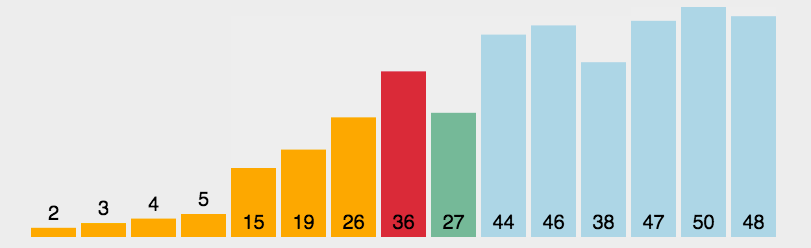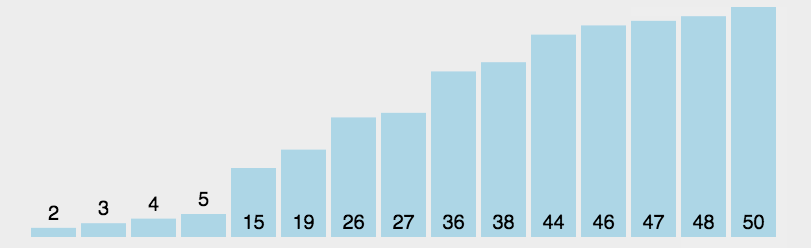
選擇排序思想：每次選擇待排序數據中最小（最大）的數據，存放在待排序列起始位置，直到全部數據排完。

?代碼實現：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void SelectSort(int* a, int n)
{int left = 0, right = n - 1;while (left < right){int maxi = left, mini = left;for (int i = left + 1; i <= right; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[left], &a[mini]);if (left == maxi || right == mini){maxi = mini;}Swap(&a[right], &a[maxi]);left++;right--;}
}

這里我們思想是和選擇一樣的，只不過我們使用雙指針從待排序列的兩邊開始，在序列中找最大和最小值，最小值放到待排的序列起始位置，最大的值放到待排序列的最后一個位置，當兩個指針相等時就結束循環，這里需要注意的是在最小值交換到待排序列的位置時，left為待排序列的起始位置，right為最后一個位置，當left等于最大值的下標或者right等于最小值的下標時，需要將最小值的下標給最大值的下標。例如排序3、2、1、0。

這里進行了第一次交換，如果沒有判斷的話直接進入第二次交換就回到第一次交換之前， 這兩個數據就沒有發生變換，導致排序失敗。

時間復雜度：最好情況：O(N^2)

? ? ? ? ? ? ? ? ? ? ? 平均情況：O(N^2)

? ? ? ? ? ? ? ? ? ? ? 最壞情況：O(N^2)

空間復雜度：O(1)

穩定性：不穩定

示例：

?堆排序

堆排序是利用堆積樹來這種數據結構所設計的一種算法，通過堆來選數據，排升序要建大堆（每一個子樹都滿足雙親大于兩個孩子），排降序建小堆（每一個子樹都滿足雙親小于兩個孩子）。

在我之前的文章有堆更詳細的講解，更好幫住理解堆排序：https://blog.csdn.net/lrhhappy/article/details/147029631?spm=1001.2014.3001.5502

代碼展示：

void AdjustDwon(int* a, int n, int parent)
{int child = parent * 2 + 1;while ((parent*2+1) < n){if ((child + 1) < n && a[child] < a[child + 1]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{//建堆for (int i = (n-2)/2; i>=0; i--){AdjustDwon(a, n, i);}printArr(a, n);int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);end--;}printArr(a, n);
}

時間復雜度 ：最好情況：O(NlongN)

? ? ? ? ? ? ? ? ? ? ? ?平均情況：O(NlongN)

? ? ? ? ? ? ? ? ? ? ? ?最壞情況：O(NlongN)

空間復雜度：O(1)

穩定性：不穩定? （想想示例）

冒泡排序?

冒泡排序在是在初學是最早接觸的排序，但是實際應用不怎么用，相比其他排序效率太低了。

冒泡思想：將鍵值較大的記錄向序列的尾部移動，鍵值較小的記錄向序列的前部移動。每次從序列起始位置開始與下一個位置比較，如果該位置大于下一個位置的值，就進行交換，就把最大的值換到序列的最后一個，循環往復，就可以排完全部數據。?

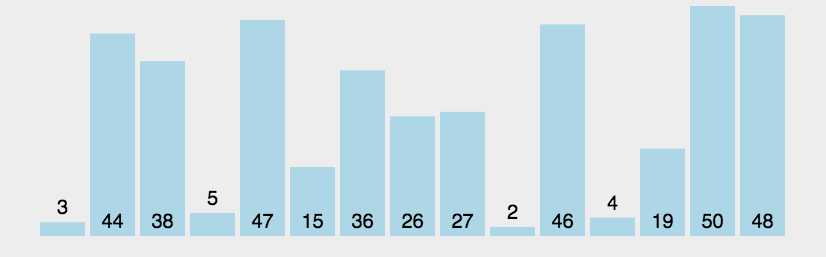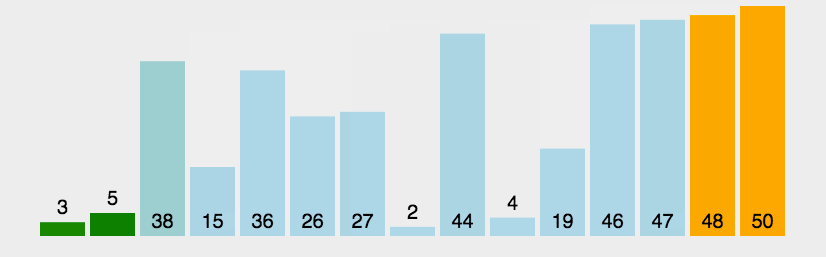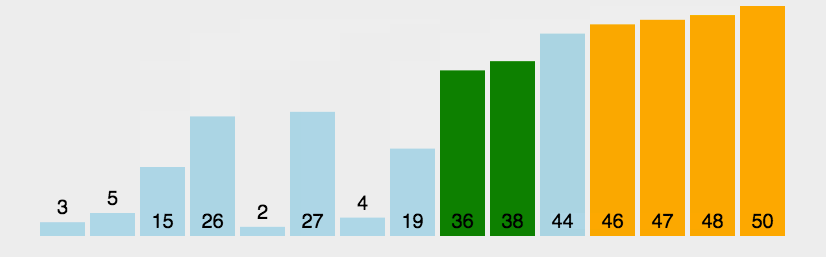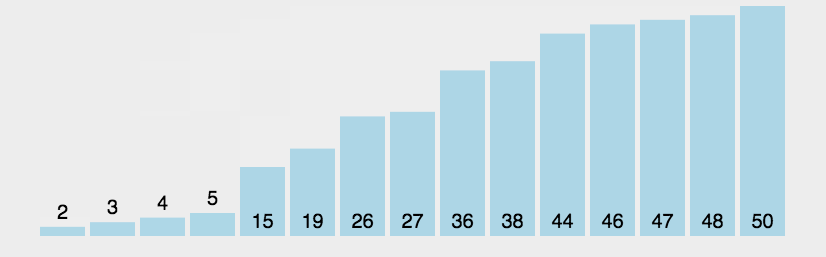
代碼展示：

//冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j <n-i-1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}

時間復雜度：O(n^2) （不管要排序的序列是否有序，都需要進行比較）

空間復雜度：O(1)

穩定性：穩定（相等不會交換）?

快速排序?

hoare版本快排

hoare快排思想：任取待排序元素序列中的某元素作為基準值，按照該排序碼將待排序集合分割成兩子序列，左子序列中所有元素均小于基準值，右子序列中所有元素均大于基準值，然后最左右子序列重復該過程，直到所有元素都排列在相應位置上為止。

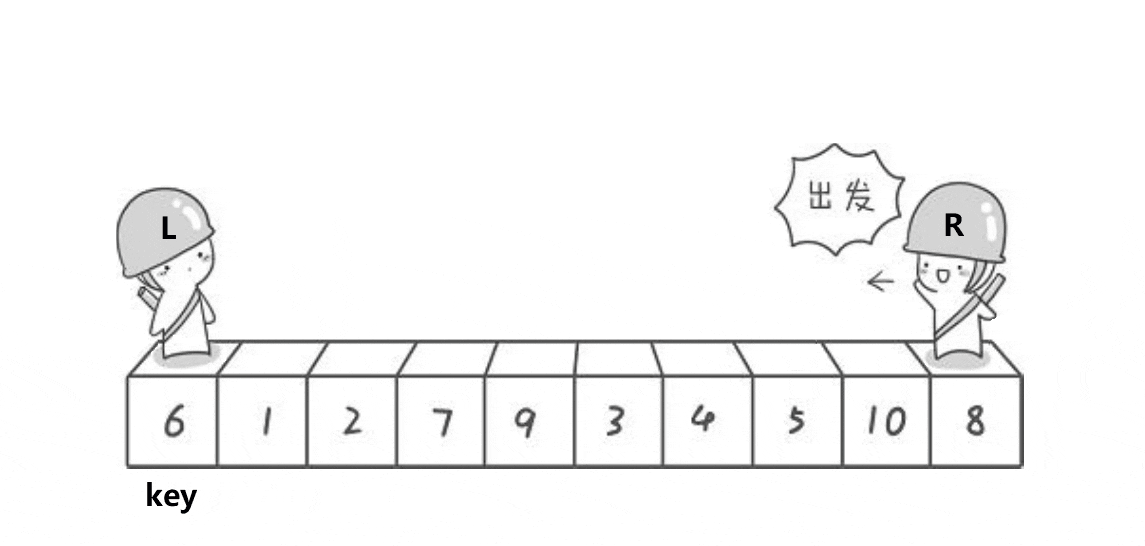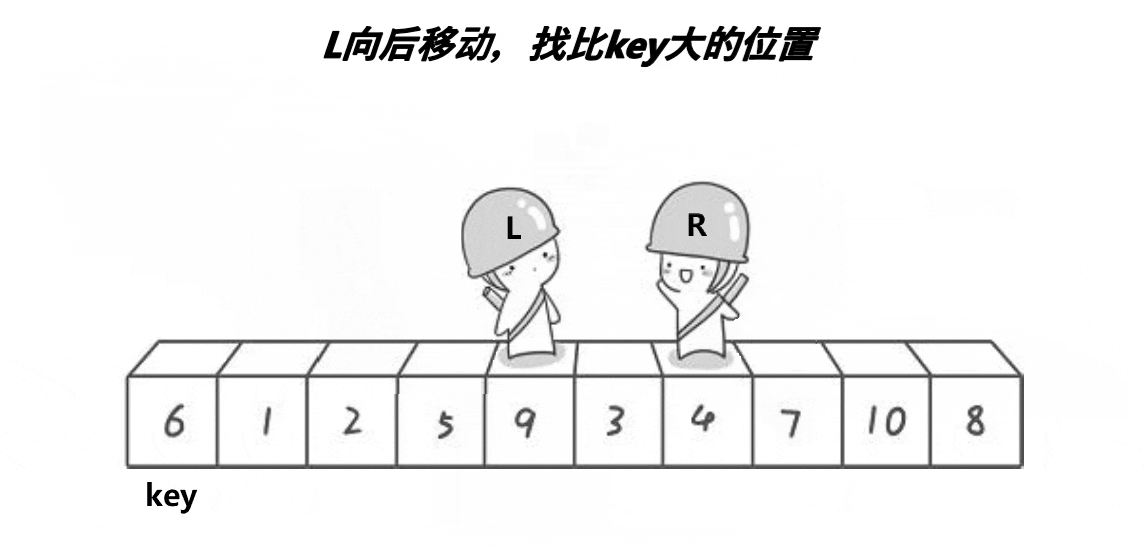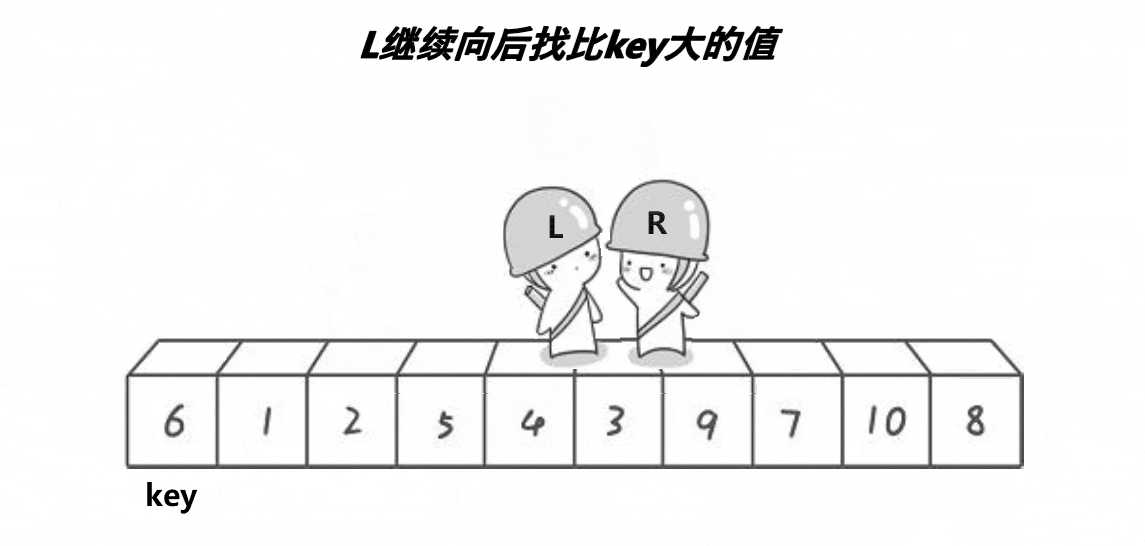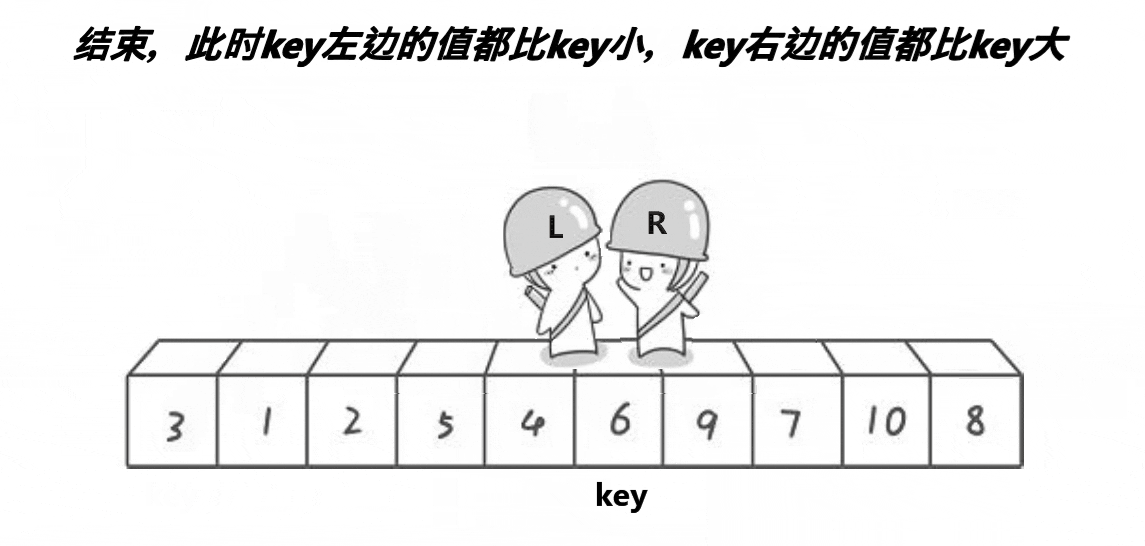
代碼展示：

//三數取中
int GetMidi(int* a,int left, int right)
{int mid = (right - left) / 2;if (a[left] > a[mid]){if (a[right] > a[left]){return left;}else if (a[mid] > a[right]){return mid;}else{return right;}}else // a[left] < a[mid]{if(a[right]>a[mid]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}
}
//快排
void PartSort1(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//隨機數法/*int reti = left + (rand() % (right - left));Swap(&a[left], &a[reti]);*///三數取中法int reti = GetMidi(a,left,right);Swap(&a[left], &a[reti]);int keyi = left;while (left < right){//找小while (left < right && a[right] >= a[keyi])right--;//找大while (left < right && a[left] <= a[keyi])left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;PartSort1(a, begin, keyi - 1);PartSort1(a, keyi + 1, end);
}

根據上面的圖可以得出大概的邏輯，left為序列的起始位置下標，right為最后一個數據的下標，選起始位置下標為keyi，right目標是找小于或者等于keyi位置的值，left的目標是找大于或者等于keyi位置的值，right先走，left再走，兩個對應的值進行交換，當left等于right時與keyi位置的值交換，就完成了單趟的排序，以keyi位置分為兩個區間[left,keyi] keyi [keyi+1,right],接著排這兩個區間，排完就排四個區間……，從這里就可以知道使用遞歸會更好

注意：left和right在走的時候需要滿足left小于right。

?這里用到三數取中，以及隨機取數，這里更推薦三數取中，這兩個是對快排的優化，使keyi選擇這個序列中更中間的數，更可以提高該算法的效率。

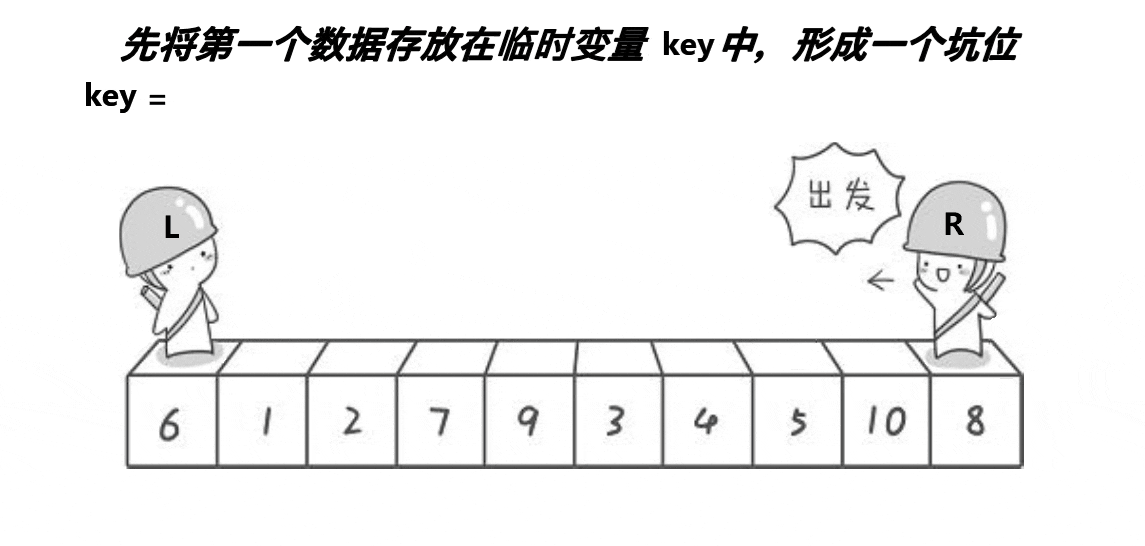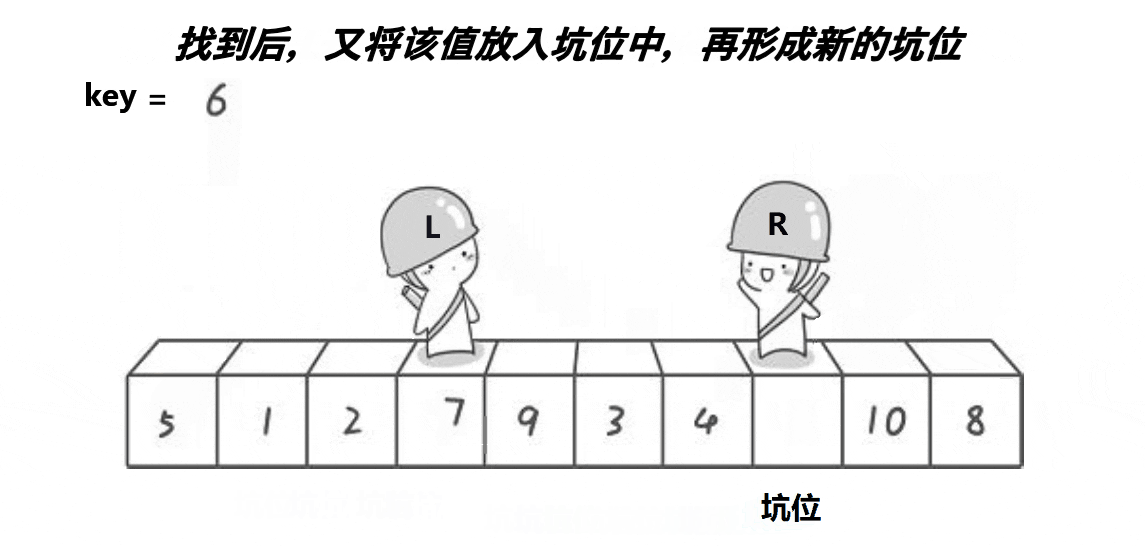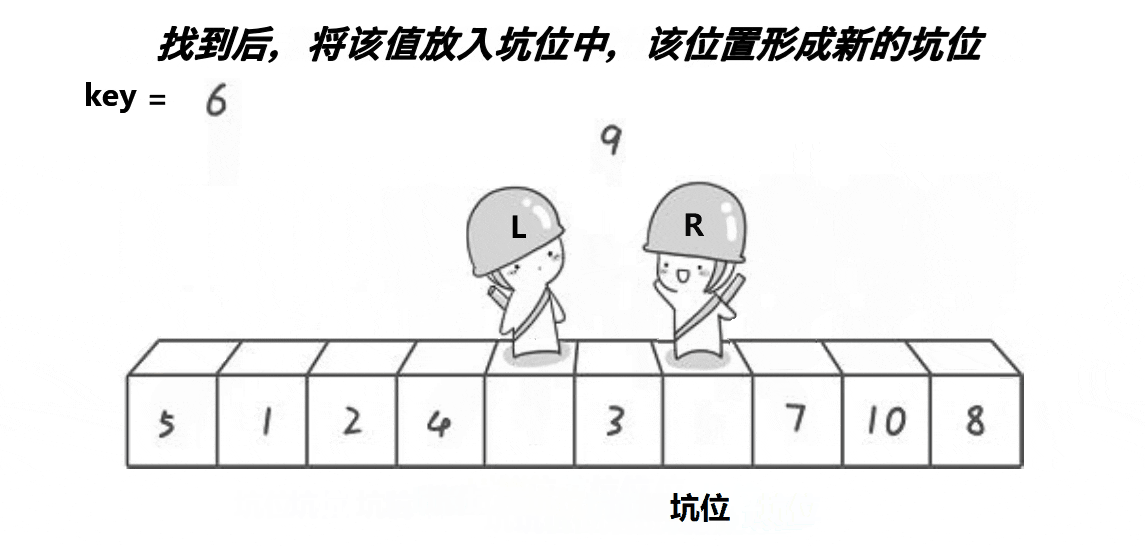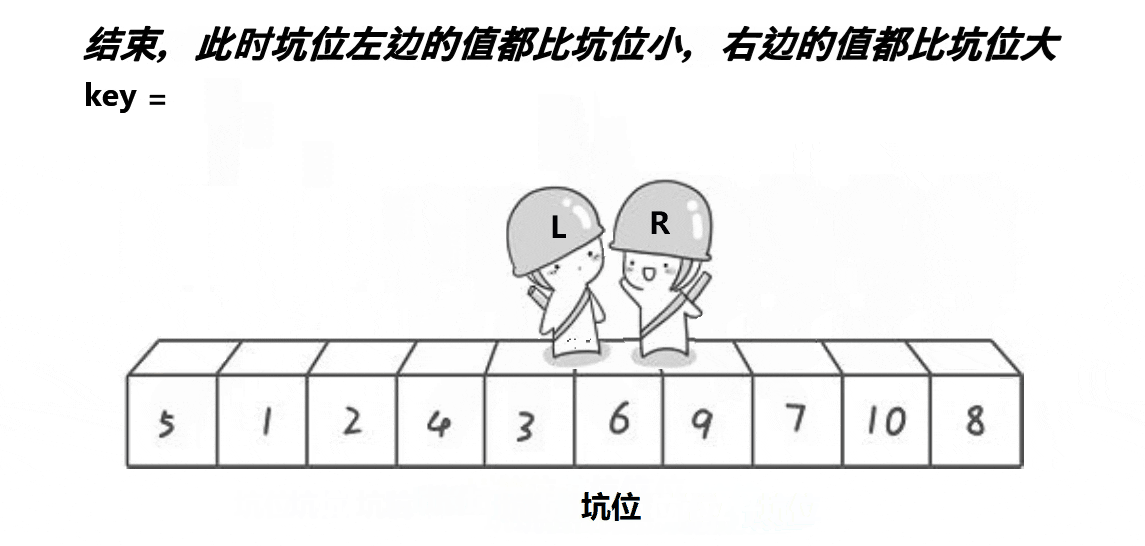
挖坑法

挖坑法key保存的是起始位置（看圖中保存的是起始位置的值，因為創建的key是局部變量），當左邊為key值，就需要先讓右邊先走，反之左邊先走，定義一個變量key來存放起始位置，right先走，目標是找比key對應值小的值，再把right對應值給left對應值，接著left走，目標是找比key對應值大的值，找到之后把left對應值給right對應值，直到left和right相等，相等位置的值被賦值key對應值，這只是單趟的排序，這里使用遞歸，與hoare一樣分兩個、四個……區間，直到left大于或者等于right就返回。

void PartSort2(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//隨機數法/*int reti = left + (rand() % (right - left));Swap(&a[left], &a[reti]);*///三數取中法/*int reti = GetMidi(a, left, right);Swap(&a[left], &a[reti]);*/int key = a[left];while (left < right){//找小while (left < right && a[right] >= key)right--;a[left] = a[right];//找大while (left < right && a[left] <= key)left++;a[right] = a[left];}a[left] = key;PartSort1(a, begin, left - 1);PartSort1(a, left + 1, end);
}

當完成一趟排序后，key對應值就到了最終排完后的位置，所以只需要對key對應值前后區間排序就可以，創建兩個變量begin和end來存儲當前序列的起始位置和末尾，遞歸時用得上。

前后指針法?

思想：創建兩個變量prev和cur，prev在起始位置，cur在prev后一個位置，先對cur對應值和key對應值比較，如果小于key對應值就prev++，然后再交換prev和cur的值，cur++，如果大于key對應值，只cur++。

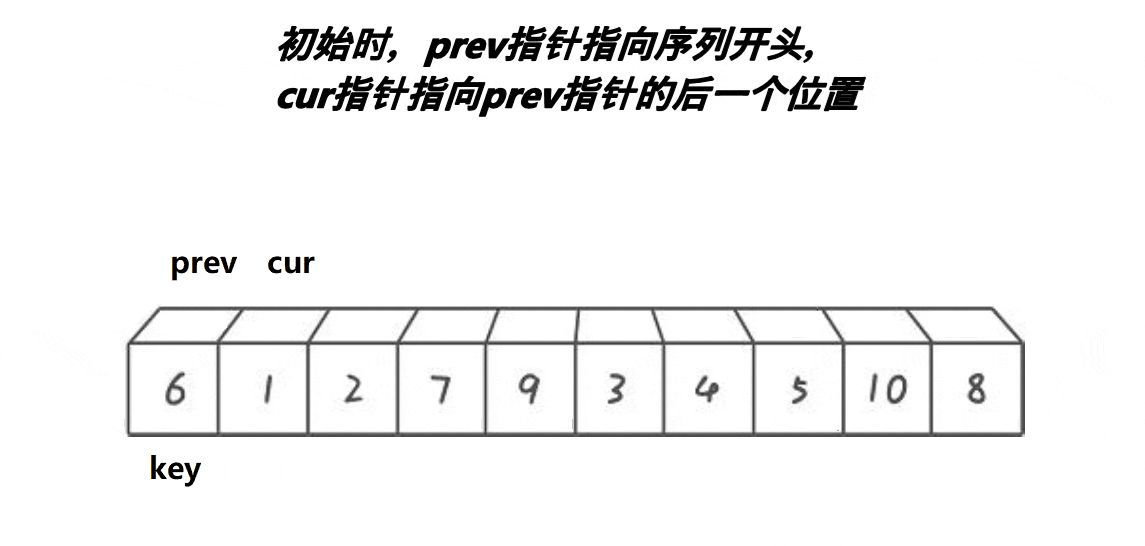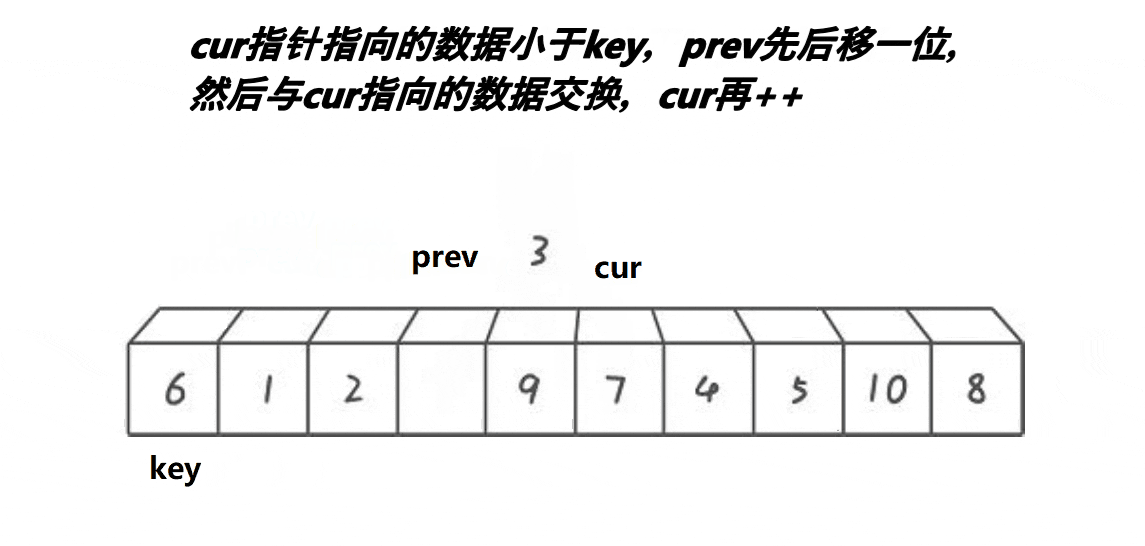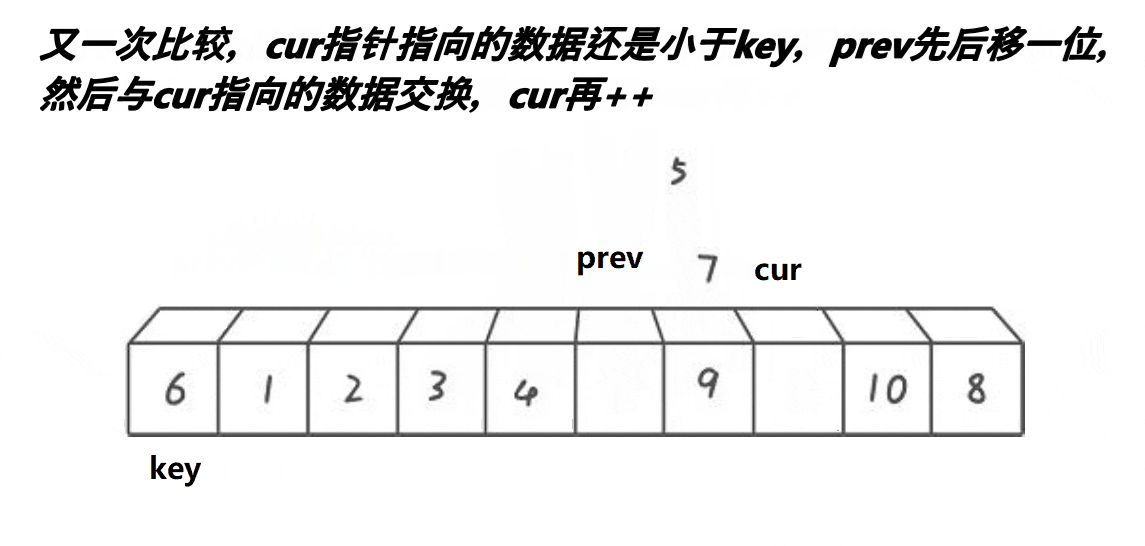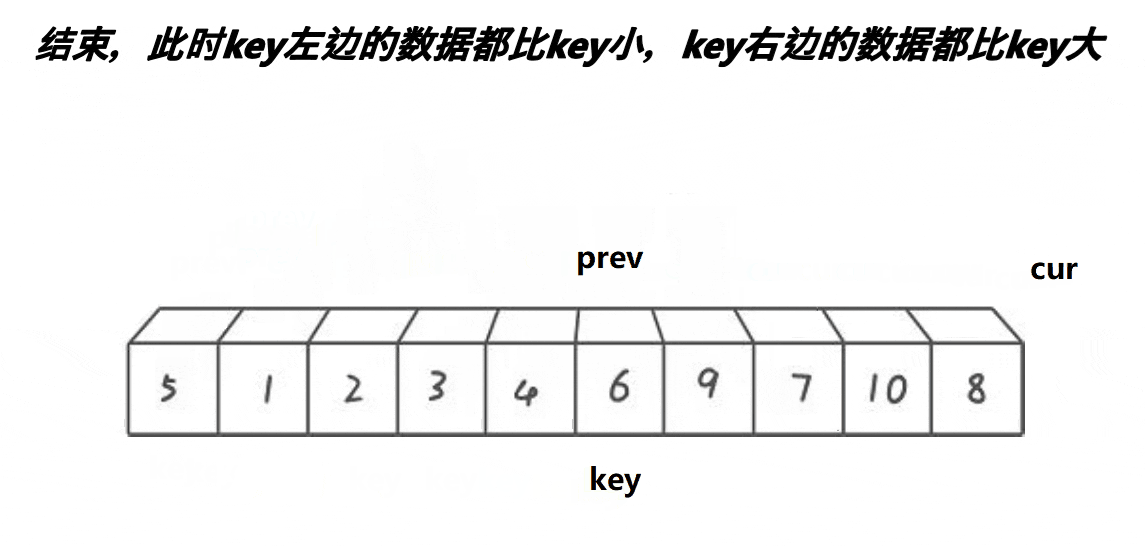
void PartSort3(int* a, int left, int right)
{if (left >= right)return;int prev = left, cur = left + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi]){prev++;Swap(&a[cur],&a[prev]);}cur++;}Swap(&a[keyi], &a[prev]);//優化前/*PartSort3(a, left, prev - 1);PartSort3(a, prev + 1, right);*///優化后if ((right - left + 1) > 10)//在數據量大的時候可以省去很多次遞歸，分割成很多小區間時使用插入排序。{PartSort3(a, left, prev - 1);PartSort3(a, prev + 1, right);}else{//插入排序InsertSort(a + left, right - left + 1);}
}

?創建兩個變量prev和cur，prev在起始位置，cur在prev后一個位置，根據上面的思想寫出代碼，cur需要小于或者等于right，完成單趟就遞歸，這里進行了優化，因為遞歸就像二叉樹的結構，在最后一層遞歸數量占一半了，我們可以在遞歸只剩最后幾層時使用直接插入排序就可以增加算法效率，當區間小于十就開始使用插入排序。

時間復雜度：最好情況：O(NlogN)

? ? ? ? ? ? ? ? ? ? ?平均情況：O(NlogN)

? ? ? ? ? ? ? ? ? ? ?最壞情況：O(N^2)

空間復雜度：O(logN~N)

穩定性：不穩定

示例：

歸并排序?

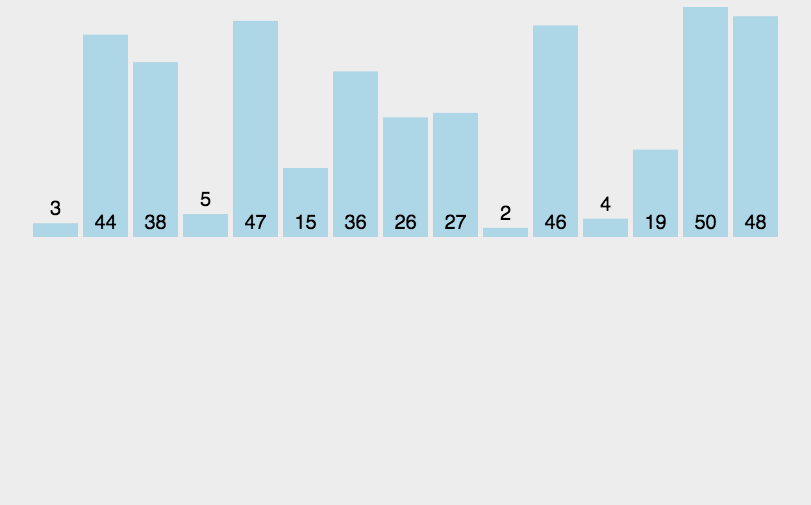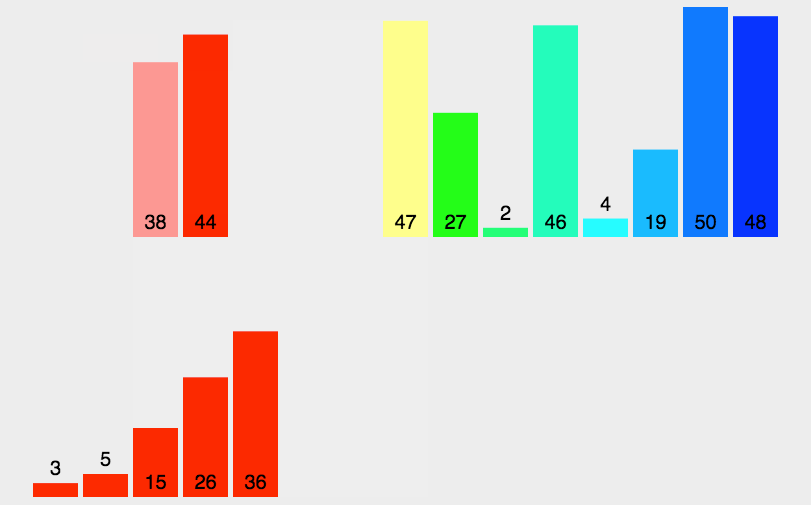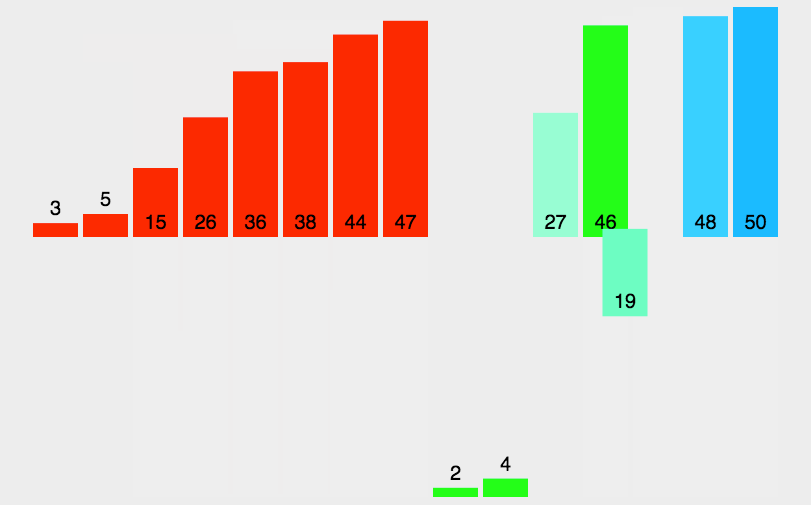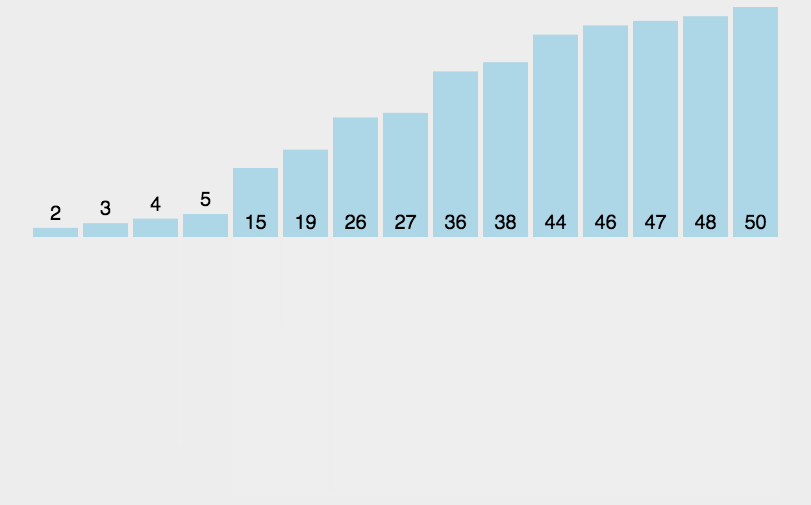
基本思想：歸并排序是建立在歸并操作上的一種有效的排序算法,該算法是采用分治法的一個非常典型的應用。將已有序的子序列合并，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合并成一個有序表，稱為二路歸并。

?

從上面的圖可以更好的理解歸并排序，將序列逐漸分為一個，再兩個兩個對比，這時就需要一個新的數組來存放排序后的數據，小的數據先放進新的數組，則每個序列對比時都是有序的，在把兩個有序的序列合并成一個新的有序序列，直到將全部的小序列合并成一個有序序列就完成了歸并排序?。

代碼展示：

//歸并排序子函數
void _Mergesort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (right + left) / 2;_Mergesort(a, left, mid, tmp);_Mergesort(a, mid + 1, right, tmp);int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int j = left;//歸并while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}//歸并排序函數
void Mergesort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_Mergesort(a,0,n-1,tmp);free(tmp);
}

歸并排序需要分為兩個函數，因為這里是寫遞歸的歸并，開辟數組只需要開辟一次，所以我們在另一個函數寫歸并排序，歸并排序就相當于后序遍歷，先將序列分為一個一個再進行比較。

時間復雜度：O(NlogN)

空間復雜度：O(N)

穩定性：穩定