


目錄
一、快速排序(非遞歸)
1.原理
2.實現
2.1 stack
2.2 partition(array,left,right)
2.3 pivot - 1 > left
二、歸并排序(非遞歸)
1.原理
2.實現
2.1 gap
2.1.1 i += 2*gap
2.1.2 gap *= 2
2.1.3 gap < array.length
2.2 left、mid、right
2.2.1 left = i
2.2.2 mid >= array.length
前言:
?在看快速排序的非遞歸實現之前,可以先看看快速排序用遞歸實現的版本:【算法】快速排序(遞歸實現),里面有詳細介紹下面講到的基準排序,基準排序是快速排序實現的基礎,最好先去了解下再往下看
遞歸實現歸并排序的也獻上:【算法】歸并排序(遞歸實現)
一、快速排序(非遞歸)
1.原理
- 在每一個待排元素所確定在的待排序區間內把待排序元素用基準排序一個個排好,等到把所有待排序區間對應的一個個待排序元素都排好后,整個數組就排好了
(在區間內進行基準排序時,默認以區間第一個元素為待排序元素)
用基準排序把每一個元素在對應已知的待排序范圍排好,因為每排好一個元素,此元素排序位置確定且其排出的左小右大性質能縮小剩余的元素的待排序范圍區域,所以每當一個元素排好后,其余元素對應的已知待排序范圍就會發生變化,所以元素所在的待排序區域是經過動態變化來的
2.實現
public static void quickSortNonR(int[] array) {Stack<Integer> stack = new Stack<>();//2.1int left = 0;int right = array.length-1;int piovt = partition(array,left,right);//2.2if(piovt - 1 > left) {//2.3stack.push(left);stack.push(piovt-1);}if(piovt + 1 < right) {stack.push(piovt+1);stack.push(right);}while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();piovt = partition(array,left,right);if(piovt - 1 > left) {stack.push(left);stack.push(piovt-1);}if(piovt + 1 < right) {stack.push(piovt+1);stack.push(right);}}}//2.2基準排序挖坑法實現:private static int partition(int[] array,int left,int right) {int key = array[left];while (left < right) {while (left < right && array[right] >= key) {right--;}//right下標元素一定比key小array[left] = array[right];while (left < right && array[left] <= key) {left++;}//left下標元素一定比key大array[right] = array[left];}array[left] = key;return left;}2.1 stack
利用棧的動態進出存儲刪取管理這些動態區間
2.2 partition(array,left,right)
partition方法是默認拿待排序區間的第一個元素為基準完成該元素在待排序區間內排好的
2.3 pivot - 1 > left
說明剩下的左邊的待排序區域至少有兩個元素,還是需要去進行基準排序的
二、歸并排序(非遞歸)
1.原理
一輪輪去有序數組gap的兩兩合并,去合并的有序數組單位會越來越大,直到最后一次兩兩合并后成的是整體數組的一個有序數組,數組就整體排好序了
2.實現
public static void mergeSortNor(int[] array) {int gap = 1;//2.1while (gap < array.length) {//2.1.3for (int i = 0; i < array.length; i += 2*gap) {//2.1.1int left = i;//2.2.1int mid =left+gap-1;int right = mid+gap;if(mid >= array.length) {//2.2.2mid = array.length-1;}if(right >= array.length) {right = array.length-1;}merge(array,left,right,mid);}gap *= 2;//2.1.2}}private static void merge(int[] array, int left, int right, int mid) {int s1 = left;int s2 = mid+1;int[] tmpArr = new int[right-left+1];int k = 0;//證明兩個區間都同時有數據的while (s1 <= mid && s2 <= right) {if(array[s2] <= array[s1]) {tmpArr[k++] = array[s2++];}else {tmpArr[k++] = array[s1++];}}while (s1 <= mid) {tmpArr[k++] = array[s1++];}while (s2 <= right) {tmpArr[k++] = array[s2++];}//tmpArr里面一定是這個區間內有序的數據了for (int i = 0; i < tmpArr.length; i++) {array[i+left] = tmpArr[i];}}2.1 gap
每輪去兩兩合并的單有序數組的元素個數,最開始的單位有序數組長度是1
2.1.1 i += 2*gap
一輪中往后繼續去合并下一對的兩gap有序數組
2.1.2 gap *= 2
一輪全部兩兩合并完后gap單位有序數組長度已翻倍
2.1.3 gap < array.length
gap >= array.length時,繼續去有序數組合并也都只有一個靠前的左數組(整體數組),去合并也是沒有變化了,且其實在gap >= array.length之前就一定有最后一次的兩兩合并成整體有序數組的了
2.2 left、mid、right
- [left,mid] —> 兩合并數組中靠前的gap長度有序數組
- (mid,right] —>?兩合并數組中靠后的gap長度有序數組
2.2.1 left = i
i < array.length,再進來的left是一定是left < array.length的
2.2.2 mid >= array.length
- 如果mid <?array.length 但 right >=?array.length:
左右兩數組靠前的正常滿足gap長度,靠后的不足gap長度,merge合并時也是正常合并
- 如果mid >=?array.length - 1:
只有一個靠前的左數組,merge合并后還是它沒變的左數組
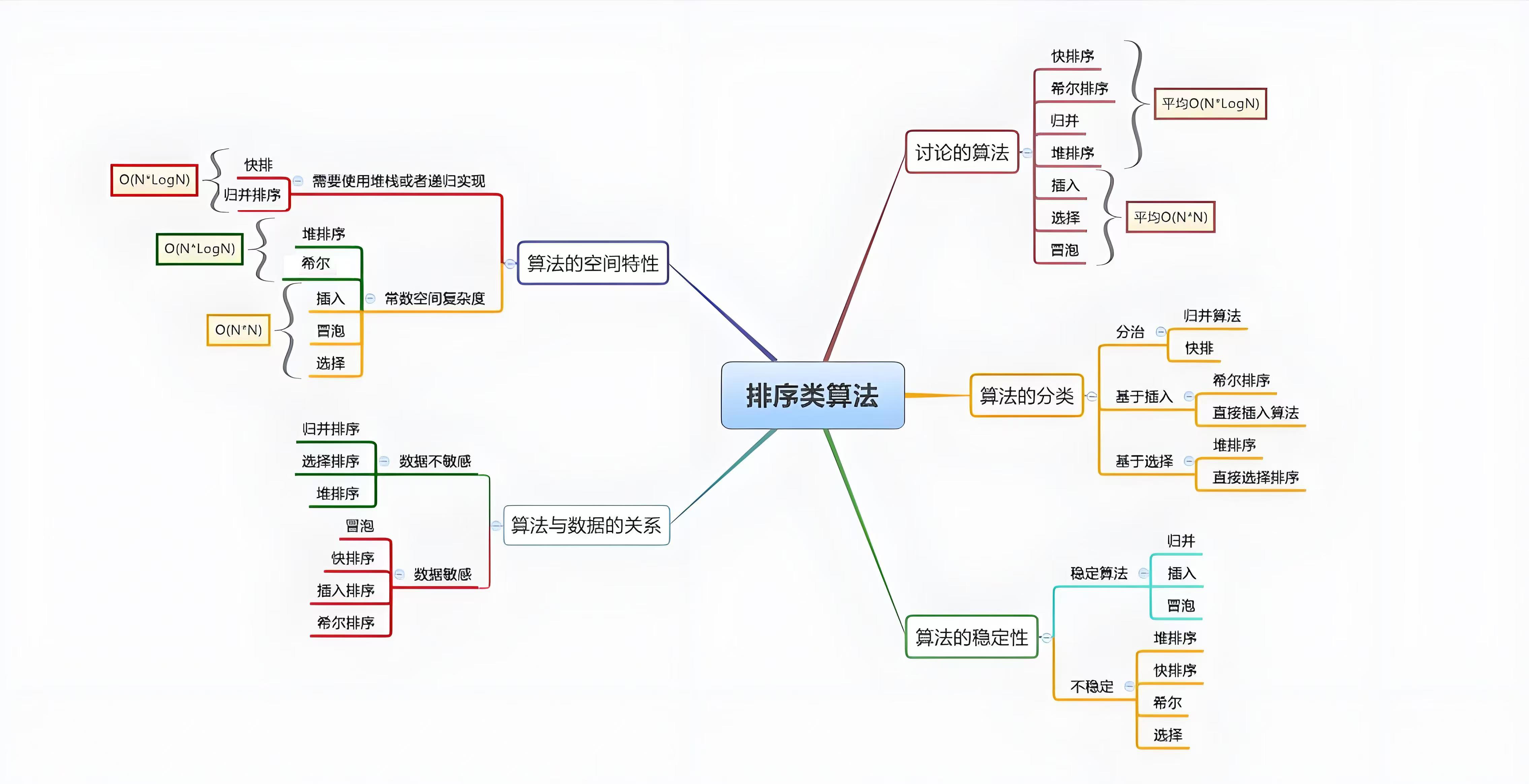
三、排序總結





 (傳輸協議層:UDP、TCP))






——ViT理解與應用)







)