目錄
一、基于采樣的規劃方法概述
二、概率路圖（PRM）
1、核心思想?
2、實現流程
3、算法描述
4、節點連接處理
5、總結
三、快速搜索隨機樹（RRT）
1、核心思想
2、實現流程
?3、總結
4、改進RRT算法
①快速搜索隨機圖（RRG）
②基于運動學的快速搜索隨機樹（Kinematic-based RRT）
一、基于采樣的規劃方法概述
? ? ? ? 基于采樣的方法就是在狀態空間中不斷地隨機撒點，將這些節點根據一定的規則與周圍的節點進行連接，以此構造一條條局部路徑，最終找到一條從起點到終點的路徑。隨著采樣點的不斷增多，最終得到的解會不斷逼近最優解。
? ? ? ? 一般步驟：
- 為圖表添加隨機數種子
- 以某種策略或者給定條件采樣到起始節點
- 選擇和哪些其他節點進行連接
- 選擇添加或者移除哪些邊
二、概率路圖（PRM）
1、核心思想?
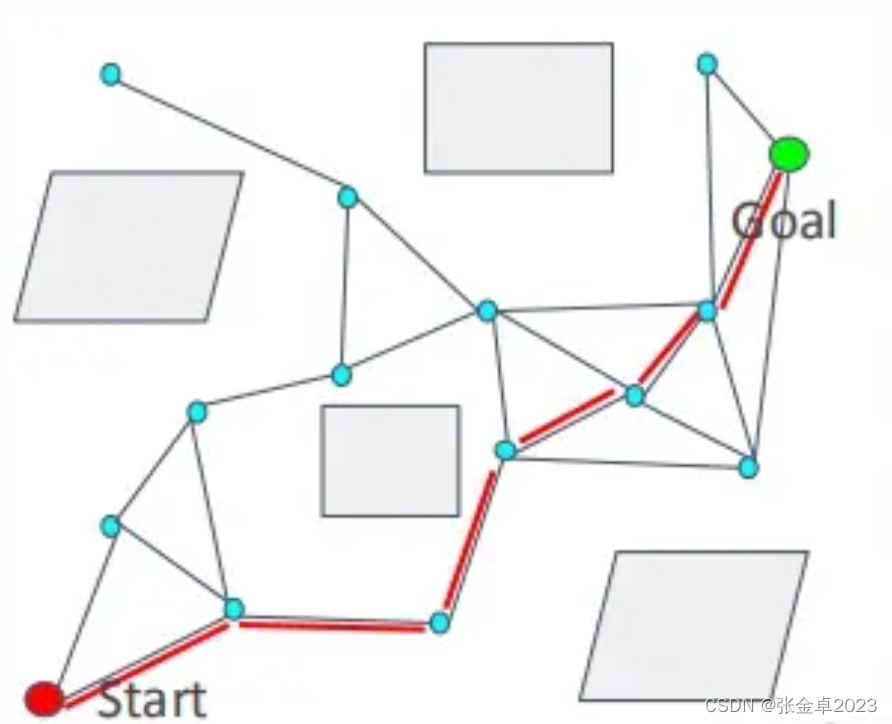
? ? ? ? PRM有兩個階段分別是學習階段（Learning Phase）和查詢階段（Query Phase）。
? ? ? ? 學習階段：
- 在配置空間中隨機采樣足夠數量的點；
- 將相互之間能夠到達的節點進行連接。
? ? ? ? 查詢階段：
- 利用圖搜索算法尋找圖表中從起始節點到目標節點的路徑。?
2、實現流程
（a）圖中所示為一個用于采樣的配置空間，在配置空間中，自動駕駛車輛可以被近似看成一個質點，環境中的障礙物等信息都被近似為圖中的forbidden space，自動駕駛車輛在free space空間中運動，二無需考慮其幾何形狀和運動狀態；
（b）圖中通過隨機采樣的方式獲得一個坐標點，采樣的方法也要根據特定的場景做出不同的選擇，常見的采樣算法有均勻分布采樣（在未知場景中采樣）、高斯分布采樣（在自動駕駛場景中通常以車道中心線為均值）等；
?（c）圖中通過采樣大量的點來獲取地圖的形狀；
?（d）圖中對采樣點進行碰撞檢驗，刪除forbidden space中的采樣點；
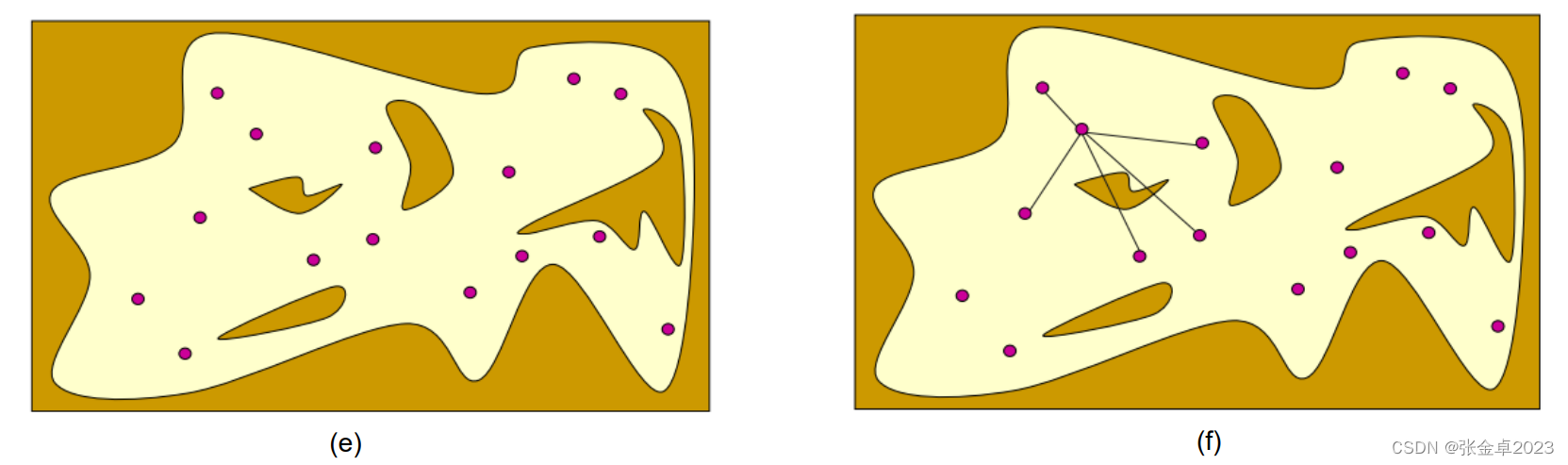
?（e）圖中為刪除forbiden space中的采樣點后，在free space中保留下來的有效采樣點；
? （f）圖中每個有效采樣點會連接以當前節點為圓心，半徑r圓形范圍內的所有采樣點
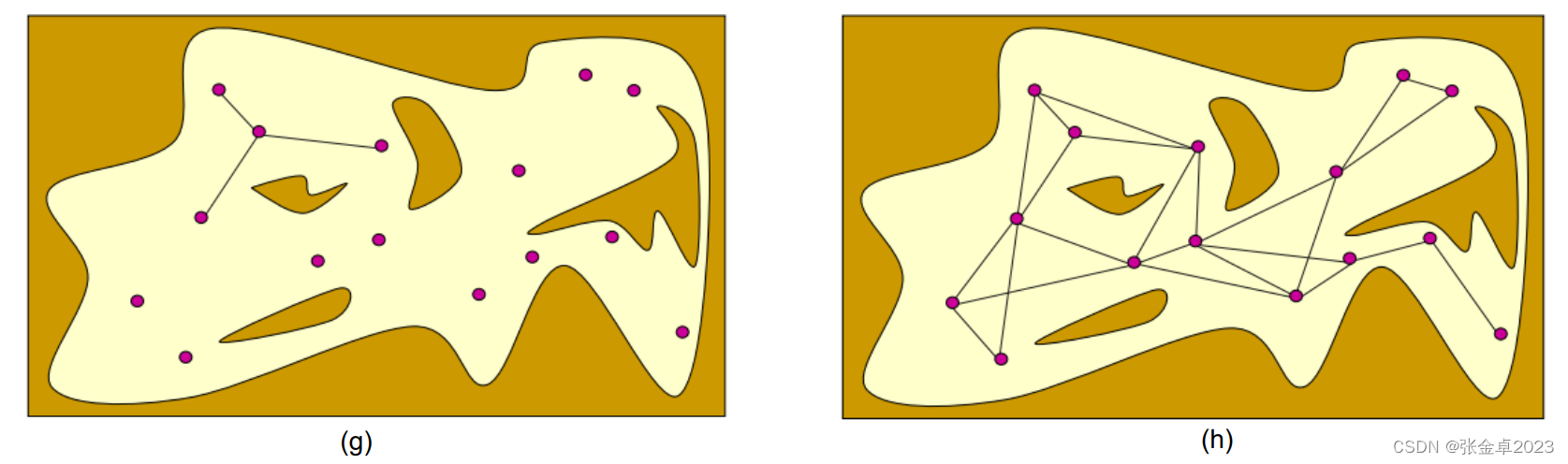?（g）圖中若采樣點之間的連線與forbiden space相交則發生碰撞，刪除發生碰撞的連線；
? （f）圖中碰撞檢測通過的連線得到保留，作為構成圖表graph的邊；
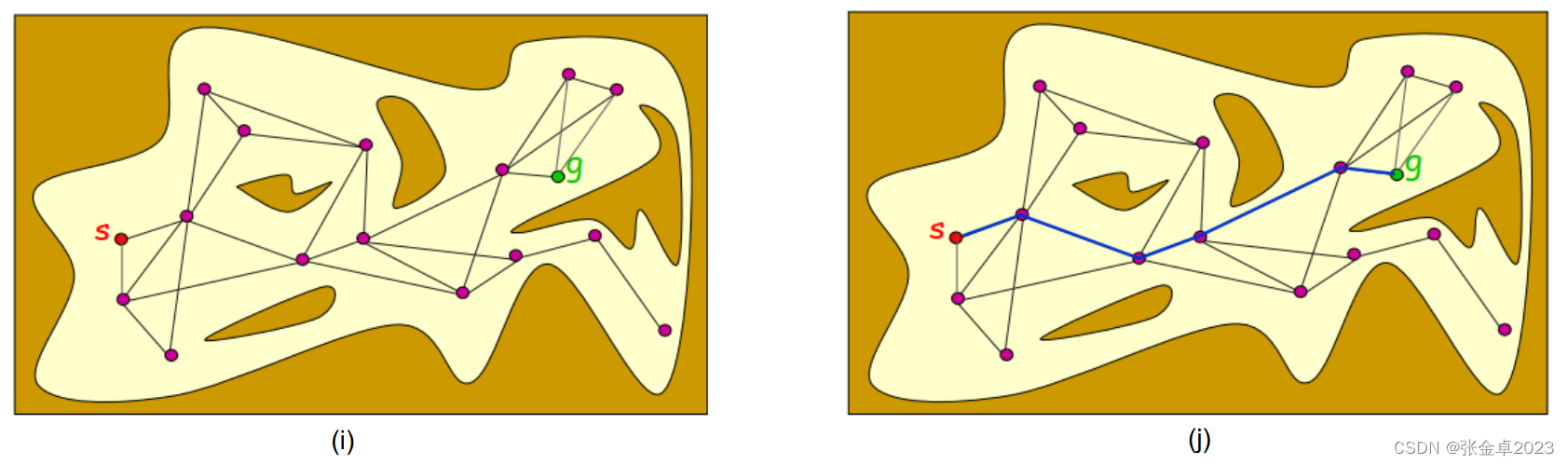
?（i）在連線得到的圖表graph中添加起始節點和目標節點；
?（j）在graph圖中利用圖搜索算法尋找最優路徑。
3、算法描述
? ? ? ? 用偽代碼的方式對PRM進行簡要描述：
V <- ?; E <- ? // 分別維護兩個集合，一個存放頂點，一個存放邊
for i = 0,...,n do //假定最大采樣點為n，進入循環x <- SampleFree; //在freespace通過特定的采樣策略采樣得到一個節點U <- Near(G = (V,E), x, r); //將節點半徑r范圍內要專注的鄰居節點加入集合U中V <- V ∪ {x}; //將當前采樣點x加入集合V中，更新集合Vforeach u in U, in order of increasing ||u - x||, do //對集合U中存入的節點進行處理，為了避免節點過于密集，u和x不能過于接近if x and u are not in the same connected component of G = (V,E) then // 保證u和x之間的連線與其他連線不重合if CollisionFree(x,u) then E <- E∪{(x,u),(u,x)}; // 通過碰撞檢驗則將x和u的連線加入集合E
return G=(V,E); // 返回V和E表示的圖? ? ? ? 上面是經典的PRM算法描述，也可以對其進行簡化：
V <- {x}∪{SampleFree}; E <- ?;
foreach v in V do U <- near(G=(V,E),v,r)\{v};foreach u in U doif CollisionFree(v,u) then E <- E∪{(v,u),(u,v)}
return G=(V,E);? ? ? ? 主要就是減少了剔除部分節點的步驟，因此在算法實現上效率會降低。
4、節點連接處理
? ? ? ? 在PRM實現過程中，選擇那些節點相連也是需要考慮的問題，下面給出三種可行的方法：
- k-Nearest PRM：選擇當前節點最近的k個鄰居節點
U ← kNearest(G=(V,E),v,k)
- Bounded-degree PRM：對半徑范圍內添加的最近節點添加一個邊界值k
U ← Near(G,x,r) ∩?kNearest(G=(V,E),v,k)
- Variable-radius PRM：讓連接半徑稱為對應節點個數的函數，而不是固定的參數
5、總結
? ? ? ? PRM優點：具有概率完備性，只要采樣點足夠多，并且生成的圖表有解那么一定可以結合圖搜索算法找到一條最優解路徑；
? ? ? ? 缺點：
- 如果是連接特定起點和終點，那么通過PRM的兩個階段先建圖在搜索是比較浪費資源的；
- 搜索得到的路徑是節點之間通過直線連接的，不符合車輛的運動學約束。
三、快速搜索隨機樹（RRT）
1、核心思想
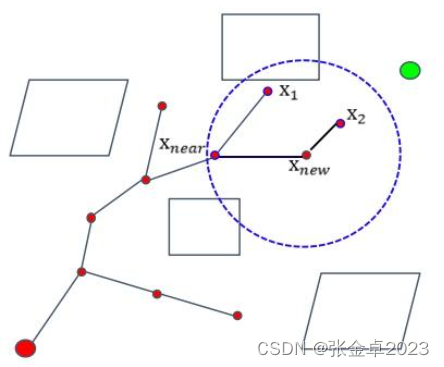
? ? ? ? 與PRM有學習和查詢兩個階段，并且在學習階段構造的是一個圖不同，RRT只有一個階段，在采樣結束的同時就能確定路徑，RRT在采樣的過程中維護的是一個樹結構。相比圖描述的網絡關系，樹結構描述的是一種層次關系。
? ? ? ? 在RRT算法中，通常將起始節點作為樹的根節點，在采樣搜索到目標節點時通過回溯就可以確定路徑。
2、實現流程
? ? ? ? 依然使用偽代碼對實現流程進行簡要描述：
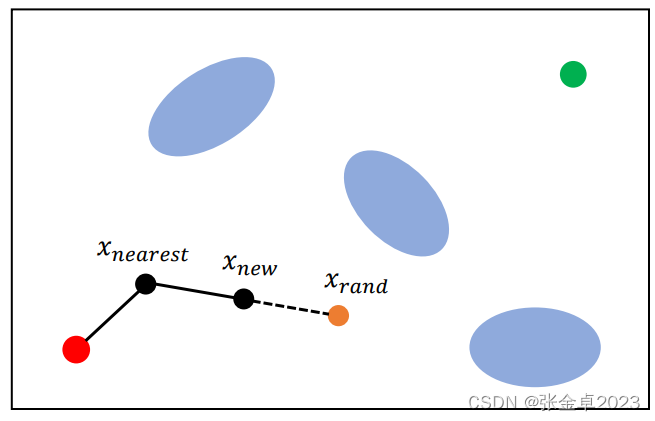
V <- {root}; E <- ?; // 維護集合V和E,分別存放節點和邊，在V中先將初始節點作為根節點放入
for i = 1,...,n doxrand ← SampleFree; // 在freespcace中得到采樣點xrandxnearest ← Nearest(G=(V,E),xrand); // 設置離xrand距離最近的樹節點為xnearestxnew ← steer(xnearest,xrand); // 通過特定的方式將xnearest與xrand進行連接，此處直接設置了一個中間節點，比較經典的方式設置一段弧長if ObtacleFree(xnearest,xrand) then // 進行連線障礙物檢測V ← V∪{xnew}; E ← E∪{xnearest,xnew}; // 檢測通過將邊保存到集合E中
return G={V,E};
?3、總結
? ? ? ? 優點：如果是找尋找兩個特定節點間的路徑，RRT的效率會顯著地優于PRM；
? ? ? ? 缺點：RRT不具備概率完備性，因為它每次都是樹的最近節點連接，如下圖紅色區域中搜索得到的路徑顯然不是最優解。
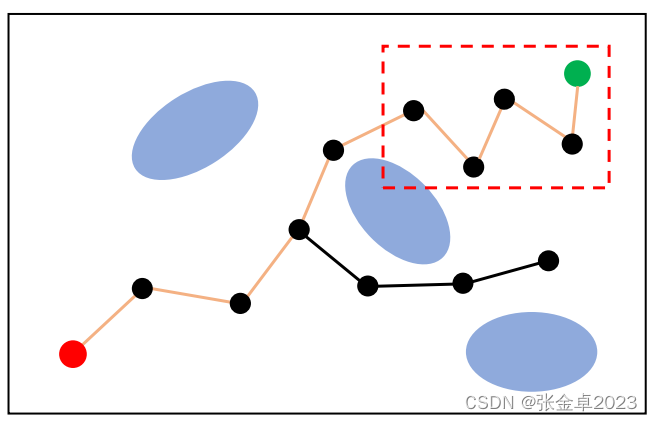
4、改進RRT算法
? ? ? ? 為了解決RRT算法不具備概率完備性的缺陷，后來又提出了多種改進的RRT算法。
①快速搜索隨機圖（RRG）
V <- {root}; E <- ?;
for i = 1,...,n doxrand ← SampleFree; xnearest ← Nearest(G=(V,E),xrand); xnew ← steer(xnearest,xrand);if ObtacleFree(xnearest,xrand) then Xnear ← Near(G=(V,E),xnew,min{γRRG(log(card(V))/card(V)^(1/d),η); // 將xnew附近給定半徑內的所有節點都存入Xnear集合中V ← V∪{xnew}; E ← E∪{xnearest,xnew};foreach xnear in Xnear doif CollisionFree(xnear,xnew) then E ← E∪{xnearest,xnew}; // 將通過碰撞檢測的所有Xnear集合中的節點與xnew的連線都存入集合E中return G={V,E};? ? ? ? 核心思想：不僅僅只是連接xnew和xnearest，將xnew半徑范圍內的所有符合非碰撞條件的節點都連接。
? ? ? ? 雖然RRG使得算法具有概率完備性，但是卻違背了RRT算法提高效率的初衷，因為RRG算法在實現過程中并沒有在維護樹結構，輸出的依然是一個圖，相當于是PRM的學習階段，還要再利用搜索算法進行最優路徑確定。
②基于運動學的快速搜索隨機樹（Kinematic-based RRT）
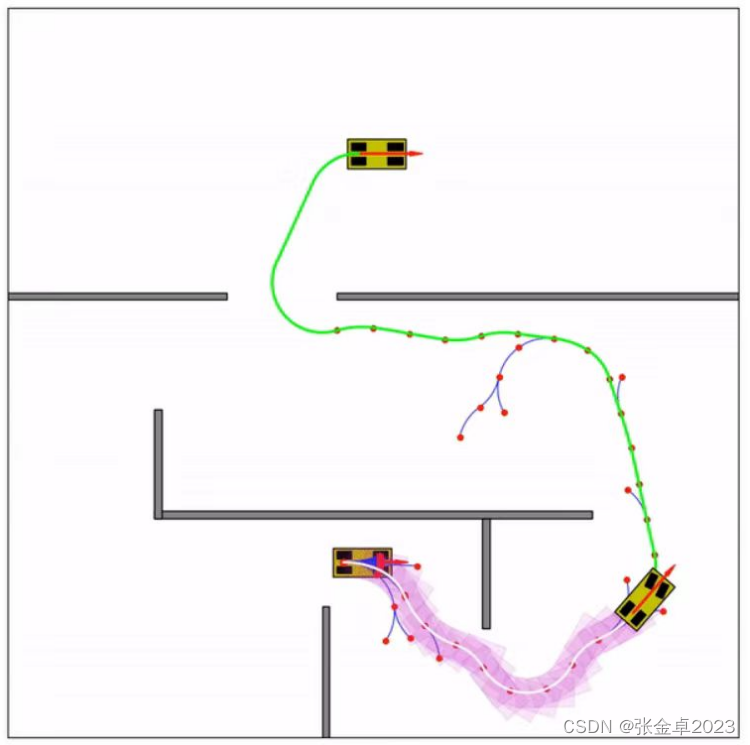
? ? ? ? 核心思想：利用車輛運動學方法在兩個節點之間進行轉向，主要在于RRT偽代碼中xnew獲取步驟的優化。
? ? ? ? 上圖所示是基于杜賓斯規劃（dubins_path_planning）得到的路徑，可以看出在引入車輛運動學方法后，得到的最終路徑是一條較為平滑的曲線。dubins_path_planning的具體介紹在后面會具體介紹。
四、優化的快速搜索隨機數（RRT*）
1、核心思想
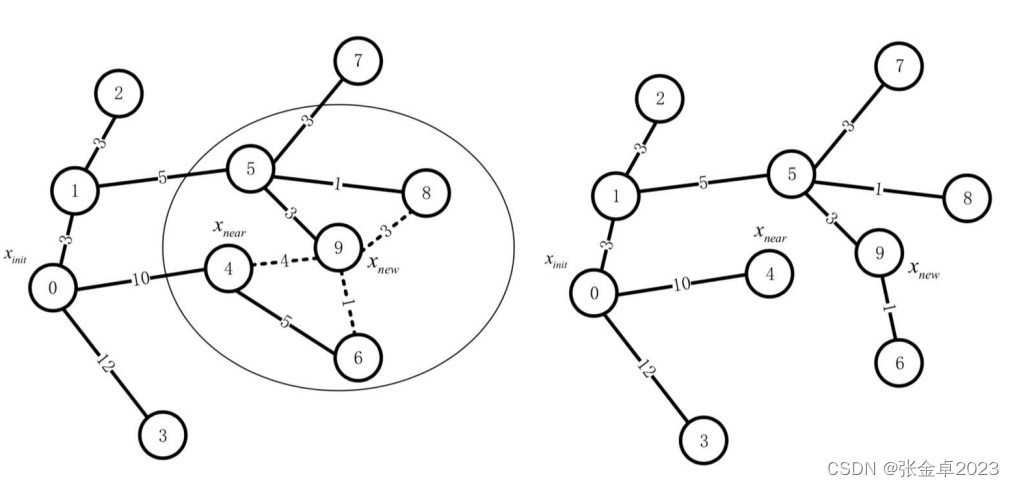
- 與RRG算法相比，RRT*算法維護的是一個樹結構，而不是一個圖，也就是說會在RRG得的圖中刪除掉多余的邊界；
- 與原來的RRT算法相比，RRT*增加了重連的步驟以確保各個節點取得的是最小代價值。
2、實現流程
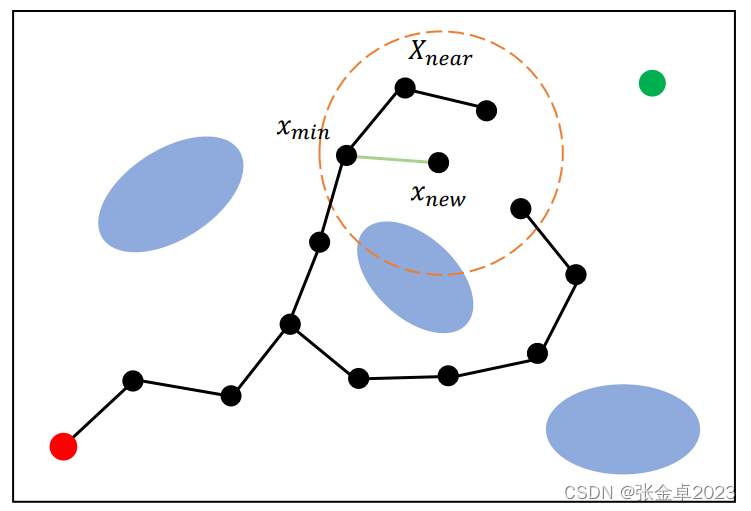
V <- {root}; E <- ?;
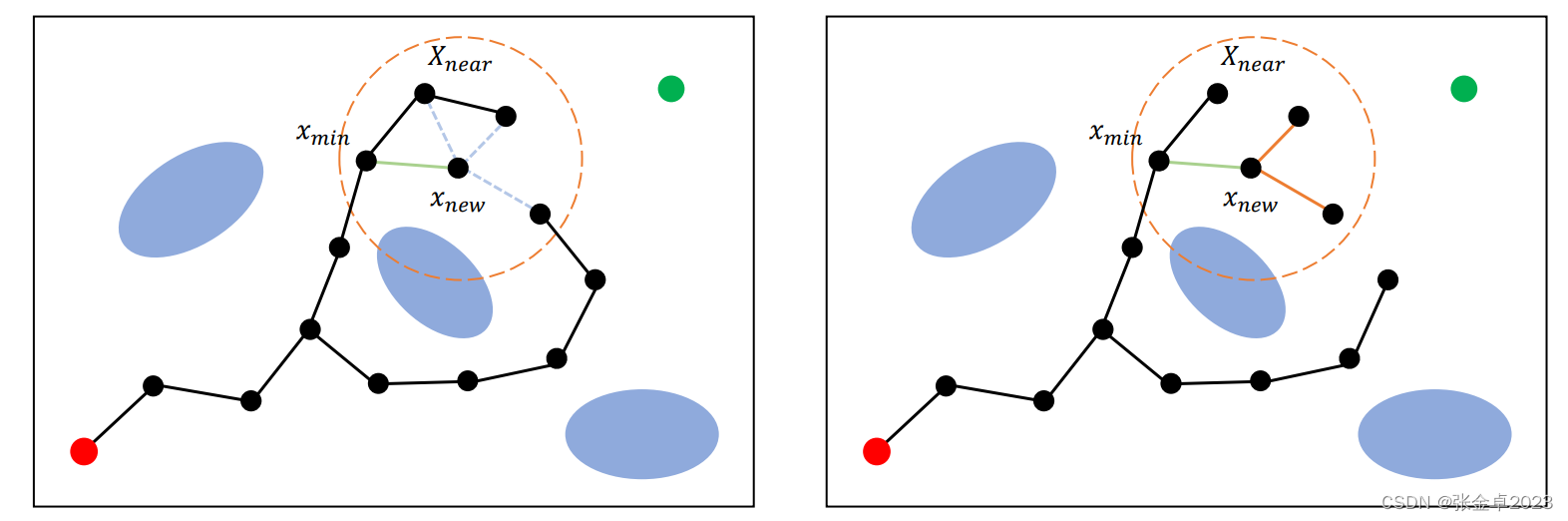
for i = 1,...,n doxrand ← SampleFree; xnearest ← Nearest(G=(V,E),xrand); xnew ← steer(xnearest,xrand);if ObtacleFree(xnearest,xrand) then // 延續RRG的思想先搜索附近的鄰居節點Xnear ← Near(G=(V,E),xnew,min{γRRG(log(card(V))/card(V)^(1/d),η); V ← V∪{xnew};xmin ← xnear; cmin ← Cost(xnearest) + c(Line(xnearest,xnew));// 獲取代價值最小節點foreach xnear in Xnear do if CollisionFree(xnear,xnew) && Cost(xnew) + c(Line(xnearest,xnew)) < c(min) thenxmin ← xnear; cmin ← Cost(xnear) + c(Line(xnearest,xnew))// 對節點進行重連，通過xnew更新總代價值值和路徑foreach xnear in Xnear do if CollisionFree(xnew,xnear) && Cost(xnew) + c(Line(xnew,xnearest)) < Cost(xnear)then xparent ← Parent(xnear);E ← (E\{xparent,xnear}∪{xnew,xnear}) // 在邊集合中刪除xnear到其原父節點xparent的連線，重新加入xnew到xnear的連線
return G = {V,E};
?
)
