一、圖解法求解步驟（只適用于兩個決策變量問題）

三步走

1、全部約束條件 取等 作圖求出可行域
2、做目標函數等值線，確定使目標函數最優化的移動方向
3、平移目標函數等值線，找出最優點，算出最優值。

二、圖解法作圖實例

三、圖解法分析線性規劃幾種解的情況

1、唯一最優解

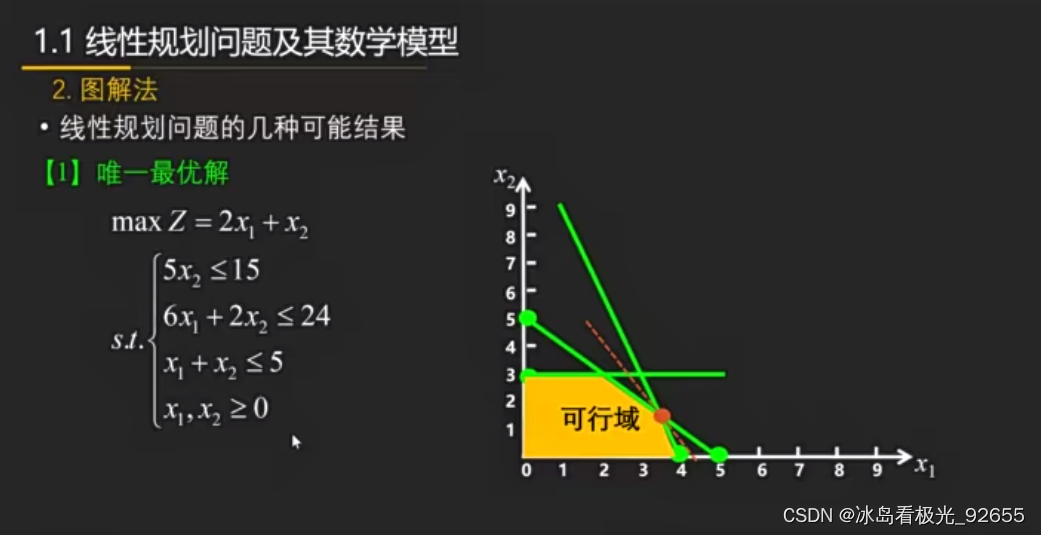
2、無窮多最優解

3、無界解

實際問題中約束條件不足 導致 可行域為無界域

4、無解或無可行解

約束條件矛盾導致 可行域為空集

四、圖解法的幾點啟示

結論：
1、線性規劃解的情況有：唯一最優解、無窮多最優解、無界解、無可行解
2、若線性規劃的可行域存在，則可行域一定是個凸集
3、若線性規劃的最優解存在，則最優解或最優解之一（無窮多解時）一定是可行域的凸集的某個頂點
4、解題思路：找出凸集的頂點，計算其目標函數值，比較即得