集成學習的思想是將若干個學習器(分類器&回歸器)組合之后產生一個新學習器。弱分類器(weak learner)指那些分類準確率只稍微好于隨機猜測的分類器(errorrate < 0.5)。
集成算法的成功在于保證弱分類器的多樣性(Diversity)。而且集成不穩定的算法也能夠得到一個比較明顯的性能提升。
常見的集成學習思想有:Bagging、Boosting、Stacking
為什么需要集成學習
- 弱分類器間存在一定的差異性,這會導致分類的邊界不同,也就是說可能存在錯誤。那么將多個弱分類器合并后,就可以得到更加合理的邊界,減少整體的錯誤率,實現更好的效果;
- 對于數據集過大或者過小,可以分別進行劃分和有放回的操作產生不同的數據子集,然后使用數據子集訓練不同的分類器,最終再合并成為一個大的分類器;
- 如果數據的劃分邊界過于復雜,使用線性模型很難描述情況,那么可以訓練多個模型,然后再進行模型的融合;
- 對于多個異構的特征集的時候,很難進行融合,那么可以考慮每個數據集構建一個分類模型,然后將多個模型融合。
Bagging
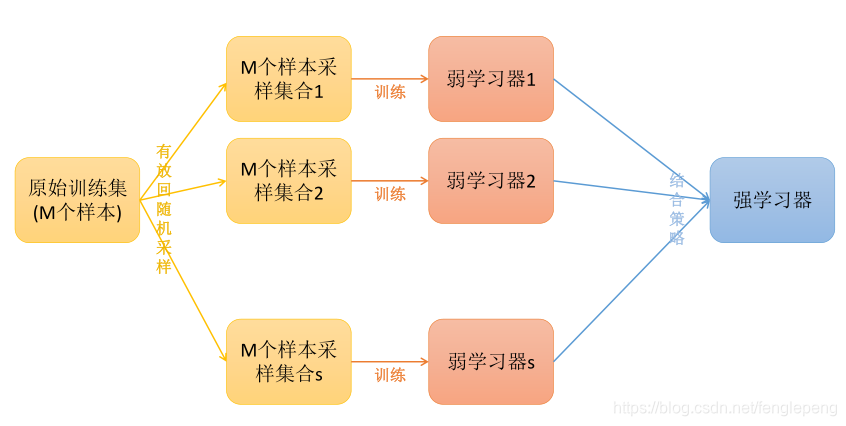
Bagging方法又叫做自舉匯聚法(Bootstrap Aggregating),思想是:在原始數據集上通過有放回的抽樣的方式,重新選擇出S個新數據集來分別訓練S個分類器的集成技術。也就是說這些模型的訓練數據中允許存在重復數據。
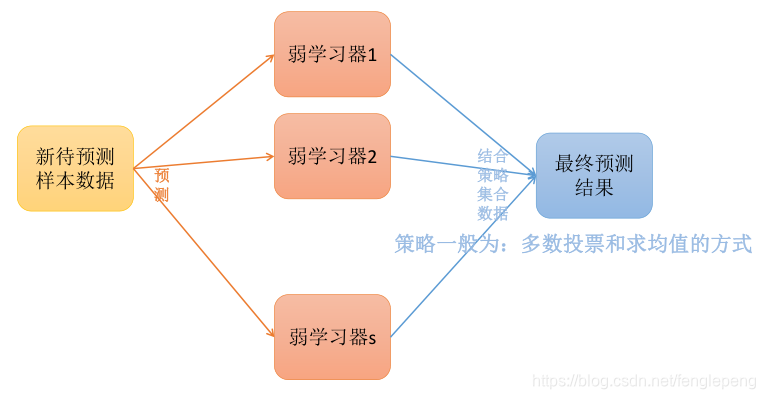
Bagging方法訓練出來的模型在預測新樣本分類的時候,會使用多數投票或者求均值的方式來統計最終的分類結果。
Bagging方法的弱學習器可以是基本的算法模型,eg: Linear、Ridge、Lasso、Logistic、Softmax、ID3、C4.5、CART、SVM、KNN等。
備注:Bagging方式是有放回的抽樣,并且每個子集的樣本數量必須和原始樣本數量一致,但是子集中允許存在重復數據。
Bagging訓練過程
Bagging預測過程
隨機森林(Random Forest)
在Bagging策略的基礎上修改之后的算法:
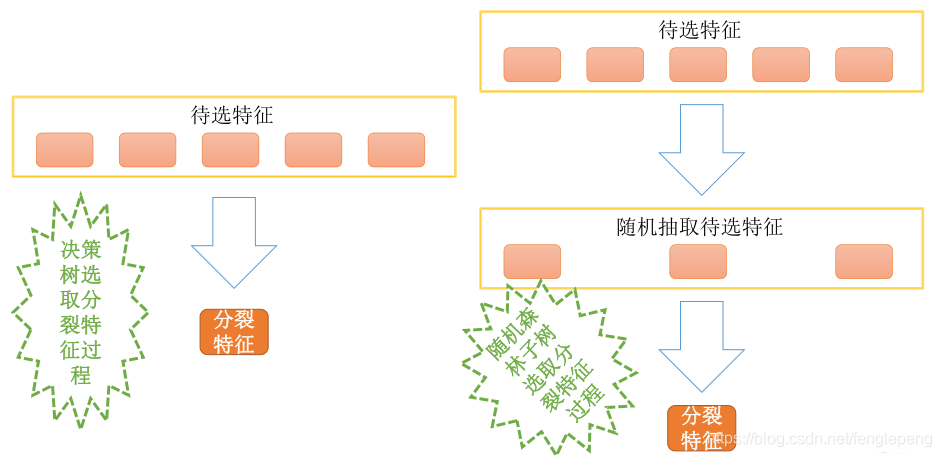
- 從樣本集中用Bootstrap采樣選出n個樣本。
- 從所有屬性中隨機選擇K個屬性,選擇出最佳分割屬性作為節點創建決策樹。
- 重復以上兩步m次,即建立m棵決策樹。
- 這m棵決策樹形成隨機森林,通過投票表決結果決定數據屬于哪一類。如下圖:
RF的推廣算法
RF算法在實際應用中具有比較好的特性,應用也比較廣泛,主要應用在:分類、回歸、特征轉換、異常點檢測等。常見的RF變種算法如下:
- Extra Tree
- Totally Random Trees Embedding(TRTE)
- Isolation Forest
RF的推廣算法:Extra Tree
ET是RF的一個變種,原理基本相同,區別在于:
- RF會隨機采樣作為決策樹的訓練集,而ET每個決策樹采用原始數據集訓練。
- RF在選擇劃分特征點的時候會和傳統決策樹一樣,會基于信息增益、信息增益率、基尼系數、均方差等原則來選擇最有特征值;而ET會隨機的選擇一個特征值來劃分決策樹。
ET因為是隨機選擇特征值的劃分點,這樣會導致決策樹的規模一般大于RF所生成的決策樹。也就是說ET模型的方差相對于RF進一步減少。在某些情況下,ET的泛化能力比RF的強。
RF的推廣算法:Totally Random Trees Embedding(TRTE)
TRTE是一種非監督的數據轉化方式。將低維的數據集映射到高維,從而讓映射到高維的數據更好的應用于分類回歸模型。
TRTE算法的轉化過程類似RF算法的方法,建立T個決策樹來擬合數據。當決策樹構建完成之后,數據集里面的每個數據在T個決策樹中葉子節點的位置就定下來了,將位置信息轉化為向量就完成了特征轉化的操作。
案例:有3棵決策樹,每棵決策樹有5個葉子節點,某個數據x劃分到第一個決策樹的第3個葉子節點,第二個決策樹的第一個葉子節點,第三個決策樹的第第五個葉子節點,那么最終的x映射特征編碼為:(0,0,1,0,0, 1,0,0,0,0, 0,0,0,0,1)

RF的推廣算法:Isolation Forest(IForest)
IForest是一種異常點檢測算法,使用類似RF的方式來檢測異常點;IForest算法和RF算法的區別在于:
- 在隨機采樣的過程中,一般只需要少量數據即可。
- 在進行決策樹構建的過程中,IForest算法會隨機選擇一個劃分特征,并對劃分特征隨機選擇一個劃分閾值。
- IForest算法構建的決策樹一般深度max_depth是比較小的。
區別原因
目的是異常點檢測,所以只要能夠區別異常的即可,不需要大量數據,同時也不需要建立太大規模的決策樹。
對于異常點的判斷。是將測試樣本X擬合到T棵決策樹上。計算在每棵樹上該樣本的葉子節點的深度H。從而計算出平均深度h;然后使用公式計算樣本點X的異常概率值,p(s,m)的取值范圍是[0,1],越接近1,則是異常點的概率越大。
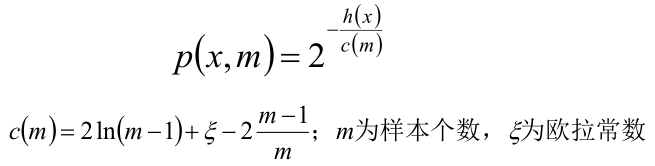
RF隨機森林總結
在隨機森林的構建過程中,由于各棵樹之間是沒有關系的,相互獨立;在構建的過程中,構建第m棵字數的時候,不考慮前面的m-1棵樹。
思考:
如果在構建第m棵子樹的時候,考慮到前m-1棵子樹的結果,會不會對最終結果產生有益的影響?
各個決策樹組成隨機森林后,在形成最終結果的時候能不能給定一種既定的決策順序呢?(也就是那顆子樹先進行決策、那顆子樹后進行決策)
RF的主要優點
- 訓練可以并行化,對于大規模樣本的訓練具有速度的優勢。
- 由于進行隨機選擇決策樹劃分特征列表,這樣在樣本維度比較高的時候,仍具有比較高的訓練性能。
- 給出各個特征的重要性列表。
- 由于存在隨機抽樣,訓練出來的模型方差小,泛化能力強。
- RF實現簡單。
- 對于部分特征的缺失不敏感。
RF的主要缺點
- 在某些噪聲比較大的特征上,RF模型容易陷入過擬合。
- 取值比較多的劃分特征對RF決策樹會產生更大的影響,從而有可能影響模型的效果。
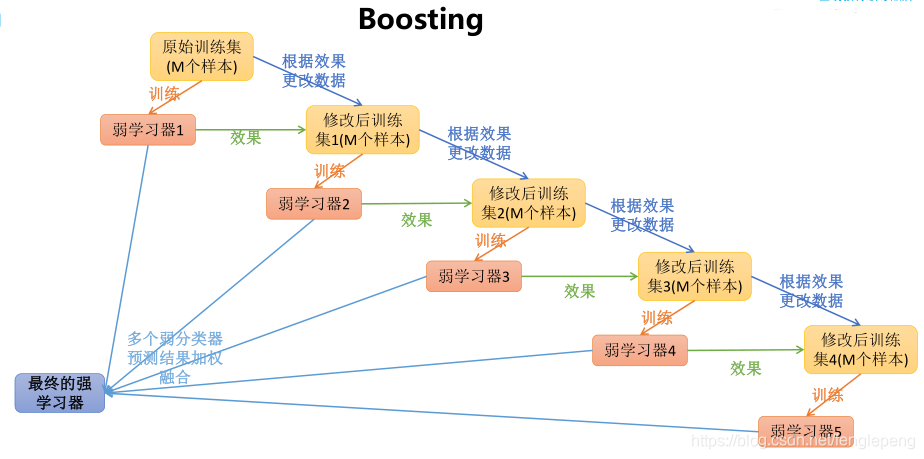
Boosting
提升學習(Boosting)是一種機器學習技術,可以用于回歸和分類的問題,它每一步產生弱預測模型(如決策樹),并加權累加到總模型中。如果每一步的弱預測模型的生成都是依據損失函數的梯度方式,那么就稱為梯度提升(Gradient boosting)。
百度百科:Boosting是一種框架算法,主要是通過對樣本集的操作獲得樣本子集,然后用弱分類算法在樣本子集上訓練生成一系列的基分類器。
提升技術的意義:如果一個問題存在弱預測模型,那么可以通過提升技術的方法得到一個強預測模型。(強預測模型由若干個弱預測模型累加而成)。
常見的模型有:Adaboost、Gradient Boosting(GBT/GBDT/GBRT)。
AdaBoost
AdaBoost算法原理
Adaptive Boosting是一種迭代算法。每輪迭代中會在訓練集上產生一個新的學習器,然后使用該學習器對所有樣本進行預測,以評估每個樣本的重要性(Informative)。換句話來講就是,算法會為每個樣本賦予一個權重,每次用訓練好的學習器標注/預測各個樣本,如果某個樣本點被預測的越正確,則將其權重降低;否則提高樣本的權重。權重越高的樣本在下一個迭代訓練中所占的比重就越大,也就是說越難區分的樣本在訓練過程中會變得越重要;
整個迭代過程直到錯誤率足夠小或者達到一定的迭代次數為止。
可以看見,每一次學習后,被誤分的樣本具有的更高的權重,這權重在下一次構建學習器的時候產生影響(對樣本集的影響構建成多個樣本子集)。
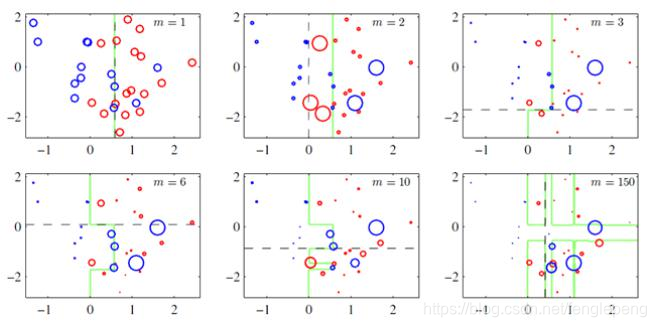
樣本加權
下面圖片中表現了樣本加權的過程。標記變大的就是前一次迭代中誤判斷的樣本點,標記越大說明權重越高。
Adaboost算法
Adaboost算法將基分類器的線性組合作為強分類器,同時給分類誤差率較小的基本分類器以大的權值,給分類誤差率較大的基分類器以小的權重值;構建的線性組合為
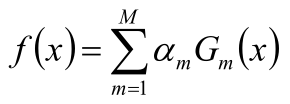
最終分類器是在線性組合的基礎上進行Sign函數轉換(取數字n的符號,大于0返回1,小于0返回-1,等于0返回0):
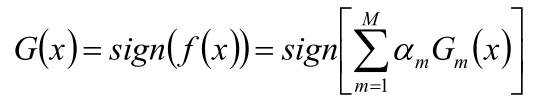
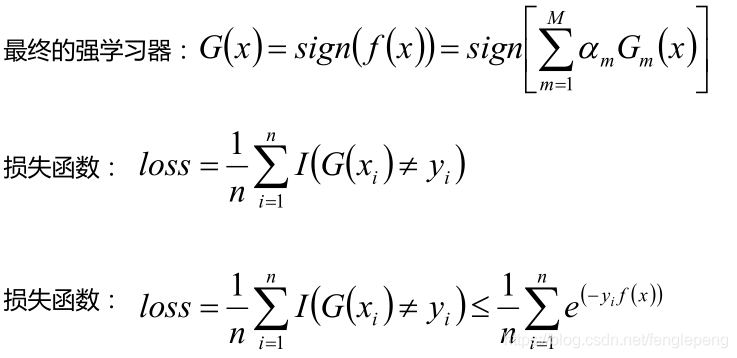
 。
。
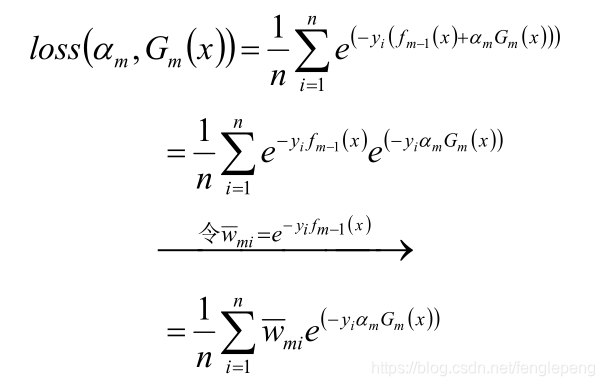

Adaboost算法構建過程一


Adaboost算法的直觀理解








AdaBoost的優缺點
AdaBoost的優點如下:
- 可以處理連續值和離散值;
- 模型的魯棒性比較強;
- 解釋強,結構簡單。
AdaBoost的缺點如下:
- 對異常樣本敏感,異常樣本可能會在迭代的過程中獲得比較高的權重值,最終影響模型效果。
梯度提升決策樹GBDT
GBDT也是Boosting算法的一種,但是和AdaBoost算法不同;區別如下:AdaBoost算法是利用前一輪的弱學習器的誤差來更新樣本權重值,然后一輪一輪的迭代;GBDT也是迭代,但是GBDT要求弱學習器必須是CART模型(決策樹),而且GBDT在模型訓練的時候,是要求模型預測的樣本損失盡可能的小。
別名:GBT(Gradient Boosting Tree)、GTB(Gradient Tree Boosting)、GBRT(Gradient Boosting Regression Tree)、GBDT(Gradient Boosting Decison Tree)、MART(Multiple Additive Regression Tree)

GBDT是由三個部分組成:DT(Regression Decistion Tree)、GB(Gradient Boosting)和 Shrinking(衰減)。所有樹的結果累加起來就是最終結果。
GBDT直觀理解
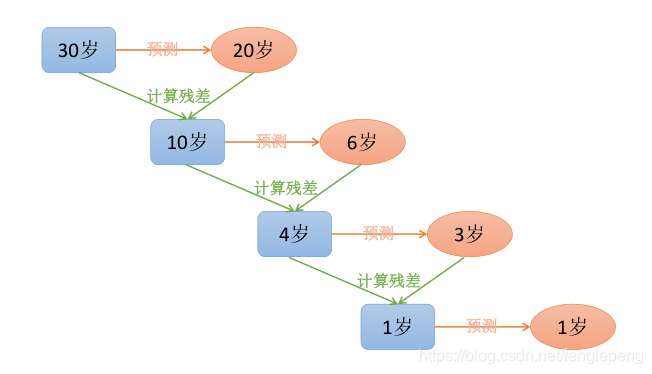
當給定步長時候,給定一個步長step,在構建下一棵樹的時候使用step*殘差值作為輸入值,這種方式可以減少過擬合的發生
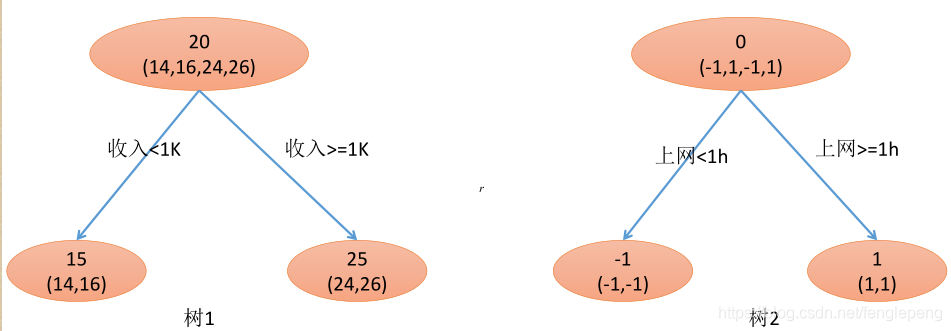
迭代決策樹與隨機森林的區別:
- 隨機森林使用抽取不同樣本構建不同的子樹,也就是說第m棵樹的構建與第m-1棵樹是沒有關系的。
- 迭代決策樹在構建子樹的時候,使用之前的子樹構建結果后形成的殘差作為輸入數據構建下一個子樹,最終預測時候按照子樹的構建的順序進行預測,并將預測結果相加。
GBDT算法原理
給定輸入向量X和輸出變量Y組成的若干訓練樣本( ,
),(
,
)......(
,
),目標是找到近似函數F(X),使得損失函數L(Y,F(X))的損失值最小。
L損失函數一般采用最小二乘損失函數或者絕對值損失函數
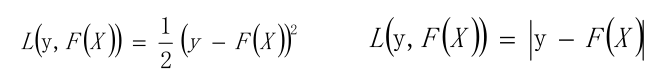
最優解為:

假定F(X)是一族最優基函數f i (X)的加權和:

以貪心算法的思想擴展得到Fm(X),求解最優f
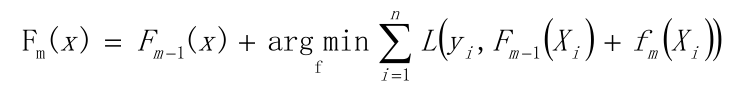
以貪心法在每次選擇最優基函數f時仍然困難,使用梯度下降的方法近似計算
給定常數函數F 0 (X)
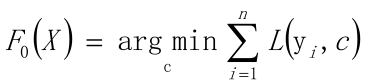

GBDT回歸算法和分類算法的區別
唯一的區別在于選擇不同的損失函數。
回歸算法中選擇的損失函數是均方差(最小二乘)或者是絕對值誤差。分類算法中一般的損失函數選擇對數函數來表示。Bagging、Boosting的區別
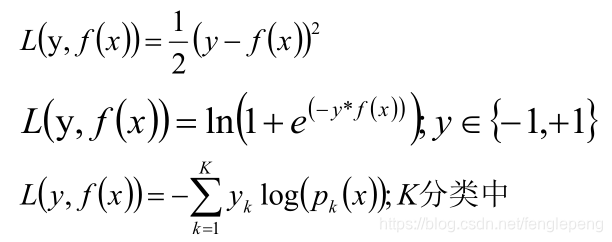
GBDT的優缺點
GBDT的優點如下:
- 可以處理連續值和離散值;
- 在相對少的調參情況下,模型的預測效果也會不錯;
- 模型的魯棒性比較強。
GBDT的缺點如下:
- 由于弱學習器之間存在關聯關系,難以并行訓練模型
Bagging、Boosting的區別
- 樣本選擇:Bagging算法是有放回的隨機采樣;Boosting算法是每一輪訓練集不變,只是訓練集中的每個樣例在分類器中的權重發生變化,而權重根據上一輪的分類結果進行調整;
- 樣例權重:Bagging使用隨機抽樣,樣例的權重;Boosting根據錯誤率不斷的調整樣例的權重值,錯誤率越大則權重越大;
- 預測函數:Bagging所有預測模型的權重相等;Boosting算法對于誤差小的分類器具有更大的權重。
- 并行計算:Bagging算法可以并行生成各個基模型;Boosting理論上只能順序生產,因為后一個模型需要前一個模型的結果;
- Bagging是減少模型的variance(方差);Boosting是減少模型的Bias(偏度)。
- Bagging里每個分類模型都是強分類器,因為降低的是方差,方差過高需要降低是過擬合;Boosting里每個分類模型都是弱分類器,因為降低的是偏度,偏度過高是欠擬合。我們認為方差越大的模型越容易過擬合:假設有兩個訓練集A和B,經過A訓練的模型Fa與經過B訓練的模型Fb差異很大,這意味著Fa在類A的樣本集合上有更好的性能,而Fb在類B的訓練樣本集合上有更好的性能,這樣導致在不同的訓練集樣本的條件下,訓練得到的模型的效果差異性很大,很不穩定,這便是模型的過擬合現象,而對于一些弱模型,它在不同的訓練樣本集上 性能差異并不大,因此模型方差小,抗過擬合能力強,因此boosting算法就是基于弱模型來實現防止過擬合現象。

- Bagging對樣本重采樣,對每一輪的采樣數據集都訓練一個模型,最后取平均。由于樣本集的相似性和使用的同種模型,因此各個模型的具有相似的bias和variance;
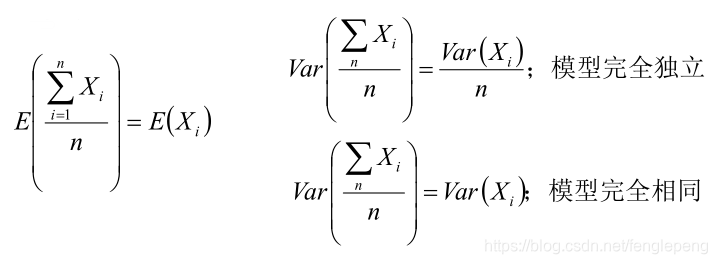
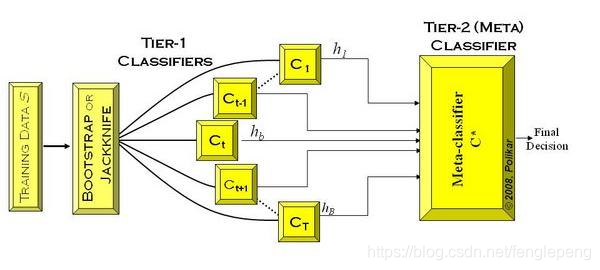
Stacking
Stacking是指訓練一個模型用于組合(combine)其它模型(基模型/基學習器)的技術。即首先訓練出多個不同的模型,然后再以之前訓練的各個模型的輸出作為輸入來新訓練一個新的模型,從而得到一個最終的模型。一般情況下使用單層的Logistic回歸作為組合模型。
?


)






)
)








