機器學習之拉格朗日乘子法和 KKT

有約束的最優化問題

最優化問題一般是指對于某一個函數而言，求解在其指定作用域上的全局最小值問題，一般分為以下三種情況(備注：以下幾種方式求出來的解都有可能是局部極小值，只有當函數是凸函數的時候，才可以得到全局最小值)：

1、無約束問題：求解方式一般為梯度下降法、牛頓法、坐標軸下降法等；

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $\min f(x)$

2、等式約束條件：求解方式一般為拉格朗日乘子法

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? $\begin{center} \min f(x) \\s.t.\ \ h_k(x)=0 \ \ \ k=1, 2, \dots, p \\F(x, \alpha )=f(x)+\sum_{k=1}^p\alpha_kh_k(x)\end{center}$

3、不等式約束條件：求解方式一般為KKT條件

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $\begin{center} \min f(x) \\ s.t.\ \ \ \ \ h_k(x)=0 \ \ \ \ \ \ k=1, 2, \dots, p \\\ \ \ \ \ \ \ \ \ g_j(x) \le 0 \ \ \ \ \ \ j=1, 2, \dots, q \\L(x, \alpha, \beta)=f(x)+\sum_{k=1}^p\alpha_kh_k(x)+\sum_{j=1}^q\beta_jg_j(x) \end{center}$

拉格朗日乘子法

拉格朗日乘子法就是當我們的優化函數存在等值約束的情況下的一種最優化求解方式；

其中參數α被稱為拉格朗日乘子，要求α不等于0

$\begin{center} \min f(x) \\s.t.\ \ h_k(x)=0, \ \ \ k=1, 2, \dots, p \\F(x, \alpha )=f(x)+\sum_{k=1}^{p}\alpha_kh_k(x),\ \ \ \alpha_k \neq 0\end{center}$

假設現在有一個二維的優化問題

畫出圖像加深理解

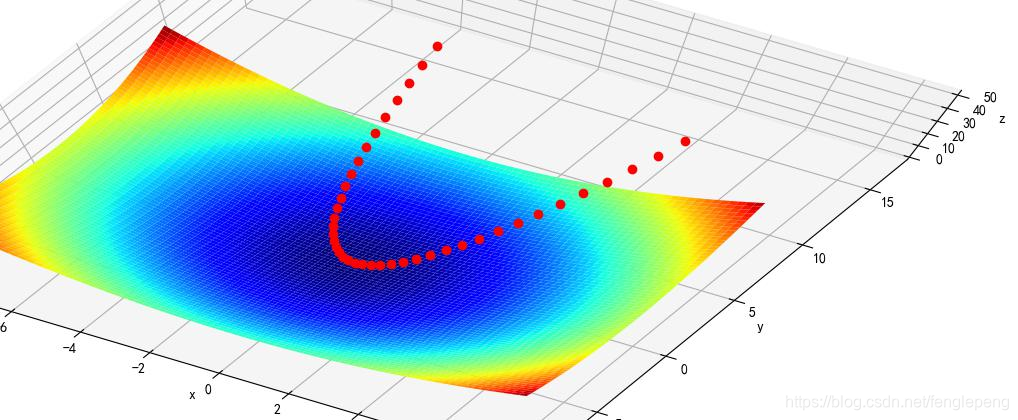
數學證明可參考鏈接:https://wenku.baidu.com/view/ac56710e2e3f5727a5e962a7.html

對偶問題

$\underset{\beta }{min}\ \underset{x}{min}\ L(x,\beta)=\underset{x}{min}\ \underset{\beta }{max}\ L(x,\beta)$

在優化問題中，目標函數f(x)存在多種形式，如果目標函數和約束條件都為變量x的線性函數，則稱問題為線性規劃；如果目標函數為二次函數，則稱最優化問題為二次規劃；如果目標函數或者約束條件為非線性函數，則稱最優化問題為非線性優化。每個線性規劃問題都有一個對應的對偶問題。對偶問題具有以下幾個特性：

對偶問題的對偶是原問題；
無論原始問題是否是凸的，對偶問題都是凸優化問題；
對偶問題可以給出原始問題的一個下界；
當滿足一定條件的時候，原始問題和對偶問題的解是完美等價的。

KKT條件

KKT條件是泛拉格朗日乘子法的一種形式；主要應用在當我們的優化函數存在不等值約束的情況下的一種最優化求解方式；KKT條件即滿足不等式約束情況下的條件。

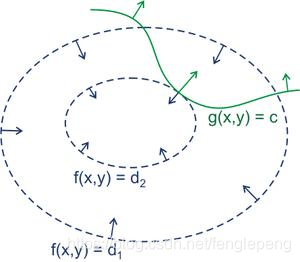
$\begin{center} \min f(x) \\ s.t.\ \ \ \ \ h_k(x)=0 \ \ \ \ \ \ k=1, 2, \dots, p \\\ \ \ \ \ \ \ \ \ g_j(x) \le 0 \ \ \ \ \ \ j=1, 2, \dots, q \\L(x, \alpha, \beta)=f(x)+\sum_{k=1}^p\alpha_kh_k(x)+\sum_{j=1}^q\beta_j g_j(x) ,\ a_k\neq 0,\beta_j \geq 0\end{center}$

可行解必須在約束區域g(x)之內，由圖可知可行解x只能在g(x)<0和g(x)=0的區域取得；

當可行解x在g(x)<0的區域中的時候，此時直接極小化f(x)即可得到；

當可行解x在g(x)=0的區域中的時候，此時直接等價于等式約束問題的求解。

KKT條件理解

當可行解在約束內部區域的時候，令β=0即可消去約束。

對于參數β的取值而言，在等值約束中，約束函數和目標函數的梯度只要滿足平行即可，而在不等式約束中，若β≠0，則說明可行解在約束區域的邊界上，這個時候可行解應該盡可能的靠近無約束情況下的解，所以在約束邊界上，目標函數的負梯度方向應該遠離約束區域朝無約束區域時的解，此時約束函數的梯度方向與目標函數的負梯度方向應相同；從而可以得出β>0。

對偶問題的直觀理解：最小的里面的那個最大的要比最大的那個里面的最小的大；從而就可以為原問題引入一個下界。

KKT 案例

這里利用該KKT條件滿足對偶條件：

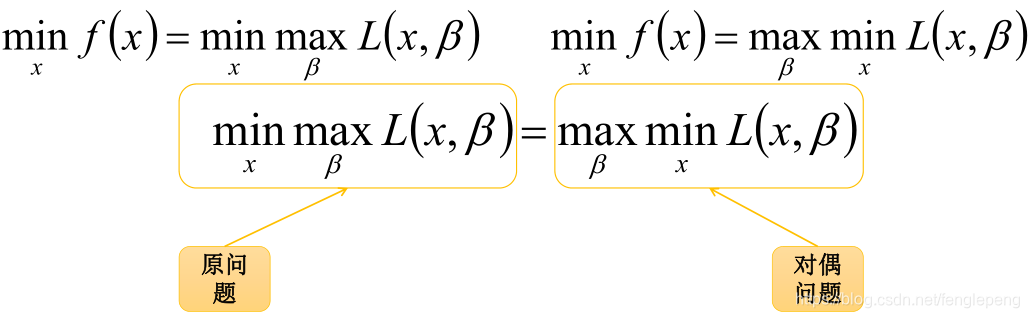
對偶問題的直觀理解：最小的里面的那個最大的要比最大的那個里面的最小的大；從而就可以為原問題引入一個下界

KKT條件總結

KKT條件為下列五個

拉格朗日取得可行解的充要條件；
將不等式約束轉換后的一個約束，稱為松弛互補條件；
初始的約束條件；
初始的約束條件；
不等式約束需要滿足的條件。

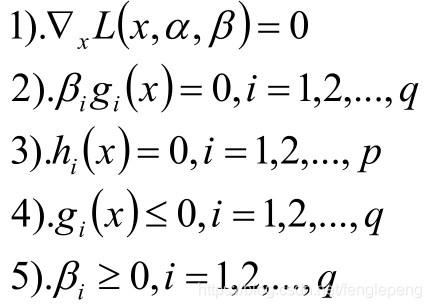
本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/454343.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/454343.shtml
英文地址，請注明出處：http://en.pswp.cn/news/454343.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！