機器學習之聚類概述

什么是聚類

聚類就是對大量未知標注的數據集，按照數據內部存在的數據特征將數據集劃分為多個不同的類別，使類別內的數據比較相似，類別之間的數據相似度比較小；屬于無監督學習。

聚類算法的重點是計算樣本項之間的相似度，有時候也稱為樣本間的距離。

和分類算法的區別：

分類算法是有監督學習，基于有標注的歷史數據進行算法模型構建
聚類算法是無監督學習，數據集中的數據是沒有標注的

有個成語到“物以類聚”，說的就是聚類的概念。直白來講，就是把認為是一類的物體聚在一起，也就是歸為一類（聚在一起的叫一個簇）。

聚類的思想

給定一個有M個對象的數據集，構建一個具有k個簇的模型，其中k<=M（這是肯定的，不可能有3個對象，我劃分成4個類吧）。滿足以下條件：

每個簇至少包含一個對象
每個對象屬于且僅屬于一個簇
將滿足上述條件的k個簇成為一個合理的聚類劃分

總的一個思路就是：對于給定的類別數目k，首先給定初始劃分，通過迭代改變樣本和簇的隸屬關系，使的每次處理后得到的劃分方式比上一次的好 (總的數據集之間的距離和變小了)

相似度/距離公式

上面一直提到什么相似度或距離，特征空間中兩個實例點的距離就是兩個實例點相似程度的反映。我們也經常用到歐式距離，除此之外還有哪些，這里羅列一些相關公式，因為好多不常用，所以只做簡要介紹，或者僅僅提及一下。

1. 閔可夫斯基距離(Minkowski)，也叫范式

對于兩個 n 維的數據 X,Y?

$dist(X,Y)=\sqrt[^{^{^{^p}}}]{\sum_{i=1}^n|x_i - y_i|^p}$ ?這里 ? $p \geq1$

也就是先求各維度的差值，然后把這些差值都取 p 次方，接著累加起來，最后把累加的結果開p次方。

（1）當 p=1 p=1p=1 時，稱為曼哈頓距離（ Manhattan distance，也稱為曼哈頓城市距離），也叫1范式，即

$M\_dist = \sum_{i=1}^n |x_i - y_i|$

以兩維的數據為例：

?¨è?é??￥????è?°

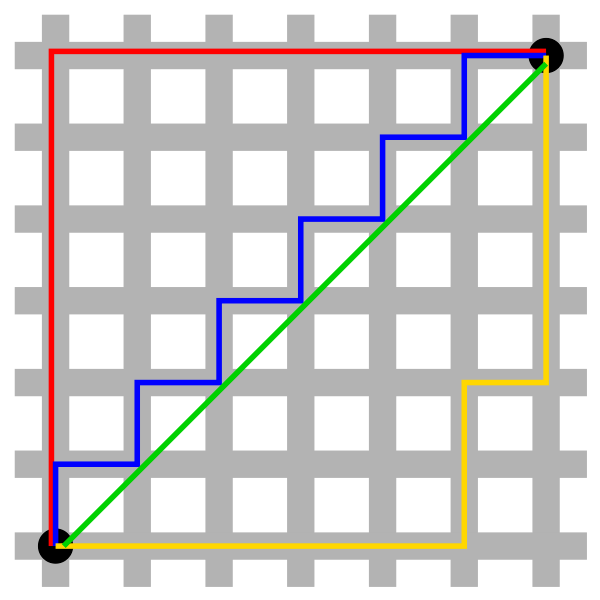
上面的圖就像我們的城市公路，比如說從左下角到右上角，我們可以按紅線（就是兩點間的曼哈頓距離）、藍線或黃線走，最終都可等效成紅線。而綠線就是下面說的歐氏距離。

（2）當 p=2 p=2p=2 時，稱為歐氏距離 (Euclidean distance) ，也叫2范式，即

$E\_dist=\sqrt{\sum_{i=1}^n|x_i - y_i|^2}$

（3）當 p=∞? 時，稱為切比雪夫距離(Chebyshev distance)

$C\_dist=\sqrt[^{^{^{^\infty}}}]{\sum_{i=1}^n|x_i - y_i|^\infty}= \max _i(|x_i - y_i |)$

也就是上圖中，如果橫軸的差值大于縱軸的差值，則就為紅線中的橫線部分；反之就是縱線部分。即，只關心主要的，忽略次要的。

2 . 標準化歐式距離(Standardized Euclidean Distance)

$X^* = \frac{X-\bar{X}}{s}$

這是進行標準化，在數據處理時經常用到。s 表示方差， $s=\sqrt{\frac{\sum_{i=1}^n ( s_i - \bar{s})}{n}}s$

標準的歐式距離? $\quad S\_E\_D = \sqrt{\sum_{i=1}^n \left( \frac{x_i -y_i}{s_i} \right)}$

3 . 夾角余弦相似度(Cosine)

$a = (x_{11},x_{12},...,x_{1n}), b = (x_{21},x_{22},...,x_{2n})$
$\cos(\theta) = \frac{\sum_{k=1}^n x_{1k}x_{2k}}{\sqrt{\sum_{k=1}^n x_{1k}^2}*\sqrt{\sum_{k=1}^n x_{1k}^2}} = \frac{a^T \cdot b}{|a||b|}$

其實就是利用了我們中學所學的余弦定理。

4 . KL距離(相對熵)
$D(P||Q)=\sum_x P(x) \log \left( \frac{P(x)}{Q{x}} \right)$

KL距離在信息檢索領域，以及自然語言方面有重要的運用。具體內容可以參考《【ML算法】KL距離》

5 . 杰卡德相似系數(Jaccard)

$J(A,B)=\frac{|A \cap B|}{A \cup B}$

目標檢測中，經常遇到的IOU，就是這種形式。

$dist(A,B)=1-J(A,B)=\frac{|A \cup B|-|A \cap B|}{|A \cup B|}$

很顯然，杰卡德距離是用兩個集合中不同元素占所有元素的比例來衡量兩個集合的區分度。

6 . Pearson相關系數

$\rho _{XY} = \frac{Cov(X,Y)}{\sqrt{D(X)} \sqrt{D(Y)}} = \frac{E[(X-E(X))(Y-E(Y))]}{\sqrt{D(X)} \sqrt{D(Y)}}=\frac{\sum_{i=1}^n (X_i-\mu_X)(Y_i-\mu_Y)}{\sqrt{\sum_{i=1}^n(X_i-\mu_X)^2}*\sqrt{\sum_{i=1}^n(Y_i-\mu_Y)^2}}$

$dist(X,Y)=1-\rho_{XY}$ ? ??

Pearson相關系數是統計學三大相關系數之一，具體內容可以參考《如何理解皮爾遜相關系數（Pearson Correlation Coefficient）？》

常見聚類算法

常見的算法，按照不同的思想可進行以下劃分，當然還會有一些相應的優化算法，隨后的博客也會一一介紹。

?¨è?é??￥????è?°

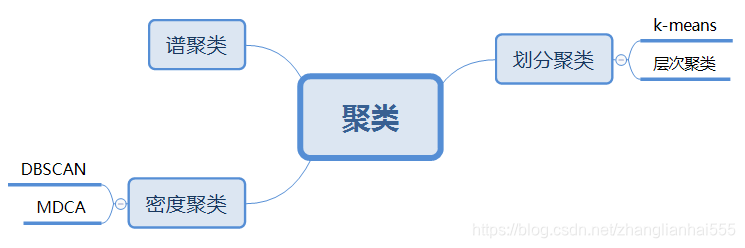
實際中，用的比較多的是劃分聚類，尤其k-means。在古典目標識別中，經常用到Selective Search（選擇搜索）這種圖像bouding boxes提取算法，本質就是層次聚類。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/454347.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/454347.shtml
英文地址，請注明出處：http://en.pswp.cn/news/454347.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！