簡介

邏輯回歸算法是一種簡單但功能強大的二元線性分類算法。需要注意的是，盡管"邏輯回歸"名字帶有“回歸”二字，但邏輯回歸是一個分類算法，而不是回歸算法。
我認為，邏輯回歸算法功能強大的原因，更在于，它不僅僅可以預測類別標簽，而且還可以預測類別的概率。
比如說，使用邏輯回歸預測天氣，不僅僅可以預測某一天是否會下雨，還可以給出下雨的概率。類似地，也可以使用邏輯回歸算法來預測癥狀給定的情況下患者患有某種疾病的概率，這也是邏輯回歸在醫學領域廣受歡迎的原因。

邏輯回歸與條件概率

邏輯回歸是一個二元分類概率模型。下面我們主要了解一下邏輯回歸背后的主要機制。
$p$:感興趣事件發生的概率(所謂感興趣，正是我們想要預測的事件，比如患者在出現某些癥狀時患病的概率。)
幾率(odds):是一個事件發生可能性的度量。數學表達式為:$\frac{p}{1?p}$.
logit 函數:logit函數是幾率(odds)的對數函數:
$logit(p)=\log \frac{p}{1?p}$
這里的log是自然對數。logit函數的輸入即p是一個介于0-1之間的正數，輸出即logit§為任意實數。
那如何將這里的輸出將我們的數據相聯系起來呢?
我們假設我們的輸出即logit§與每一個樣本的特征值$x_1{x}_2{x}_3...x_m$的加權($w^T$)和加偏置頂存在線性關系，即：
$logit(p)=w_1{x}_1+w_2{x}_2+......+w_m{x}_m+b={\sum }_{j=1}^m{w}_j{x}_j+b=w^{T}x+b$
當我們真正感興趣的是條件概率$p$,即在給定一個樣本特征的前提下求解類別標簽為1的概率。
通過logit函數，我們可以將條件概率p映射為一個實數。那反過來，我們要求p的話呢？所以，我們可以根據logit函數求解出它的逆函數。
logit函數的逆函數通常稱為logistic sigmoid函數。由于這個函數具有S形狀，因此有時也簡稱為sigmoid函數：
$\sigma (z)=\frac{1}{1=e^{?z}}$
這里z是凈輸入，為樣本的加權和加偏置頂：
$z=w^{T}x+b$

繪制sigmoid函數

import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):return 1.0/(1.0+np.exp(-z))
z=np.arange(-7,7,0.1)
sigma_z=sigmoid(z)
plt.plot(z,sigma_z)
plt.axvline(0.0,color='k')
plt.ylim(-0.1,1.1)
plt.xlabel('z')
plt.ylabel('$\sigma(z)$')
plt.yticks([0.0,0.5,1.0])
ax=plt.gca()
ax.yaxis.grid(True)
plt.tight_layout()
plt.show()

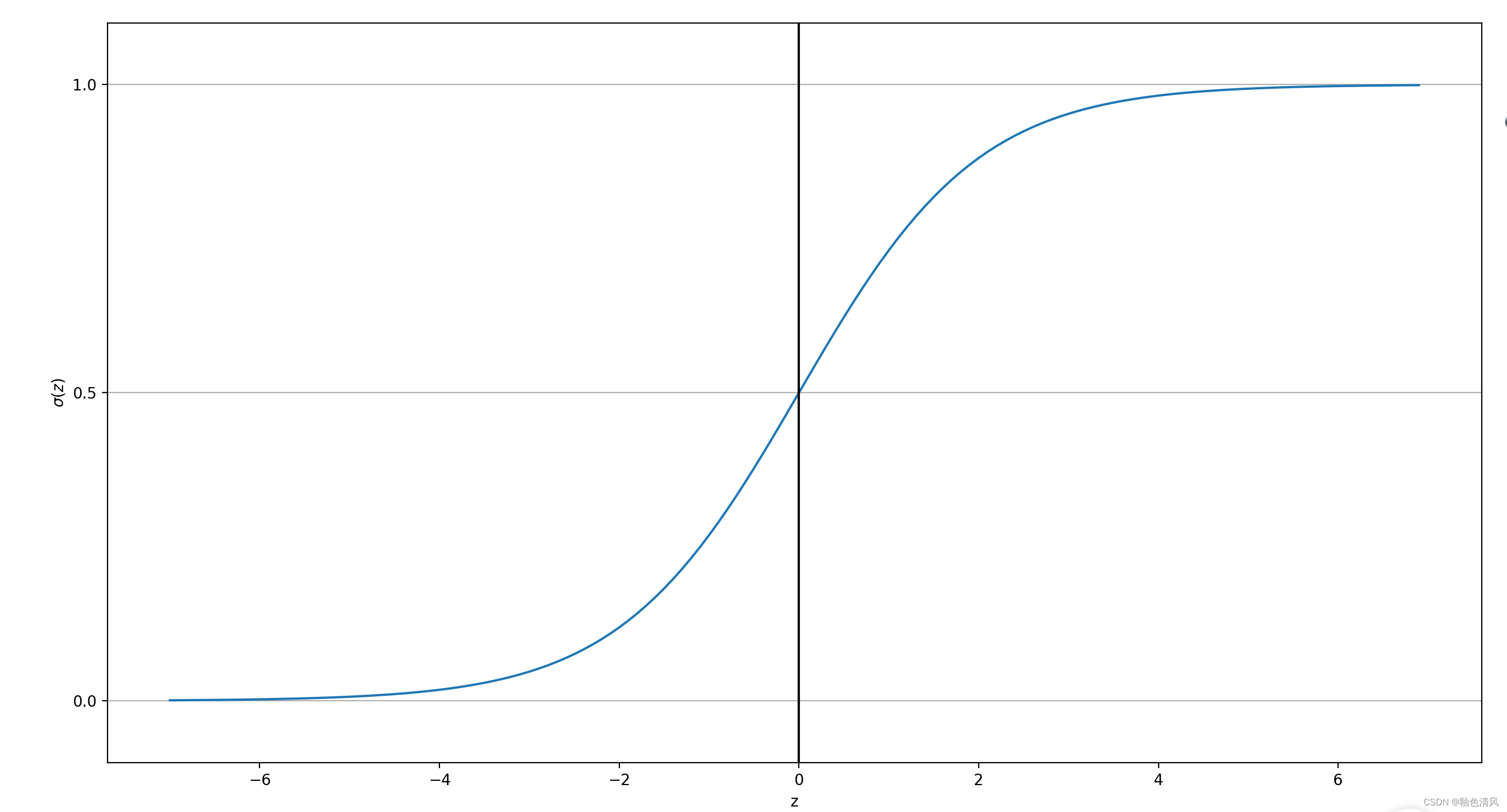
但輸入的$z$為0時，輸出p為0.5。當輸入的z趨近于$+\infty$時，輸出p接近于1。當輸入的趨近于$?\infty$時，輸出p接近于1。
而且當輸入的$z＞0$，那么p>0.5,可以判別是預測事件的發生。當$z＜0$時，可以認為是預測事件的不發生。即對應的二值輸出為:
$\hat{y}=\{\begin{array}{l}1如果\sigma (z)\ge 0.5\\ 0其他\end{array}$