FloodFill算法—

FloodFill算法就是用來尋找性質相同的連通快的算法，這篇博客都是用dfs來實現FloodFill算法

1.圖像渲染

題目鏈接：733. 圖像渲染 - 力扣（LeetCode）?

?題目解析：將和（sr,sc）相連的所有像素相同的點，將這些點的值都修改為目標值

算法講解：

利用深搜，遍歷所有與初始點相連的所有像素相同的點，然后將其修改成指定的像素值即可

代碼實現：

一個小細節：如果color==image[sr][sc]，此時就不用去遍歷image了，此時直接返回image即可，或者也可以創建一個check的boolean類型的數組，去標記已經訪問的位置

//第一種寫法
class Solution {int h,l,prev;int[] dx={0,0,1,-1};int[] dy={1,-1,0,0};public int[][] floodFill(int[][] image, int sr, int sc, int color) {h=image.length;l=image[0].length;prev=image[sr][sc];if(prev==color) return image;dfs(image,sr,sc,color);return image;}public void dfs(int[][] image,int i,int j,int color){image[i][j]=color;for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<h && y>=0 && y<l && image[x][y]==prev){dfs(image,x,y,color);}}}
}//第二種寫法
class Solution {int h,l,prev;int[] dx={0,0,1,-1};int[] dy={1,-1,0,0};boolean[][] check;public int[][] floodFill(int[][] image, int sr, int sc, int color) {h=image.length;l=image[0].length;check=new boolean[h][l];prev=image[sr][sc];dfs(image,sr,sc,color);return image;}public void dfs(int[][] image,int i,int j,int color){image[i][j]=color;for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<h && y>=0 && y<l && image[x][y]==prev && check[x][y]==false){check[x][y]=true;dfs(image,x,y,color);check[x][y]=false;}}}
}

2.島嶼數量?

題目鏈接：200. 島嶼數量 - 力扣（LeetCode）

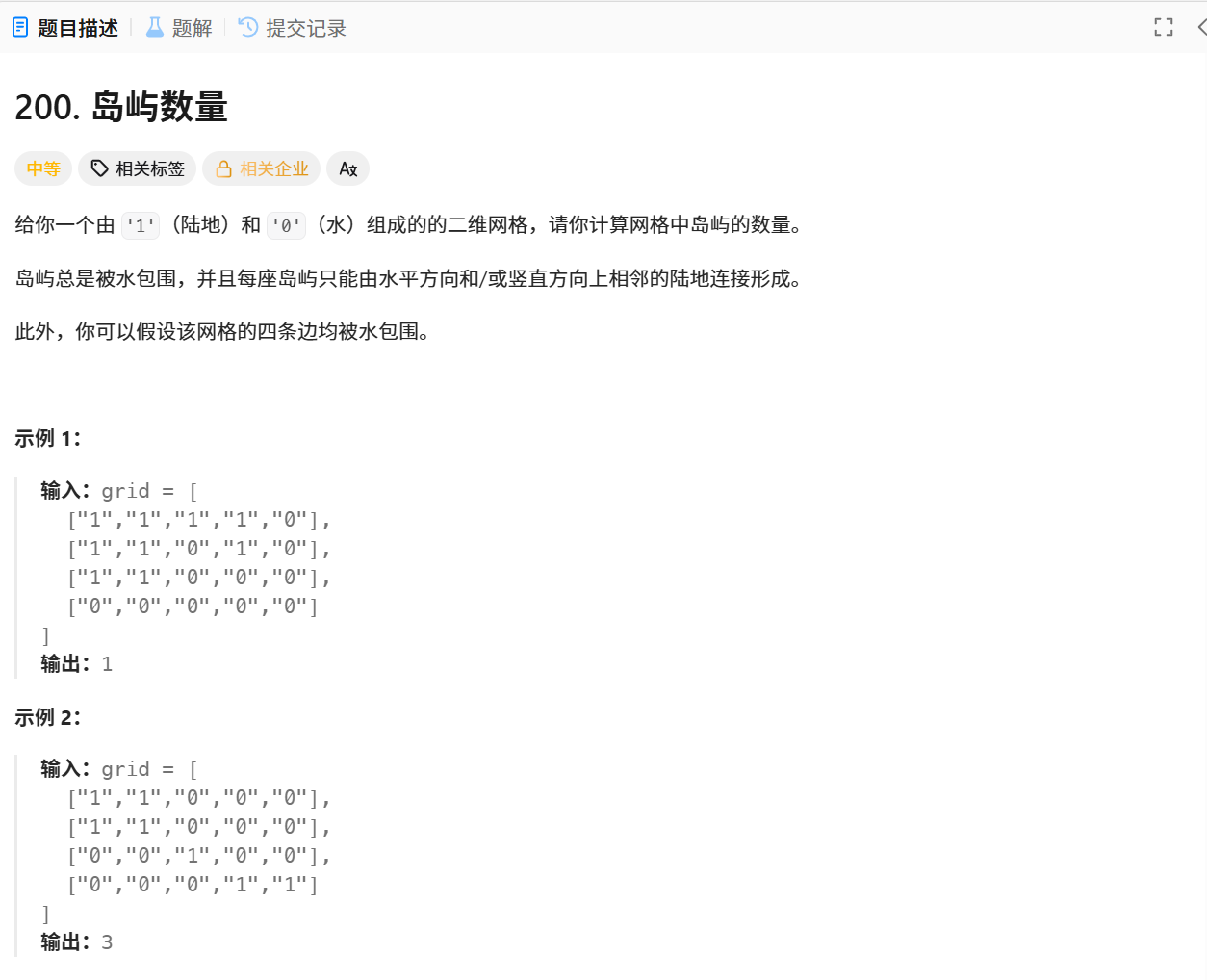?題目解析：計算島嶼的數量，也就是計算grid數組中數字為1的連通快的個數?

算法講解： FloodFill

首先要創建一個同等規模的check的boolean數組，先遍歷一遍grid數組，當遇到1時且該對應的check[i][j]==false，就通過dfs遞歸函數將這個位置的上下左右中為1的位置的對應到check數組中的值改為true即可

代碼實現：

class Solution {boolean[][] check;int h,l;int[] dx={0,0,-1,1};int[] dy={-1,1,0,0};public int numIslands(char[][] grid) {h=grid.length;l=grid[0].length;int ret=0;check=new boolean[h][l];for(int i=0;i<h;i++){for(int j=0;j<l;j++){if(grid[i][j]=='1'&&check[i][j]==false){ret++;dfs(grid,i,j);}}}return ret;}public void dfs(char[][] grid,int i,int j){check[i][j]=true;for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<h && y>=0 && y<l && check[x][y]==false && grid[x][y]=='1'){dfs(grid,x,y);}}}
}

?3.島嶼的最大面積

題目解析：返回最大島嶼的面積

算法講解：FloodFill

依舊是對grid數組做一遍深度優先遍歷，當遇到1時，就上下左右去尋找連通的1，且創建一個全局變量area去記錄每一次遞歸時找到的島嶼的面積

代碼實現：

代碼細節：每次遞歸之前要將area置為0，因為每一次遞歸都是去找新的島嶼，計算新的島嶼的面積之前，要將之前計算的島嶼的面積去掉，也就是將area置為0?

class Solution {boolean[][] vis;int h,l,area,ret;int[] dx={0,0,1,-1};int[] dy={1,-1,0,0};public int maxAreaOfIsland(int[][] grid) {h=grid.length;l=grid[0].length;vis=new boolean[h][l];for(int i=0;i<h;i++){for(int j=0;j<l;j++){if(grid[i][j]==1&&vis[i][j]==false){area=0;//小細節dfs(grid,i,j);ret=Math.max(ret,area);}}}return ret;}public void dfs(int[][] grid,int i,int j){area++;vis[i][j]=true;for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<h && y>=0 && y<l && grid[x][y]==1 && vis[x][y]==false){dfs(grid,x,y);}}}
}

4.被圍繞的區域

題目鏈接：130. 被圍繞的區域 - 力扣（LeetCode）?

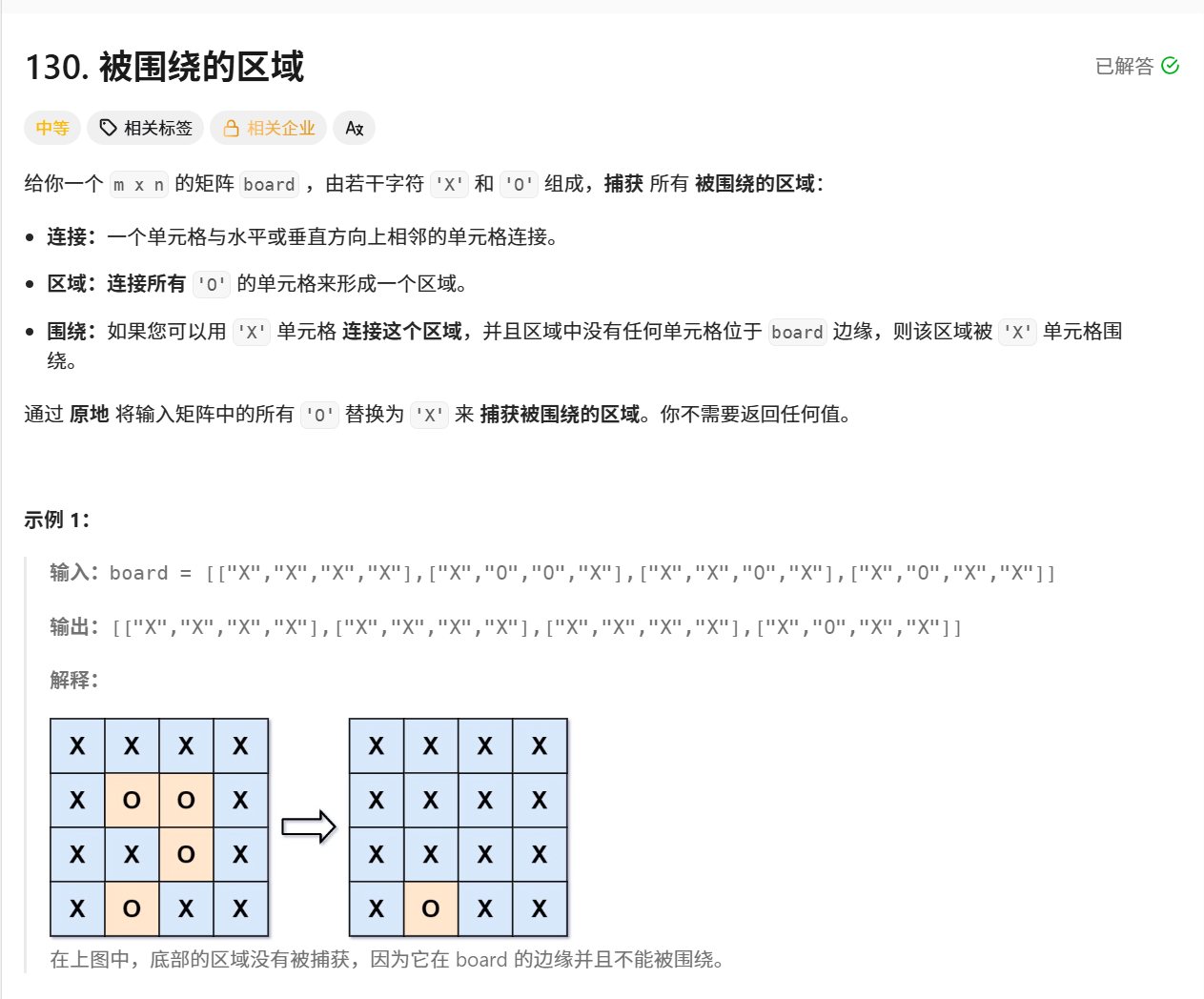?題目解析：將矩陣中的被X圍繞的連通O區域中的字母全部改為字母X

算法講解：FloodFill

這道題的難點就是在于處理位于邊界的連通O區域，如果我們直接對矩陣進行一遍深度遍歷，那馬就要寫兩個dfs函數，一個用來處理內部的O區域，另一個用來處理處于邊界的O區域，但是這樣寫是在是太復雜了

正難則反，，我們可以先去處理邊界的情況，先將位于邊界的連通O區域全部改為字符點，處理完邊界情況之后，在去遍歷矩陣，遇到字符點，則就將其還原成O，此時如果遇到O，那么此時的O區域肯定是合法的，此時直接將O改為X即可

代碼實現：

class Solution {int h,l;int[] dx={0,0,1,-1};int[] dy={1,-1,0,0};public void solve(char[][] board) {h=board.length;l=board[0].length;for(int j=0;j<l;j++){if(board[0][j]=='O') dfs(board,0,j);if(board[h-1][j]=='O') dfs(board,h-1,j);}for(int i=0;i<h;i++){if(board[i][0]=='O') dfs(board,i,0);if(board[i][l-1]=='O') dfs(board,i,l-1);}for(int i=0;i<h;i++){for(int j=0;j<l;j++){if(board[i][j]=='.') board[i][j]='O';else if(board[i][j]=='O') board[i][j]='X';}}}public void dfs(char[][] board,int i,int j){board[i][j]='.';for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<h && y>=0 && y<l && board[x][y]=='O'){dfs(board,x,y);}}}
}

5.太平洋大西洋流水問題?

題目鏈接：417. 太平洋大西洋水流問題 - 力扣（LeetCode）?

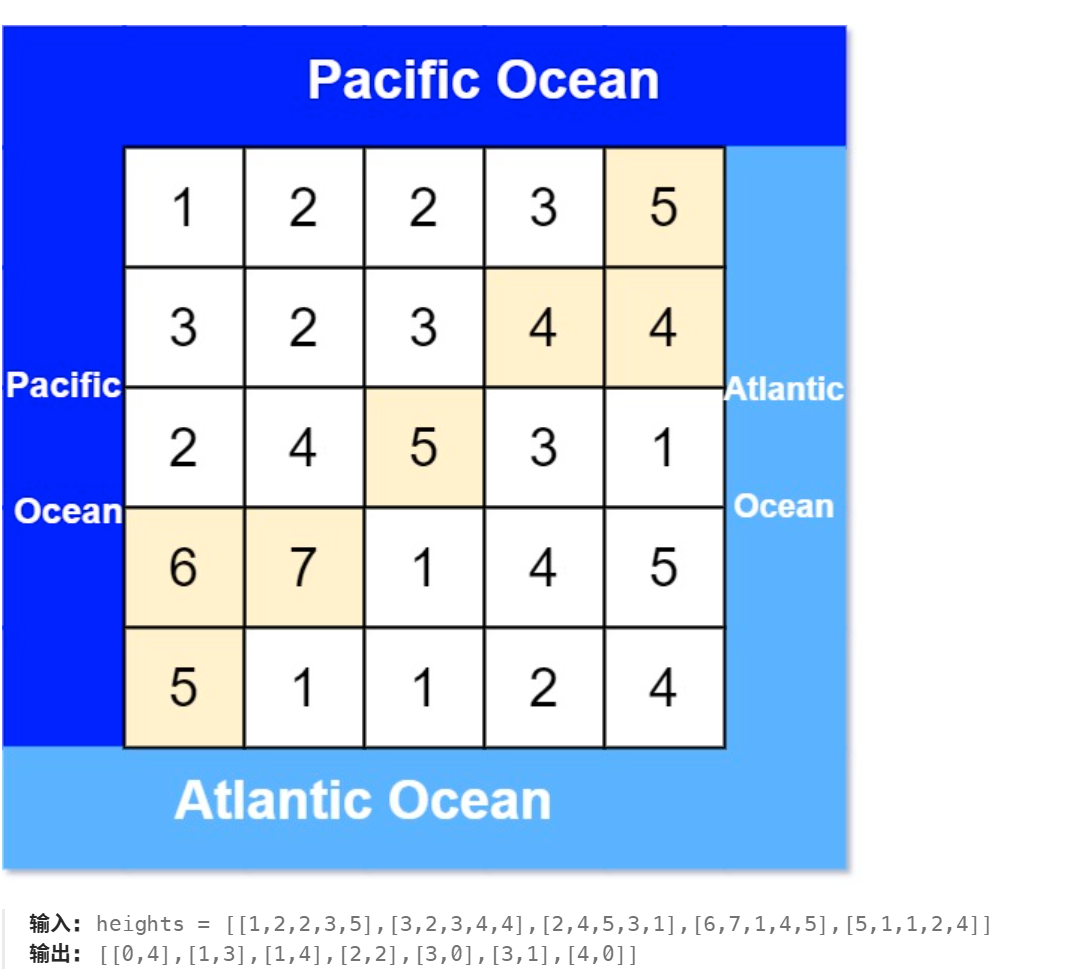
題目解析：找出矩陣中既能流入太平洋和大西洋的位置

解法一：直接暴搜

直接遍歷矩陣，直接對每一個位置進行一遍FloodFill，但是這樣會出現重復走大量的重復路徑，代碼可能會超時?

解法二：正難則反?

我們可以轉換一下思路，題目要求我們找出既能流入太平洋又能流入大西洋的位置，可以反過來思考，從太平洋或者大西洋能流入矩陣的哪一些位置，此時創建兩個同等規模的boolean類型的數組paci和atla，如果paci[i][j]或者atla[i][j]的值為true，那么就代表從太平洋或者大西洋的水能流入（i，j）位置，當paci[i][j]和atla[i][j]的值同時為true時，就代表太平洋和大西洋的水都能能流入（i，j）位置?

此時對分別對第一行和第一列，最后一行和最后一列，分別進行一遍FloodFill即可?

代碼實現：

class Solution { List<List<Integer>> ret;int h,l;int[] dx={0,0,1,-1};int[] dy={1,-1,0,0};public List<List<Integer>> pacificAtlantic(int[][] heights) {h=heights.length;l=heights[0].length;boolean[][] paci=new boolean[h][l];boolean[][] atla=new boolean[h][l];ret=new ArrayList<>();//處理太平洋//第一行for(int j=0;j<l;j++) dfs(heights,0,j,paci);//第一列for(int i=0;i<h;i++) dfs(heights,i,0,paci);//處理大西洋//最后一行for(int j=0;j<l;j++) dfs(heights,h-1,j,atla);//最后一列for(int i=0;i<h;i++) dfs(heights,i,l-1,atla);for(int i=0;i<h;i++){for(int j=0;j<l;j++){if(paci[i][j]==true&&atla[i][j]==true){List<Integer> tmp=new ArrayList<>();tmp.add(i);tmp.add(j);ret.add(tmp);}}}return ret;}public void dfs(int[][] heights,int i,int j,boolean[][] ocean){ocean[i][j]=true;for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<h && y>=0 && y<l && heights[x][y]>=heights[i][j] && ocean[x][y]==false){dfs(heights,x,y,ocean);}}}
}

6.掃雷游戲?

題目鏈接：529. 掃雷游戲 - 力扣（LeetCode）?

題目解析：就是掃雷游戲的規則，點擊一個為挖出的方塊，則與這個空格相連的空格也會被展開，如果某一個空格的相鄰有地雷的花，就不展開與這個空格相鄰的空格，只需要將這個空格的值改為地雷的數量即可

算法講解：FloodFill?

這道題就是對棋盤從點擊的位置進行一遍深度遍歷即可，如果遇到為挖出的空格，則將其翻轉即可，但是如果未挖出的空格相鄰位置有地雷，將這個空格的值改為地雷的數量

則此時dfs函數就是用來翻轉空格的，但是翻轉的情況有兩種，如果空格的相鄰位置沒有地雷，將M改為B即可，如果空格的相鄰位置有地雷，要將M給為地雷的數量，所以此時在遞歸之前，要對地雷的數量進行一個判斷

代碼實現：

class Solution {int h,l;int[] dx={0,0,-1,1,-1,-1,1,1};int[] dy={-1,1,0,0,-1,1,-1,1};public char[][] updateBoard(char[][] board, int[] click) {h=board.length;l=board[0].length;int x=click[0];int y=click[1];if(board[x][y]=='M'){board[x][y]='X';return board;}dfs(board,x,y);return board;}public void dfs(char[][] board,int i,int j){//判斷地雷的數量int count=0;for(int k=0;k<8;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<h && y>=0 && y<l && board[x][y]=='M'){count++;}}if(count==0){board[i][j]='B';for(int k=0;k<8;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<h && y>=0 && y<l && board[x][y]=='E'){dfs(board,x,y);}}}else{board[i][j]=(char)('0'+count);}}
}

7. 衣櫥整理

題目鏈接：LCR 130. 衣櫥整理 - 力扣（LeetCode）?

題目描述：如上圖

算法講解：FloodFill

依舊是對m行n列的放個做一遍深度優先遍歷即可

代碼實現：

class Solution {int ret;int h,l;boolean[][] vis;int[] dx={0,0,-1,1};int[] dy={-1,1,0,0};public int wardrobeFinishing(int m, int n, int t) {h=m;l=n;vis=new boolean[h][l];dfs(0,0,t);return ret;}public void dfs(int i,int j,int t){vis[i][j]=true;ret++;for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];int tmp=(x/10)+(x%10)+(y/10)+(y%10);if(x>=0 && x<h && y>=0 && y<l && tmp<=t && vis[x][y]==false){dfs(x,y,t);}}}
}