Swin-Transformer從淺入深詳解

第一部分：出現背景

在 Swin Transformer 出現之前，計算機視覺（Computer Vision, CV）領域主要由 CNN (卷積神經網絡) 主導。后來，NLP（自然語言處理）領域的 Transformer 模型被引入 CV，誕生了 ViT (Vision Transformer)。

ViT 做了一件事：它將一張圖片分割成多個“圖塊”（Patches），把這些圖塊當作句子里的“單詞”，然后用標準 Transformer 模型來處理，取得了驚人的效果。

但是，ViT 存在兩個核心問題：

1.計算復雜度過高：

標準的 Transformer 需要計算每個圖塊（Patch）與其他所有圖塊之間的“注意力”，這是一種全局（Global）注意力機制。如果一張圖片有 N 個圖塊，計算復雜度就是 O(N*N)。當圖片分辨率增大時，N 會急劇增加，導致計算量和顯存消耗變得難以承受。

2.缺乏層次化結構：

CNN 的一大優勢是它能通過逐層堆疊（卷積、池化），構建出從低級（邊緣、紋理）到高級（物體部件、整體）的層次化特征。這種金字塔結構對于物體檢測、語義分割等需要多尺度信息的任務至關重要。而 ViT 從始至終都保持著同樣大小的圖塊序列，缺乏這種多尺度的能力。

Swin Transformer 的誕生，就是為了解決 ViT 的這兩個核心痛點。它的目標是：打造一個既有 Transformer 的強大建模能力，又有 CNN 的高效性和層次化結構優點的通用視覺骨干網絡

注：部分圖示出自論文原文與小綠豆老師的博客

第二部分：網絡整體架構

在探討Swin Transformer 的核心設計之前，我們先看一下他和Vision Transformer（VIT）的不同，這里引用小綠豆老師的博文和圖來進行對比講解：

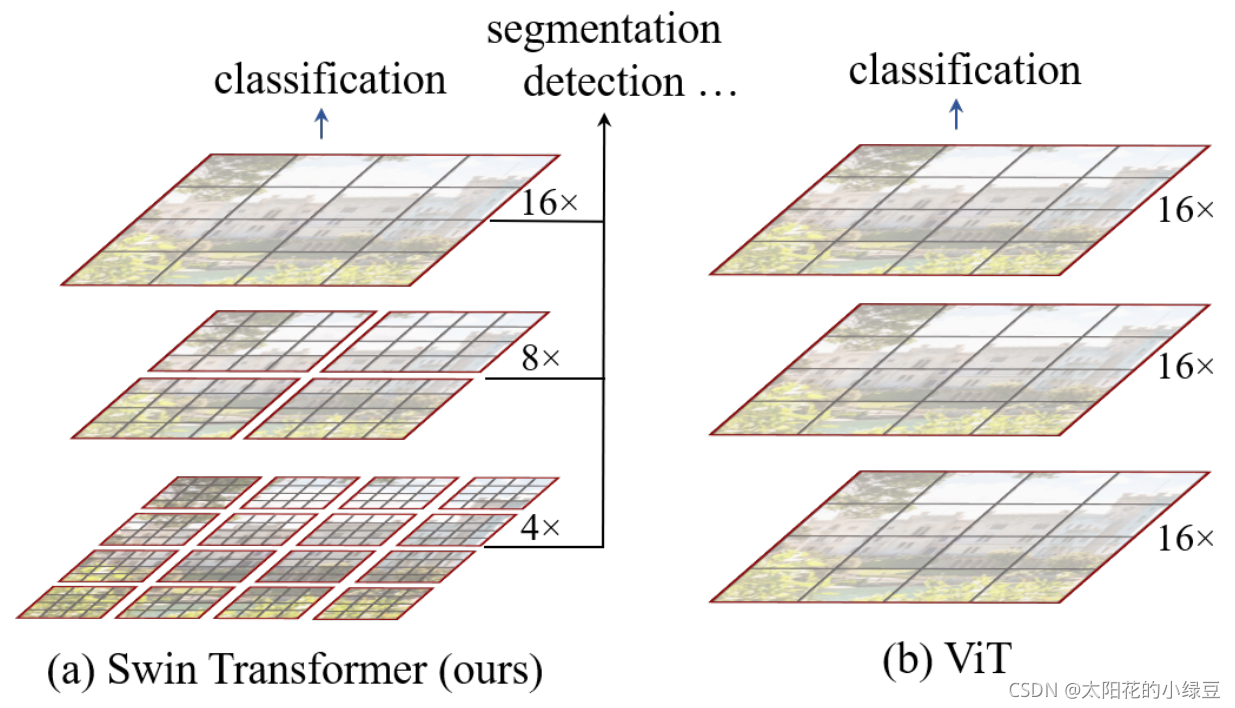
通過對比我們可以看出主要的不同：

Swin Transformer和CNN很類似，分層次構建的特征圖，這樣有助于各種任務的建立，而VIT主要還是比較單一的16倍下采樣。

原論文中給出的關于Swin Transformer（Swin-T）網絡的架構圖：

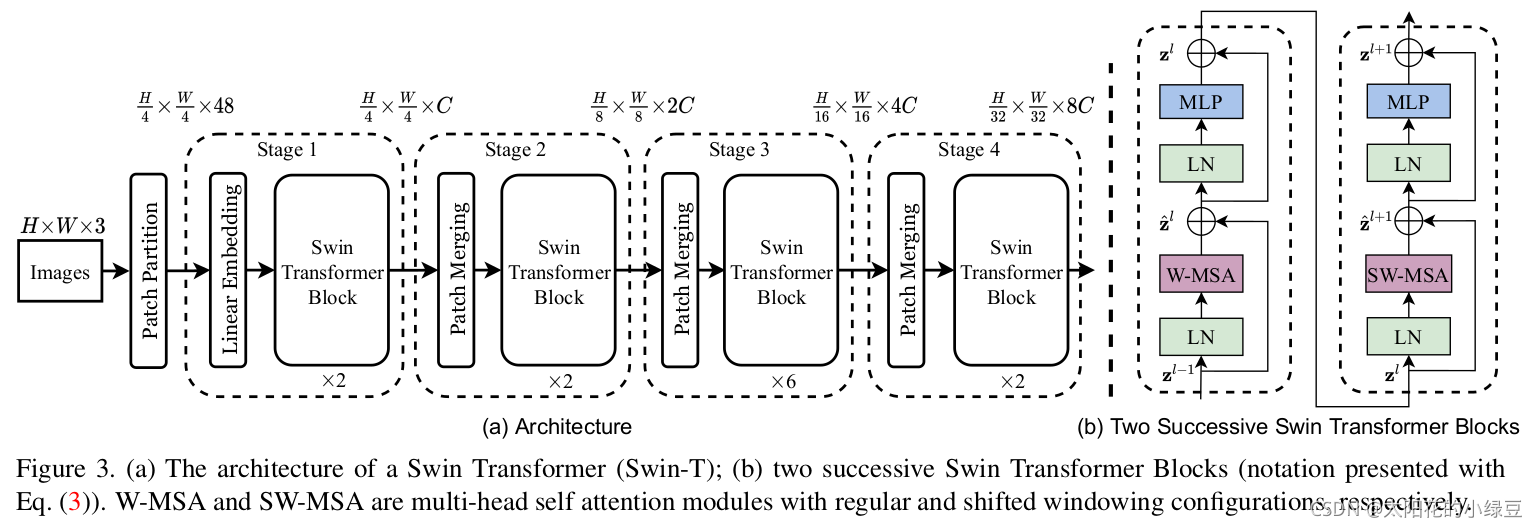
大家先簡單看一下，在后面我會詳細展開講解各個模塊的作用，Swin Transformer 的架構非常有 CNN 的風范，呈現出清晰的層次化結構。

整個網絡主要分為 4 個階段（Stage）：

Stage 1: Patch Partition & Linear Embedding

1.輸入：一張 H x W x 3 的 RGB 圖像。

2.操作：

Patch Partition: 像 ViT 一樣切塊，但 Swin 的初始塊非常小，比如 4 x 4 像素。這樣每個圖塊就是一個 4 * 4 * 3 = 48 維的向量。

Linear Embedding: 通過一個線性層，將每個圖塊的維度映射到一個指定的維度 C（例如 96）。

3.輸出：一個大小為 (H/4) x (W/4)，通道數為 C 的特征圖。

Stage 2: Swin Transformer Blocks

1.輸入：Stage 1 的輸出。

2.操作：

串聯多個 Swin Transformer Block。這些 Block 成對出現：

第一個 Block 使用 W-MSA，第二個 Block 使用 SW-MSA...如此交替，注意：一定是成對的偶數出現！！！

3.輸出：特征圖大小不變，仍為 (H/4) x (W/4) x C。

Stage 3: Patch Merging & More Blocks

1.輸入：Stage 2 的輸出。

2.操作：Patch Merging (核心步驟):

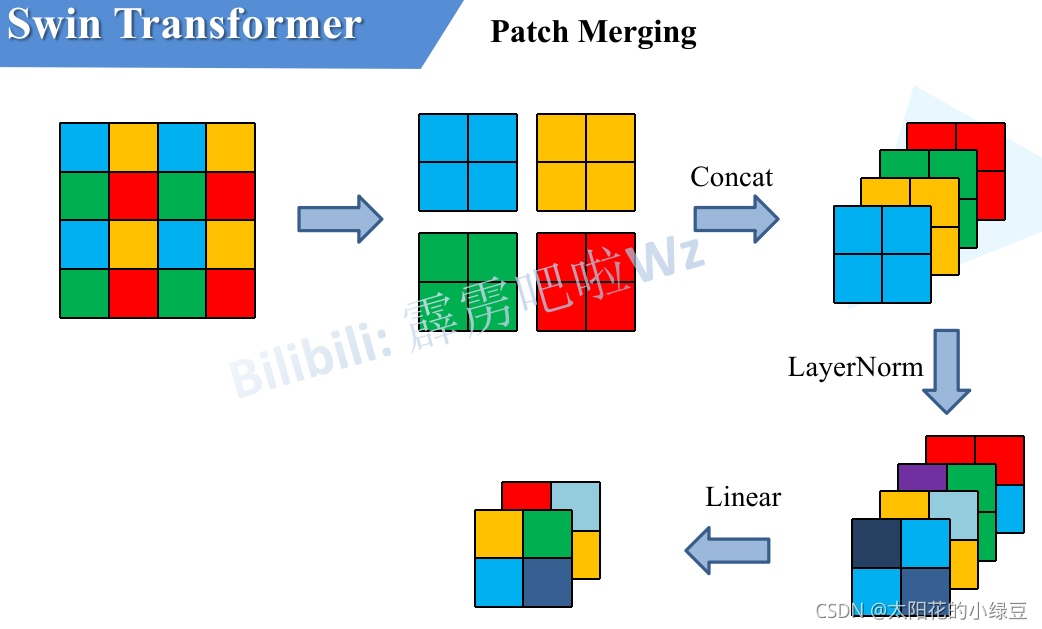
這是一個下采樣層，作用類似于 CNN 中的池化層。它將特征圖中每 2 x 2 相鄰的四個圖塊拼接（Concatenate）在一起，這樣通道數變為 4C，再通過一個線性層將通道數降為 2C。

我們可以把它看做，一個3x3的正方形網格，網格內像素值為1，對特征圖進行采樣，每次采樣只保留正方形四個角的像素，這樣我們就可以采樣到4個新的特征圖，隨后將這四個新的特征圖拼接到一起，這就是我們的Patch Merging

效果：特征圖分辨率減半 ((H/8) x (W/8))，通道數翻倍 (2C)。這完美復刻了 CNN 的金字塔結構

Swin Transformer Blocks: 再次串聯多個成對的 (W-MSA, SW-MSA) Block，對新的特征圖進行處理。

3.輸出：(H/8) x (W/8) x 2C 的特征圖。

Stage 4 & Stage 5: 重復操作

繼續重復 Patch Merging + Swin Transformer Blocks 的組合。

Stage 4 輸出: (H/16) x (W/16) x 4C 的特征圖。

Stage 5 輸出: (H/32) x (W/32) x 8C 的特征圖

最后，根據具體任務（如圖像分類），在最后一層特征圖后接上全局平均池化層和全連接層進行預測。

第二部分：核心模塊講解

模塊一：窗口化多頭自注意力 (W-MSA)

核心思想：在現實世界中，一個像素點和它周圍的像素點的關系，遠比和圖像另一端的像素點的關系要密切。這是視覺最基本的物理常識。

既然全局注意力的計算量太大，一個自然的想法就是：我們能不能只在一個局部范圍內計算注意力？左邊為VIT的特征圖，需要每個像素去乘以剩下的像素去計算注意力，就是16x16，而右邊的SWIN，僅僅在4個窗口分別計算注意力，就成了4x4x4，一下就減少了這么多，更別提在高分辨率下1920x1080的圖像了，那肯定計算資源減少的更多！

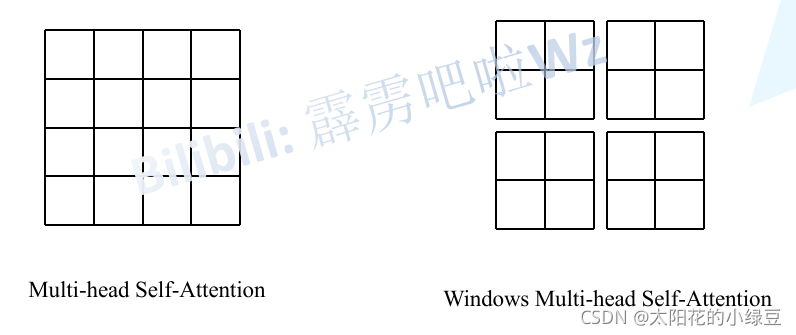
Swin Transformer 正是這么做的。它沒有在整張特征圖上計算注意力，而是：

1.劃分窗口 (Window Partitioning)：將特征圖（Feature Map）劃分為多個不重疊的窗口（比如每個窗口大小為 M x M 個圖塊）。

2.窗口內注意力 (Attention within Window)：在每個窗口內部獨立地進行自注意力計算。

這樣做的好處立竿見影：

沒有窗口的ViT 的全局注意力復雜度：O((h * w)2)

SWIN:假設特征圖有 h x w 個圖塊，窗口大小為 M x M。

Swin 的窗口注意力復雜度：O(M2 * h * w)

當 M 是一個固定的小常數（如 7）時，計算復雜度就從關于圖塊數量的二次方關系，變成了線性關系！這極大地降低了計算量，使得處理高分辨率圖像成為可能。

但是，新問題來了：每個窗口都像一個信息孤島，窗口之間無法進行信息交流。這樣模型就無法學習到跨越窗口邊界的全局特征。怎么辦？這就引出了第二個核心模塊。

模塊二：“移位窗口”實現跨窗口連接 (Shifted Window Self-Attention, SW-MSA)

為了打破窗口間的壁壘，Swin Transformer 設計了一個絕妙的機制：移位窗口。

它的操作非常天才！：

通過前文的網絡整體架構設計，我們知道W-MSA和SW-MSA一般成對出現，在連續的兩個 Transformer Block 中，它會采用兩種不同的窗口劃分方式：

即：

1.在一個 Transformer Block 中，使用常規的 W-MSA。

2.在下一個連續的 Transformer Block 中，將窗口的劃分方式進行移位（Shift）。具體來說，將窗口向右和向下移動半個窗口的距離，即 (M/2 向下取整, M/2 向下取整) 的距離。這里的M是4，于是我們向下向右移兩個像素，這個簡單的“移位”操作，帶來了神奇的效果。在第 L 層還分屬不同窗口、無法直接對話的圖塊，在第 L+1 層因為窗口的移動，被“劃分”到了同一個新窗口中，從而可以進行信息交互了。

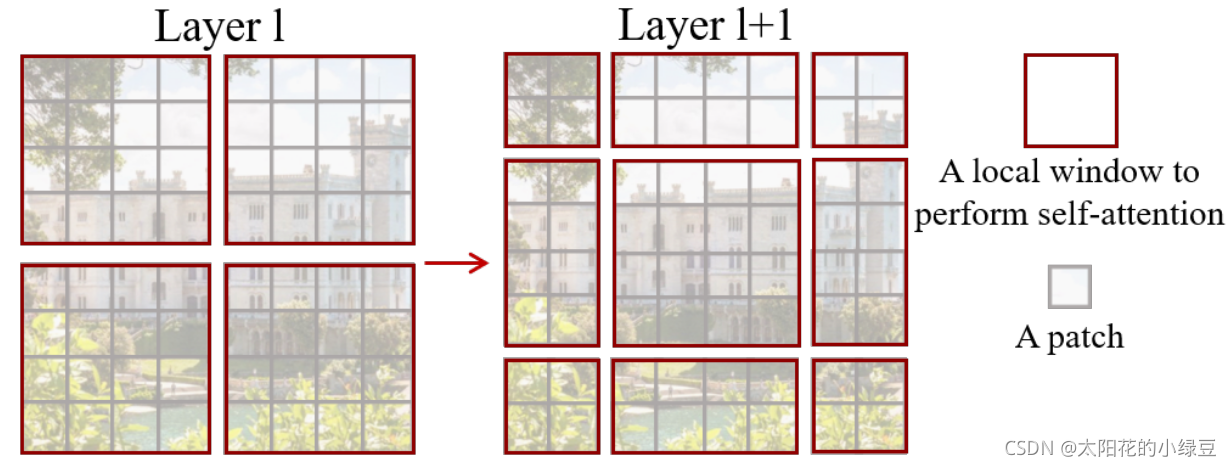
但是！！！如果真的按照移位后的樣子去老老實實計算，會產生更多、大小不一的窗口，從而增加計算量并且難以并行處理。

但 Swin Transformer 的作者用了一個極其聰明的“障眼法”來解決這個問題，這個技巧叫做 循環移位 (Cyclic Shift) + 注意力掩碼 (Masking)。它實現了“跨窗口交流”的效果，卻沒有增加一丁點計算量。所以我一直認為這個作者真的是天才，Swin的架構設計簡直像一種藝術。接下來我來講解一下這個技巧。

第一步：不創建新窗口，而是“滾動”特征圖 它并不真的去切分出那些邊邊角角的小窗口。相反，它把整張特征圖向上、向左進行“循環移位”（可以想象成把最左邊的像素塊移動到最右邊，最上邊的移動到最下邊）。說白了，就是把通過移動特征圖，把圖里不同區域劃分到格子里去。

效果：經過這個“滾動”操作后，原來那些因為移位而產生的零碎小窗口，被神奇地重新拼湊在了一起。最終，我們得到的仍然是和常規 W-MSA 數量相同、大小也完全相同的窗口。這樣計算量就保持不變了！

第二步：解決“亂點鴛鴦譜”的問題 但是，這個“滾動”操作帶來一個新問題：一些原本在圖像中天各一方的區域被硬湊到了一個窗口里，比如最上面的一排像素，滾動到了最下面，這樣他和之前最下面的像素沒啥聯系啊，計算注意力沒必要啊。

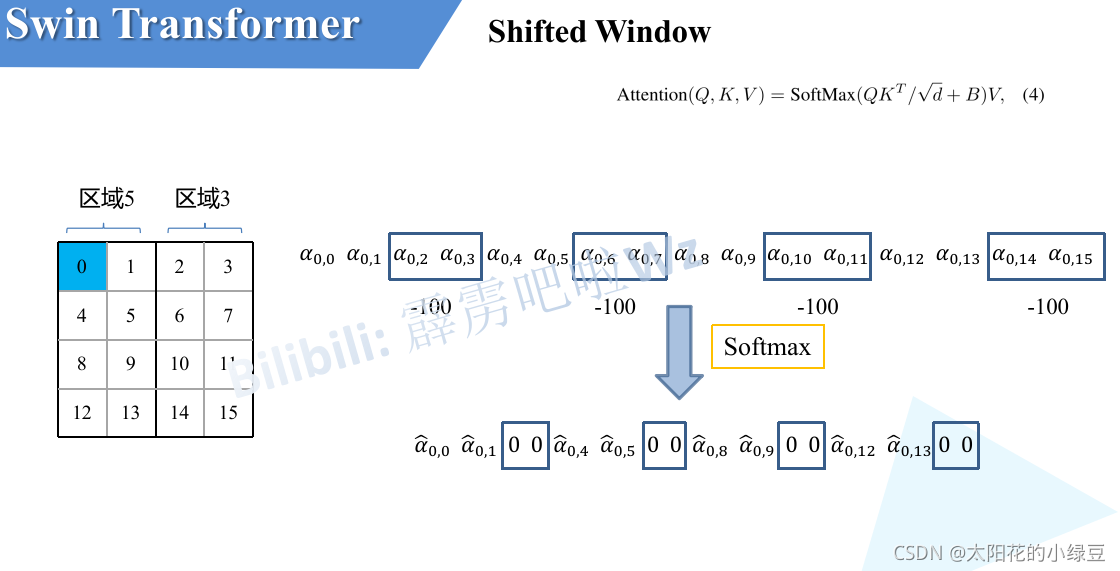
第三步：使用“注意力掩碼” 為了解決這個問題，模型在計算注意力之前，會使用一個“掩碼 (Mask)”。這個掩碼會告訴模型：最下面一排像素和倒數第二排像素的圖塊是硬湊過來的，你們之間不準計算注意力?在計算時，它會給這些不該交流的圖塊組合一個極大的負值（比如 -100），這樣經過 Softmax 之后，它們之間的注意力權重就幾乎為 0 了。

比如，像素0屬于區域5，當像素0計算注意力時，就把區域3內所有像素添加一個-100，這樣就不會計算硬湊的模塊注意力了

第四步：計算完畢，物歸原主 在帶有掩碼的注意力計算完成之后，再把特征圖“反向滾動”回去，恢復到它本來的樣子。

通過?“循環移位 -> 帶掩碼計算 -> 逆向移位”?這一套流程，Swin Transformer 巧妙地在邏輯上實現了跨窗口的信息流動，但在實際計算時，處理的窗口數量和大小從未改變。

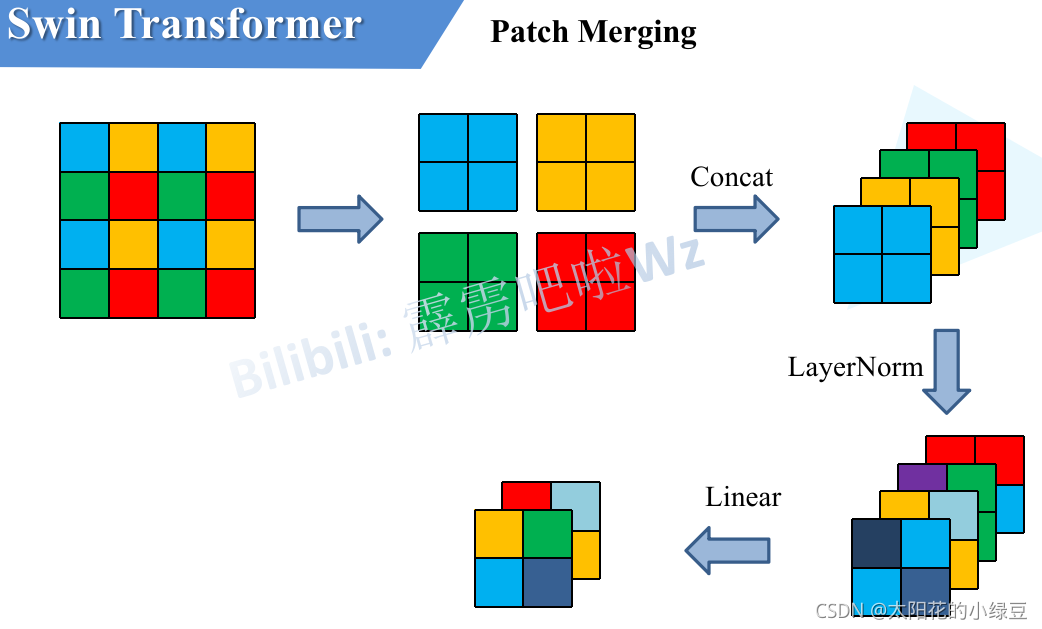
模塊三：Patch Merging (圖塊合并)

一、設計的核心動機：為何不直接用 CNN 的池化 (Pooling)？

在深入了解 Patch Merging 的“如何做”之前，我們必須先明白“為什么這么做”。CNN 中最常見的降采樣方法是最大池化 (Max Pooling) 或平均池化 (Average Pooling)。

池化的問題：池化操作非常粗暴。比如最大池化，在一個 2x2 的區域里，它只保留最大的那個值，其他三個值的信息就被完全丟棄了。這是一種不可逆的信息損失。雖然它在早期 CNN 中很有效，但對于需要精細建模的 Transformer 架構來說，這種信息損失是不可接受的。

Patch Merging 的設計：先保留全部，再學習如何提煉。 它認為，2x2 區域內的 4 個圖塊（像素）都包含了有用的信息，我們不應該武斷地扔掉任何一個。正確的做法是，把這 4 份信息完整地“打包”在一起，然后通過一個可學習的網絡層（線性層），讓模型自己去決定如何從這包信息中提煉出最重要的部分。

我們可以把它看做，一個3x3的正方形網格，網格內像素值為1，對特征圖進行采樣，每次采樣只保留正方形四個角的像素，這樣我們就可以采樣到4個新的特征圖，隨后將這四個新的特征圖拼接到一起，再通過一個線性層將通道數降為 2C。

因此，Patch Merging 的本質是一種無損、可學習的降采樣（下采樣）方法。