In time series analysis, the presence of dirty and messy data can alter our reasonings and conclusions. This is true, especially in this domain, because the temporal dependency plays a crucial role when dealing with temporal sequences.

在時間序列分析中，臟數據和雜亂數據的存在會改變我們的推理和結論。 這是正確的，尤其是在此領域，因為在處理時間序列時，時間依賴性起著至關重要的作用。

Noise or outliers must be handled with care following ad-hoc solutions. In this situation, the tsmoothie package can help us save a lot of time in preparing time series for our analysis. Tsmoothie is a python library for time series smoothing and outlier detection that can handle multiple series in a vectorized way. It’s useful because it can provide the preprocess steps we needed, like denoising or outlier removal, preserving the temporal pattern present in our raw data.

按照臨時解決方案，必須小心處理噪聲或異常值。 在這種情況下， tsmoothie軟件包可以幫助我們節省大量時間來準備用于分析的時間序列。 Tsmoothie是用于時間序列平滑和離群值檢測的python庫，可以以矢量化方式處理多個序列。 這很有用，因為它可以提供我們所需的預處理步驟，例如去噪或離群值去除，保留原始數據中存在的時間模式。

In this post, we use these trinks to improve a clustering task. More precisely, we try to identify some changes in financial data carrying out an unsupervised approach. In the end, we will expect to point out clear patterns in the closing prices that can be used to inspect the hidden behavior of the market.

在本文中，我們將使用這些工具來改善聚類任務。 更準確地說，我們嘗試在無監督的情況下識別財務數據中的某些變化。 最后，我們期望指出收盤價的清晰模式，可用于檢查市場的隱藏行為。

數據 (THE DATA)

As introduced before, we operate with financial time series. There are a lot of tools or premade datasets that provide and store financial data. For our aims, we use a dataset collected from Kaggle. The Stock data 2000–2018 is a cleaned collection of stock prices from 2000 to 2018 of around 39 different stocks. It reports volumes, open, high, low, and close prices daily. We focus on the close prices.

如前所述，我們使用財務時間序列進行操作。 有很多提供或存儲財務數據的工具或預制數據集。 為了我們的目標，我們使用從Kaggle收集的數據集。 2000-2018年的股票數據是從2000年到2018年大約39種不同股票的干凈價格集合。 它每日報告交易量，開盤價，最高價，最低價和收盤價。 我們關注收盤價。

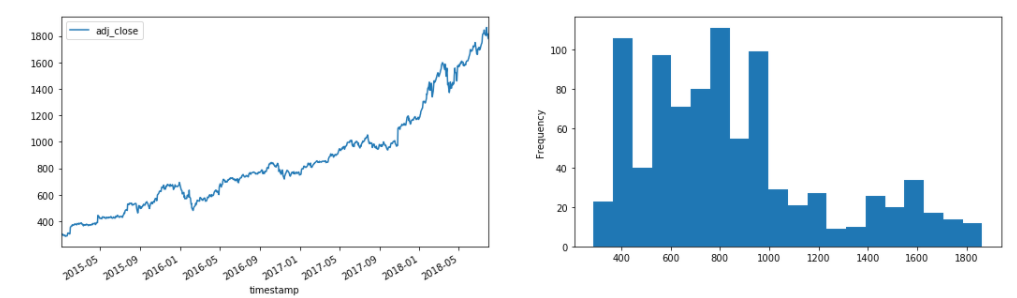
For a demonstrative purpose, we consider the Amazon stock price but the same findings appear also in other stock signals.

出于說明目的，我們考慮了亞馬遜股票的價格，但在其他股票信號中也出現了相同的發現。

時間序列平滑 (Time Series Smoothing)

The first step in our workflow consists of time series preprocessing. Our strategy is very intuitive and effective. Given a time series of closing prices, we split it into small sliding pieces. Each piece is then smooth in order to remove outliers. The smoothing process is essential to reduce the noise present in our series and point out the true patterns that may present over time.

我們工作流程的第一步包括時間序列預處理。 我們的策略非常直觀有效。 給定一個時間序列的收盤價，我們將其分為幾個小塊。 然后，每片都是光滑的，以去除異常值。 平滑過程對于減少我們系列中存在的噪聲并指出隨著時間推移可能出現的真實圖案至關重要。

Tsmoothie provides different smoothing techniques for our purpose. It also has the built-in utility to operate a sliding smoothing approach. The raw time series is partitioned into equal windowed pieces which are then smoothed independently. We select the Locally Weighted Scatterplot Smooth (LOWESS) as the smoothing procedure.

Tsmoothie為我們的目的提供了不同的平滑技術。 它還具有內置實用程序，可操作滑動平滑方法。 原始時間序列被分成相等的窗口部分，然后分別進行平滑。 我們選擇局部加權散點圖平滑( LOWESS )作為平滑過程。

LOWESS is a powerful non-parametric technique for fitting a smoothed line for given data either through univariate or multivariate smoothing. It implements a regression on a collection of points in a moving range, and weighted according to distance, around abscissa values in order to calculate ordinal values. The selection of the smoothing parameter (alpha) is often entirely based on a “repeated trial” basis. There is no specific technique for the selection of its exact value. The selection of a particular value may lead to “over-smoothing” or “under-smoothing”.

LOWESS是一種強大的非參數技術，可通過單變量或多變量平滑擬合給定數據的平滑線。 它對移動范圍內的點集合進行回歸，并根據距離在橫坐標值附近加權，以便計算序數值。 平滑參數( alpha )的選擇通常完全基于“重復試驗”。 沒有用于選擇其確切值的特定技術。 選擇特定值可能會導致“過度平滑”或“欠平滑”。

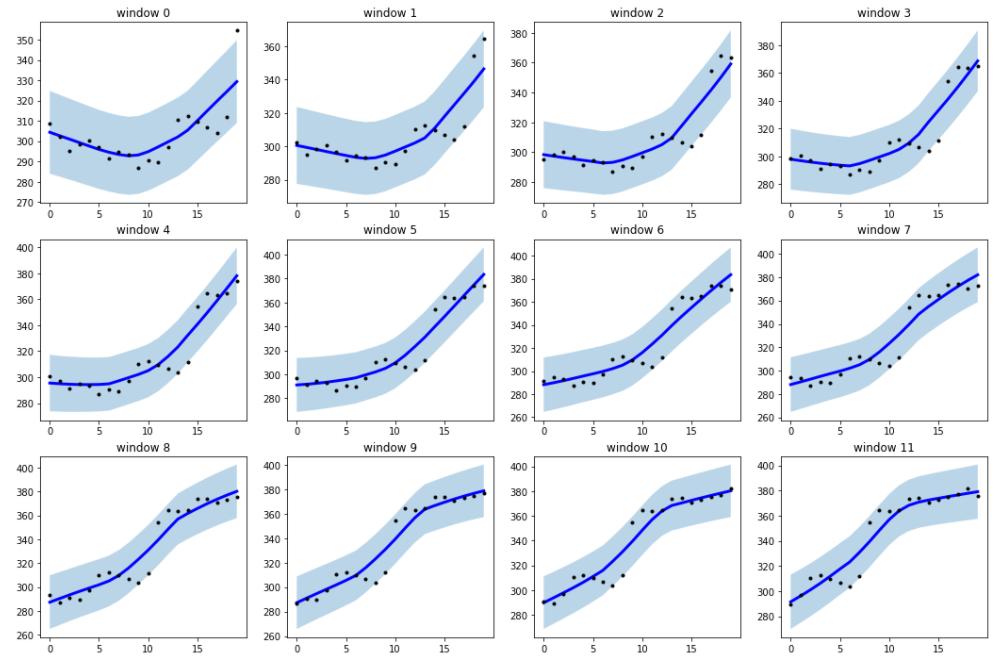
Below the result of applying the mentioned procedure with sliding windows of length 20 (days) and alpha equal to 0.6. In other words, we are computing a LOWESS for every generated window.

下面是使用長度為20(天)且alpha等于0.6的滑動窗口應用上述過程的結果。 換句話說，我們正在為每個生成的窗口計算一個LOWESS。

時間序列聚類 (Time Series Clustering)

The second step involves the usage of a clustering algorithm to identify the behaviors in our time series. The creation of equal length windows is aimed to solve this task easily.

第二步涉及使用聚類算法來識別時間序列中的行為。 等長窗口的創建旨在輕松解決此任務。

Generally speaking, clustering different time series into similar groups is challenging because each data point follows a temporal structure that we must respect in order to obtain satisfactory results. The distance measures used in standard clustering algorithms, such as Euclidean distance, are often not appropriate to time series. A stronger approach is to replace the default distance measure with a metric for comparing time series, such as Dynamic Time Warping.

一般而言，將不同的時間序列聚類為相似的組具有挑戰性，因為每個數據點都遵循一個時間結構，為了獲得令人滿意的結果，我們必須遵循該時間結構。 標準聚類算法中使用的距離度量(例如歐幾里得距離)通常不適用于時間序列。 一種更強大的方法是用一種用于比較時間序列的度量標準來代替默認距離度量，例如Dynamic Time Warping 。

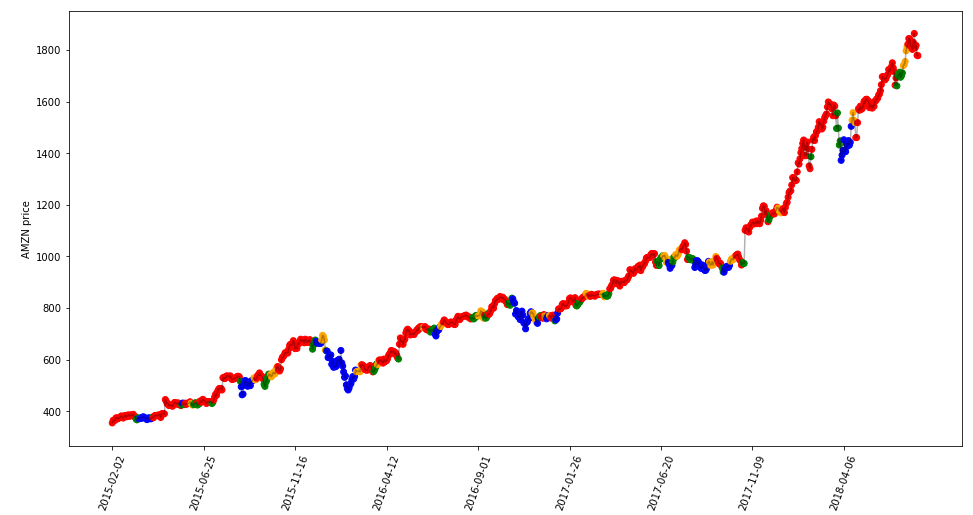
The search of 4 clusters with K-means and Dynamic Time Warping metric produces the following results:

使用K均值和動態時間規整度量標準對4個聚類進行搜索會產生以下結果：

As we can see, it’s evident the creation of 4 different clusters that represent 4 different market movements: an increasing trend (cluster 0), a decreasing trend (cluster 1), a downward turning point (cluster 2), an upward turning point (cluster 3). We can do the same with our raw time windows without computing the smoothing and make a comparison.

如我們所見，很明顯，創建了代表4個不同市場運動的4個不同的集群：上升趨勢( 集群0 )，下降趨勢( 集群1 )，下降拐點( 集群2 )，上升拐點( 集群 ) 組3 )。 我們可以對原始時間窗口執行相同操作，而無需計算平滑度并進行比較。

Now the difference between the 4 groups is not so marked. It’s more difficult to provide an interpretation of the generated clusters. The ability to generate meaningfully groups from a clustering algorithm is the more important prerequisite of any unsupervised approach. If we can’t attribute an explanation, the results can’t be utilized to make a decision. In this sense, the adoption of a smoothing preprocess can help the analysis.

現在，這四個組之間的差異不再那么明顯。 提供對生成的集群的解釋更加困難。 從聚類算法生成有意義的組的能力是任何無監督方法的重要前提。 如果我們無法解釋原因，那么結果將無法用于做出決定。 從這個意義上講，采用平滑預處理可以幫助分析。

摘要 (SUMMARY)

In the financial domain, the concept of volatility is fundamental to take decisions. It measures the uncertainty, i.e. the risk, present in the market. Here we went deeper extending our idea of market regimes in the short term. We identified four clear market conditions, smoothing our time series blocks to better understand the real dynamic of the data. In this post, we took advantage of the time series smoothing in a financial clustering application but this approach is valid and useful in some other contests involving time series analysis.

在金融領域，波動性概念是做出決策的基礎。 它測量市場中存在的不確定性，即風險。 在這里，我們在短期內更深入地擴展了市場體制的概念。 我們確定了四個明確的市場條件，從而平滑了時間序列塊，以更好地了解數據的真實動態。 在本文中，我們利用了金融聚類應用程序中的時間序列平滑功能，但是這種方法在涉及時間序列分析的其他一些競賽中是有效且有用的。

CHECK MY GITHUB REPO

檢查我的GITHUB回購

Keep in touch: Linkedin

保持聯系： Linkedin