上采樣與下采樣
概念:
上采樣:
放大圖像(或稱為上采樣(upsampling)或圖像插值(interpolating))的主要目的 是放大原圖像,從而可以顯示在更高分辨率的顯示設備上。
下采樣:
縮小圖像(或稱為下采樣(subsampled)或降采樣(downsampled))的主要目的 有兩個:
1、使得圖像符合顯示區域的大小;2、生成對應圖像的縮略圖。
實現方法:
上采樣原理:內插值
下采樣原理:(M/s) * (N/s)(同比例縮小)
插值方法:
一:最鄰近插值The nearest interpolation
設i+u, j+v(i, j為正整數, u, v為大于零小于1的小數,下同)為待求象素坐標,則待求象素灰 度的值 f(i+u, j+v) 如下圖所示:
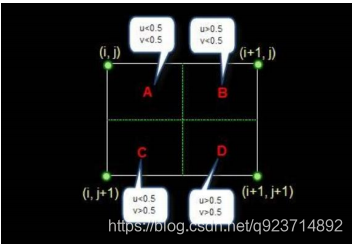
若我們在A區域插入像素,該像素值與(i,j)的值相同,同理若是在B區域插入像素,這該像素值與(i+1,j)的值相同。
缺點:
如果在A區域插入過多的像素,可能造成圖像鋸齒狀。(導致在某一區域的像素值相同,導致失真)
代碼實現:
import cv2
import numpy as np
def function(img):height,width,channels =img.shapeemptyImage=np.zeros((800,800,channels),np.uint8) #建立一個空圖像sh=800/heightsw=800/widthfor i in range(800):for j in range(800):x=int(i/sh)y=int(j/sw)emptyImage[i,j]=img[x,y]return emptyImageimg=cv2.imread("lenna.png")
print(img.shape)
zoom=function(img)
print(zoom.shape)
cv2.imshow("nearest interp",zoom)
cv2.imshow("image",img)
cv2.waitKey(0)
輸出結果:
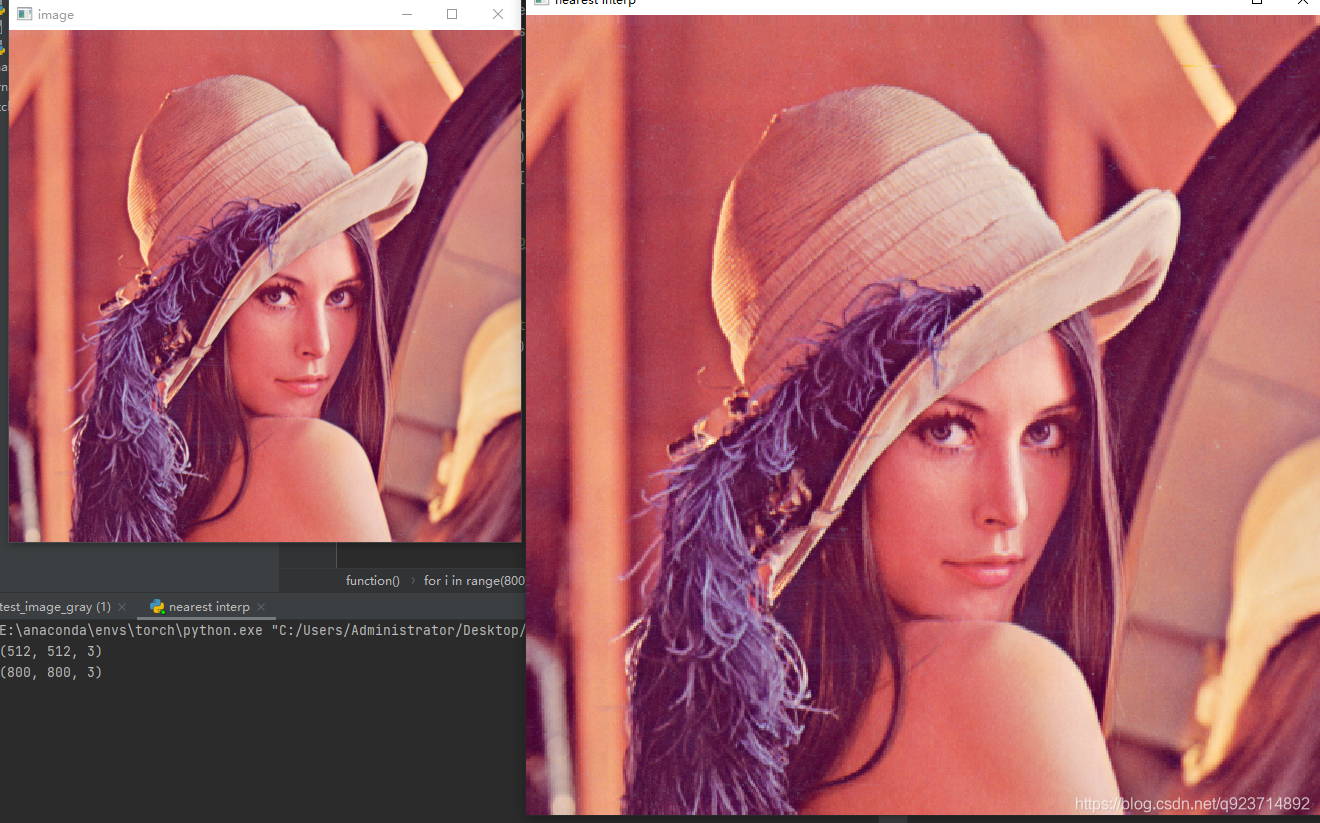
原圖像為512×512,輸出圖像為800×800
二:雙線性插值
公式:
f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)
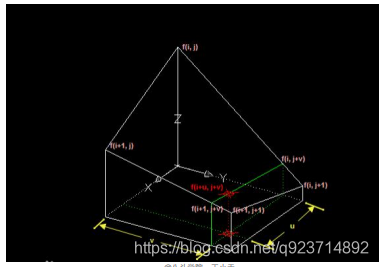
看著有點懵?
我們可以先看看單線性插值:
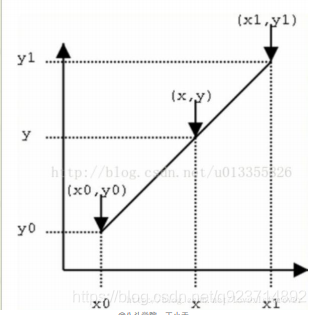
公式:
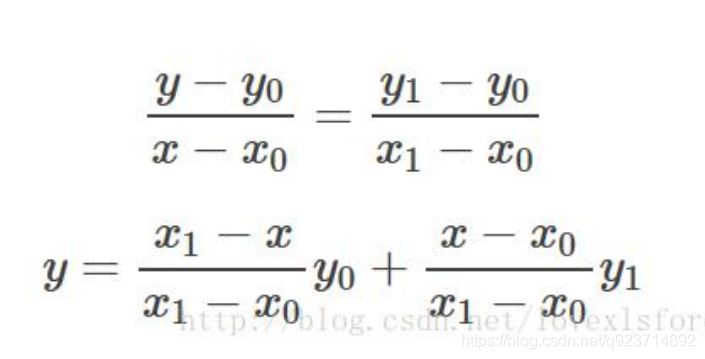
其實就是一個比例關系:我們想要輸入的值是y(像素值),已知的位置點是x(位置)。y和y0的距離差與x和x0的距離差的比值應等于y1和y0的距離差與x1與x0的距離差的比值。從而推導出在單線性的情況下,y的推導公式:
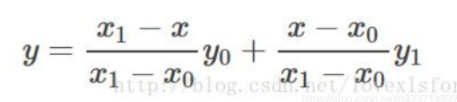
了解了單線性插值,我們推導雙線性插值
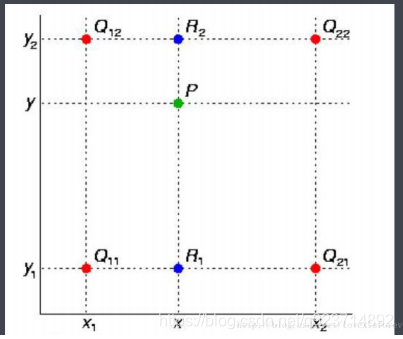
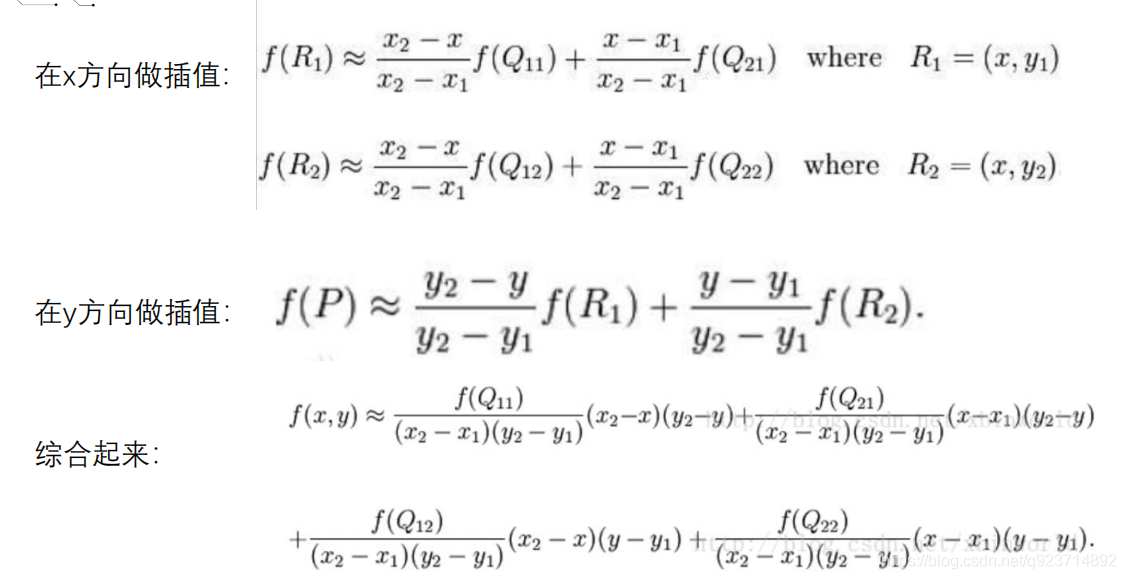
先從x方向做兩次單線性插值,得R1和R2,然后再在y方向做單線性插值:
因為在圖像計算中,x1和x2,y1和y2都是相鄰的點,導致x2-x1=1,y2-y1=1
最后得到的結果其實就是:
f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)
注意:插值算法并不是只能用在放大,在插入像素點的同時,忽略原圖周圍點即為縮小。
雙線性插值有個額外的步驟:中心對齊(能夠對雙向插值的圖像精度的提升)
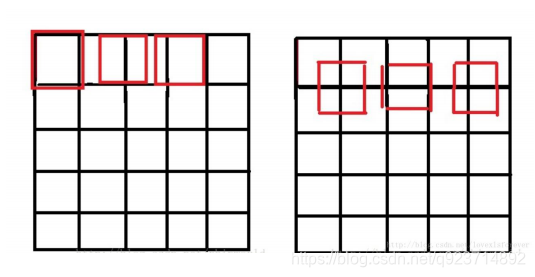
注意:在默認的雙線性插值時,始終以左上角像素點進行對齊,這就導致最右邊的點始終沒有參與插值。可能造成精度損失。
應用中心對齊后的雙線性插值的代碼實現:
import numpy as np
import cv2'''
實現雙線性插值
'''
def bilinear_interpolation(img,out_dim):src_h, src_w, channel = img.shapedst_h, dst_w = out_dim[1], out_dim[0]print ("src_h, src_w = ", src_h, src_w)print ("dst_h, dst_w = ", dst_h, dst_w)if src_h == dst_h and src_w == dst_w:return img.copy()#如果輸入大小與原圖大小相同,則返回原圖dst_img = np.zeros((dst_h,dst_w,3),dtype=np.uint8)#建立一個預輸出的全0圖像scale_x, scale_y = float(src_w) / dst_w, float(src_h) / dst_hfor i in range(3):for dst_y in range(dst_h):for dst_x in range(dst_w):#使用幾何中心對稱#如果使用直接方式,src_x=dst_x*scale_x#scale是比例,通過同比例縮小/放大實現中心對齊src_x = (dst_x + 0.5) * scale_x - 0.5src_y = (dst_y + 0.5) * scale_y - 0.5#找到將用于計算插值的點的坐標src_x0 = int(np.floor(src_x))src_x1 = min(src_x0 + 1 ,src_w - 1)src_y0 = int(np.floor(src_y))src_y1 = min(src_y0 + 1, src_h - 1)# 計算插值temp0 = (src_x1 - src_x) * img[src_y0,src_x0,i] + (src_x - src_x0) * img[src_y0,src_x1,i]temp1 = (src_x1 - src_x) * img[src_y1,src_x0,i] + (src_x - src_x0) * img[src_y1,src_x1,i]dst_img[dst_y,dst_x,i] = int((src_y1 - src_y) * temp0 + (src_y - src_y0) * temp1)return dst_imgif __name__ == '__main__':img = cv2.imread('lenna.png')cv2.imshow('original picture',img)dst = bilinear_interpolation(img,(700,700)) #放大#dst = bilinear_interpolation(img,(200,200)) #縮小cv2.imshow('bilinear interp',dst)cv2.waitKey()輸出結果:
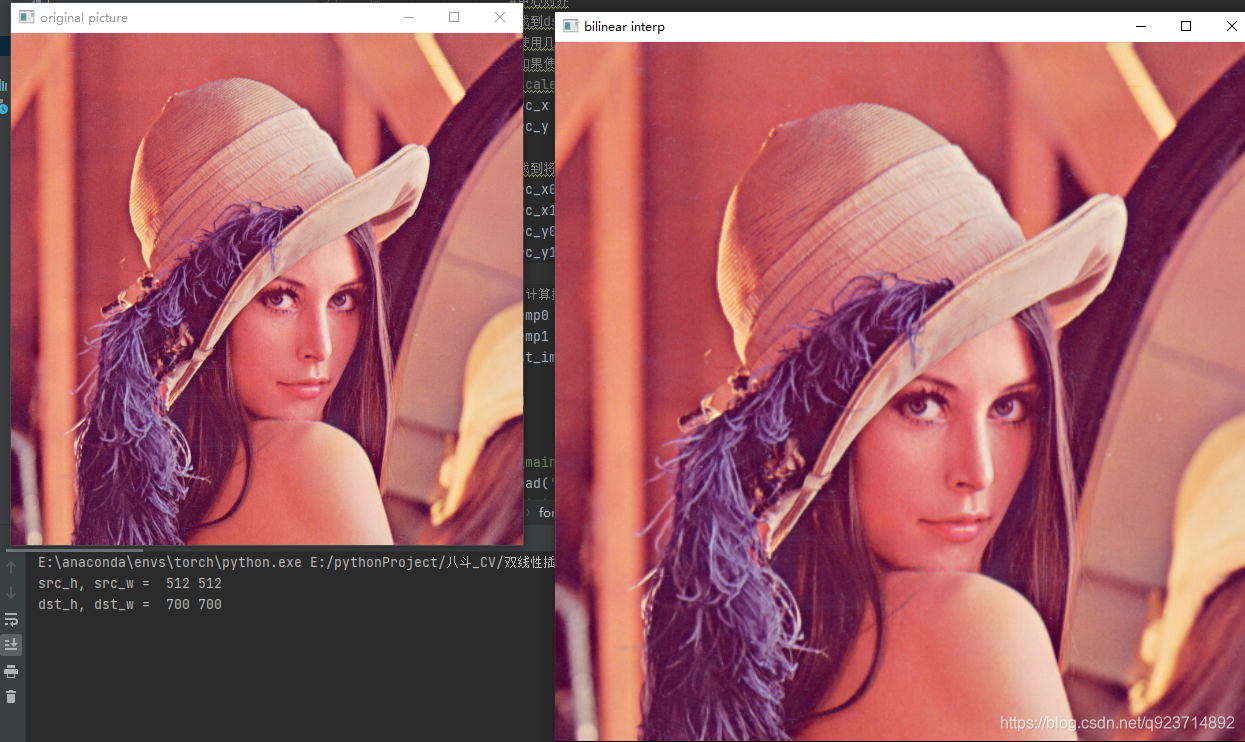
中心對齊代碼解讀:
src_x = (dst_x + 0.5) * scale_x - 0.5
src_y = (dst_y + 0.5) * scale_y - 0.5
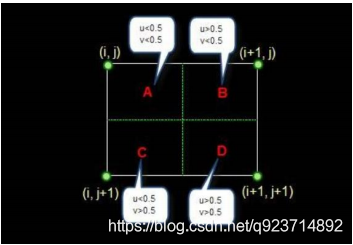
以這個圖為例,可以明顯看出,中心點在(i+0.5,j+0.5),也就是說,先將原圖的中心點找到,然后按照放大/縮小的倍數,最后還需要減去0.5的偏差值。
這里我參考了其他的博客:
將公式變形,srcX=dstX* (srcWidth/dstWidth)+0.5*(srcWidth/dstWidth-1) 相當于我們在原始的浮點坐標上加上了0.5*(srcWidth/dstWidth-1)這樣一個控制因子,這項的符號可正可負,與srcWidth/dstWidth的比值也就是當前插值是擴大還是縮小圖像有關,有什么作用呢?看一個例子:假設源圖像是33,中心點坐標(1,1)目標圖像是99,中心點坐標(4,4),我們在進行插值映射的時候,盡可能希望均勻的用到源圖像的像素信息,最直觀的就是(4,4)映射到(1,1)現在直接計算srcX=4*3/9=1.3333!=1,也就是我們在插值的時候所利用的像素集中在圖像的右下方,而不是均勻分布整個圖像。現在考慮中心點對齊,srcX=(4+0.5)*3/9-0.5=1,剛好滿足我們的要求.




)
填充與Vaild(有效)填充)


)










