In the last post, we saw how actual algorithms are developed and tested. In this post, we will figure out the level of exposure so that can always protect our investments from significant downturns. And find the best performing portfolio given several assets.

在上一篇文章中，我們看到了如何開發和測試實際算法。 在這篇文章中，我們將弄清風險敞口水平，從而始終可以保護我們的投資免受重大衰退的影響。 并根據幾種資產找到表現最佳的投資組合。

Why quantify the risk?

為什么要量化風險？

To invest or trade with confidence. Knowing Value at Risk (VaR) helps us to gauge the potential loss of equity, both in scale and frequency. Not managing this volatility can lead to significant (and avoidable) losses.

有信心地進行投資或交易。 了解風險價值(VaR)幫助我們從規模和頻率上衡量潛在的股權損失。 不控制這種波動會導致重大(和可避免)的損失。

Why Optimize Portfolio?

為什么要優化投資組合？

We are all risk-averse and we want to maximize our profits. Diversification can potentially achieve both of these goals. We can select assets with the best returns that are less correlated with each other. Portfolio return and risk however depend upon final mix or weight allocation to each asset. Not getting allocation right will lead to lower returns/higher risks. We will use mean-variance optimization to find desired weights to construct the best performing portfolio(modern portfolio theory by Markowitz).

我們都規避風險，我們希望最大限度地提高利潤。 多樣化可以潛在地實現這兩個目標。 我們可以選擇相互之間關聯度較低的最佳收益資產。 但是，投資組合的回報和風險取決于最終組合或對每種資產的權重分配。 分配不正確將導致較低的回報/較高的風險。 我們將使用均值方差優化來找到所需的權重，以構建表現最佳的投資組合(Markowitz的現代投資組合理論)。

Short explanation/definition of key terms

簡要解釋/定義關鍵術語

Value at Risk (VaR): Maximum dollar amount (or percentage) expected to be lost over a given time horizon, at a pre-defined confidence/probability level.

風險價值(VaR) ：在給定的時間范圍內，在預定義的置信度/概率水平下，預期損失的最大金額(或百分比)。

Portfolio optimization and efficient frontier: Finding best weights for selected assets such that the expected return is highest for a given risk or vice versa. An efficient frontier is simply a collection of all such dominant/optimized portfolios for all possible risk level.

投資組合優化和有效邊界 ：找到選定資產的最佳權重，以使給定風險的預期收益最高，反之亦然。 有效邊界只是針對所有可能的風險水平的所有此類主導/優化投資組合的集合。

Sharpe ratio: Sharpe ratio is the measure of risk-adjusted return of a portfolio. Degree of excess return beyond risk-free asset for taking extra risk.

夏普比率 ：夏普比率是對投資組合進行風險調整后的收益的度量。 超出無風險資產的超額收益程度，以承擔額外風險。

Capital Market Line (CML): Theoretical concept that gives optimal combinations of a risk-free asset and the market portfolio (portfolio of risky assets).

資本市場線(CML) ：提供無風險資產和市場投資組合(風險資產組合)的最佳組合的理論概念。

Convex optimization: Solving a mean-variance problem as convex functions, here with the help of Solvers.

凸優化 ：在此處借助求解器，將均方差問題解決為凸函數。

Part 1: Value at Risk (VaR)

第1部分：風險價值(VaR)

VaR represents portfolio variance at one extreme (of the distribution). Portfolio risk is calculated as portfolio variance (equivalently standard deviation). Portfolio variance plays a major role in determining the risk characteristic of asset as a whole. Portfolio variance depends upon variance of each asset within the portfolio as well their covariance. Thus when assets are uncorrelated (do not tend to move together) portfolio risks are lower compared to portfolio of assets are highly positively correlated.

VaR代表(分布中)一種極端的投資組合方差。 投資組合風險計算為投資組合方差(等同于標準差)。 投資組合方差在確定整個資產的風險特征中起著重要作用。 投資組合方差取決于投資組合中每個資產的方差及其協方差。 因此，與不高度相關的資產組合相比，當資產不相關(不傾向于一起移動)時，資產組合的風險較低。

For a 2 asset portfolio, portfolio variance is given by following equation where w1, w2 are weights, sigma1, sigma2 are standard deviation of each asset and Cov12 denotes covariance between them.

對于2個資產投資組合，投資組合方差由以下等式給出，其中w1，w2是權重，sigma1，sigma2是每種資產的標準差，Cov12表示它們之間的協方差。

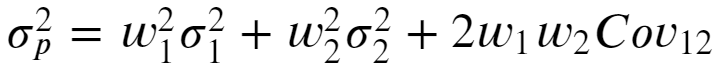
For multiple asset portfolio, position vector and covariance matrix make it much easier to express portfolio variance rather than writing a long summation.

對于多資產投資組合，位置矢量和協方差矩陣使表達投資組合方差比編寫長總和變得容易得多。

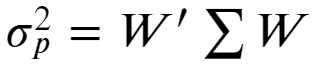
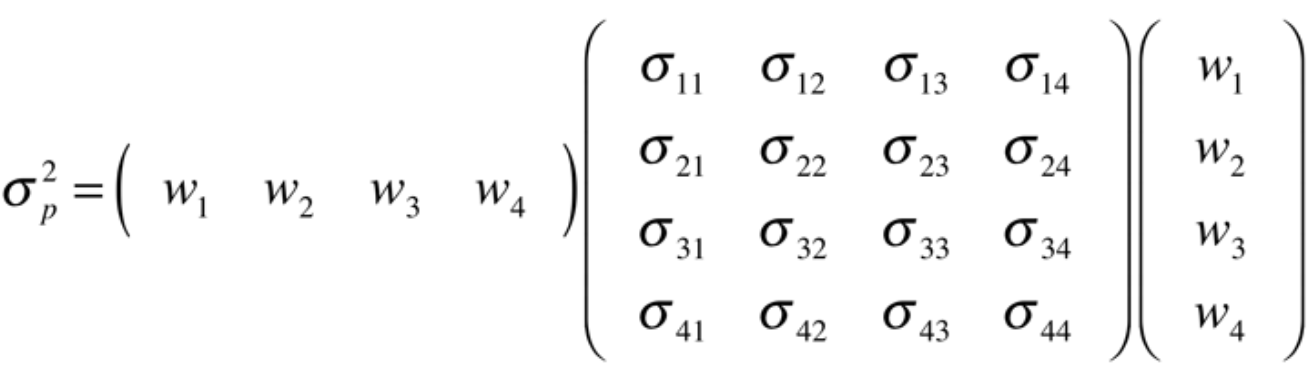
Following is an expanded view of the matrix operation.

以下是矩陣運算的擴展視圖。

With python (Pandas/Numpy or other tools) it is straight forward to calculate the covariance matrix for the whole asset given the series of returns. Matrix multiplication is then used to get portfolio variance.For illustration, I have taken stocks from the Nepal Stock Exchange (NEPSE). 4 highly traded stocks from different sectors were selected. The process involves loading data, calculating return for each stock, computing covariance, and finally calculating portfolio variance as given below.

使用python(Pandas / Numpy或其他工具)，可以很容易地在給定一系列收益的情況下為整個資產計算協方差矩陣。 然后使用矩陣乘法獲得投資組合方差。為說明起見，我從尼泊爾證券交易所(NEPSE)提取了股票。 選擇了4個來自不同行業的高交易量股票。 該過程包括加載數據，計算每只股票的回報，計算協方差，最后計算投資組合方差，如下所示。

While standard deviation tells how much asset can fluctuate every day on average, VaR represents how much asset can fall a single day during a highly volatile period. VaR is expressed as a potential loss of asset (e.g. 4% of the total asset) with a certain probability (e.g. 2% chance or 98% confidence) within a certain time frame (e.g. daily/weekly). Being aware of VaR allows us to keep the right-sized asset or the right mix of assets such that we can avoid unexpected and huge losses.The image below shows that return could be as worse as or worse than -1.64 standard deviation 1 out of 20 trading days (5% probability).

標準差表示平均每天有多少資產波動，而VaR表示在高度波動的時期中一天會有多少資產下跌。 VaR表示為在特定時間范圍(例如每天/每周)內具有一定概率(例如2％機會或98％的置信度)的潛在資產損失(例如總資產的4％)。 意識到VaR可以使我們保留適當大小的資產或正確的資產組合，從而避免出現意外的巨大損失。下圖顯示，收益可能比-1.64標準差1差或更差。 20個交易日(5％的概率)。

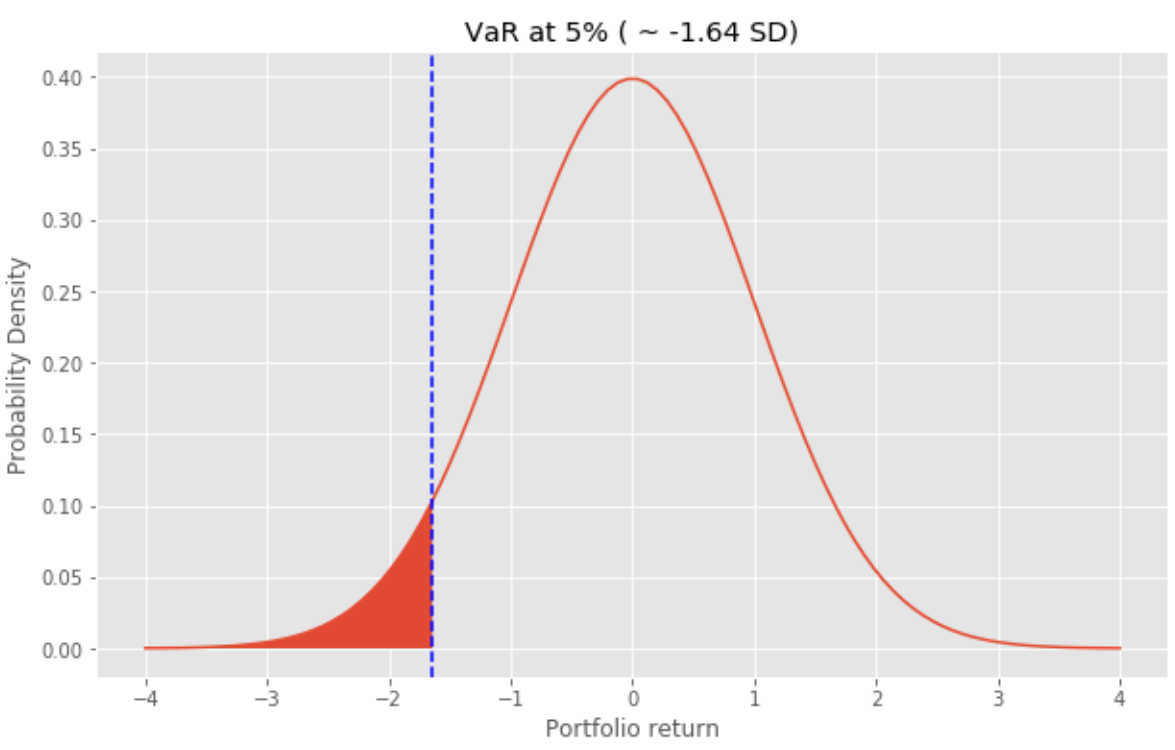
It is obvious that we would want a portfolio and with minimum VaR as possible for any given return. Next, we will find such a portfolio with an optimal combination of weights that has a minimum variance for a specific return. Alternatively, portfolio optimization will help us to maximize our return for any selected risk level.

顯然，我們希望有一個投資組合，并且對于任何給定的回報，都需要盡可能降低VaR。 接下來，我們將找到這樣的投資組合，其權重的最佳組合對于特定收益具有最小的方差。 另外，投資組合優化將幫助我們針對任何選定的風險水平最大化收益。

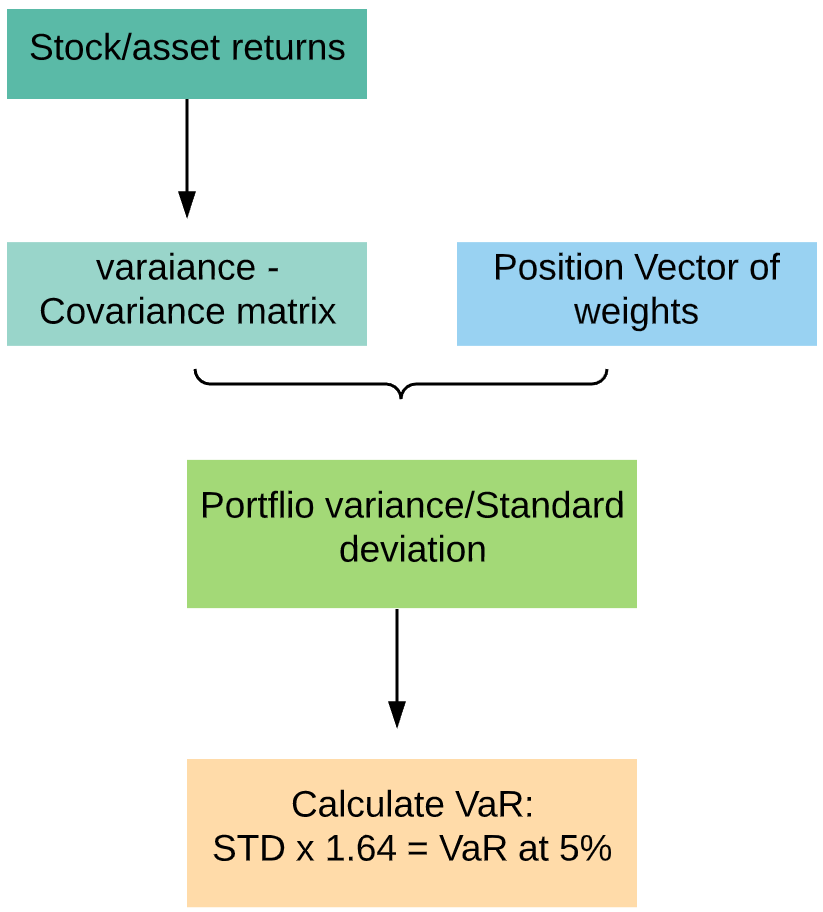
Example: For some random positions(weights) in 4 stocks [0.08, 0.2, 0.58, 0.14] calculated portfolio variance is 0.005, and standard deviation is 0.022 or 2.2% daily std. Assuming a normal distribution of returns, the worst 5% outcomes lie -1.64 SD away from the center. That is returns can be worse than -0.0367 or -3.67% (-1.645*0.022) in 1/20 trading days (5% chance). If we have $100000 invested, our Var at 5% probability is $3670. In other words, we tend to lose $3670 (or more) once in every 20 trading days.

例如：對于4只股票中的一些隨機頭寸(權重)[0.08，0.2，0.58，0.14]，計算出的投資組合方差為0.005，標準差為每日std的0.022或2.2％。 假設收益呈正態分布，則最差的5％收益位于遠離中心的-1.64 SD。 也就是說，在1/20個交易日內(低于5％的機會)回報可能低于-0.0367或-3.67％(-1.645 * 0.022)。 如果我們投資了100000美元，則我們以5％概率出現的Var為3670美元。 換句話說，我們傾向于每20個交易日損失3670美元(或更多)。

Part 2. Portfolio Optimization

第2部分。投資組合優化

We will gradually discover the portfolio we want in few steps. We shall start with completely random allocation (i.e. use random weights). Some of these random weight portfolios have better risk-return trade-off, hence are dominant portfolios. Those lying most upper/outer in the risk-return plot make the efficient frontier. Next, we shall find the Market portfolio by comparing the Sharpe ratio for each random portfolio. Needless to say, the Market portfolio lies on the efficient frontier and has the highest/maximum Sharpe ratio. The line tangent to this point and passing through risk-free asset is the Capital Market Line. The slope and intercept to this line are Sharpe ratio and risk-free rate respectively. Ideally, all investors select their portfolio somewhere on this line depending upon their risk/return preferences.

我們將通過幾個步驟逐步發現我們想要的產品組合。 我們將從完全隨機的分配開始(即使用隨機權重)。 這些隨機權重投資組合中的一些具有更好的風險-收益權衡 ，因此是占主導地位的投資組合 。 那些在風險收益圖上位于最上/最外的人成為有效的前沿 。 接下來，我們將通過比較每個隨機投資組合的夏普比率來找到市場投資組合。 不用說，市場組合位于有效的邊界上，并且具有最高/最大的夏普比率。 與此切線相交并穿過無風險資產的線是資本市場線 。 這條線的斜率和截距分別是夏普比率和無風險利率。 理想情況下，所有投資者都根據風險/回報偏好選擇投資組合。

A. Random allocation of weights: We will visualize the effect of random allocation weights. 1000s of portfolios are taken with random weights, respective mean and variance are calculated (and scattered for visualization). Some combination weight has better risk-return characteristics and therefore are dominating/desirable portfolios.

A.權重的隨機分配：我們將可視化隨機分配權重的效果。 以隨機權重獲取1000個投資組合，計算各自的均值和方差(并分散顯示)。 一些組合權重具有更好的風險收益特性，因此是主導/理想的投資組合。

Portfolio return:

投資組合收益：

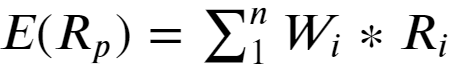
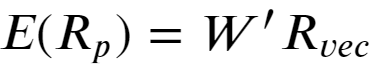
Portfolio risk:

投資組合風險：

B. Market portfolio: Among all possible combinations of dominating portfolios in the efficient frontier, one which gives the highest return for taking additional risk beyond a risk-free rate is designated as a Market portfolio. we can calculate the Sharpe ratio for all portfolios given a risk-free rate and the winning portfolio with the highest Sharpe ratio is the Market Portfolio. All the rational investors gravitate towards to this best performing portfolio.This model of combining risk-free assets with the Market portfolio is known as the Capital asset pricing model (CAPM). All portfolios in CML is optimally compensated for risk above the risk-free rate. Mathematically CAPM is expressed as:

B.市場投資組合：在有效邊界中所有主導投資組合的可能組合中，將承擔無風險利率以外的附加風險獲得最高回報的投資組合指定為市場投資組合。 在無風險利率的情況下，我們可以計算所有投資組合的夏普比率，而夏普比率最高的獲勝投資組合是市場投資組合。 所有理性投資者都傾向于使用這種表現最佳的投資組合。這種將無風險資產與市場投資組合在一起的模型被稱為資本資產定價模型(CAPM)。 CML中的所有投資組合都能獲得高于無風險利率的最佳風險補償。 在數學上，CAPM表示為：

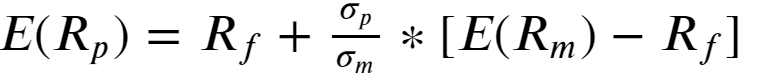
Rearranging, we have Sharpe ratio for combined portfolio :

重新排列后，我們得到了組合資產組合的夏普比率：

Using Rm and Sigma_m calculated from stock return and covariance Sharpe ratio for each random portfolio is calculated, one with the highest Sharpe ratio is the market/optimal portfolio.C. Capital Market Line (CML): Capital Market line represents all combinations of the risk-free asset and the optimal market portfolio. It’s easy to see that the slope of this line is the Sharpe ratio itself and the intercept is a risk-free rate. Given this information, CML can be readily drawn as seen below.

使用從股票收益率和協方差計算得出的Rm和Sigma_m，計算每個隨機投資組合的Sharpe比率，夏普比率最高的是市場/最優投資組合。 資本市場線(CML)：資本市場線代表無風險資產和最佳市場投資組合的所有組合。 不難看出，這條線的斜率就是夏普比率本身，截距是無風險比率。 有了這些信息，就可以很容易地繪制CML，如下所示。

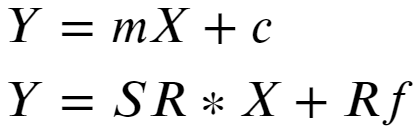
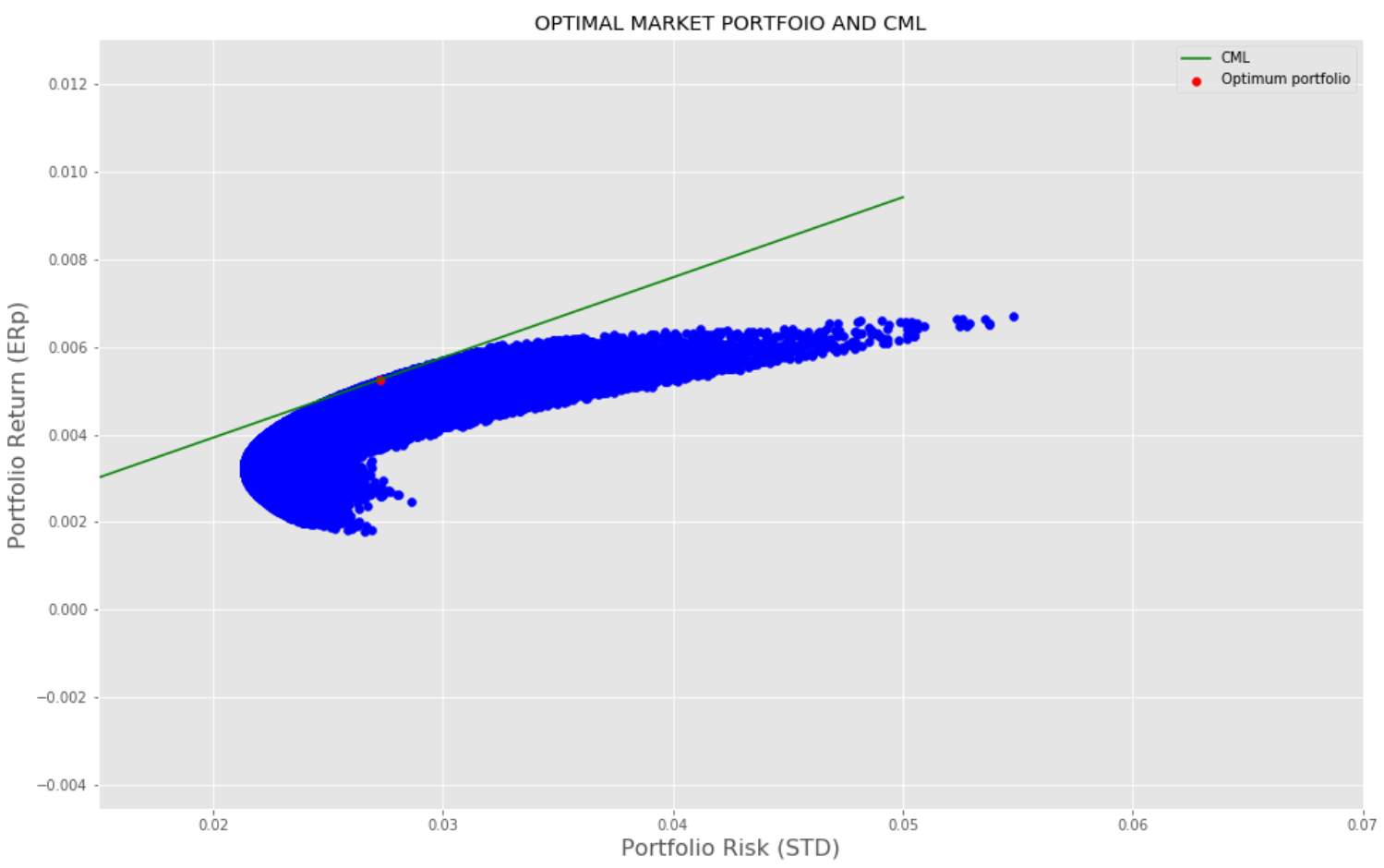
Code for constructing random portfolios, finding a market portfolio, and drawing CML line.

用于構建隨機投資組合，查找市場投資組合和繪制CML線的代碼。

Part 3. Solvers

第3部分。求解器

Random initialization of weights can work for a portfolio with few assets but when assets grow large, the cost of computing and time it takes can be forbidding. However, solving for the best portfolio is an optimization problem with constraints. We can use Solvers from python either for getting single best return (or risk) or get the entire efficient frontier. These are solved as convex problems and the global optimum is always reached.

權重的隨機初始化可以用于資產很少的投資組合，但是當資產變大時，計算成本和花費的時間可能會被禁止。 但是，求解最佳投資組合是具有約束的優化問題。 我們可以使用python的Solvers來獲得單個最佳回報(或風險)或獲取整個有效邊界。 這些問題解決為凸問題，并且始終可以達到全局最優。

The optimization objective is expressed as:

優化目標表示為：

Here weights are represented by x and we are solving for optimal x. Objectives and constraints are written in matrix form. As a rule objective function is stated as a minimization problem. All the inequalities are similarly stated as lesser than some value.

這里的權重用x表示，我們正在求解最優x。 目標和約束以矩陣形式編寫。 通常將目標函數表示為最小化問題。 類似地，所有不平等程度均小于某個值。

Inputs for Solvers:

解算器的輸入：

The algorithm solves for ‘x’ with the help of inputs

該算法借助輸入來求解“ x”

P or quadratic part (here it’s sigma or variance-covariance matrix, cov)

P或二次部分(此處為sigma或方差-協方差矩陣，cov)

q or linear part of the objective function (here represented by a vector of returns r or ER_stocks, above)

q或目標函數的線性部分(此處由上面的收益r或ER_stocks的向量表示)

G and h make the lower bound for weights i.e 0. We can input G as an identity matrix of size n x n (n: number of weights/stocks). Stated as matmul(G, x) < h, hence h is a vector of 0s of size n. while weights are non-negative, while solving they are stated as: -weights < 0.

G和h為權重的下限，即0。我們可以輸入G作為大小為nxn的單位矩陣(n：權重/庫存數)。 表示為matmul(G，x)<h，因此h是大小為n的0s的向量。 權重為非負數，而求解時權重表示為：-weights <0。

A and b make the equality part of the constraint. For our purpose the sum of all weights must equal 1. Hence A is a vector of 1s of size n. matmul(A, r_transpose) = 1, or b is simply 1.

A和b使相等性成為約束的一部分。 為了我們的目的，所有權重的總和必須等于1。因此，A是大小為n的1s的向量。 matmul(A，r_transpose)= 1或b就是1。

We can get the frontier and plot along with random portfolios:

我們可以得到邊界和情節以及隨機投資組合：

Code to solve using Solvers.

使用求解器求解的代碼。

Limitations and Conclusion

局限性和結論

The biggest limitations of this model are the assumption of a normal distribution of returns and the validity of covariance. Actual returns are rarely normal and in fact, highly negative and positive returns are much more common giving rise to so-called fat-tailed distribution. As such the model underestimates the risks. Portfolio variance/risk is very sensitive to variance and covariance pairs i.e. the covariance matrix. Covariance rarely remains the same for a long time, hence finding a robust/valid covariance matrix is challenging.

該模型的最大局限性是假設收益呈正態分布且協方差有效。 實際收益很少是正常的，實際上，高度負收益和正收益更為普遍，從而導致所謂的肥尾分布。 因此，該模型低估了風險。 投資組合方差/風險對方差和協方差對(即協方差矩陣)非常敏感。 協方差很少會長時間保持相同，因此要找到魯棒/有效的協方差矩陣具有挑戰性。

Despite some limitations, risk modeling with VaR is a very helpful and probably most used indicator. Portfolio optimization leads to the most efficient use of our resources and any allocation decisions should be based upon these considerations. Solvers can be used to quickly find the efficient frontier or market portfolio has given return series for each stock.

盡管有一些限制，但使用VaR進行風險建模是一個非常有用且可能是最常用的指標。 投資組合優化可最有效地利用我們的資源，任何分配決策均應基于這些考慮。 解算器可用于快速找到有效的前沿或市場投資組合，從而為每只股票提供收益系列。

You can read the earlier post here:

您可以在此處閱讀之前的文章：