目錄

• • 1、題目
  • 2、思考
  • 3、優化

1、題目

給定一個 沒有重復 數字的序列，返回其所有可能的全排列。

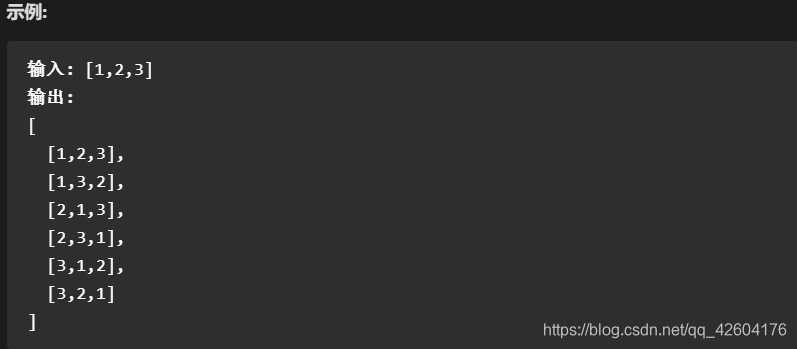
2、思考

老規矩，先畫出給出的例子的解空間樹：

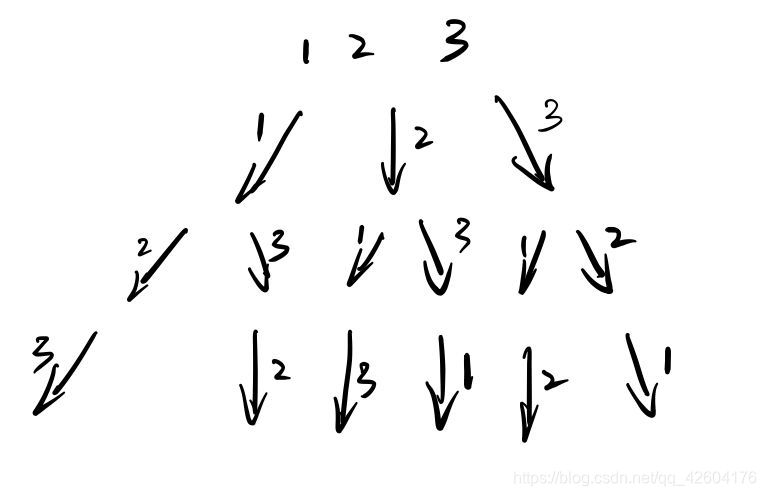
觀察我們可以發現：
1、深度向下一層深入時，出現過的元素不能再出現，我們能選擇的只有沒有選擇過的元素，此處我用的哈希法set。
2、結束條件是：同一個樹枝上的結點個數>=nums數組的size().
于是可以得到初步代碼：注意這里判斷元素是否出現過我用的set，后面會有優化

class Solution {
public:vector<vector<int>> result;vector<int> res;unordered_set<int> set;void backtracking(vector<int>& nums){//如果res元素個數和nums一樣多說明一個排列已經完成if(res.size() == nums.size()){result.push_back(res);return;}for(int i=0;i<nums.size();i++){//如果這個元素在剩下的元素中，處理結點if(set.find(nums[i])!=set.end()){//處理結點；set.erase(nums[i]);res.push_back(nums[i]);//遞歸,探索下一層backtracking(nums);		//遞歸//回溯，撤銷處理結果res.pop_back();set.insert(nums[i]);}//如果這個元素已經用過了，不做處理}return;}vector<vector<int>> permute(vector<int>& nums) {result.clear();res.clear();//裝載setfor(int i=0;i<nums.size();i++)  set.insert(nums[i]);//開始回溯backtracking(nums);return result;}
};

很明顯因為頻繁使用了set的插入操作，刪減操作。我的時間效率并不高。
接下來優化一下。

3、優化

這里判斷是否出現的內容其實就是nums數組的元素。所以我們可以創建一個used數組，對應這個nums數組。
used[i]一開始為false，如果在res中壓入了nums[i]，那么我們就說明這個數用過了。這時使used[i]=true；
再次遍歷的時候，如果used[i]=true；就跳過，說明這個數已經用過了。
下面是優化代碼;

class Solution {
public:vector<vector<int>> result;vector<int> res;vector<bool> used;void backtracking(vector<int>& nums){//如果res元素個數和nums一樣多說明一個排列已經完成if(res.size() == nums.size()){result.push_back(res);return;}for(int i=0;i<nums.size();i++){//如果這個元素在剩下的元素中，處理結點if(used[i] == false){//處理結點；used[i]=true;res.push_back(nums[i]);//遞歸,探索下一層backtracking(nums);		//遞歸//回溯，撤銷處理結果res.pop_back();used[i]=false;}//如果這個元素已經用過了，不做處理}return;}vector<vector<int>> permute(vector<int>& nums) {result.clear();res.clear();//裝載used數組for(int i=0;i<nums.size();i++)  used.push_back(false);backtracking(nums);return result;}
};

對比速度：

有很明顯的速度提升。