兩套學習資料都類似，可參考聚類算法實戰
一、聚類
聚類：物以類聚，人以群分，是無監督學習中的一種。
沒有y，只有x，把不同的x根據相似度自動的聚成好多堆兒
本質上，N個樣本，映射到K個簇中，每個簇中至少含有一個樣本，一個樣本只屬于一個簇
最基本：先給定一個初始劃分，迭代改變樣本和簇的隸屬關系，每次都比前一次好
二、相似度用于場景
Ⅰ，系統推薦
兩點在二維空間距離公式：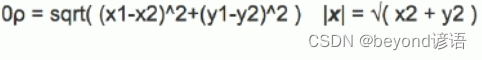
兩點在三維空間距離公式：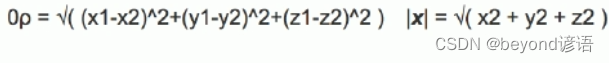
閔可夫斯基距離公式：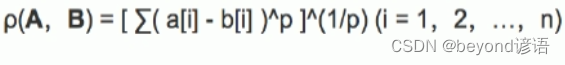
當p=2時，即為歐氏距離；當p=1時，即為曼哈頓距離(Block Distance)；當p趨近于∞，即為切比雪夫距離。
Jaccard similarity coefficient，用于比較有限樣本集之間的相似性與差異性
Jaccard系數值越大，樣本相似度越高
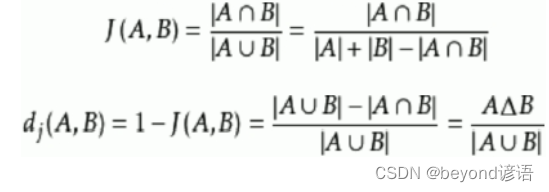
例如：狗蛋兒喜歡1，2，3，4，5
系統給狗蛋兒推薦方案①[1,2,3,6,7,8]，方案②[1,2,3]
這兩個方案按個推薦的效果好？此時就可以通過Jaccard相似系數來進行比較
方案①：3/8、方案②：3/5
故方案②效果更佳
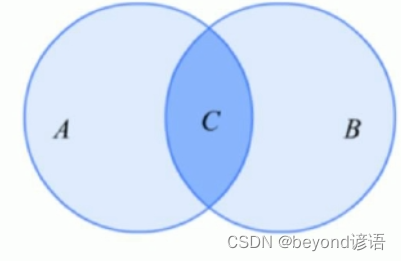
集合A和集合B相交越多，它的相似性越強，當然要考慮它們并在一起的大小，因為集合越大越可能相交的越多，這就有了Jaccard相似系數
可以度量集合，考慮熱門商品
空間嵌入點的問題，有時會用歐式距離，有時會用余弦距離，度量文檔相似性
Ⅱ，網頁去重、防考試作弊、論文抄襲檢查等
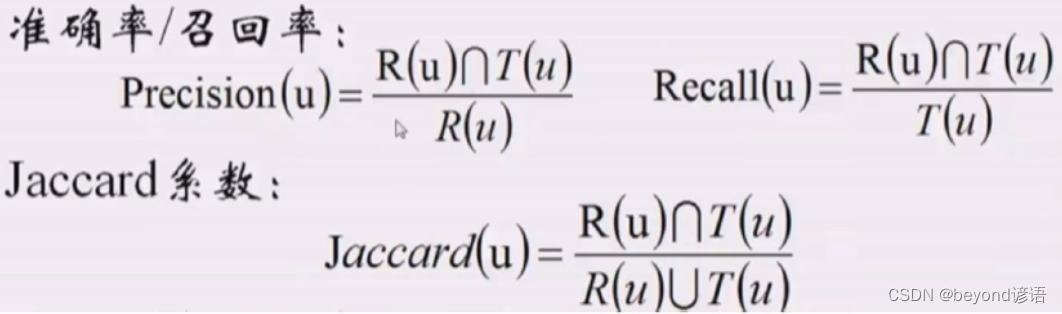
Ⅲ，余弦相似度
余弦距離，余弦相似度
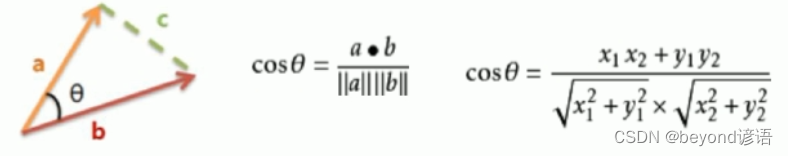
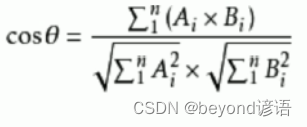
余弦值的范圍在[-1,1]之間，值越趨近于1，代表兩個向量的方向越接近；越趨近于-1，他們的方向越相反；越趨近于0，這兩個向量幾乎正交
最常見的應用是計算文本相似度，將兩個文本根據他們的詞，來建立兩個向量，計算這兩個向量的余弦值，就可以知道這兩個文本在統計學方法中他們的相似度情況
文檔相似度測量考慮推薦SimHash
余弦其實就是Jaccard的分母，看重的是相同的部分，如果是歐氏距離，看重的是差異
Ⅳ，Person相關系數(只能測量線性相關性，1為最相似)和相對熵
①Person相關系數
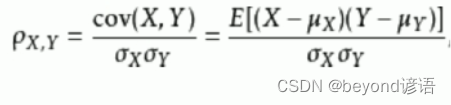
當該公式中的X^和Y ^為零時，就變成了余弦相似度
兩個變量之間的皮爾遜相關系數定義為：兩個變量之間的協方差(分子)和標準差(分母)的商
②相對熵
P和Q相同，相對熵為0
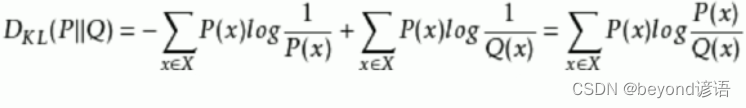
相對熵為交集∩，交叉熵為并集∪
